信息安全复习六:公开密钥密码学
一、章节梗概
1.公开密钥密码模型的基本原理
2.两个算法:RSA&D-H算法
主要内容
1.对称密钥密码的密钥交换问题
2.公钥密码模型的提出
3.设计公钥密码的基本要求
4.数字签名
5.RSA算法
6.公钥密码的特征总结
二、对称密钥密码
对称加密算法中,数据发送方将明文和密钥一起经过特殊加密算法处理成密文后,将它发送出去。接收方收到密文后,若想解读原文,则需要使用加密用到的相同密钥及相同算法的逆算法对密文进行解密,才能使其恢复成原文。
常见的对称加密算法有 AES、DES、Blowfish 等等。
对称加密的核心是只有一把密钥。
对称密钥密码模型中,双方共享的秘密是密钥KEY,解决的问题是保密通道。
对称的、单密钥、秘密密钥、传统密钥:发送方加密和接收方解密使用的是同一个密钥。
该密钥需要事先由发送方和接收方实现共享,是发送方和接收方共同的秘密。
如果密钥泄露,则不安全(无法实现保密性服务)
对称:通信双方是对等的。
三、公开密钥密码模型
非对称加密算法中,有两个密钥:公钥和私钥。它们是一对,如果用公钥进行加密,只有用对应的私钥才能解密;如果用私钥进行加密,只有用对应的公钥才能解密。
非对称加密算法实现机密信息的交换过程为:甲方生成一对密钥并将其中一个作为公钥向其他方公开;得到该公钥的乙方使用该密钥对机密信息进行加密后发送给甲方;甲方再用自己的另一个专用密钥对加密后的信息进行解密。
最有名的非对称加密算法当属 RSA 了,本文将对 RSA 算法的加/解密过程进行详细剖析。
非对称加密拥有两把密钥。
3.1 非对称的、双密钥:每个人都有两个密钥
公钥:公开
私钥:保密
3.2 根据使用的密钥数量区分的两种密码体制
对称的、单密钥、秘密密钥、传统密码技术:发送发和接收方使用同一个密钥。
非对称的、双密钥、公开密码技术:发送方和接收方使用不同的密钥。
加密密钥和解密密钥分割开来,且无法由一个推算出另一个,使得不仅能公开加密算法,公开密钥也可以公开(公告牌、个人主页、号码簿)。
3.3 公开密钥密码
两个密钥:公钥和私钥
非对称:通信双方的地位不平等
往往利用数论的一些函数精心构造
补充而非取代对称密钥密码技术
缺点:公开密钥密码的主要弱点是加解密速度慢。
3.4 公开密钥的历史
1976年Diffie 和 Hellman在论文密码学新方向( New Direction in Cryptography ) 中首次提出了公开密钥密码体制的问题。
Diffie和 Hellman提出了第一个基于公开密钥思想的密码算法,称为D-H算法,此算法可以用于实现密钥交换。
1977年Rivest Shamir和 Adleman三个人实现了公开密钥密码体制,现在称为RSA算法,它是第一个既能用于密钥交换,也能用于数据加密和数字签名的算法。
3.5 公开密钥加密系统
一个公开密钥加密系统由六要素组成:
明文
密文
加密算法
解密算法
公开密钥(PU/KU
私有密钥(PR/KR
3.6公开密钥密码原理总结
公钥:任何人可以知道,用于加密明文或验证签名
私钥:仅有接收者/拥有者知道,用于解密和构造签名。
非对称的含义
密钥的不对称:加/解密密钥不同
用于加密的不能解密,用于解密的不能加密。
双方地位不对等:通信双方知道的秘密不一样多,私钥只能自己知道。
四、数字签名
密钥对互相之间可以交换使用。
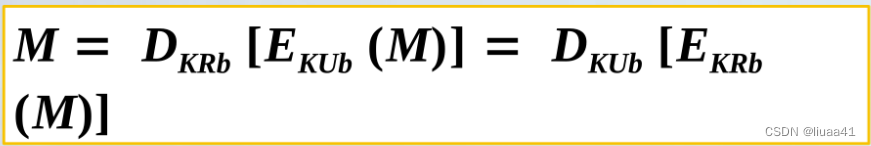
密钥对交换使用能提供什么功能:通信保密、数字签名。
什么是数字签名:所谓数字签名就是一种可以替代手写签名的一种签名技术。
手写签名的安全需求:可认证、抗抵赖。
所谓数字签名就是用私钥加密:可认证、抗抵赖。
对称密钥密码实现不了可认证和抗抵赖的安全需求。
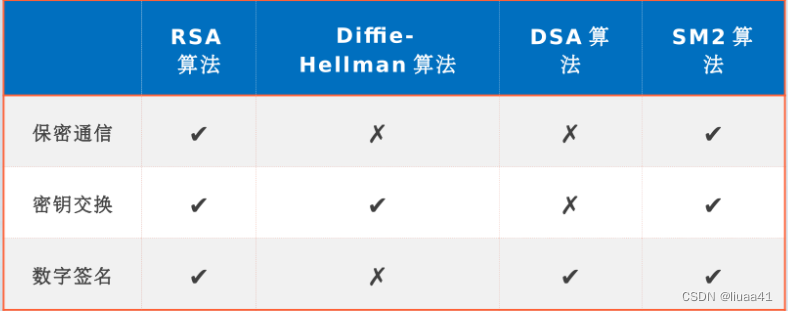
五、RSA算法
5.1 RSA介绍
概念
是一个分组加密算法。
目前被最广泛采用。
基于数论中的Fermat(小)定理实现。
是一个既能用于密钥交换,也能用于数据加密和数字签名的算法。
算法原理
来源于数论的理论基础:要求得两个大素数得乘积很容易,但要分解一个合数为两个大素数得乘积,在计算上几乎不可能;采用得单向函数是大素数相乘,相乘很容易,但因子分解很难。
5.2 RSA密钥生成步骤

5.3 RSA加密和解密
RSA加密

RSA解密

5.4 RSA使用
1.公钥公开:PU={n,e};私钥保密:PR={n,d}
2.加密报文:发送方获取接收方的公钥PU ={n,e}
3.计算密文:C = M^e mod n,0<=M<n
4.解密密文:接收方用自己的私钥PR={n,d}解密
5.计算M = C^d mod n
举例:
选择素数:p=17 & q=11
计算 n = pq = 19× 11 = 187
计算 m = (p-1)(q-1) = 18 × 10 =160
找到 e:gcd(160,e)=1 ,选择 e = 7
计算d:de mod m = 1,7d mod 160 = 1 得 d=23
生成密钥对:公钥PU={187,7};私钥PR={187,23}
RSA加密:M = 88,C = 88^7 mod 187 =11
RSA解密:M = 11^23 mode 187 =88
5.5 RSA的安全性和速度
安全性:破解 RSA 的难点在于对 n 的因数分解,然而大整数的因数分解暂时没有高效的算法。
速度:RSA最快的情况也比DES慢许多倍,无论是软件还是硬件。因此一般只用于少量数据加密,一般做密钥交换。
RSA是最优秀的公钥方案之一。
RSA —— 经典的非对称加密算法
六、公开密钥密码的特征总结
公开密钥算法设计需要有以下基本要求:
加密与解密由不同的密钥完成
知道加密算法,从加密密钥得到解密密钥在计算上是不可行的
两个密钥中的任一个都可以作为加密,而另一个作为解密。
保密通信:公钥加密,私钥解密保密通信
数字签名:私钥加密(签名),公钥解密(验证)
七、公开密钥密码算法的基础
1.单向函数
对于一个函数f(x),如果对于其定义域上的任意x,f(x)都容易计算,同时对子其值域中几乎所有的取值y,计算其逆丽数f^-1(y)都是不可行的,则函数f(x)称为单向函数。
2.可以提供单向函数的三大数学难题
大整数分解问题
离散对数问题
椭圆曲线离散对数问题(简称ECDLP)
3.单向陷门函数
对于一个单向函数f(x),如果其逆函数f^-1(x)在已知某些辅助信息的情况下,容易求解得出,则称该单向函数f(x)称为单向陷门函数。
构造公钥密码系统的关键是如何在求解某个单向函数的逆函数的NP完全问题中设置合理的”陷门”。
4.其它
除RSA算法之外,建立在不同计算难题上的其他公开密钥密码算法有:
基于因子分解问题的Rabin算法;
椭圆曲线公钥算法;
基于有限域中离散对数难题的Elgamal公钥密码算法;
基于“子集和”难题的Merkel-HellmanKnapsack (背包)公钥密码算法;
八、Diffie-Hellman密钥交换算法
8.1 概念
是第一个公钥方案。
使用在一些常用安全协议或产品(例如sSH 、IPSEC)。
8.2 密钥交换方案
不能直接用于有大量数据传输的保密通信;
允许两个用户可以安全地建立一个共享的秘密信息,用于后续的通信过程;
该秘密信息仅为两个参与者知道;
算法的安全性依赖于有限域上计算离散对数的问题
8.3 算法流程
Diffie-Hellman算法简介
相关文章:

信息安全复习六:公开密钥密码学
一、章节梗概 1.公开密钥密码模型的基本原理 2.两个算法:RSA&D-H算法 主要内容 1.对称密钥密码的密钥交换问题 2.公钥密码模型的提出 3.设计公钥密码的基本要求 4.数字签名 5.RSA算法 6.公钥密码的特征总结 二、对称密钥密码 对称加密算法中,数据…...

YOLOv8 更换主干网络之 ShuffleNetv2
《ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design》 目前,神经网络架构设计多以计算复杂度的间接度量——FLOPs为指导。然而,直接的度量,如速度,也取决于其他因素,如内存访问成本和平台特性。因此,这项工作建议评估目标平台上的直接度量,而…...

async/await最详细的讲解
一、async 和 await 在干什么 async 是“异步”的简写,而 await 的意思是等待。async 用于申明一个 function 是异步的,而 await 等待某个操作完成。 async/await 是一种编写异步代码的新方法。之前异步代码的方案是回调和 promise。 async/await 像 p…...

学习数据结构第6天(栈的基本概念)
栈的基本概念 栈的定义栈的基本操作栈的存储结构 栈的定义 栈(Stack)是一种基于先进后出(FILO)或者后进先出(LIFO)的数据结构,是一种只允许在一端进行插入和删除操作的特殊线性表。 栈按照先进后出的原则存储数据,先进入的数据被压入栈底,最…...

自动化添加时间戳版本号
自动化添加时间戳版本号 前言一、静态资源二、版本号的来源三. 版本信息的位置四. 添加时间戳版本号1. 手动添加2. 自动化生成 前言 软件开发和发布过程中,版本是个极其重要的因素。大至操作系统,小到功能组件,都会涉及到版本相关的问题。 …...

【C语言】指针进阶[上] (字符、数组指针、指针数组、数组传参和指针传参)
简单不先于复杂,而是在复杂之后。 目录 1. 字符指针 面试题 2. 指针数组 3. 数组指针 3.1 数组指针的定义 3.2 &数组名 VS 数组名 3.3 数组指针的使用 4. 数组参数、指针参数 4.1 一维数组传参 4.2 二维数组传参 4.3 一级指针传参 4.4 二…...

软件测试外包干了4年,感觉废了..
先说一下自己的情况,大专生,18年通过校招进入湖南某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
ai改写句子软件-ai改写
AI免费伪原创:助力网站内容升级 您是否曾经为网站优化而烦恼,无论是内容更新还是SEO优化,都需要大量的时间和精力。但是,您是否知道,现在有一款能够使用AI技术来帮助您完成这些任务,而且还是免费的呢&…...
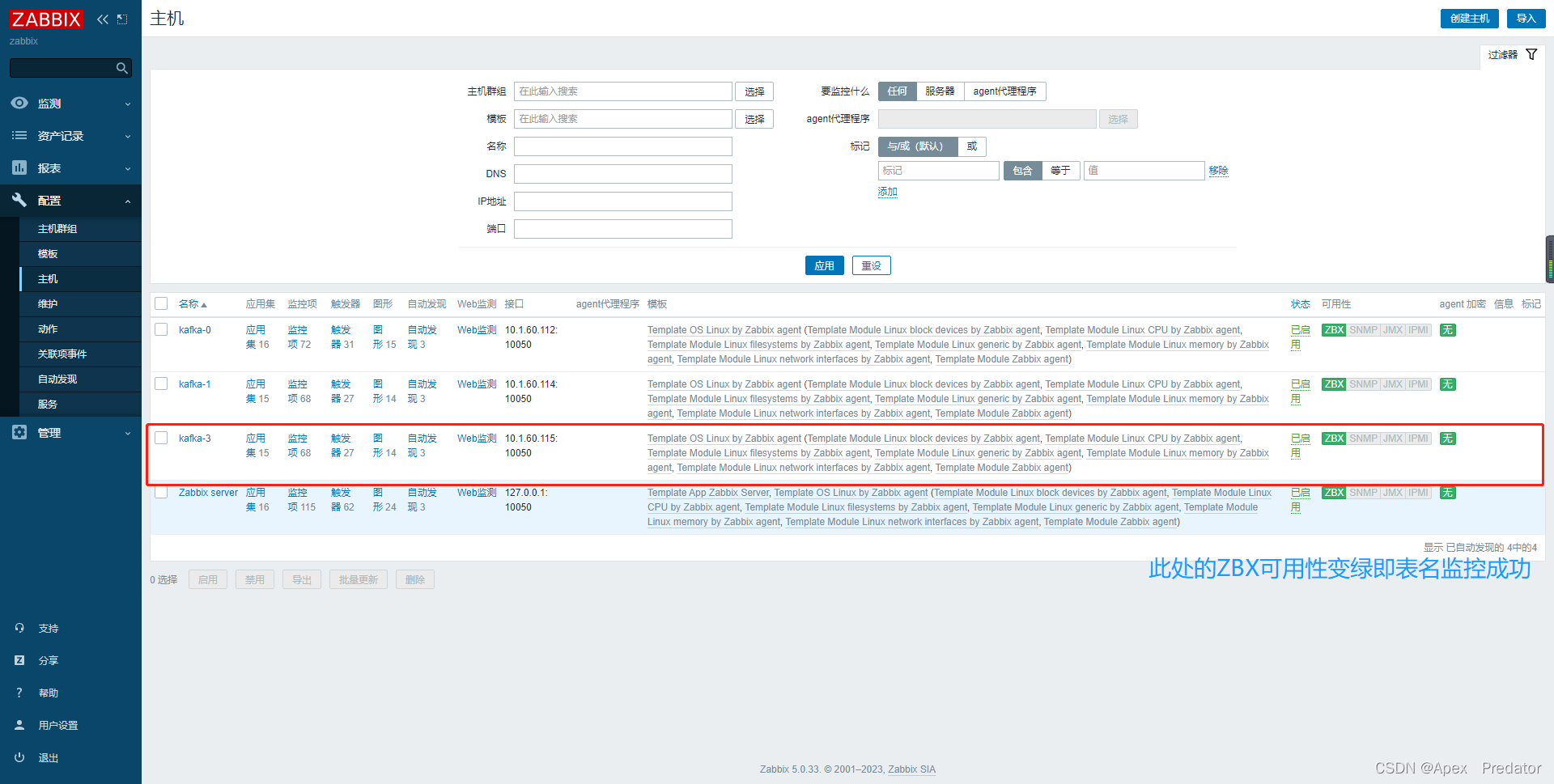
zabbix监控linux主机
1.本实验使用centos7主机,IP地址为10.1.60.115,firewalld和selinux服务已关闭 2.下载zabbix yum源(与zabbix server用一样的版本) rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm 3.安装zabbix客户…...

编程中泛型的使用规则和限制是什么?
泛型是一种程序设计风格,它允许程序员在编写代码时使用一些以后才指定的类型,在实例化时作为参数指明这些类型。泛型主要用于实现通用的数据结构,例如集合、映射、列表等,使得这些数据结构可以存储多种类型的元素。 在泛型使用之…...
【工具】使用VS Code调试Docker Container中的代码
目录 使用VS Code调试Docker Container中的Autoware.ai代码第一种方法 -- 在VS Code中进行DebugStep1Step2Step3Step4c_cpp_properties.jsonlaunch.jsonsettings.jsontask.json Step5Step6Step7参考链接 第二种方法 -- cmake重新编译cmake使用方法(简介)…...

ZVL3网络分析仪
ZVL3 Rohde&Schwarz ZVL3 3G矢量网络分析仪|罗德与施瓦茨 9KHz至3GHz 罗德与施瓦茨Rohde&Schwarz 性能特点: 频率范围 9kHz至3GHz/6 GHz(典型值为5kHz) 测量时间(201个测量点,以校准的双端口) <75ms 数据传输(201个测量点) 在100Mbit/sLAN…...

TCP协议
传输层(协议) TCP协议 三次握手协议保证连接建立 四次挥手,利用这个协议断开连接,而且保证连接通道里面数据已经处理完毕 客户端(Socket): 1、创建客户端的Socket对象(Socket)与指…...

69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1࿱…...

Webshell应急响应指南
Webshell应急响应指南 1.Webshell 排查2.入侵时间确定3.Web日志分析4.漏洞分析5.漏洞复现6.清除Webshell并修复漏洞7.Webshell 防御方法1.Webshell 排查 可利用 Webshell 扫描工具(如 D 盾,河马)对应用部署目录进行扫描,如网站D:\WWW\目录 或者将当前网站目录文件与此前备…...
Linux如何定时执行任务
目录 crontab 介绍 安装crontab 服务操作说明 操作案例 crontab 介绍 Linux crontab是采用定期执行程序的命令,当安装完成操作 系统后,默认便会启动此任务调度命令,crond命令每分钟都会定期检查是否要执行任务的工作,如果要执…...

使用nvm替换nvmw作为nodejs的版本切换(亲测)
之前的文章:同时使用vue2.0和vue3.0版本的采坑记录 安装的nvmw,今天想要用nvmw切换时,居然给我报错了: 然后我就走上了使用nvm替换nvmw之路。。 1.安装 nvm-windows下载 下载release版 中Assets中的包,window10&…...
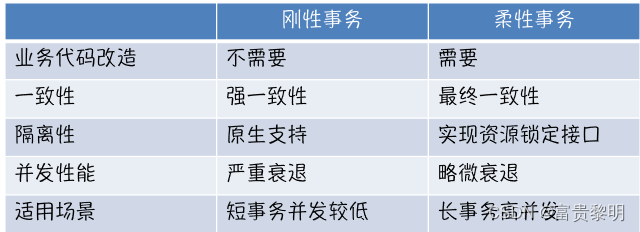
分布式事务
数据库事务 Atomicity 原子性 某个操作,要么全部执行完毕,要么全部回滚 Consistency 一致性 数据库中的数据全都符合现实世界的约束,则这些数据就符合一致性。 比如性别约束男or女,人名币面值不能为负数;出生地址不能…...

zk111111111111111111
Zookeeper 1 zookeeper(作为 dubbo 的注册中心): 概述: zookeper 是 一个分布式的、开源的分布式应用程序的协调服务,管理分布式应 用 作用: 配置管理,分布式锁,集群管理 2 zookeeper 的安装 (dubbo 的资料中已经整理) 3 zookeeper 的数据模型 zookeeper 是一个树形的服…...

018:Mapbox GL加载Google地图(影像瓦片图)
第018个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中加载google地图。 直接复制下面的 vue+mapbox源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共80行)相关API参考:专栏目标示例效果 配置方式 1)查看基础设置:https://xia…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
