5.1 数值微分

学习目标:
作为数值分析的基础内容,我建议你可以采取以下步骤来学习数值微分:
-
掌握微积分基础:数值微分是微积分中的一个分支,需要先掌握微积分基础知识,包括导数、极限、微分等。
-
学习数值微分的概念和方法:了解数值微分的定义、计算方法、误差分析等基础内容,包括前向差分、后向差分、中心差分等常用数值微分方法。
-
理解数值微分的误差和精度:掌握数值微分中误差的来源,包括截断误差、舍入误差等,了解误差的大小和影响因素,以及如何提高数值微分的精度。
-
学习数值微分的应用:数值微分在科学计算中有广泛的应用,如求解微分方程、计算数值积分、图像处理等。学习一些数值微分的应用案例,可以更好地理解数值微分的作用和价值。
-
练习数值微分的计算和编程:通过实践,加深对数值微分的理解和掌握,可以使用计算机编程语言如MATLAB、Python等实现数值微分的算法,并进行计算和比较。
总的来说,学习数值微分需要掌握一定的数学基础,理解数值计算的原理和方法,注重实践和编程能力的提高。

为什么有数值微分:
在实际问题中,有许多函数的解析式难以求得,甚至是无法求得的,而需要求解其导数值,例如在物理、工程、金融等领域的应用中常常需要求解某个函数在某个点处的导数值。由于导数的定义是极限,因此可以通过数值逼近导数值,这就是数值微分的基本思想。另外,有些函数在某些点处的导数不存在,但是可以用数值微分的方法求得近似值,这也是数值微分的应用之一。

5.1.1 利用插值多项式构造数值微分公式
利用插值多项式构造数值微分公式是一种常用的数值微分方法。其主要思想是通过在给定数据点处的函数值构造插值多项式,并利用其导数来逼近函数的导数。最常用的插值多项式是拉格朗日插值多项式,根据插值多项式的导数可得到数值微分公式。
以一阶数值微分为例,假设已知函数 $f(x)$ 在节点 $x_0,x_1$ 处的函数值 $f(x_0),f(x_1)$,则可以通过拉格朗日插值多项式构造出一个一阶数值微分公式。具体地,拉格朗日插值多项式为:
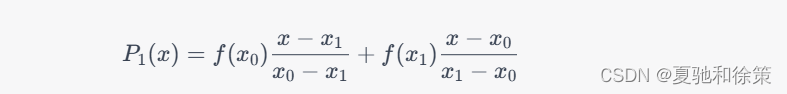
对其求导可得到:
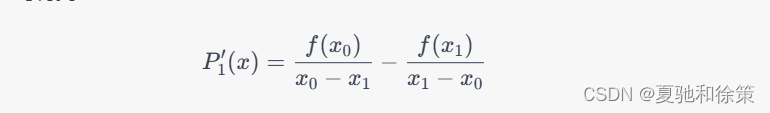
因此,可以将 $P'_1(x)$ 作为 $f'(x)$ 的近似,即
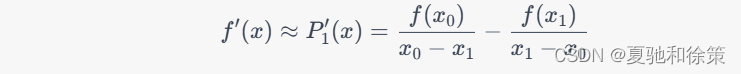
类似地,可以通过二阶拉格朗日插值多项式构造二阶数值微分公式,以此类推。
需要注意的是,插值多项式构造的数值微分公式存在截断误差,即由于采用有限个数据点进行插值,可能会出现插值误差。为了减小截断误差,可以采用更高阶的插值多项式或采用更密集的数据点。此外,还可以通过Richardson外推方法和龙贝格-李布曼算法等数值技巧来进一步提高数值微分的精度。


5.1.2 利用三次样条插值函数构造数值微分公式
利用三次样条插值函数构造数值微分公式的方法叫做三次样条插值微分法。它的主要思想是在每个小区间内,用三次多项式函数来近似替代被积函数,然后再对这些多项式函数进行求导,从而得到数值微分公式。
具体来说,三次样条插值函数的形式为:

其中,a_i,b_i,c_i,d_i是待定系数,x_i\leq x\leq x_{i+1}。
在每个小区间内,由于共有四个未知系数,需要确定四个条件才能唯一确定三次多项式函数,通常选用以下四个条件:
- 插值条件:S(x_i)=f(x_i)$和$S(x_{i+1})=f(x_{i+1})
- 连续性条件:S_i(x_{i+1})=S_{i+1}(x_{i+1})和S_i'(x_{i+1})=S_{i+1}'(x_{i+1})
其中,S_i'(x_{i+1})表示样条函数在x_{i+1}$处的一阶导数,S_i''(x_{i+1})表示样条函数在x_{i+1}处的二阶导数。
通过求解这些条件,可以得到系数a_i,b_i,c_i,d_i,进而得到三次样条插值函数$S(x)$。
接下来,对三次样条插值函数S(x)求导,可以得到数值微分公式,例如:
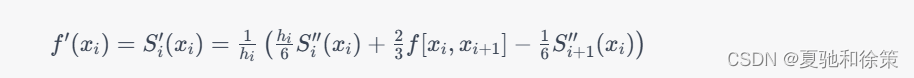
其中,h_i=x_{i+1}-x_i表示小区间的长度,f[x_i,x_{i+1}]表示f(x)在x_i和x_{i+1}处的差商。
总的来说,三次样条插值微分法的优点在于对函数进行了光滑的近似,具有较高的精度和稳定性。

总结:
数值微分的重点、难点和易错点如下:
重点:
- 数值微分是通过数值方法计算导数或高阶导数的一种方法。
- 常见的数值微分方法有差分法、插值法和曲线拟合法。
- 差分法是通过有限差分近似导数的方法,分为前向、后向和中心差分法。
- 插值法是通过利用已知函数值构造插值多项式来计算导数或高阶导数。
- 曲线拟合法是通过拟合曲线的导数或高阶导数来计算数值微分。
难点:
- 数值微分的精度和稳定性受到步长和截断误差的影响,需要进行适当的取舍。
- 差分法需要选择合适的差分格式和步长,过大或过小的步长都会影响精度。
- 插值法需要选择合适的插值点和插值多项式,过拟合或欠拟合都会影响精度。
- 曲线拟合法需要选择合适的拟合曲线类型和拟合点,不同的曲线类型对精度的影响有所不同。
易错点:
- 差分法中心差分法的计算需要注意步长取值和截断误差的影响。
- 插值法需要注意插值点的选择和插值多项式的次数,避免过度拟合或欠拟合。
- 曲线拟合法需要注意拟合点的选择和拟合曲线类型的选取,避免不稳定或过度拟合。
- 在实际应用中,需要根据具体问题选择合适的数值微分方法和参数,进行精度和稳定性的平衡。

相关文章:

5.1 数值微分
学习目标: 作为数值分析的基础内容,我建议你可以采取以下步骤来学习数值微分: 掌握微积分基础:数值微分是微积分中的一个分支,需要先掌握微积分基础知识,包括导数、极限、微分等。 学习数值微分的概念和方…...
云计算服务安全评估办法
云计算服务安全评估办法 2019-07-22 14:46 来源: 网信办网站【字体:大 中 小】打印 国家互联网信息办公室 国家发展和改革委员会 工业和信息化部 财政部关于发布《云计算服务安全评估办法》的公告 2019年 第2号 为提高党政机关、关键信息基础设施运营者…...
laravel5.6.* + vue2 创建后台
本地已经安装好了composer 1.新建 Laravel5.6.*项目 composer create-project --prefer-dist laravel/laravel laravel5vue2demo 5.6.* 2. cd laravel5vue2demo 3. npm install /routes/web.php 路由文件中, 修改 Route::get(/, function () {return view(index); });新建…...
Python自动化sql注入:布尔盲注
在sql注入时,使用python脚本可以大大提高注入效率,这里演示一下编写python脚本实现布尔盲注的基本流程: 演示靶场:sqli-labs 布尔盲注 特点:没有回显没有报错,但根据sql语句正常与否返回不同结果&#x…...

Microsoft Defender for Office 365部署方案
目录 前言 一、Microsoft Defender for Office 365 部署架构 1、部署环境 2、Microsoft Defender for Office 365 核心服务...

字节岗位薪酬体系曝光,看完感叹:不服真不行
曾经的互联网是PC的时代,随着智能手机的普及,移动互联网开始飞速崛起。而字节跳动抓住了这波机遇,2015年,字节跳动全面加码短视频,从那以后,抖音成为了字节跳动用户、收入和估值的最大增长引擎。 自从字节…...

华为OD机试-高性能AI处理器-2022Q4 A卷-Py/Java/JS
某公司研发了一款高性能AI处理器。每台物理设备具备8颗AI处理器,编号分别为0、1、2、3、4、5、6、7。 编号0-3的处理器处于同一个链路中,编号4-7的处理器处于另外一个链路中,不同链路中的处理器不能通信。 现给定服务器可用的处理器编号数组…...
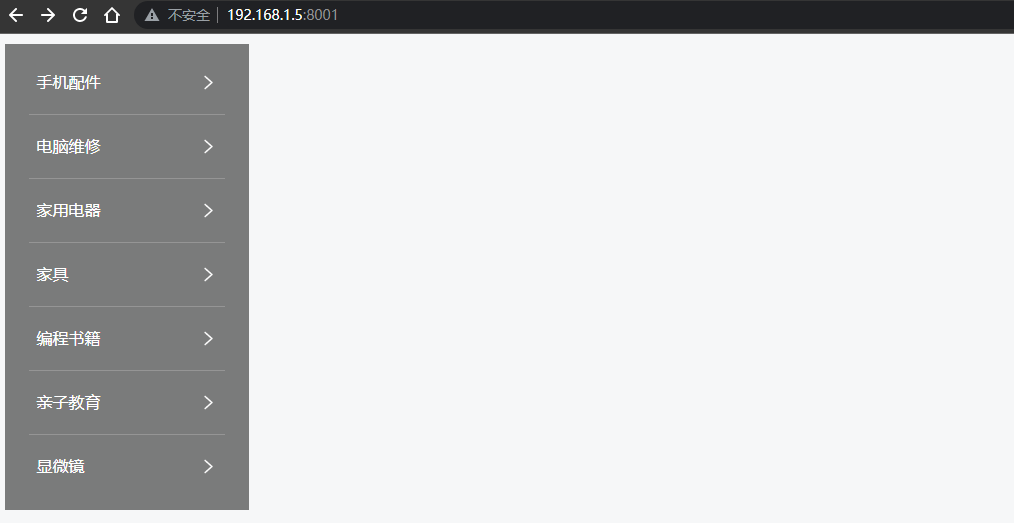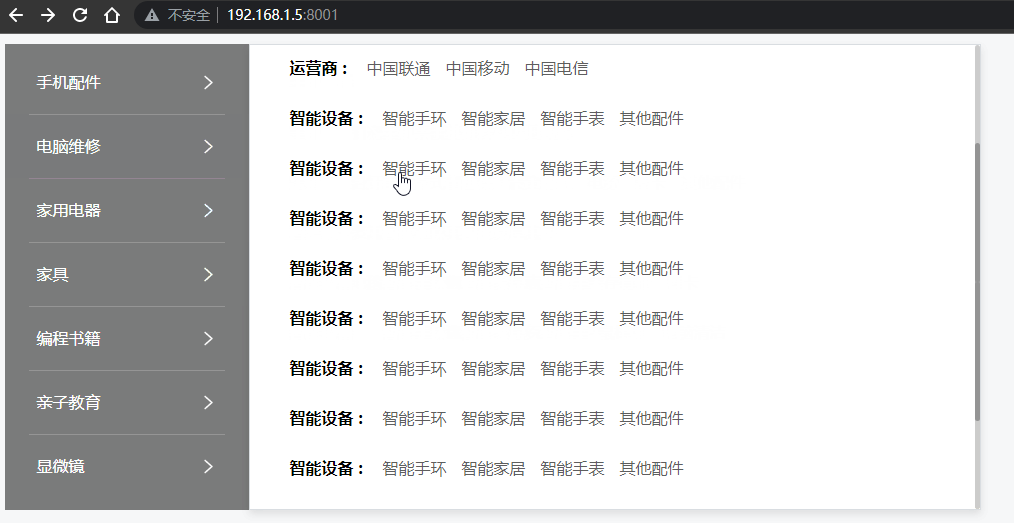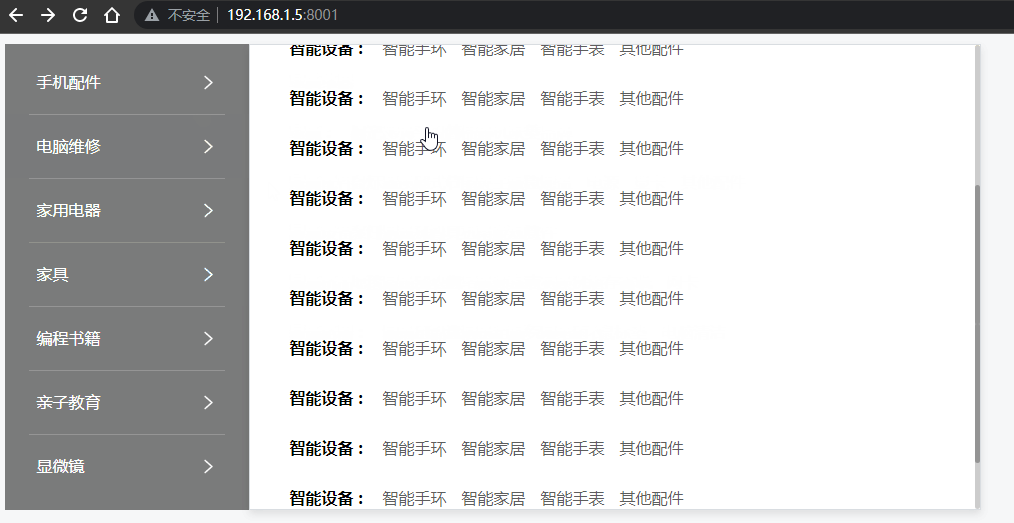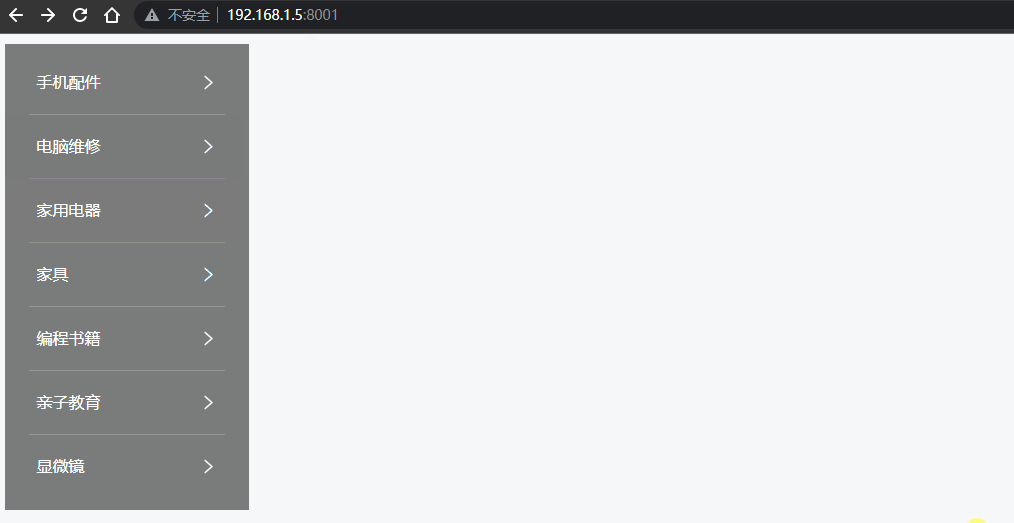
Vue - 实现垂直菜单分类栏目,鼠标移入后右侧出现悬浮二级菜单容器效果(完整示例源码,详细代码注释,一键复制开箱即用)
前言 网上的教程都太乱了,各种杂乱无注释代码、图片资源丢失、一堆样式代码,根本无法改造后应用到自己的项目中。 本文实现了 在 Vue / Nuxt 项目中,垂直分类菜单项,当用户鼠标移入菜单后,右侧自动出现二级分类悬浮容器盒子效果, 您可以直接复制源码,然后按照您的需求再…...
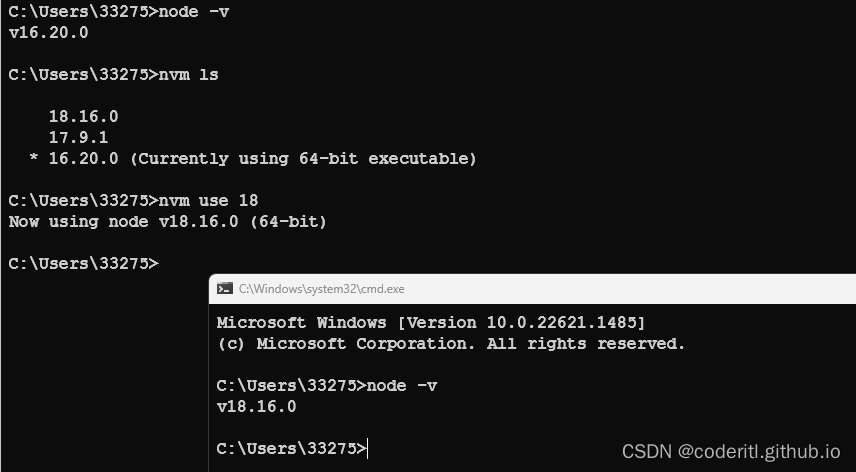
NVM-无缝切换Node版本
NVM-无缝切换Node版本 如果未使用nvm之前已经下载了node,并且配置了环境变量,那么此时删除这些配置(Node的环境以及Node软件),使用nvm是为了在某些项目中使用低版本的node NVM下载 进入github的nvm readme: https://github.com/coreybutler/nvm-windows…...

CCF-CSP真题《202303-1 田地丈量》思路+python,c++满分题解
想查看其他题的真题及题解的同学可以前往查看:CCF-CSP真题附题解大全 试题编号:202303-1试题名称:田地丈量时间限制:1.0s内存限制:512.0MB问题描述: 问题描述 西西艾弗岛上散落着 n 块田地。每块田地可视为…...

Autosar-软件架构
文章目录 一、Autosar软件架构分层图二、应用层三、RTE层四、BSW层1、微控制器抽象层2、ECU抽象层I/O硬件抽象COM硬件抽象Memory硬件抽象Onboard Device Abstraction3、复杂驱动层4、服务层系统服务通信服务CAN一、Autosar软件架构分层图 架构分层是实现软硬件分离的关键,它也…...

8年测开年薪30W,为什么从开发转型为测试?谈谈这些年的心路历程……
谈谈我的以前,从毕业以来从事过两个多月的Oracle开发后转型为软件测试,到现在已近过去8年成长为一个测试开发工程师,总结一下之间的心路历程,希望能给徘徊在开发和测试之前的同学一点小小参考。 一、测试之路伏笔 上学偷懒&#…...
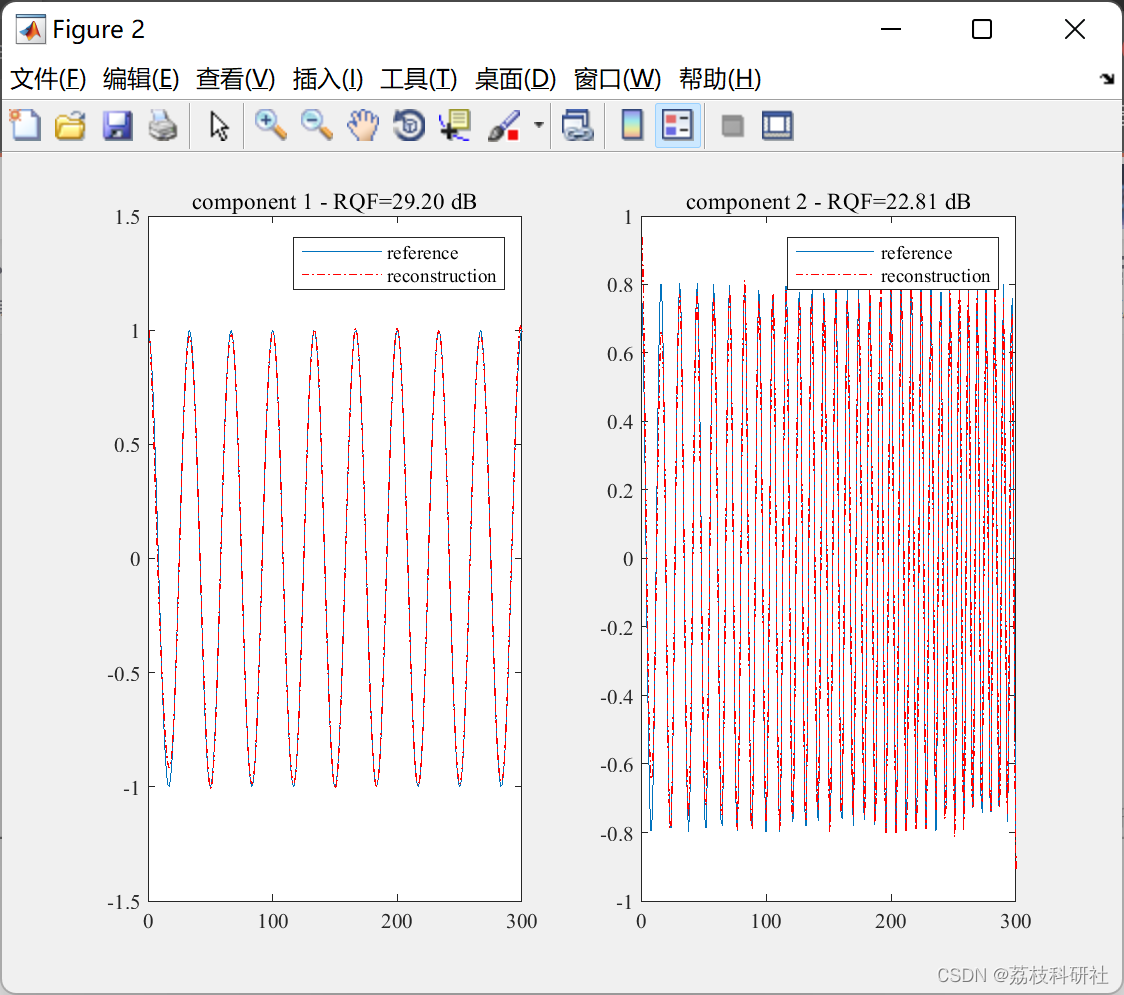
滑动奇异频谱分析:数据驱动的非平稳信号分解工具(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

updateByPrimaryKey和updateByPrimaryKeySelective的区别
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl MyBatis Generator概述 MyBatis Generator是一个专门为MyBatis框架使用者定制的代码生成器,它可以快速的根据表生成对应的映射文件、接口文件、POJO。而且&#…...

【ARM Coresight 4 - Rom Table 介紹】
文章目录 1.1 ROM Table1.1.1 Entry 寄存器 1.2 ROM Table 例子 1.1 ROM Table 在一个SoC中,有多个Coresight 组件,但是软件怎么去识别这些 Coresight 组件,去获取这些Coresight 组件的信息了?这个时候,就需要靠 Core…...

11111111
单选题 1、某地上2层的仪表装配厂房,耐火等级二级,每层建筑面积10000m2,该厂 房二层设有800m2的金属零件抛光工段,采用耐火极限为2.00h的防火隔墙与其他区域分隔,该厂房的火灾危险性为( )。 正确答案:B A.甲类 B.乙类 C.丙…...
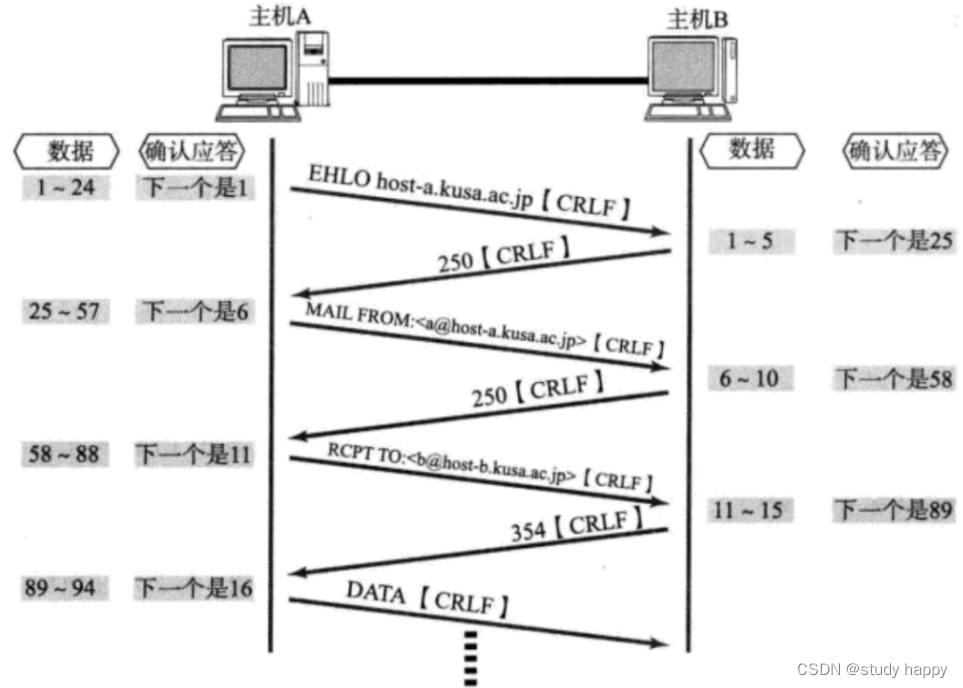
JavaWeb——TCP协议的相关特性
目录 一、TCP 1、特性 2、确认应答 (1)、定义 (2)、原理 (3)、接收缓冲区 3、超时重传 (1)、丢包 (2)、定义 (3)、分类 二、…...

数据结构(C语言实现)——二叉树的概念及二叉树顺序结构和链式结构的实现(堆排序+TOP-K问题+链式二叉树相关操作)
文章目录 1. 前言2. 树的概念及结构2.1 树的概念2.2 树的相关概念2.3 树的表示 3. 二叉树的概念3.1 特殊二叉树3.2 二叉树的性质 4. 二叉树的顺序存储4.1 堆的概念4.2 堆的实现4.2.1 堆的结点定义4.2.2 堆的打印和销毁4.2.3 堆的插入4.2.4 堆的删除4.2.5 取堆顶数据4.2.6 堆的判…...
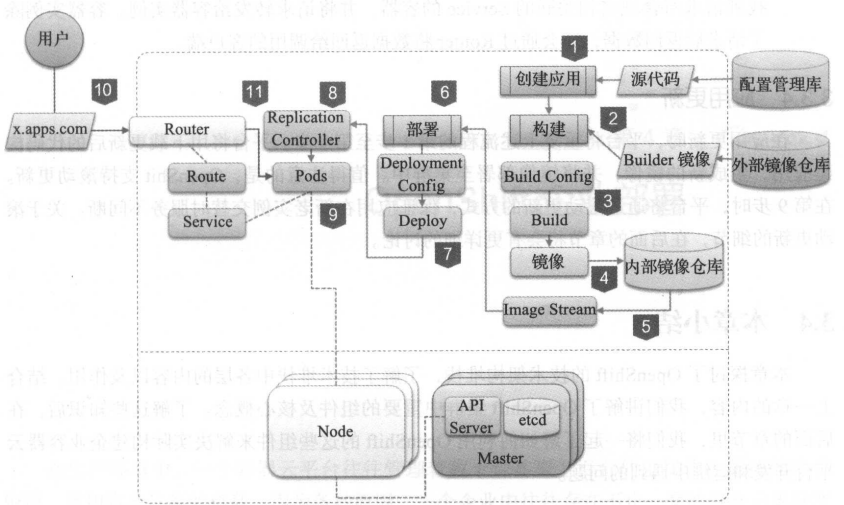
OpenShift:关于OpenShift(OKD)通过命令行的方式部署镜像以及S2I流程Demo
写在前面 因为参加考试,会陆续分享一些 OpenShift 的笔记博文内容为安装完 OpenShift, 利用 OpenShift 引擎部署一个镜像应用和一个 S2I 流程部署应用 Demo学习环境为 openshift v3 的版本,有些旧这里如果专门学习 openshift ,建议学习 v4 版…...
【文字破译原理:信息的相关性】)
楔形文字的破解(钉子形文字)【文字破译原理:信息的相关性】
文章目录 引言I 破解楔形文字1.1 贝希斯敦铭文1.2 破解古波斯楔形文字1.3 破解新埃兰楔形文字和巴比伦楔形文字1.4 破解苏美尔楔形文字引言 祖先借助外力走出了非洲,开始了农耕定居的生活,创造能量的水平和能量的使用效率都越来越高;依靠着语言、文字和书写系统,经验、技术…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
