python数据结构与算法-动态规划(最长公共子序列)
一、最长公共子序列问题
1、问题概念
一个序列的子序列是在该序列中删去若干元素后得 到的序列。
例如:"ABCD”和“BDF”都是“ABCDEFG”的子序列。
最长公共子序列(LCS) 问题: 给定两个序列X和Y,求X和Y长度最大的公共子字列。
例:X="ABBCBDE”Y="DBBCDB”LCS(XY)="BBCD"
应用场景:字符串相似度比对
2、问题求解思路
(1)问题思考
思考: 暴力穷举法的时间复杂度是多少?
序列中的每一个值都有两种选择,被选择或者不被选择,因此一个长度为n的序列,其子序列为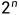 种。求解长度为n和长度为m的序列的公共子序列,对比
种。求解长度为n和长度为m的序列的公共子序列,对比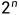 和
和 个子序列之间的关系,是否相同,因此时间复杂度为O(
个子序列之间的关系,是否相同,因此时间复杂度为O( )。
)。
思考: 最长公共子序列是否具有最优子结构性质?
有,见解最优子结构
(2)最优子结构
(LCS的最优子结构):令X=(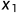 ,
,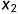 ,......,
,......,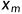 )和Y=(
)和Y=( ,
, ,......,
,......,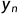 )为两个序列,Z=(
)为两个序列,Z=(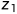 ,
,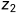 ,......,
,......,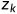 )为X和Y的任意 LCS。
)为X和Y的任意 LCS。
如果
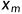 =
= 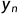 ,则
,则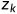 =
= 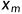 =
= 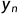 且
且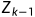 是
是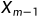 和
和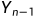 的一个LCS。
的一个LCS。
例如:序列ABCD和ABD,其LCS为ABD,此时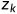 =
= 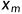 =
= 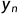 =D,可见,AB是ABC和AB的LCS。
=D,可见,AB是ABC和AB的LCS。
如果
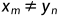 ,且
,且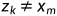 意味着Z是
意味着Z是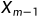 和Y的一个LCS。
和Y的一个LCS。
例如:序列ABCD和ABC,其LCS为ABC,此时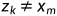 ,即D与C不相等,则
,即D与C不相等,则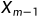 为ABC,可见,ABC是ABC和ABC的LCS。
为ABC,可见,ABC是ABC和ABC的LCS。
如果
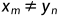 ,且
,且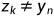 意味着Z是X和
意味着Z是X和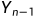 的一个LCS。
的一个LCS。
例如:序列ABC和ACD,其LCS为AC,此时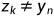 ,即D与C不相等,则
,即D与C不相等,则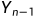 为AC,可见,AC是ABC和AC的LCS。
为AC,可见,AC是ABC和AC的LCS。
示例如下:
要求a="ABCBDAB"与b="BDCABA"的LCS:
由于最后一位"B“≠"A”:
因此LCS(a,b)应该来源于LCS(a[:-1],b)与LCS(a,b[:-1])中更大的那一个
(3)问题递推式
1)递推式推理说明
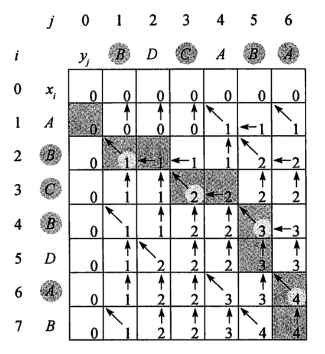
结合最优子结构的定理,可以得到以上的图。
举例解析:
x0都是空列表,y0也是空列表,因此与x0或者y0的LCS一定是0。
序列BDC和序列A:C != A,则LCS来源与LCS([BDC],[ ])和LCS([BD],[A])中,图中可看出,两者都为0,即LCS([BDC], [A])的左边和上边的位置。
序列BDCA和序列A:A = A,则A一定是两个序列的LCS中的一个元素,且LCS([BDC], [A])加上元素A就是LCS([BDCA], [A])。查看可知,LCS([BDC], [A]) = 0,所以LCS([BDCA], [A]) = 0 + 1(元素A)。
剩余的同理。
2)递推式
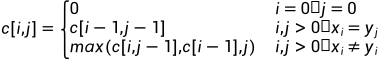
c[i,j]表示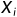 和
和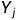 的LCS长度
的LCS长度
二、最长公共子序问题代码实现
1、最长公共子序长度求解
def lcs_length(x,y): # 公共子序列长度,x,y: 字符串、列表等序列m = len(x) # x序列长度n = len(y) # y序列长度c = [[0 for i in range(n + 1)] for _ in range(m+1)] # 创建m行n列二维数组,初始值为0 for i in range(1, m+1): # 按数组的行求,x0都为0不用求,所以从1开始for j in range(1, n+1): # 数组每行中的遍历,y0都为0,不用求if x[i - 1] == y[j - 1]: # x[i-1]其实是字符串的i,因为i=0在二维列表中都是0,不求解,但是在字符串中仍需要从索引0遍历c[i][j] = c[i-1][j-1] + 1 # 递推式else: # xi!=yic[i][j] = max(c[i-1][j],c[i][j-1]) # 递推式return c[m][n] # x和y的最后一个元素对比完,二维数组的最后一位print(lcs_length('ABCBDAB', 'BDCABA'))输出结果
42、最长公共子序的序列求解
动态规划+ 回溯算法搭配使用,动态规划求解最优值,回溯法推算出过程的解。
(1)动态规划求解并存储解-代码实现
# 动态规划求解,存储解及解的计算过程
def lcs(x,y): # 求解并存储箭头方向,x,y为字符串、列表等序列m = len(x) # x的长度n = len(y) # y的长度c = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储长度结果d = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储箭头方向,1表示左上,2表示上,3表示左for i in range(1,m+1): # 按行遍历二维数组for j in range(1,n+1): # 每行的各数值遍历, c0j和ci0相关的值都为0,所以均从1开始if x[i - 1] == y[j - 1]: # xi=yi的情况,二维数组中i,j=0时,都为0已经确定,但字符串x,y仍需从0开始遍历c[i][j] = c[i - 1][j - 1] + 1 # 递推式d[i][j] = 1 # 箭头方向左上方elif c[i][j - 1] > c[i - 1][j]: # 递推式,选择更大的c[i][j] = c[i][j - 1]d[i][j] = 3 # 箭头左边else: # c[i-1][j] >= c[i][j-1]c[i][j] = c[i - 1][j]d[i][j] = 2 # 箭头上方return c[m][n], dc, d = lcs("ABCBDAB", "BDCABA")
for _ in d:print(_)输出结果:
[0, 0, 0, 0, 0, 0, 0]
[0, 2, 2, 2, 1, 3, 1]
[0, 1, 3, 3, 2, 1, 3]
[0, 2, 2, 1, 3, 2, 2]
[0, 1, 2, 2, 2, 1, 3]
[0, 2, 1, 2, 2, 2, 2]
[0, 2, 2, 2, 1, 2, 1]
[0, 1, 2, 2, 2, 1, 2](2)回溯算法的应用-代码实现
# 动态规划求解,存储解及解的计算过程
def lcs(x,y): # 求解并存储箭头方向,x,y为字符串、列表等序列m = len(x) # x的长度n = len(y) # y的长度c = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储长度结果d = [[0 for i in range(n+1)] for _ in range(m+1)] # 二维数组,初始值为0,用于存储箭头方向,1表示左上,2表示上,3表示左for i in range(1,m+1): # 按行遍历二维数组for j in range(1,n+1): # 每行的各数值遍历, c0j和ci0相关的值都为0,所以均从1开始if x[i - 1] == y[j - 1]: # xi=yi的情况,二维数组中i,j=0时,都为0已经确定,但字符串x,y仍需从0开始遍历c[i][j] = c[i - 1][j - 1] + 1 # 递推式d[i][j] = 1 # 箭头方向左上方elif c[i][j - 1] > c[i - 1][j]: # 递推式,选择更大的c[i][j] = c[i][j - 1]d[i][j] = 3 # 箭头左边else: # c[i-1][j] >= c[i][j-1]c[i][j] = c[i - 1][j]d[i][j] = 2 # 箭头上方return c[m][n], d# 回溯算法
def lcs_trackback(x,y): # 最长公共子序列的序列c, d = lcs(x, y) # c长度,d箭头方向i = len(x) # x的长度j = len(y) # y的长度res = [] # 结果列表while i > 0 and j > 0 : # 序列x和y还有值未比对,任何一个序列为0了都不再继续if d[i][j] == 1: # 箭头左上方 ——> 匹配res.append(x[i - 1]) # 二维列表中i=0时,值为0,但是序列x的值是从0开始遍历的i = i - 1 # 位置移到左上位置j = j - 1elif d[i][j] == 2: # 箭头上方->不匹配i = i - 1 # 位置往上移一格else: # dij = 3 ,箭头左向j = j - 1 # 位置往左移一格return "".join(reversed(res)) # 列表翻转,并将列表用''连接成字符串print(lcs_trackback("ABCBDAB", "BDCABA"))结果输出
BCBA相关文章:
python数据结构与算法-动态规划(最长公共子序列)
一、最长公共子序列问题 1、问题概念 一个序列的子序列是在该序列中删去若干元素后得 到的序列。 例如:"ABCD”和“BDF”都是“ABCDEFG”的子序列。 最长公共子序列(LCS) 问题: 给定两个序列X和Y,求X和Y长度最大的公共子字列。 例:X"ABBCBDE”…...

Java版企业电子招投标系统源码 Spring Cloud+Spring Boot 电子招标采购系统功能清单
一、立项管理 1、招标立项申请 功能点:招标类项目立项申请入口,用户可以保存为草稿,提交。 2、非招标立项申请 功能点:非招标立项申请入口、用户可以保存为草稿、提交。 3、采购立项列表 功能点:对草稿进行编辑&#x…...
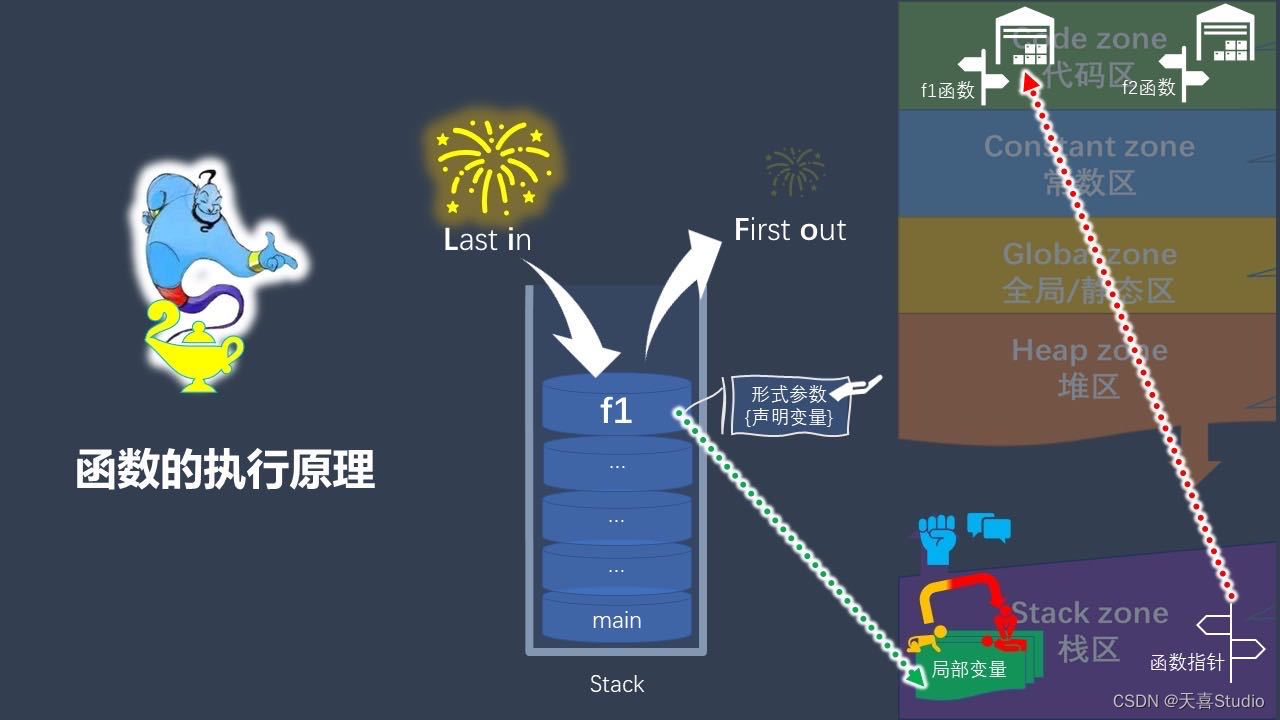
【c语言】函数的基本概念 | 函数堆栈调用原理
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
Vue.prototype 详解及使用
前言: 我们可能会在很多组件里用到数据/实用工具,但是不想污染全局作用域。这种情况下,可以通过在原型上定义它们使其在每个 Vue 的实例中可用。 1. 基本示例 在main.js中添加一个变量到 Vue.prototype Vue.prototype.$appName My App这…...

音视频八股文(3)--ffmpeg常见命令(2)
07-ffplay命令播放媒体 播放本地文件 播放本地 MP4 视频文件 test.mp4 的命令,从第 2 秒位置开始播放,播放时长为 10 秒,并且在窗口标题中显示 “test time”: ffplay -window_title "test time" -ss 2 -t 10 -autoe…...

使用bert4keras出现的问题(Process finished with exit code -1073741819 (0xC0000005))
1、环境 python 3.7.12 tensorflow 1.15 keras 2.3.1 bert4keras 0.9.7 protobuf 3.19.0 numpy 1.16.5 2、出现问题 numpy版本不兼容问题所以你就直接按照我的版本就可以了(numpy 1.16.5) Process finished with exit code -1073741819 (0xC0000005) …...
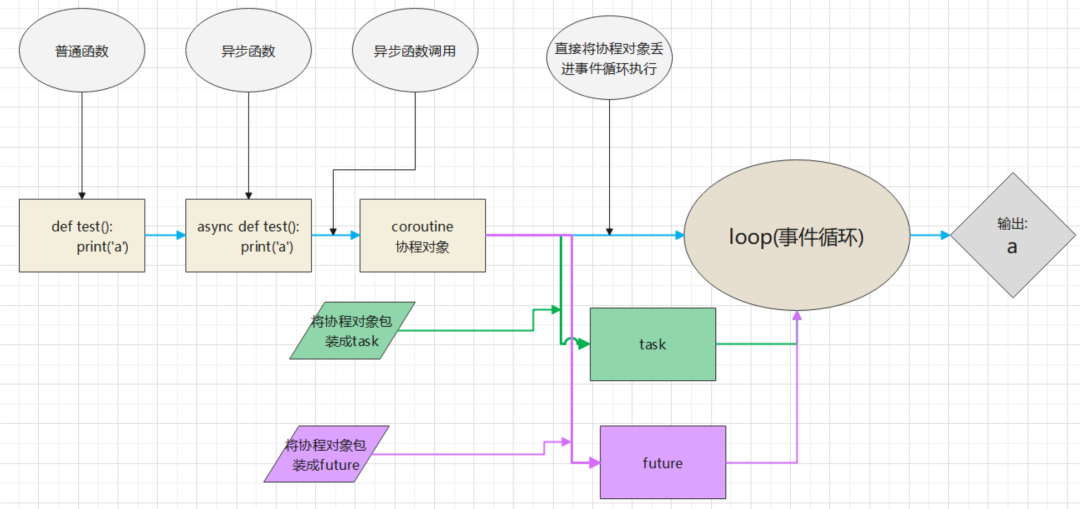
python协程实战
协程简介 协程(Coroutine)又称微线程、纤程,协程不是进程或线程,其执行过程类似于 Python 函数调用,Python 的 asyncio 模块实现的异步IO编程框架中,协程是对使用 async 关键字定义的异步函数的调用; 一个进程包含多个线程,类似…...
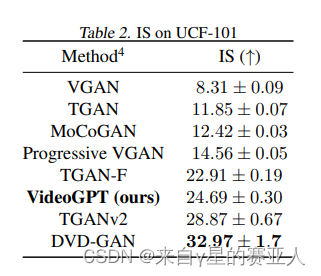
【论文笔记】VideoGPT: Video Generation using VQ-VAE and Transformers
论文标题:VideoGPT: Video Generation using VQ-VAE and Transformers 论文代码:https://wilson1yan. github.io/videogpt/index.html. 论文链接:https://arxiv.org/abs/2104.10157 发表时间: 2021年9月 Abstract 作者提出了…...
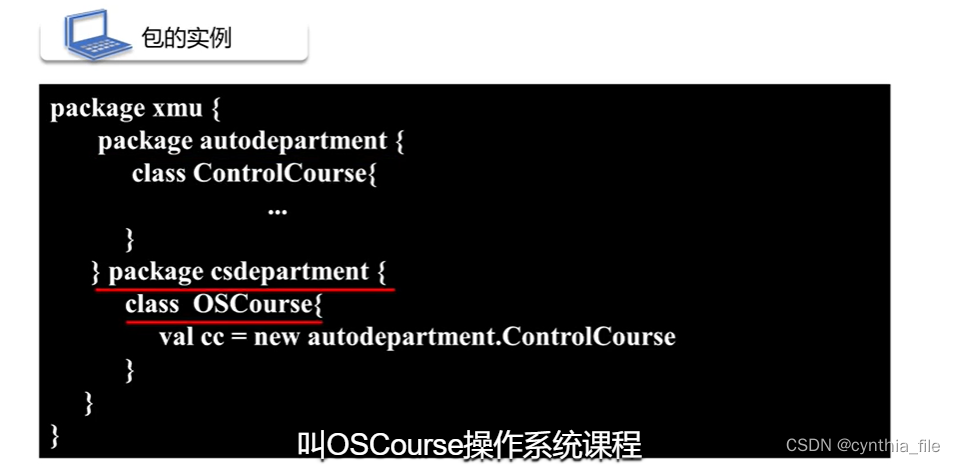
scala之基础面向对象
scala 既是面向对象 也是函数式编程 从Java 发展而来,依赖JVM环境 一、 scala 在linux中运行 scala 模式中直接编写运行 scala文件,load执行 scala编译程序 编译 运行 scala java 二、scala 数据类型 基础数据类型 val 不可变变量 函数式编程 …...

Qt5.12实战之多线程编程概念
1.为什么要使用多线程? a. 基于线程,同时处理多个任务,软件响应更灵敏 b.充分利用CPU的多核心功能增加应用运行效率 c.多线程在同一进程间使用共享通信更加高效 d.多个线程之间进行切换比多个进程之间进行切换,线程开销更少. 2.操作系统与进程关系 a. MS-DOS系统 属于单进程…...
格式化数据恢复怎么做?超实用的3种方法在这!
案例:格式化数据怎么恢复 【我的电脑前段时间中病毒了,无奈之下我只能将其格式化,但是很多重要的文件和图片之类的也一起被删除了,有什么方法可以恢复这些格式化的数据吗?非常着急!】 格式化数据恢复&…...

【Java|golang】1105. 填充书架---动态规划
给定一个数组 books ,其中 books[i] [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。 按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。 先选几本书放在书架上(它们的厚度之和小于等于书架的宽度 shelfWidt…...

linux基础命令
linux基础命令 一、linux命令 熟悉账务linux命令对运维的好处是巨大的,只有熟悉了命令咱们在运维的操作上才能如鱼得水。 系统信息 arch #显示机器的处理器架构(1) uname -m #显示机器的处理器架构(2) uname -r #显示正在使用的内核版本 dmidecode -q …...

【三十天精通Vue 3】 第十八天 Vue 3的国际化详解
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、Vue 3 国际化概述1.1 国际化的概念1.2 国际化的作用1.3 V…...

02 - 学会提问
学会提问 一、引言 1.1 GPT简介 GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的大型预训练语言模型。 凭借其强大的文本生成、理解和处理能力,GPT已在诸如自然语言处理、机器翻译、文本摘要等多个领域取得了显著的…...

Java经典的Main方法面试题
mian方法是做什么用的? main方法是Java程序的入口方法,JVM在运行的时候会首先查找main方法不用main方法如何运行一个类? 不行,没有main方法我们不能运行Java类 在Java7之前,你可以通过使用静态初始化运行Java类。但是&…...

世界大学电子电气工程TOP10,国内大学哪家强?
EE究竟是什么专业 ? 在中国,工程系中跟电相关的专业,一般都切分得非常细。有电子工程、电气工程、通信工程、信息工程、自动化、测控仪器等。但在国外,一般把这些领域都归类到 Electrical Engineering 中,也就是我们常说的EE。 …...

5.3 牛顿-科茨公式
学习目标: 理解微积分基础知识,例如导数和微分的概念。学习牛顿-科茨公式的推导过程。这个公式实际上是使用泰勒公式对被积函数进行展开,并使用微积分的基本原理进行简化得到的。学习如何使用牛顿-科茨公式进行数值积分。这通常涉及到将被积…...

全注解下的SpringIoc 续2-bean的生命周期
spring中bean的生命周期 上一个小节梳理了一下Spring Boot的依赖注入的基本知识,今天来梳理一下spring中bean的生命周期。 下面,让我们一起看看bean在IOC容器中是怎么被创建和销毁的。 bean的生命周期大致分为四个部分: #mermaid-svg-GFXNEU…...

【VQ-VAE代码实战】Neural Discrete Representation Learning
【VQ-VAE代码实战】Neural Discrete Representation Learning 0、前言1、简介2、Basic IdeaLoss3、代码Load DataVector Quantizer LayerEncoder & Decoder ArchitectureTrainPlot LossView ReconstructionsView EmbeddingReference0、前言 论文地址:基于神经网络的,离散…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
