信息的相关性和冗余度:信息在整个文明中的作用
文章目录
- I 古埃及的象形文字
- 1.1 罗塞塔石碑
- 1.2 古埃及文字音节和希腊字母的对应表
- 1.3 破解古埃及文字
I 古埃及的象形文字
1.1 罗塞塔石碑
这个石碑是在公元前196年埃及国王托勒密五世加冕一周年的诏书。
在此前大约一百年,埃及已经被来自希腊北方城邦的亚历山大大帝征服,被纳入了希腊文化圈。
亚历山大死后,他的部将托勒密自立为埃及法老,开始了埃及历史上的托勒密王朝,希腊文就成为了埃及的官方语言。
与此同时,埃及原有的文字也在使用,因此就出现了一碑三文的现象。
残缺的石碑,这上面刻有三种文字:
- 最上面是14行古埃及象形文
- 中间是32行埃及草书,是当时埃及平民使用的文字。
- 下面的54行则是古希腊文

1.2 古埃及文字音节和希腊字母的对应表
商博良一点点抽丝剥茧,逐渐破解了罗塞塔石碑上的内容,罗塞塔石碑便是开启以象形文字记载的古埃及文献秘密的金钥匙。

1.3 破解古埃及文字
靠信息冗余,可以恢复丢失掉的数据。从很多不同维度来描述一件事情,因此具有信息冗余,在丢失了一些维度的信息后,可以通过其它维度的信息补回来。
失传了的文字之所以能被破解,主要是因为相同的内容以不同的文字或者其他形式记录了很多遍。
相关文章:

信息的相关性和冗余度:信息在整个文明中的作用
文章目录 I 古埃及的象形文字1.1 罗塞塔石碑1.2 古埃及文字音节和希腊字母的对应表1.3 破解古埃及文字 I 古埃及的象形文字 1.1 罗塞塔石碑 这个石碑是在公元前196年埃及国王托勒密五世加冕一周年的诏书。 在此前大约一百年,埃及已经被来自希腊北方城邦的亚历山大…...
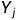
python数据结构与算法-动态规划(最长公共子序列)
一、最长公共子序列问题 1、问题概念 一个序列的子序列是在该序列中删去若干元素后得 到的序列。 例如:"ABCD”和“BDF”都是“ABCDEFG”的子序列。 最长公共子序列(LCS) 问题: 给定两个序列X和Y,求X和Y长度最大的公共子字列。 例:X"ABBCBDE”…...

Java版企业电子招投标系统源码 Spring Cloud+Spring Boot 电子招标采购系统功能清单
一、立项管理 1、招标立项申请 功能点:招标类项目立项申请入口,用户可以保存为草稿,提交。 2、非招标立项申请 功能点:非招标立项申请入口、用户可以保存为草稿、提交。 3、采购立项列表 功能点:对草稿进行编辑&#x…...
【c语言】函数的基本概念 | 函数堆栈调用原理
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
Vue.prototype 详解及使用
前言: 我们可能会在很多组件里用到数据/实用工具,但是不想污染全局作用域。这种情况下,可以通过在原型上定义它们使其在每个 Vue 的实例中可用。 1. 基本示例 在main.js中添加一个变量到 Vue.prototype Vue.prototype.$appName My App这…...

音视频八股文(3)--ffmpeg常见命令(2)
07-ffplay命令播放媒体 播放本地文件 播放本地 MP4 视频文件 test.mp4 的命令,从第 2 秒位置开始播放,播放时长为 10 秒,并且在窗口标题中显示 “test time”: ffplay -window_title "test time" -ss 2 -t 10 -autoe…...

使用bert4keras出现的问题(Process finished with exit code -1073741819 (0xC0000005))
1、环境 python 3.7.12 tensorflow 1.15 keras 2.3.1 bert4keras 0.9.7 protobuf 3.19.0 numpy 1.16.5 2、出现问题 numpy版本不兼容问题所以你就直接按照我的版本就可以了(numpy 1.16.5) Process finished with exit code -1073741819 (0xC0000005) …...
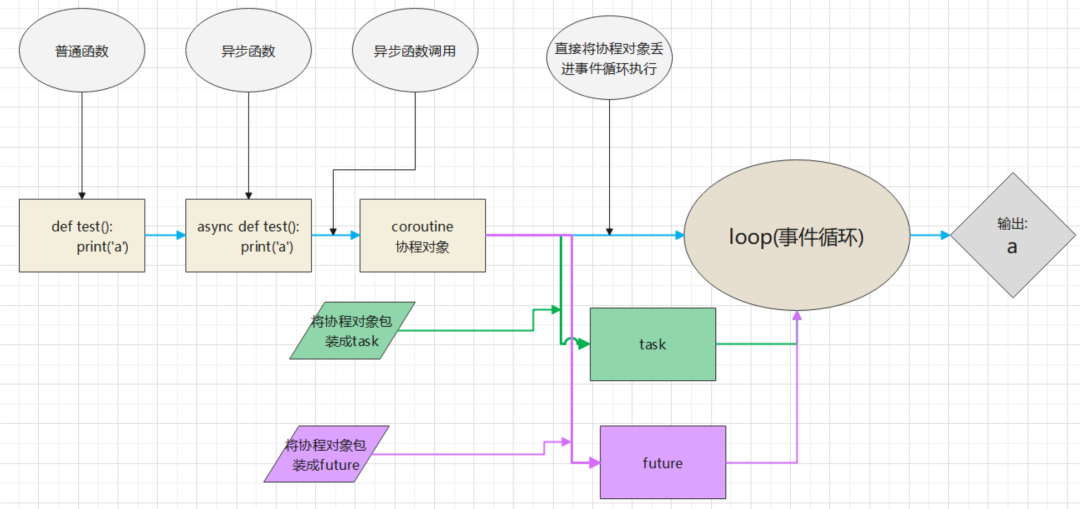
python协程实战
协程简介 协程(Coroutine)又称微线程、纤程,协程不是进程或线程,其执行过程类似于 Python 函数调用,Python 的 asyncio 模块实现的异步IO编程框架中,协程是对使用 async 关键字定义的异步函数的调用; 一个进程包含多个线程,类似…...
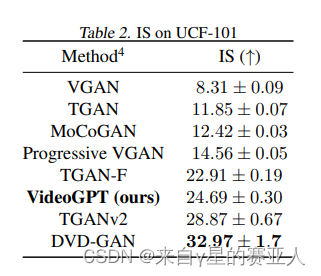
【论文笔记】VideoGPT: Video Generation using VQ-VAE and Transformers
论文标题:VideoGPT: Video Generation using VQ-VAE and Transformers 论文代码:https://wilson1yan. github.io/videogpt/index.html. 论文链接:https://arxiv.org/abs/2104.10157 发表时间: 2021年9月 Abstract 作者提出了…...
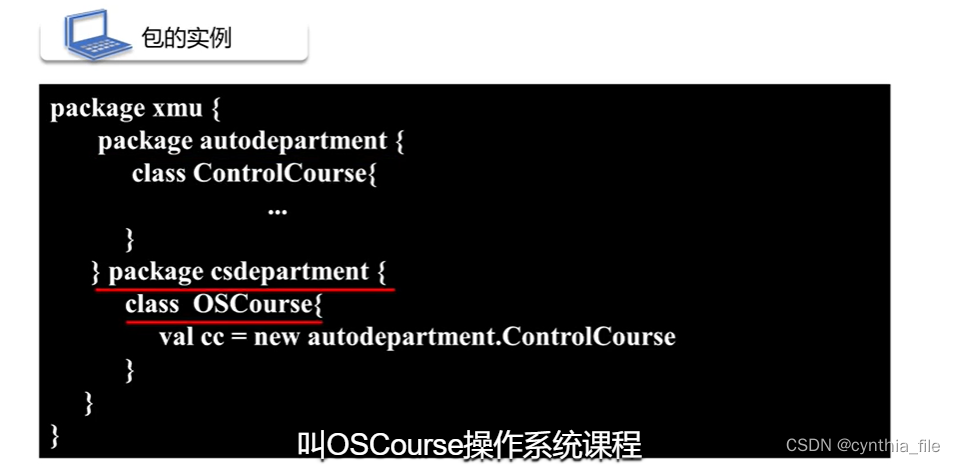
scala之基础面向对象
scala 既是面向对象 也是函数式编程 从Java 发展而来,依赖JVM环境 一、 scala 在linux中运行 scala 模式中直接编写运行 scala文件,load执行 scala编译程序 编译 运行 scala java 二、scala 数据类型 基础数据类型 val 不可变变量 函数式编程 …...

Qt5.12实战之多线程编程概念
1.为什么要使用多线程? a. 基于线程,同时处理多个任务,软件响应更灵敏 b.充分利用CPU的多核心功能增加应用运行效率 c.多线程在同一进程间使用共享通信更加高效 d.多个线程之间进行切换比多个进程之间进行切换,线程开销更少. 2.操作系统与进程关系 a. MS-DOS系统 属于单进程…...
格式化数据恢复怎么做?超实用的3种方法在这!
案例:格式化数据怎么恢复 【我的电脑前段时间中病毒了,无奈之下我只能将其格式化,但是很多重要的文件和图片之类的也一起被删除了,有什么方法可以恢复这些格式化的数据吗?非常着急!】 格式化数据恢复&…...

【Java|golang】1105. 填充书架---动态规划
给定一个数组 books ,其中 books[i] [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。 按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。 先选几本书放在书架上(它们的厚度之和小于等于书架的宽度 shelfWidt…...

linux基础命令
linux基础命令 一、linux命令 熟悉账务linux命令对运维的好处是巨大的,只有熟悉了命令咱们在运维的操作上才能如鱼得水。 系统信息 arch #显示机器的处理器架构(1) uname -m #显示机器的处理器架构(2) uname -r #显示正在使用的内核版本 dmidecode -q …...

【三十天精通Vue 3】 第十八天 Vue 3的国际化详解
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、Vue 3 国际化概述1.1 国际化的概念1.2 国际化的作用1.3 V…...

02 - 学会提问
学会提问 一、引言 1.1 GPT简介 GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的大型预训练语言模型。 凭借其强大的文本生成、理解和处理能力,GPT已在诸如自然语言处理、机器翻译、文本摘要等多个领域取得了显著的…...

Java经典的Main方法面试题
mian方法是做什么用的? main方法是Java程序的入口方法,JVM在运行的时候会首先查找main方法不用main方法如何运行一个类? 不行,没有main方法我们不能运行Java类 在Java7之前,你可以通过使用静态初始化运行Java类。但是&…...

世界大学电子电气工程TOP10,国内大学哪家强?
EE究竟是什么专业 ? 在中国,工程系中跟电相关的专业,一般都切分得非常细。有电子工程、电气工程、通信工程、信息工程、自动化、测控仪器等。但在国外,一般把这些领域都归类到 Electrical Engineering 中,也就是我们常说的EE。 …...

5.3 牛顿-科茨公式
学习目标: 理解微积分基础知识,例如导数和微分的概念。学习牛顿-科茨公式的推导过程。这个公式实际上是使用泰勒公式对被积函数进行展开,并使用微积分的基本原理进行简化得到的。学习如何使用牛顿-科茨公式进行数值积分。这通常涉及到将被积…...

全注解下的SpringIoc 续2-bean的生命周期
spring中bean的生命周期 上一个小节梳理了一下Spring Boot的依赖注入的基本知识,今天来梳理一下spring中bean的生命周期。 下面,让我们一起看看bean在IOC容器中是怎么被创建和销毁的。 bean的生命周期大致分为四个部分: #mermaid-svg-GFXNEU…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
