(1分钟速通面试) 矩阵分解相关内容
矩阵分解算法--总结
QR分解 LU分解
本篇博客总结一下QR分解和LU分解,这些都是矩阵加速的操作,在slam里面还算是比较常用的内容,这个地方在isam的部分出现过。(当然isam也是一个坑,想要出点创新成果的话 可能是不太现实的 短期来讲 哈哈哈)
假定我们能把矩阵A写成下列两个矩阵相乘的形式:A=LU,其中L为下三角矩阵,U为上三角矩阵。这样我们可以把线性方程组Ax= b写成Ax= (LU)x = L(Ux) = b。令Ux = y,则原线性方程组Ax = b可首先求解向量y 使Ly = b,然后求解 Ux = y,从而达到求解线性方程组Ax= b的目的。(非常熟悉的 数值分析课上学的LU分解的形式)

编辑
添加图片注释,不超过 140 字(可选)
LD(LT)的形式,就是把上面的LU分解中拆出来一个倍数矩阵,然后我觉得没啥必要。在这里也放上。
定理:若对称矩阵A的各阶顺序主子式不为零时,则A可以唯一分解为A= LDLT,这里。

编辑
添加图片注释,不超过 140 字(可选)
下面是cholesky分解 读作乔列斯基分解, 栓Q 这些英文名字要是不会读的话 你在讲相关内容的时候就会显得很尴尬 哈哈哈 笑死。
Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话,此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
对于上面这段定义,让我认知扩充了。上学期学的数值分析里面我知道是转置矩阵,但是没想到是共轭转置矩阵。也就是说一开始我是不知道他还有个共轭的关系在里面的。行了,现在知道了。可能上学期学的内容都是定义在实数域上面的,那么共轭的概念就逐渐被弱化了。现在记住了,原来是共轭转置矩阵。心里默念三遍 hhh
QR分解
矩阵的QR分解是指,可以将矩阵A分级成一个正交阵Q和一个上三角矩阵R的乘积。实际中,QR分解经常被用来解线性最小二乘问题。

编辑
添加图片注释,不超过 140 字(可选)
上面这个就是QR分解,感觉这些的话 会用就行,知道谁的速度快,然后什么情况下的矩阵适合什么样的方法即可。
SVD分解

编辑切换为居中
添加图片注释,不超过 140 字(可选)
说白了,这里的奇异值就是特征值的含义。那么这个矩阵的话,按照我本科的学习思路来说,就是由特征向量和特征值来共同组成的。就是那一套,莱姆大E - A的行列式,求特征值,特征向量,然后就写出来。现在的话,对特征值也是有一定的理解了。特征值可以反应数据的离散情况,也反映了数据的分布 同时可能也反映了数据的趋势。好了,这个特征值的话还是很有用的。在机器学习的一个面试题里面,特征值大的方向,数据会越离散,反之数据会越集中。当然我们研究的话,应该是研究离散的,因为这样好区分。前面这句话主要针对分类来说,因为你的数据离散了,可区分性好了以后,那么我们做分类的效果才显著,这样的研究才有意义。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
上面这幅图的话 主要说了广义逆矩阵的事情,为啥说是广义呢,因为平时我们定义的逆矩阵一定是一个方阵,这里不是方阵了,那么就称作是广义逆矩阵了。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
本科的时候我们叫他乔丹分解,哈哈哈 就是aj的那个乔丹。笑死。
这个没啥好说的,就是jardon块的构造,这个也是根据特征值的次数来进行构造的。可能再看一看就能想起来相关内容了,所以这里省略。(主要是slam里面好像并不提及这个东西,反正我是没见过 hhh)

编辑
添加图片注释,不超过 140 字(可选)
这里有一个比较。笑死,LU分解最快了。
那在这里对矩阵的分解进行一个总结。也就是说平时我们在解方程组的时候,如果求逆,会加大计算量。我们这时会选择矩阵分解的方法来进行求逆的代替。然后进而求得方程的解。笑死 我想起来上学期的考试,在线LU分解 在线cholesky分解,直接写结果,真的非常方便。如果按照它们的定义一步步地计算的话,我估计最起码20分钟 在不算错的情况下。行了 本篇就讲到这里,这个矩阵分解的内容,opencv也进行了相应地包装。在这里的话不必过多赘述了。栓Q,本篇到此结束。
相关文章:

(1分钟速通面试) 矩阵分解相关内容
矩阵分解算法--总结QR分解 LU分解本篇博客总结一下QR分解和LU分解,这些都是矩阵加速的操作,在slam里面还算是比较常用的内容,这个地方在isam的部分出现过。(当然isam也是一个坑,想要出点创新成果的话 可能是不太现实的 短期来讲 哈…...

this指向
(1)在全局环境中的this——window 无论是否在严格模式下,在全局执行环境中(在任何函数体外部)this 都指向全局对象。 "use strict"console.log(this); //windowconsole.log(thiswindow);//true (…...

安卓小游戏:小板弹球
安卓小游戏:小板弹球 前言 这个是通过自定义View实现小游戏的第三篇,是小时候玩的那种五块钱的游戏机上的,和俄罗斯方块很像,小时候觉得很有意思,就模仿了一下。 需求 这里的逻辑就是板能把球弹起来,球…...
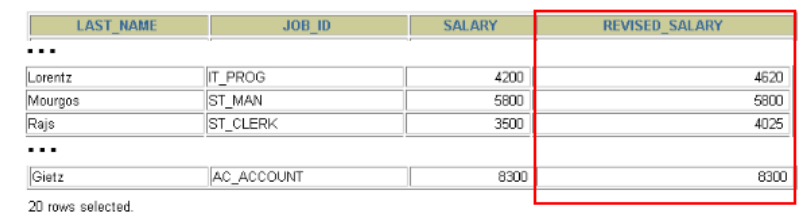
7、单行函数
文章目录1 函数的理解1.1 什么是函数1.2 不同DBMS函数的差异1.3 MySQL的内置函数及分类2 数值函数2.1 基本函数2.2 角度与弧度互换函数2.3 三角函数2.4 指数与对数2.5 进制间的转换3 字符串函数4 日期和时间函数4.1 获取日期、时间4.2 日期与时间戳的转换4.3 获取月份、星期、星…...
)
华为机试题:HJ56 完全数计算(python)
文章目录博主精品专栏导航知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方法2、print() :打印输出。3、整型int() :将指定进制…...

opencv——傅里叶变换、低通与高通滤波及直方图等操作
1、傅里叶变换a、傅里叶变换原理时域分析:以时间为参照进行分析。频域分析:相当于上帝视角一样,看事物层次更高,时域的运动在频域来看就是静止的。eg:投球——时域分析:第1分钟投了3分,第2分钟投…...
【NGINX入门指北】 进阶篇
nginx 进阶篇 文章目录nginx 进阶篇一、Nginx Proxy 服务器1、代理原理2、proxy代理3、proxy缓存一、Nginx Proxy 服务器 1、代理原理 正向代理 内网客户机通过代理访问互联网,通常要设置代理服务器地址和端口。 反向代理 外网用户通过代理访问内网服务器&…...

Python中关于@修饰符、yeild关键词、next()函数的基本功能简述
关于修饰符:其实就是将修饰符下面的函数当成参数传给它上面的函数。 def a(x):print(a)adef b():print(b) 其效果等价为: def a(x):print(a)def b():print(b)a(b())有个记忆诀窍,的下面哪个函数最近,谁就是儿子,谁就…...

结合Coverity扫描Spring Boot项目进行Path Manipulation漏洞修复
本篇介绍使用Coverity 扫描基于Spring Boot 项目中的Path Manipulation 漏洞, 进而解决风险,并且可以通过扫描。 什么样的代码会被扫描有路径操纵风险? 在Spring Boot 项目中, 实验了如下的场景: 1. Control 中 file path 作为参数传递的会被扫描,单纯服务方法不会 场…...

【FFMPEG源码分析】从ffplay源码摸清ffmpeg框架(一)
ffplay入口 ffmpeg\fftools\ffplay.c int main(int argc, char **argv) {/*******************start 动态库加载/网络初始化等**************/int flags;VideoState *is;init_dynload();av_log_set_flags(AV_LOG_SKIP_REPEATED);parse_loglevel(argc, argv, options);/* regis…...

C++蓝桥杯 基础练习,高精度加法,输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。
C蓝桥杯 基础练习,高精度加法 问题描述 输入两个整数a和b,输出这两个整数的和。a和b都不超过100位。 算法描述 由于a和b都比较大,所以不能直接使用语言中的标准数据类型来存储。对于这种问题,一般使用数组来处理。 定义一…...
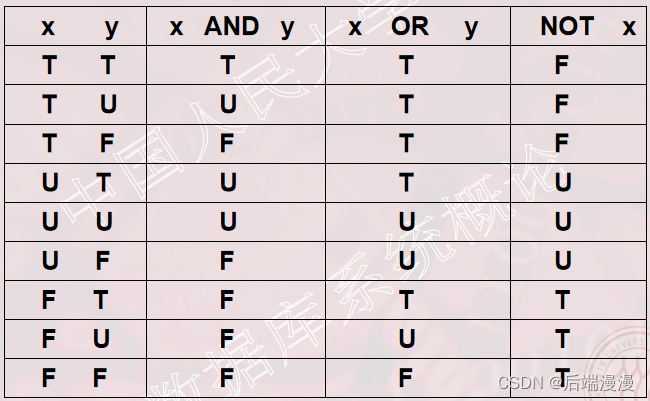
MySQL面试题:SQL语句的基本语法
MySQL目录一、数据库入门1. 数据管理技术的三个阶段2. 关系型数据库与非关系型数据库3. 四大非关系型数据库a. 基于列的数据库(column-oriented)b. 键值对存储(Key-Value Stores)c. 文档存储(Document Storesÿ…...
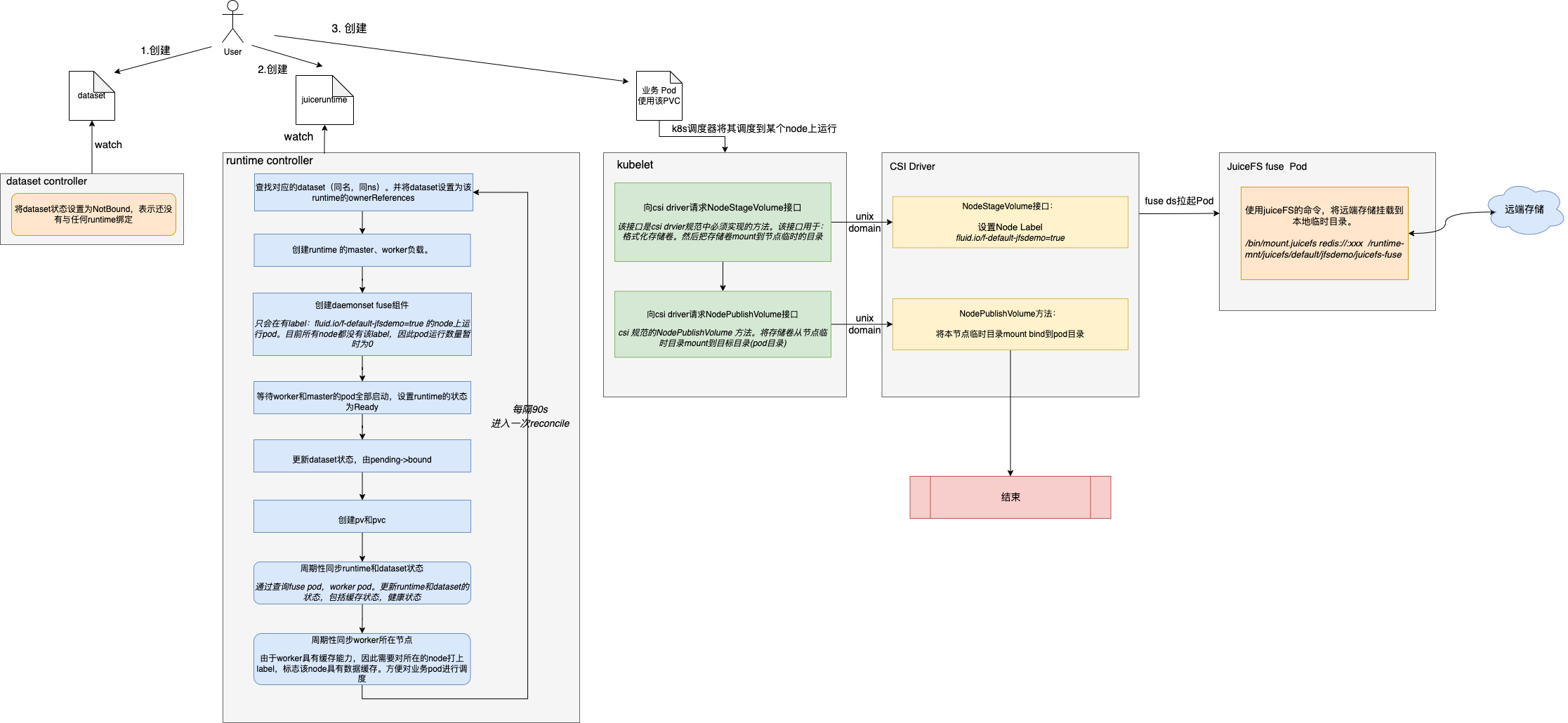
Fluid-数据编排能力原理解析
前言本文对Fluid基础功能-数据编排能力进行原理解析。其中涉及到Fluid架构和k8s csi driver相关知识。建议先了解相关概念,为了便于理解,本文使用JuiceFS作为后端runtime引擎。原理概述Fuild数据编排能力,主要是在云原生环境中,能…...
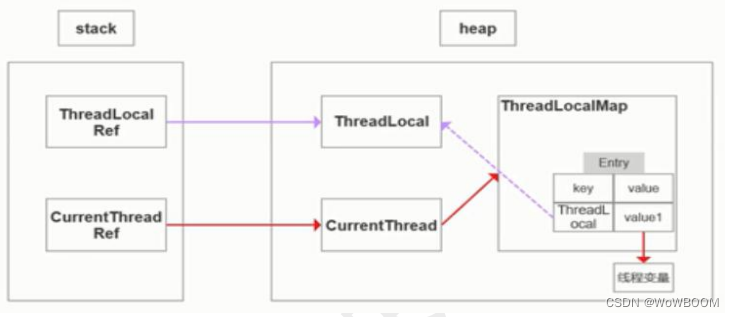
并发线程、锁、ThreadLocal
并发编程并发编程Java内存模型(JMM)并发编程核心问题—可见性、原子性、有序性volatile关键字原子性原子类CAS(Compare-And-Swap 比较并交换)ABA问题Java中的锁乐观锁和悲观锁可重入锁读写锁分段锁自旋锁共享锁/独占锁公平锁/非公平锁偏向锁/轻量级锁/重…...

CMMI-结项管理
结项管理(ProjectClosing Management, PCM)是指在项目开发工作结束后,对项目的有形资产和无形资产进行清算;对项目进行综合评估;总结经验教训等。结项管理过程域是SPP模型的重要组成部分。本规范阐述了结项管理的规程&…...
网络通信协议是什么?
网络通信基本模式 常见的通信模式有如下2种形式:Client-Server(CS) 、 Browser/Server(BS) 实现网络编程关键的三要素 IP地址:设备在网络中的地址,是唯一的标识。 端口:应用程序在设备中唯一的标识。 协议: 数据在网络中传输的…...

阶段5:Java分布式与微服务实战
目录 第33-34周 Spring Cloud电商实战 一、Eureka-server模块开发 1、引入依赖 2、配置文件 3、启动注解 一、Eureka-server模块开发 第33-34周 Spring Cloud电商实战 一、Eureka-server模块开发 1、引入依赖 父项目依赖:cloud-mall-practice springboot的…...

我的创作纪念日
目录 机缘 收获 日常 憧憬 机缘 其实本来从大一上学期后半段(2017)就开始谢谢零星的博客,只不过当时是自己用hexo搭建了一个小网站,还整了个域名:jiayoudangdang.top,虽然这个早就过期; 后来发现了CSDNÿ…...
Qml学习——动态加载控件
最近在学习Qml,但对Qml的各种用法都不太熟悉,总是会搞忘,所以写几篇文章对学习过程中的遇到的东西做一个记录。 学习参考视频:https://www.bilibili.com/video/BV1Ay4y1W7xd?p1&vd_source0b527ff208c63f0b1150450fd7023fd8 目…...

设计模式之职责链模式
什么是职责链模式 职责链模式是避免请求发送者与接受者耦合在一起,让多个对象都可以接受到请求,从而将这些对象连接成一条链,并且沿着这条链传递请求,直到有对象处理为止。 职责链模式包含以下几个角色: …...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...
