数学建模第七天:数学建模算法篇之插值及MATLAB实现
目录
一、前言
1、引例
2、拟合定义
3、拟合与插值的关系
二、拟合
1、线性最小二乘法求解
①思路
②解法
2、MATLAB对线性最小二乘拟合的实现
①函数说明
②求解例题
3、MATLAB实现非线性曲线拟合
①lsqcurvefit函数
②代码求解
4、MATLAB实现非线性最小二乘拟合
①lsqnonlin函数
②代码求解
一、前言
1、引例
话不多说,我们还是老规矩,上例题!
伍老师当了这么多篇文章的主角,今天的主角终于成为了伍老师的闺蜜汪老师。汪老师的零花钱一般在月初发,但是,汪老师一不小心多网购了一点,四月的最后一周只剩下了300块钱。已知这一周的前四天开销如下:
4月24号:踌躇满志的想要去省钱,当天花销共计35块
4月25号:感觉最后一周的第一天太克制自己了,多花一点,当天花销共计45块
4月26号:陪男朋友出去玩,多点了一杯奶茶,当天花销共计48块、
4月27号:突然发现前两天花的钱有点多了,克制一下,当天花销共计38块
那么,请你预测一下汪老师的花销函数,并且估计,300块汪老师能否撑过这一周?
2、拟合定义
曲线拟合问题是指:已知平面上n个点,i=1,2,3……n,
互不相同。寻求函数f(x),使f(x)在某种准则下与所有数据点最为接近,即曲线拟合得很好。比如说我们高中学习过电阻与温度相关,我们测量某几个温度下的电阻,做出一条线,这就是我们拟合出来的函数图像:

曲线拟合一般需要解决如下两个问题:
①线型的选择;
②线型中参数的计算
其中,问题①是拟合问题的关键与难点,线性拟合中参数的计算可以使用最小二乘法,二非线性拟合参数的计算则要应用GN迭代法。
3、拟合与插值的关系
相同点:给定一批数据点,需确定满足特定要求的曲线或曲面
不同点:若要求所求曲线(面)通过所给所有数据点,就是插值问题;不要求曲线(面)通过所有数据点,而是要求它反映对象整体的变化趋势,这就是数据拟合,又称曲线拟合或曲面拟合。像上篇文章中出现过Runge现象,当不小于7次时,波动十分显著,所以我们需要用拟合的方法去构建相关的函数。小编借用龙门飞甲里的几句台词,来说明拟合的作用:
“拟合算什么东西?”
“你问我拟合算什么东西,现在我就来告诉你。插值算不了的值由我拟合来做,插值画不了的图我画,插值写不了的代码我写。一句话,拟合建不了的模我要建。拟合建不了的模我更要建!这就是西厂!”
函数插值与曲线拟合都是要根据一组数据构造一个函数作为近似,由于近似的要求不同,二者在数学方法上是完全不同的。
二、拟合
1、线性最小二乘法求解
①思路
第一步:先选定一组函数 ,
,……,
, m<n, 令
( 1 )
其中,
, …,
为待定系数。
第二步: 确定,
, …,
的准则(最小二乘准则): 使n个点
与曲线 y=f(x) 的距离
的平方和最小

问题归结为,求 ,
,……,
,使
最小
②解法
我们把方程个数大于未知量个数的方程组称为超定方程组:

我们可以把上述超定方程组简写为矩阵乘法形式:

超定方程组一般是不存在解的矛盾方程组,所以我们定义如果有向量a使得式子(4)达到最小, 则称a为上述超定方程组的最小二乘解。
这里补充一个定理:当可逆时,超定方程组(3)存在最小二乘解,且即为方程组
2、MATLAB对线性最小二乘拟合的实现
①函数说明
调用函数:
a=polyfit(x,y,m)参数说明:
a:输出拟合多项式系数 a=[a1, …,am , am+1] (数组))
x、y:输入同长度的数组x,y,为已知的点坐标
m:拟合多项式次数
作用:对多项式拟合
额外说明:
对超定方程组,可以用a=R\y得到最小二乘意义下的解。
多项式在x处的值y可用y=polyval(a,x)命令计算。
②求解例题
如果使用一次函数拟合,则代码为:
x=[1,2,3,4];
y=[35,45,48,38];
A=polyfit(x,y,1)
x1=1:1:7
z=polyval(A,x1)
plot(x,y,'o',x1,z,'r')
求出的结果为:


所以预计最后三天汪老师会花费44.5+45.7+46.9=137.1元,算上前面四天的消费,一共303.1元,故汪老师三百块撑不过这一周,需要找伍老师接三块一毛钱。
3、MATLAB实现非线性曲线拟合
①lsqcurvefit函数
已知输入数据点和输出数据点,即x=(xdata1,xdata2,……,xdatan),y=(ydata1,ydata2,……ydatan),并且还知道输入数据点与输出数据点的关系为ydata=F(x,xdata),MATLAB里有lsqcurvefit函数能够对曲线进行拟合,求得x使得下式成立:

函数输出格式:
x = lsqcurvefit (‘fun’,x0,xdata,ydata);
x =lsqcurvefit(‘fun’,x0,xdata,ydata,options);
x=lsqcurvefit(‘fun’,x0,xdata,ydata,options,’grad’);
参数说明:
其中x0代表初始解向量,option代表优化方式,xdata与ydata满足ydata=F(x,xdata),fun代表一个事先建立的定义函数F(x,xdata) 的m文件, 自变量为x和xdata。
②代码求解
加入我们知道汪老师最后一周的花销函数为,请用lsqcurvefit函数拟合,并且求出参数a、w、k、b。
我们先定义一个花销函数expense.m,内容如下:
function F=expense(x,xdata);F=-x(1)*cos(x(2)*xdata)+x(3)*xdata+x(4)% x(1)=a; x(2)=w,x(3)=k,x(4)=b;再输入相关命令:
xdata=[1,2,3,4];
ydata=[35,45,48,38];
x0=[0.1,0.1,0.1,0.1];x=lsqcurvefit('expense',x0,xdata,ydata)xnew=1:1:7;F=expense(x,xnew)我们就能算出,a、w、k、b四个参数的值以及汪老师这一周每天的花费,如下:

再计算一下这一周的后三天汪老师会花费48.07+48.43+46.6=143.1,而按照这个模型这一周共计花费309.1元,看来300是不够的,还需要多找伍老师借9.1块钱。
4、MATLAB实现非线性最小二乘拟合
①lsqnonlin函数
已知输入数据点和输出数据点,即x=(xdata1,xdata2,……,xdatan),y=(ydata1,ydata2,……ydatan),用以求含参量x的向量值函数f(x),使得下式的值最小:

其中fi(x)=f(x,xdatai,ydatai)=F(x,xdatai)-ydatai。
函数格式:
x=lsqnonlin(‘fun’,x0)
x=lsqnonlin(‘fun’,x0,options)
x= lsqnonlin('fun’,x0,options‘grad’)
参数说明:
其中x0代表初始解向量,option代表优化方式,fun代表一个事先建立的定义函数F(x) 的m文件, 自变量为x。
②代码求解
仍然以刚刚那道题为例,我们先定义一个花销函数expense.m,内容如下:
function F=expense(x);
xdata=[1,2,3,4];
ydata=[35,45,48,38];F=-x(1)*cos(x(2)*xdata)+x(3)*xdata+x(4)% x(1)=a; x(2)=w,x(3)=k,x(4)=b;再输入代码:
x0=[0.1,0.1,0.1,0.1];x=lsqnonlin('expense',x0)xnew=1:1:7;F=expense(x)就能算出各个参数的值!结果与非线性曲线拟合的结果一致,这里就不放相应的结果啦!
好的,本期的数学建模的课程就到这里啦,不知道小编的文章对各位观众老爷们有没有帮助呢?麻烦大家给小编点一个免费的小心心好吗?
相关文章:

数学建模第七天:数学建模算法篇之插值及MATLAB实现
目录 一、前言 1、引例 2、拟合定义 3、拟合与插值的关系 二、拟合 1、线性最小二乘法求解 ①思路 ②解法 2、MATLAB对线性最小二乘拟合的实现 ①函数说明 ②求解例题 3、MATLAB实现非线性曲线拟合 ①lsqcurvefit函数 ②代码求解 4、MATLAB实现非线性最小二乘拟…...

RUST 每日一省:生命周期作用域
生命周期 一个变量的生命周期就是它从创建到销毁的整个过程。 作用域 我们声明的每个变量都有作用域。作用域其实是变量和值存在的环境。作用域是由一对花括号表示的。例如,使用块表达式会创建一个作用域,即任何以花括号开头和结尾的表达式。此…...

【过程8】——能量守恒视角总结感受
一、背景 另一个角度的看到,观望着过程中自己曾经类似的经历(小舅子的工作)。 时间久了,经历多了,感悟会更加的充实;最近自己对于人在维持能量的过程中也有很多的感悟,一并做一下总结 二、过程 1.人为什么天性不愿意…...
kong(4):限流配置
Kong 提供了 Rate Limiting 插件,实现对请求的限流功能,避免过大的请求量过大,将后端服务打挂。 Rate Limiting 支持秒/分/小时/日/月/年多种时间维度的限流,并且可以组合使用。例如说:限制每秒最 多 100 次请求&…...
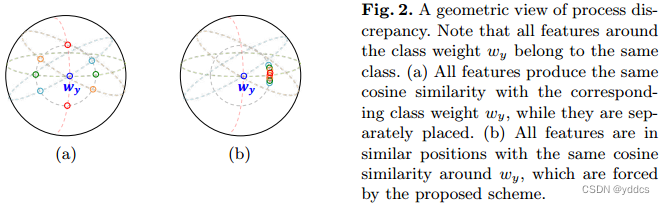
人脸识别 Face Recognition 入门
人脸识别 Face Recognition 入门概述 总述传统特征方法深度学习方法损失函数改进基于欧几里德和距离的损失基于角度/余弦边距的损失SoftMax 损失及其变体 一级标题二级标题二级标题二级标题 找论文搭配 Sci-Hub 食用更佳 💪 Sci-Hub 实时更新 : https://tool.yovisu…...

【AI绘画】Midjourney的使用及程序示例
Midjourney 1.背景2.Midjourney的原理3.Midjourney的使用方法4.Midjourney的示例代码 1.背景 Midjourney 是一款基于深度学习的图像转换工具,其可以将一张图像转换成具有不同风格的图像,例如将一张照片转换成卡通风格的图像。Midjourney 基于 TensorFlow…...
无公网IP?教你在外远程访问本地wamp服务器「内网穿透」
目录 前言 1.Wamp服务器搭建 1.1 Wamp下载和安装 1.2 Wamp网页测试 2. Cpolar内网穿透的安装和注册 2.1 本地网页发布 2.2 Cpolar云端设置 2.3 Cpolar本地设置 3. 公网访问测试 4. 结语 前言 软件技术的发展日新月异,各种能方便我们生活、工作和娱乐的新…...

leetcode 628. 三个数的最大乘积
题目描述解题思路执行结果 leetcode 628. 三个数的最大乘积 题目描述 三个数的最大乘积 给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。 示例 1: 输入:nums [1,2,3] 输出:6 示例 2&…...

fork函数如何创建进程,exit/_exit函数如何使进程终止的详细分析与代码实现
🎊【进程通信与并发】专题正在持续更新中,进程,线程,IPC,线程池等的创建原理与运用✨,欢迎大家前往订阅本专题,获取更多详细信息哦🎏🎏🎏 🪔本系列…...

重置电脑时提示“缺少所需的驱动器分区”怎么办?
当您启动Windows 10电脑并收到“您的电脑/设备需修复”这个消息提示时,您会马上尝试修复电脑,如果您这样做了,您可能会收到一个“安装Windows的驱动器已被锁定”的信息。如果您尝试重置您的电脑,您可能会收到一条提示,…...
在KylinV10安装Dm8
前言 因为近期,业外和几个朋友想搞点有趣的项目玩玩,既然不以盈利为主,就> 主推国产化,所以这篇记录一下,我在KylinV10安装dm8.最近真的很忙,要负责专研一下国产化工具开发的事,还要负责tb级…...

「SQL面试题库」 No_46 交换工资
🍅 1、专栏介绍 「SQL面试题库」是由 不是西红柿 发起,全员免费参与的SQL学习活动。我每天发布1道SQL面试真题,从简单到困难,涵盖所有SQL知识点,我敢保证只要做完这100道题,不仅能轻松搞定面试࿰…...
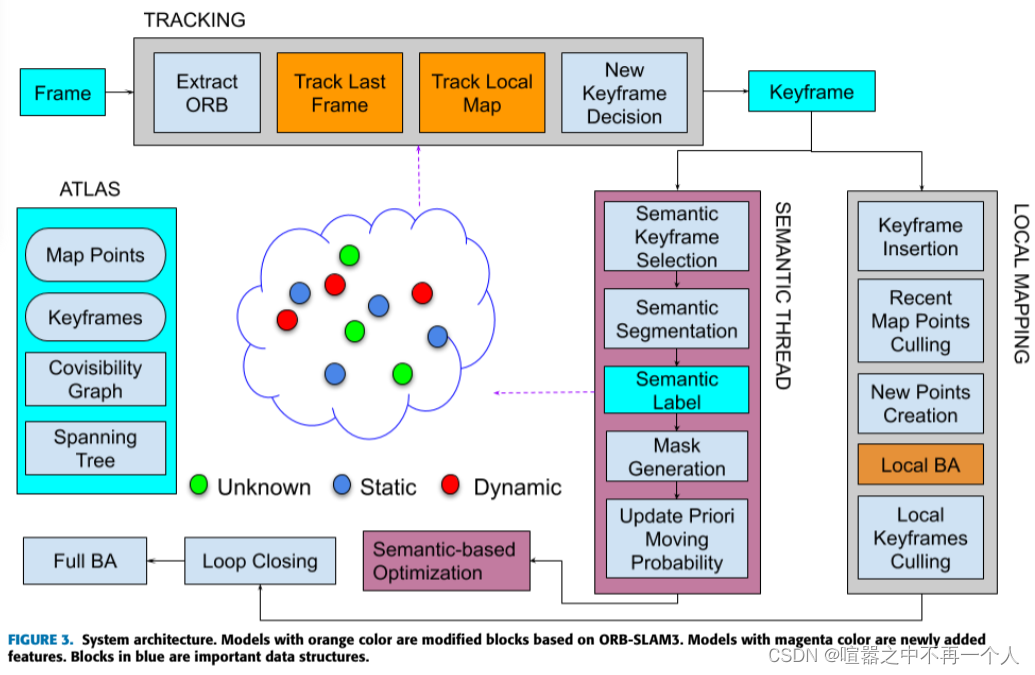
SLAM论文速递【SLAM—— RDS-SLAM:基于语义分割方法的实时动态SLAM—4.24(1)
论文信息 题目: RDS-SLAM:Real-Time Dynamic SLAM Using Semantic Segmentation Methods RDS-SLAM:基于语义分割方法的实时动态SLAM论文地址: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber9318990发表期刊: IEEE Access ( Volum…...
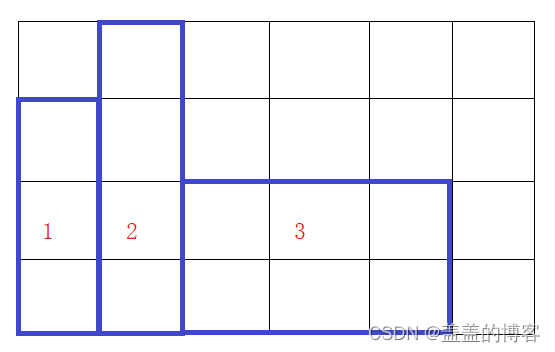
OJ练习第82题——填充书架
填充书架 力扣链接:1105. 填充书架 题目描述 给定一个数组 books ,其中 books[i] [thicknessi, heighti] 表示第 i 本书的厚度和高度。你也会得到一个整数 shelfWidth 。 按顺序 将这些书摆放到总宽度为 shelfWidth 的书架上。 先选几本书放在书架…...

OHOS IDE和SDK的安装方法
参照OpenHarmony应用开发环境安装流程,下载安装OHOS的IDE,过程中需要全程联网。 IDE,安装至D:\Tools\Huawei\DevEcoStudio。 IDE安装成功之后,按照提示下载安装HOS和OHOS的SDK。 nodejs,安装至D:\Tools\Huawei\nodejs…...
)
New Year Garland(计数类DP)
New Year Garland 题意 用m种颜色的球装饰n层的圣诞树,圣诞树的第i层由 l i l_{i} li个彩球串成,且同一层相邻的球颜色不同,相邻的层之间彩球颜色的集合不同,问有多少种方案,对p取模。 分析 首先先计算每一…...

32岁阿里P7,把简历改成不知名小公司,学历改成普通本科,工作内容不变,投简历全挂!...
hr靠什么来招人? 一位猎头讲述了自己和朋友打赌的故事: 朋友在阿里云,32岁,P7,他把简历上的公司改成不知名,学历改成普通本科,工作内容不变,结果投其他公司(比如京东&…...
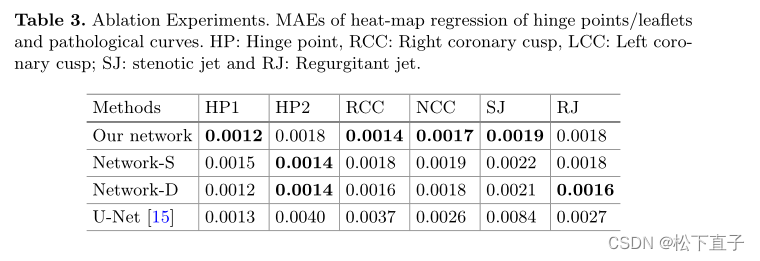
从三室心脏MRI影像检测主动脉瓣病变
Detecting Aortic Valve Pathology from the 3-Chamber Cine Cardiac MRI View 摘要 背景 心脏磁共振(CMR)是量化心脏容量、功能和血流量的金标准。定制的MR脉冲序列定义了对比机制,采集几何形状和定时,可以在CMR期间应用,以实现独特的组织…...
【JavaWeb】JavaScript
1、JavaScript 介绍 Javascript 语言诞生主要是完成页面的数据验证。因此它运行在客户端,需要运行浏览器来解析执行 JavaScript 代码。 JS 是 Netscape 网景公司的产品,最早取名为 LiveScript;为了吸引更多 java 程序员。更名为 JavaScript。 JS 是弱…...

Apache Doris 1.2.4 Release 版本正式发布|版本通告
亲爱的社区小伙伴们,我们很高兴地宣布,Apache Doris 于 2023 年 4 月 27 日迎来 1.2.4 Release 版本的正式发布!在 1.2.4 版本中,Doris 团队已经修复了自 1.2.3 版本发布以来近 150 个问题或性能改进项。同时,1.2.4 版…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
