【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】

| 🚀 算法题 🚀 |
🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨
🌲 作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步?🎯🎯
| 🚀 算法题 🚀 |

🍔 目录
- 🚗 知识回顾
- 🚩 题目链接
- ⛲ 题目描述
- 🌟 求解思路&实现代码&运行结果
- ⚡ 暴力递归
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 记忆化搜索
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- ⚡ 动态规划
- 🥦 求解思路
- 🥦 实现代码
- 🥦 运行结果
- 💬 共勉
🚗 知识回顾
该题和我们之前的题目在求解的思路上相似之处,感兴趣的同学可以学习一下相关的内容。
- 【LeetCode: 1043. 分隔数组以得到最大和 | 暴力递归=>记忆化搜索=>动态规划 | 线性dp & 区间dp】
- 【LeetCode: 2369. 检查数组是否存在有效划分 | 暴力递归=>记忆化搜索=>动态规划 | 线性dp】
- 【LeetCode: 1105. 填充书架 | 暴力递归=>记忆化搜索=>动态规划 | 线性dp & 业务限制】
🚩 题目链接
- 1416. 恢复数组
⛲ 题目描述
某个程序本来应该输出一个整数数组。但是这个程序忘记输出空格了以致输出了一个数字字符串,我们所知道的信息只有:数组中所有整数都在 [1, k] 之间,且数组中的数字都没有前导 0 。
给你字符串 s 和整数 k 。可能会有多种不同的数组恢复结果。
按照上述程序,请你返回所有可能输出字符串 s 的数组方案数。
由于数组方案数可能会很大,请你返回它对 10^9 + 7 取余 后的结果。
示例 1:
输入:s = “1000”, k = 10000
输出:1
解释:唯一一种可能的数组方案是 [1000]
示例 2:
输入:s = “1000”, k = 10
输出:0
解释:不存在任何数组方案满足所有整数都 >= 1 且 <= 10 同时输出结果为 s 。
示例 3:
输入:s = “1317”, k = 2000
输出:8
解释:可行的数组方案为 [1317],[131,7],[13,17],[1,317],[13,1,7],[1,31,7],[1,3,17],[1,3,1,7]
示例 4:
输入:s = “2020”, k = 30
输出:1
解释:唯一可能的数组方案是 [20,20] 。 [2020] 不是可行的数组方案,原因是 2020 > 30 。 [2,020] 也不是可行的数组方案,因为 020 含有前导 0 。
示例 5:
输入:s = “1234567890”, k = 90
输出:34
提示:
1 <= s.length <= 10^5.
s 只包含数字且不包含前导 0 。
1 <= k <= 10^9.
🌟 求解思路&实现代码&运行结果
⚡ 暴力递归
🥦 求解思路
- 该题目让我们求解的是将s进行一个划分,每一个划分的部分都小于等于k的总体方案数。
- 总体求解思路还是动态规划,为什么呢?因为我们想要求解的是从0位置开始,到s的最后一个位置结束,满足每个部分小于等于k的总体方案数目。如果说我们此时划分了0-cur位置,那么从cur-最后一个结束位置还需要重复这个过程,所以说,该过程是存在重复子问题的,我们可以通过动态规划来进行一个求解。
- 首先,我们还是设计一个递归函数,递归函数的含义是从index位置开始进行划分,找到所有满足的方案数。
🥦 实现代码
class Solution {private int mod=(int) 1e9 + 7;public int numberOfArrays(String s, int k) {return (int)(process(0,s,k)%mod);}public long process(int index,String s,int k){if(index>=s.length()){return 1;}long res=0;for(int i=index;i<s.length();i++){long sum=0;for(int j=index;j<i+1;j++){sum=sum*10+s.charAt(j)-'0';}if(s.substring(index,i+1).charAt(0)!='0'&&sum<=k&&sum>=1){res+=process(i+1,s,k)%mod;}}return res%mod;}
}
🥦 运行结果
时间超限了,不要紧哦,我还有锦囊妙计!
⚡ 记忆化搜索
🥦 求解思路
- 根据我们递归的分析,在递归的过程中会产生重复的子过程,所以我们想到了加一个缓存表,也就是我们的记忆化搜索。
- 因为题目给定我们的k的限制条件是k≤10^9 ,所以我们最多只要枚举 10个数字就行了,这个也是我们优化的一个点,否则时间还是会超限的。
🥦 实现代码
class Solution {private int mod=(int) 1e9 + 7;private long[] dp;public int numberOfArrays(String s, int k) {dp=new long[s.length()];Arrays.fill(dp,-1);return process(0,s,k)%mod;}public int process(int index,String s,int k){if(index>=s.length()){return 1;}if(dp[index]!=-1) return (int)(dp[index]);long res=0;long sum=0,base=10;for(int i=index;i<s.length()&&i-index<=10;i++){if(s.substring(index,i+1).charAt(0)=='0') continue;sum=sum*base+s.charAt(i)-'0';if(sum<=k&&sum>=1){res+=process(i+1,s,k)%mod;}}return (int)(dp[index]=res%mod);}
}
🥦 运行结果
⚡ 动态规划
🥦 求解思路
- 按照我们之前递归和记忆化搜索的思路,通过动态规划实现出来。
🥦 实现代码
class Solution {private int mod=(int) 1e9 + 7;private long[] dp;public int numberOfArrays(String s, int k) {int n=s.length();dp=new long[n+1];dp[n]=1;for(int index=n-1;index>=0;index--){long res=0;long sum=0,base=10;for(int i=index;i<s.length()&&i-index<=10;i++){if(s.substring(index,i+1).charAt(0)=='0') continue;sum=sum*base+s.charAt(i)-'0';if(sum<=k&&sum>=1){res+=dp[i+1]%mod;}}dp[index]=res%mod;}return (int)(dp[0]%mod);}
}
🥦 运行结果
💬 共勉
| 最后,我想和大家分享一句一直激励我的座右铭,希望可以与大家共勉! |


相关文章:

【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
centos7查看磁盘io
1.查看所使用到的命令为iostat,centos7没有自带iostat,需要安装一下 2.安装iostat命令 yum -y install sysstat 3.使用iostat命令 iostat %user:表示用户空间进程使用 CPU 时间的百分比 %nice:表示用户空间进程以降低优先级的…...
浅析低代码开发的典型应用构建场景v
在数字经济蓬勃发展的大势之下,企业软件开发人员供给不足、开发速度慢、开发成本高、数字化和智能化成效不明显等问题日益凸出,阻碍了企业的数字化转型。 而近年来,低代码的出现推动了经济社会的全面提效,也成为人才供求矛盾的润…...
3 连续模块(二)
3.5 零极点增益模块 在控制系统设计和分析中,常用的函数包括 传递函数(tf)、零极点(zpk)和状态空间(ss)函数 传递函数(tf):用于表示线性时不变系统的输入输出…...
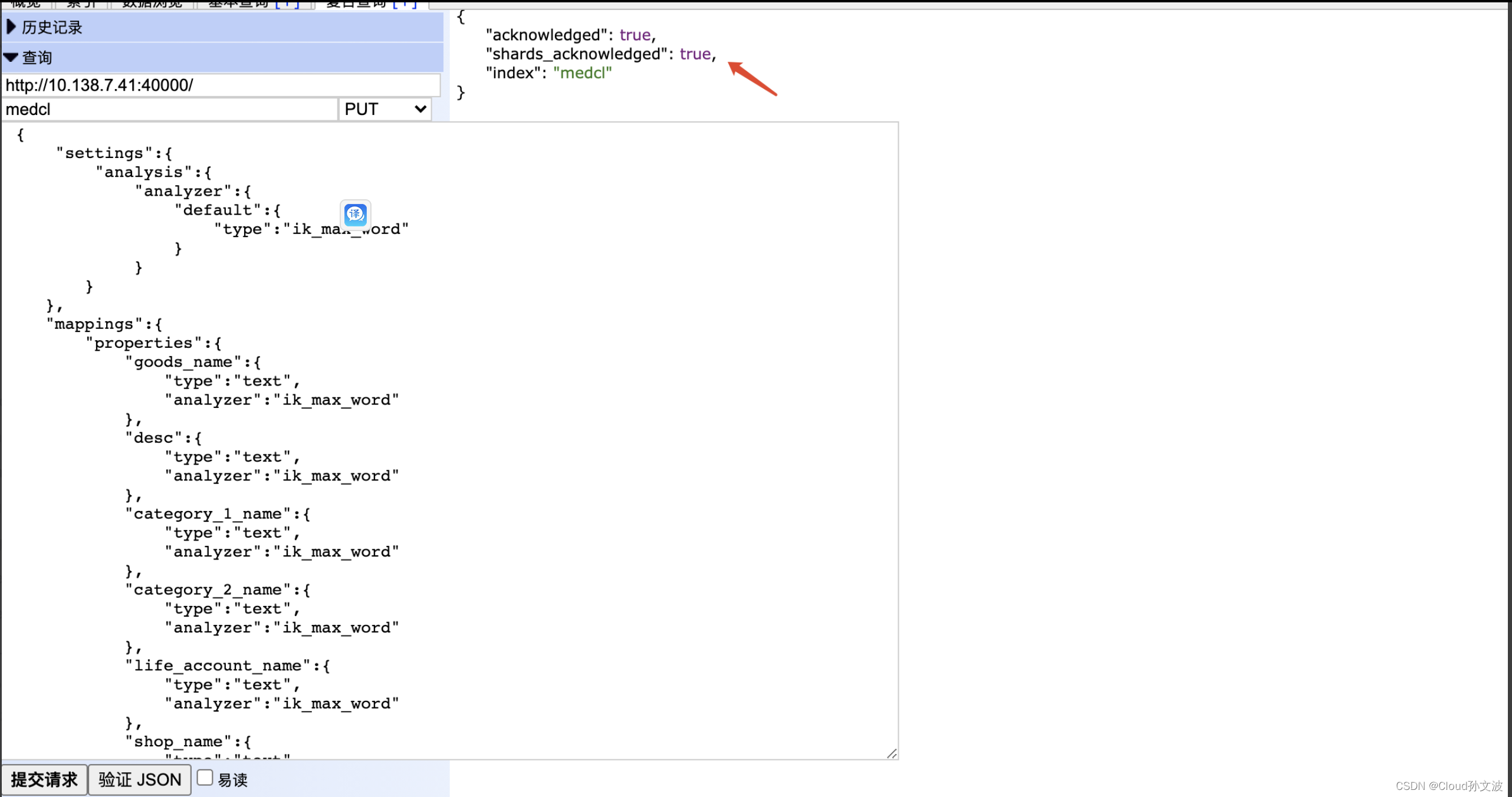
ElasticSearch 部署及安装ik分词器
ansiable playbook链接: https://download.csdn.net/download/weixin_43798031/87719490 需要注意的点:公司es集群现以三个角色部署分别为 Gateway、Master、Data 简单的理解可以理解为在每台机器上部署了三个es,以端口和配置文件来区分这三…...
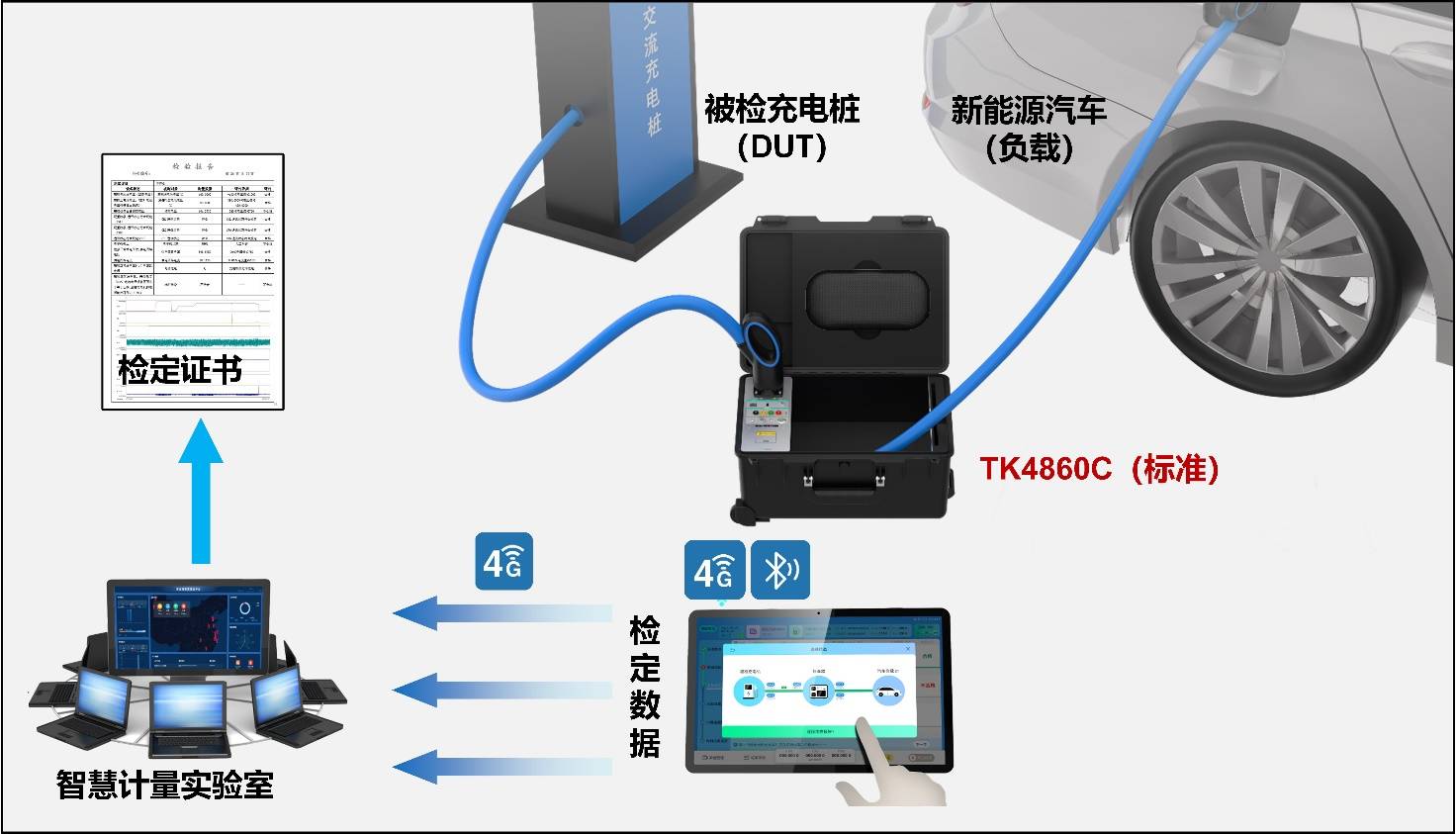
汽车充电桩检测设备TK4860C交流充电桩检定装置
TK4860C是一款在交流充电桩充电过程中实时检测充电电量的标准仪器,仪器以新能源车为负载,结合宽动态范围测量技术、电能ms级高速刷新等技术,TK4860C实现充电全过程的累积电能精准计量,相比于传统的预设检定点的稳态计量࿰…...

备份和恢复:确保数据安全
备份和恢复:确保数据安全 在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。 备份策略概述 在制定备份策略时&…...
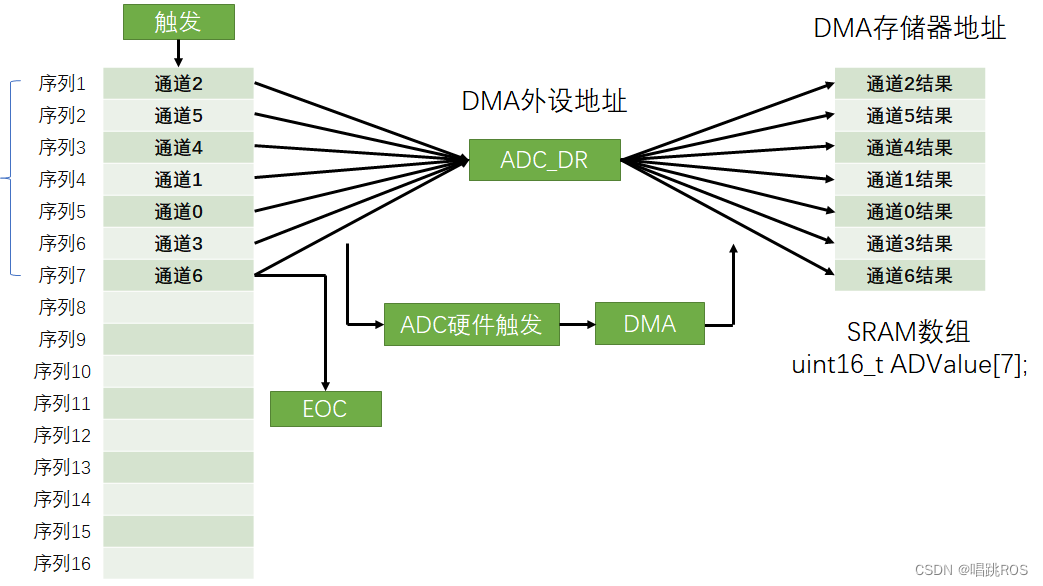
8 DWA(一)
8 DWA DMA简介 DMA(Direct Memory Access)直接存储器存取(可以直接访问32内部存储器,包括内存SRAM,Flash) DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&#x…...

mysql慢查询日志
概念 MySQL的慢查询日志是MySQL提供的一种日志记录,它用来记录在MySQL中响应时间超过阀值的语句,具体指运行时间超过long_query_time值的SQL,则会被记录到慢查询日志中。long_query_time的默认值为10,意思是运行10秒以上的语句。…...
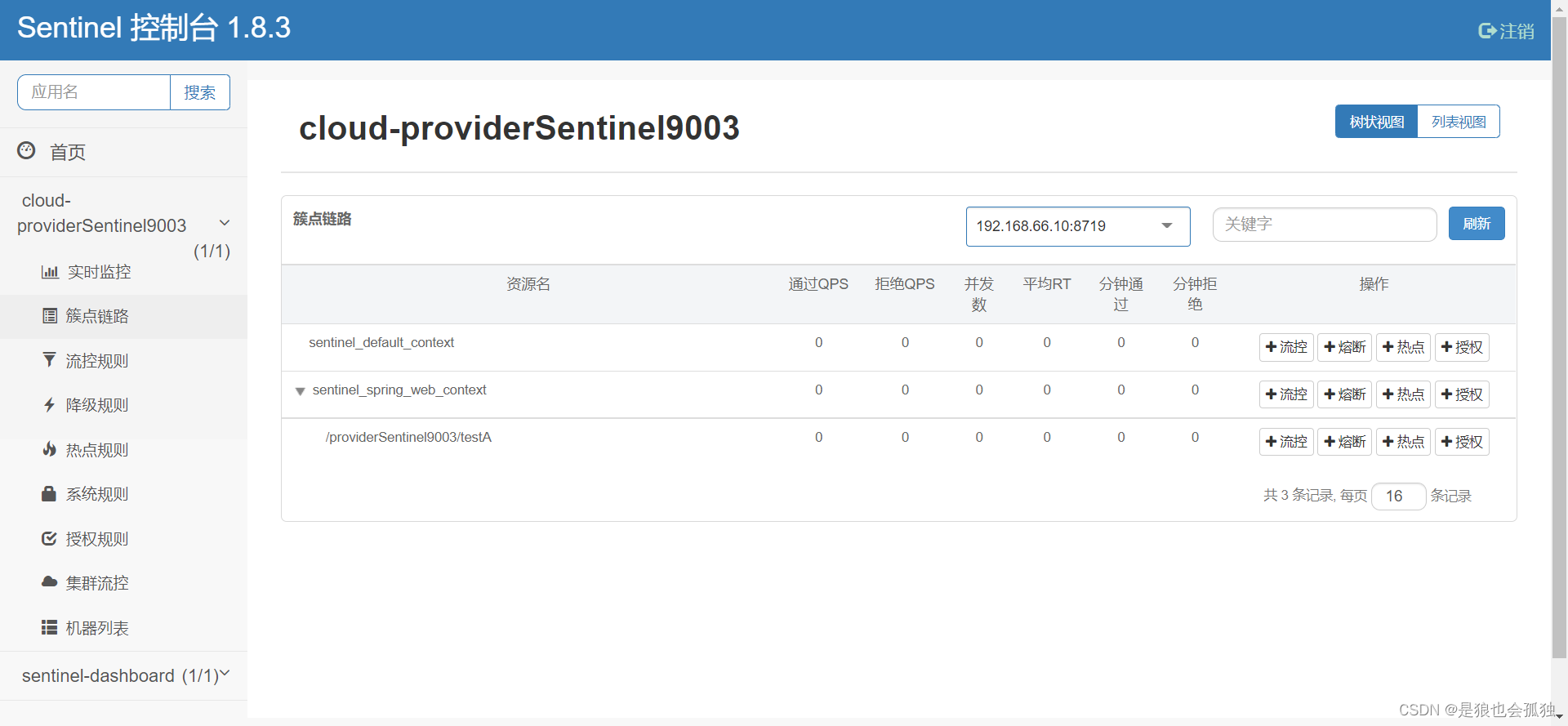
Sentinel介绍及搭建
分布式流量防护 服务雪崩 服务提供者不可用导致服务调用者也跟着不可用,以此类推引起整个链路中的所有微服务都不可用 分布式流量防护 在分布式系统中,服务之间的相互调用会生成分布式流量。如何通过组件进行流量防护,并有效控制流量&…...
最受信任的低代码平台排行榜
近年来,随着数字化转型的兴起,低代码平台获得了大量关注。它允许用户在几乎没有编码知识的情况下创建应用程序,从而使企业能够简化其流程并提高效率。随着低代码平台的日益流行,要确定哪些平台最可靠、最值得信赖并非易事。在本文…...
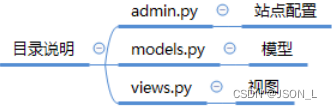
Django框架之创建项目、应用并配置数据库
django3.0框架创建项目、应用并配置数据库 创建项目 进入命令行 新建一个全英文的目录 进入目录 输入命令 django-admin startproject project 项目目录层级 查看当前目录层级 tree /f 目录文件说明 创建数据库 做一个学生管理系统做演示,使用navicat创建数据…...
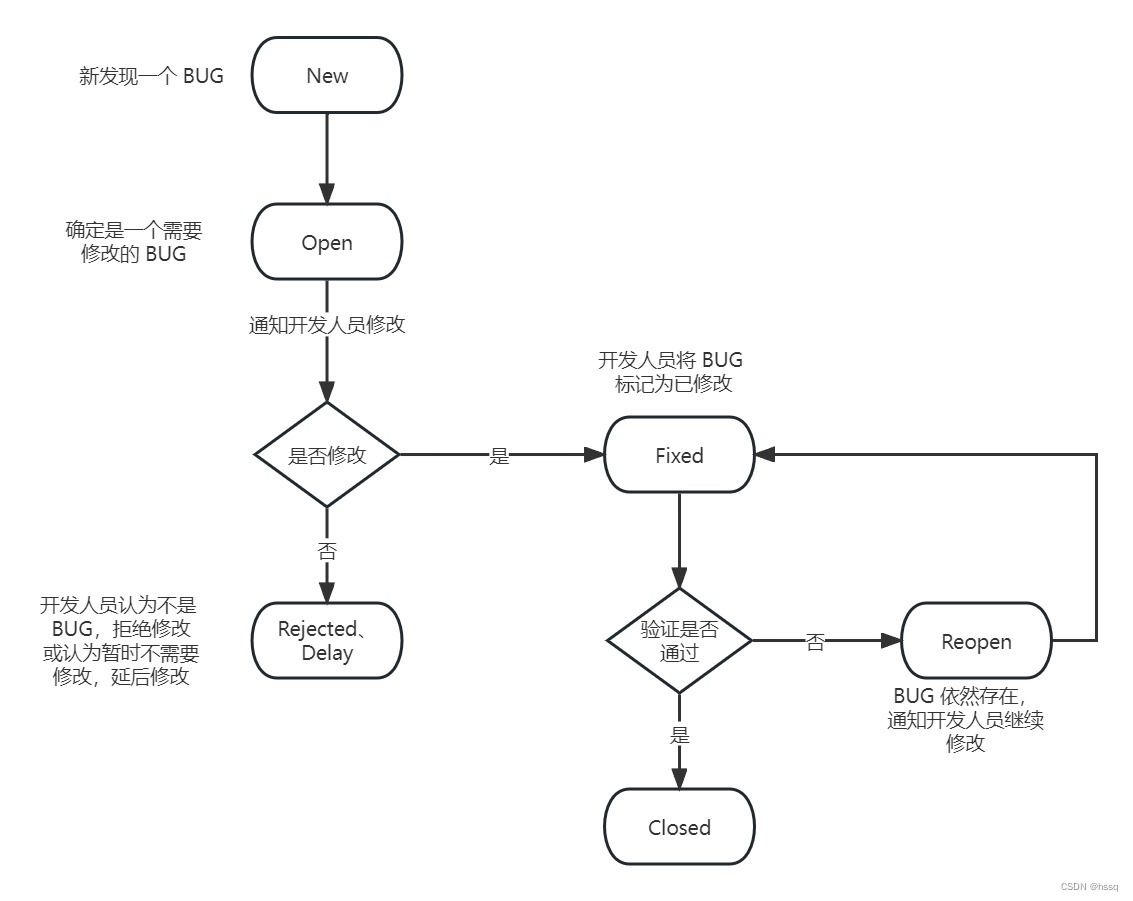
软件测试之基础概念学习篇(需求 + 测试用例 + 开发模型 + 测试模型 + BUG)
文章目录 1. 什么是软件测试2. 软件测试和软件开发的区别3. 软件测试和软件调试的区别4. 什么是需求1)以需求为依据设计测试用例 5. 测试用例是什么6. 什么是 BUG(软件错误)7. 五个开发模型1)瀑布模型2)螺旋模型3&…...
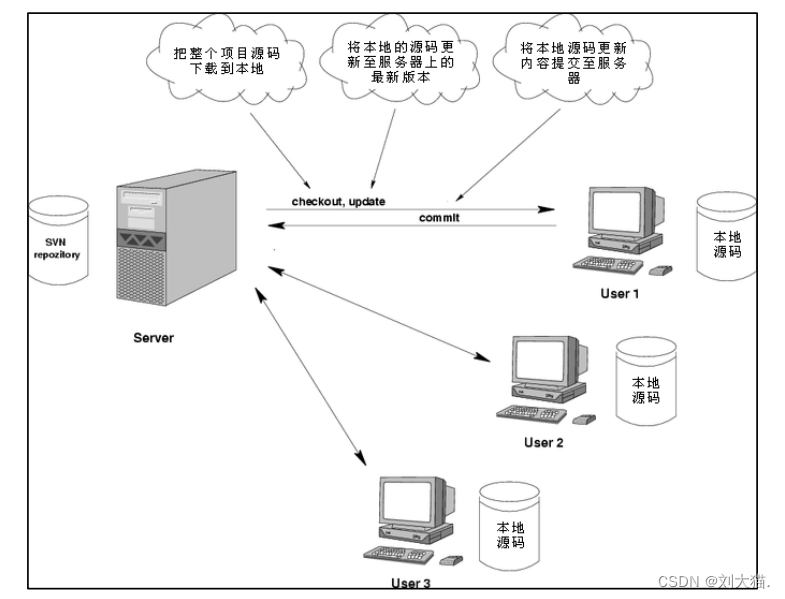
Windows下版本控制器(SVN) - 1、开发中的实际问题+2、版本控制简介
文章目录 基础知识-Windows下版本控制器(SVN)1、开发中的实际问题2、版本控制简介2.1 版本控制[Revision control]2.2 Subversion2.3 Subversion 的优良特性2.4 SVN 的工作原理:2.5 SVN 基本操作 本人其他相关文章链接 基础知识-Windows下版本控制器(SVN) 1、开发中…...

Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记
Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记 摘要 Talking head synthesis is an emerging technology with wide applications in film dubbing, virtual avatars and online education. Recent NeRF-based methods generate more n…...

SpringBoot 项目整合 Redis 教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案
3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案 ABB的机器人解决方案最终选择了IRB6400机器人 ABB的解决方案 ABB一直都在不断地研究和开发机器人应用的新技术,有一部分研究活动是与大学进行合作的,其中一项是ABB的科学家和…...

Java的位运算
目录 1 Java中支持的位运算 2 位运算规则 3 逻辑运算 3.1 与运算(&) 3.2 或运算(|) 3.3 异或运算(^) 3.3 取反运算(~) 4 位移操作 4.1 左移(<<&#…...

FastDFS分布式文件存储
FastDFS文件上传 简介: 主要解决:大容量的文件存储和高并发访问的问题 论坛:https://bbs.chinaunix.net 下载网站:https://sourceforge.net/projects/fastdfs/files/ 安装参考:https://www.cnblogs.com/cxygg/p/1…...

Android的AAC架构
AAC Android Architecture Components的简称,是一套用来搭建具有生命周期感知架构的系列组件,在2017年 GoogleI/O大会上发布。 dependencies {def lifecycle_version "2.2.0"implementation "androidx.lifecycle:lifecycle-livedata-ktx…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
