[Daimayuan] 走不出的迷宫(C++,图论,DP)
有一个 H H H 行 W W W 列的迷宫(行号从上到下是 1 − H 1−H 1−H,列号从左到右是 1 − W 1−W 1−W),现在有一个由 . 和 # 组成的 H 行 W 列的矩阵表示这个迷宫的构造,. 代表可以通过的空地,# 代表不能通过的墙。
现在有个人从 起点 ( 1 , 1 ) (1,1) (1,1) 开始走,他每一步只能往右走一格或者往下走一格,并且他不能跨越迷宫的边界。他会一直走,直到没有可以走的路时停下来。
请问这个人最多可以经过多少个格子?
输入格式
第一行两个整数 H H H, W W W,表示迷宫有 H H H 行 W W W 列。
接下来一个 H H H 行 W W W 列的由 . 和 # 组成的矩阵,表示迷宫的构造。
注意:保证 ( 1 , 1 ) (1,1) (1,1) 的位置一定是 .。
输出格式
一个整数,表示最多步数。
样例输入1
3 4
.#..
..#.
..##
样例输出1
4
样例输入2
1 1
.
样例输出2
1
样例输入3
5 5
.....
.....
.....
.....
.....
样例输出3
9
数据规模
对于全部数据保证 1 ≤ H , W ≤ 100 1≤H,W≤100 1≤H,W≤100
解题思路
主体思路为动态规划,时间复杂度为 O ( H ∗ W ) O(H*W) O(H∗W)。
由题意可知,我们到达一个格子的方式只有从左边和上边到达两种情况,那么我们就继承这两种情况中步数更多的一种 + 1 +1 +1来更新:
sum[i][j] = max(sum[i - 1][j], sum[i][j - 1]) + 1;
采用二重循环遍历整张图,由循环顺序,显而易见:在我们到达(i, j)之前,已经到达了(i - 1, j)和(i, j - 1)。
for (int i = 1; i <= h; i++) {for (int j = 1; j <= w; j++) {sum[i][j] = max(sum[i - 1][j], sum[i][j - 1]) + 1;}
}
但是需要注意两点:
(1)注意障碍物的存在,以下代码采用的方式是掩码把墙的sum置为 0 0 0;
(2)注意寻找最大步数时还需要进行一次 B F S BFS BFS,因为我们可能到达不了某些格子,从而导致我们得到的答案并不是sum数组中的最大值。
AC代码如下:
#include <iostream>
#include <queue>
using namespace std;
const int max_h = 100;
const int max_w = 100;bool map[max_h + 1][max_w + 1], book[max_h][max_w];
long long sum[max_h + 1][max_w + 1];
long long h, w, ans = 1;
struct node { int x, y; };
queue<node>q;inline void read() {string str;cin >> h >> w;for (int i = 1; i <= h; i++) {cin >> str;for (int j = 1; j <= w; j++) {if (str[j - 1] == '.') map[i][j] = true;else map[i][j] = false;}}
}void bfs() {q.push(node{ 1,1 });book[1][1] = true;int step[2][2] = { {1,0}, {0,1} }, temp_x, temp_y;while (!q.empty()) {node temp = q.front(); q.pop();for (int i = 0; i < 2; i++) {temp_x = step[i][0] + temp.x;temp_y = step[i][1] + temp.y;if (temp_x > h || temp_y > w) continue;if (!map[temp_x][temp_y]) continue;if (book[temp_x][temp_y]) continue;q.push(node{ temp_x,temp_y });book[temp_x][temp_y] = true;ans = max(ans, sum[temp_x][temp_y]);}}
}inline void solve() {for (int i = 1; i <= h; i++) {for (int j = 1; j <= h; j++) {sum[i][j] = max(sum[i - 1][j] * map[i - 1][j],sum[i][j - 1] * map[i][j - 1]) + 1;}}bfs();cout << ans << endl;
}int main() {read();solve();return 0;
}相关文章:
)
[Daimayuan] 走不出的迷宫(C++,图论,DP)
有一个 H H H 行 W W W 列的迷宫(行号从上到下是 1 − H 1−H 1−H,列号从左到右是 1 − W 1−W 1−W),现在有一个由 . 和 # 组成的 H 行 W 列的矩阵表示这个迷宫的构造,. 代表可以通过的空地,# 代表不…...

【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
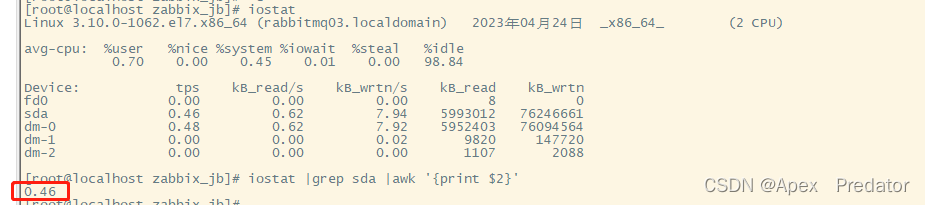
centos7查看磁盘io
1.查看所使用到的命令为iostat,centos7没有自带iostat,需要安装一下 2.安装iostat命令 yum -y install sysstat 3.使用iostat命令 iostat %user:表示用户空间进程使用 CPU 时间的百分比 %nice:表示用户空间进程以降低优先级的…...
浅析低代码开发的典型应用构建场景v
在数字经济蓬勃发展的大势之下,企业软件开发人员供给不足、开发速度慢、开发成本高、数字化和智能化成效不明显等问题日益凸出,阻碍了企业的数字化转型。 而近年来,低代码的出现推动了经济社会的全面提效,也成为人才供求矛盾的润…...
3 连续模块(二)
3.5 零极点增益模块 在控制系统设计和分析中,常用的函数包括 传递函数(tf)、零极点(zpk)和状态空间(ss)函数 传递函数(tf):用于表示线性时不变系统的输入输出…...
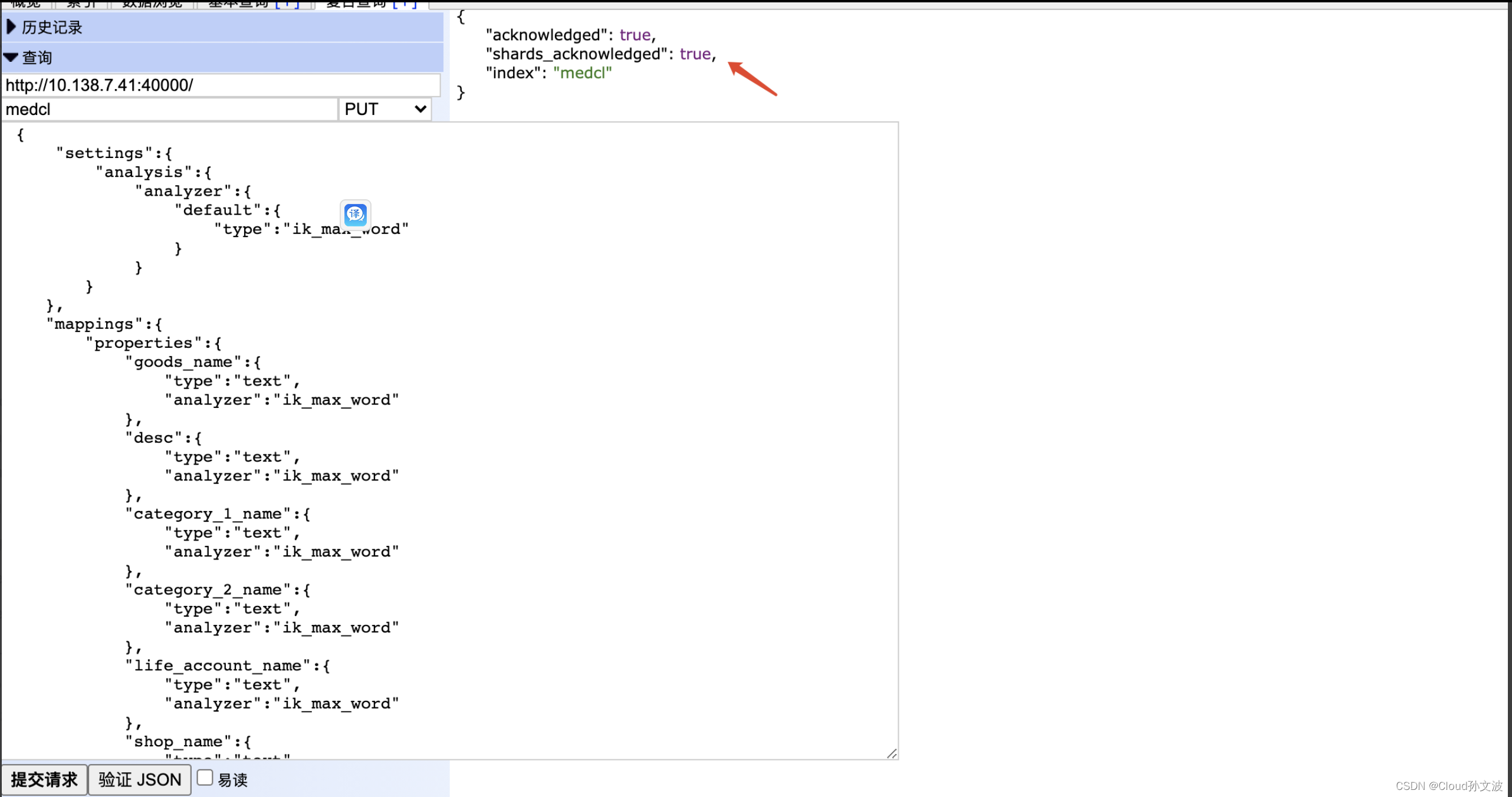
ElasticSearch 部署及安装ik分词器
ansiable playbook链接: https://download.csdn.net/download/weixin_43798031/87719490 需要注意的点:公司es集群现以三个角色部署分别为 Gateway、Master、Data 简单的理解可以理解为在每台机器上部署了三个es,以端口和配置文件来区分这三…...
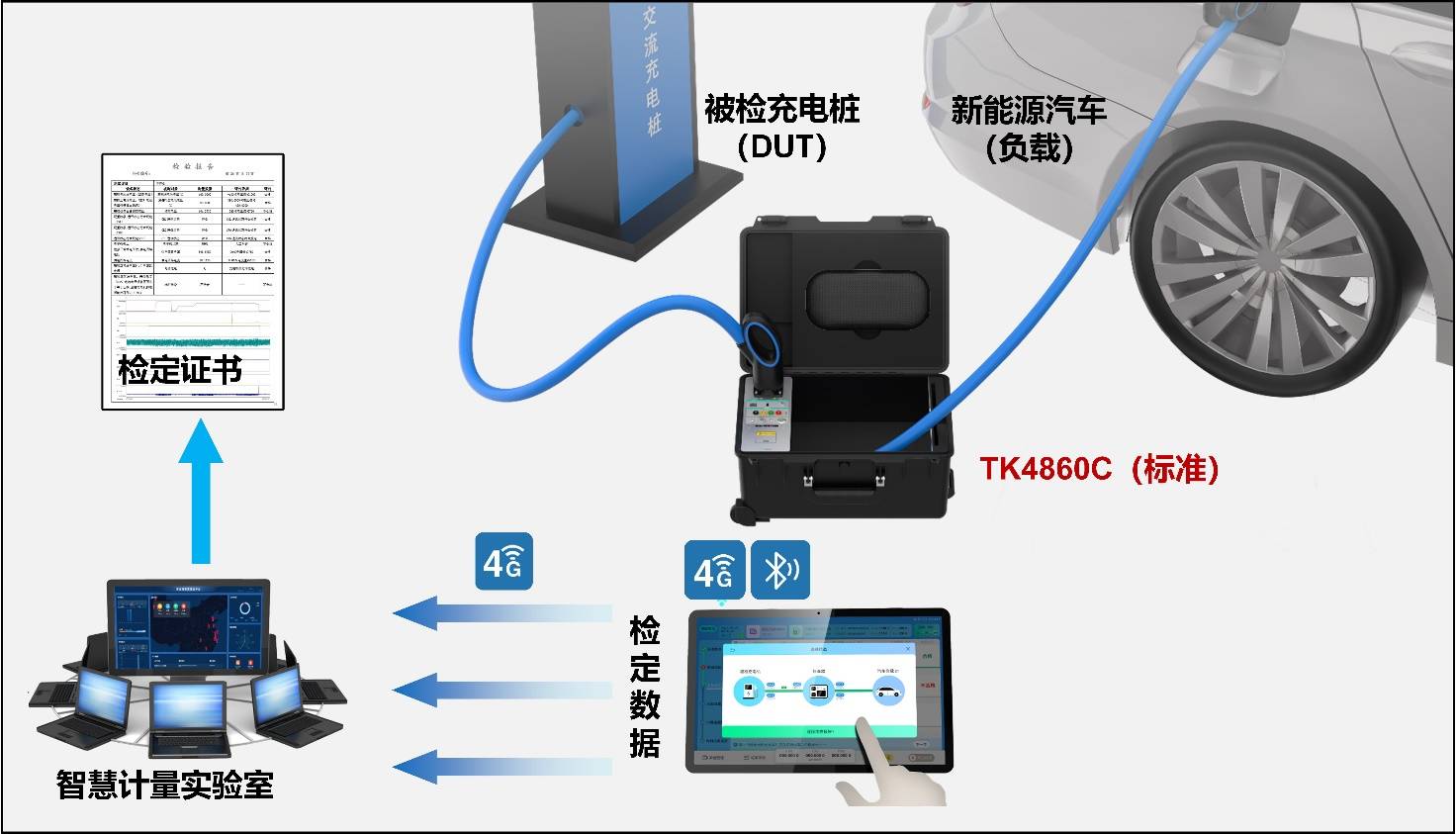
汽车充电桩检测设备TK4860C交流充电桩检定装置
TK4860C是一款在交流充电桩充电过程中实时检测充电电量的标准仪器,仪器以新能源车为负载,结合宽动态范围测量技术、电能ms级高速刷新等技术,TK4860C实现充电全过程的累积电能精准计量,相比于传统的预设检定点的稳态计量࿰…...

备份和恢复:确保数据安全
备份和恢复:确保数据安全 在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。 备份策略概述 在制定备份策略时&…...
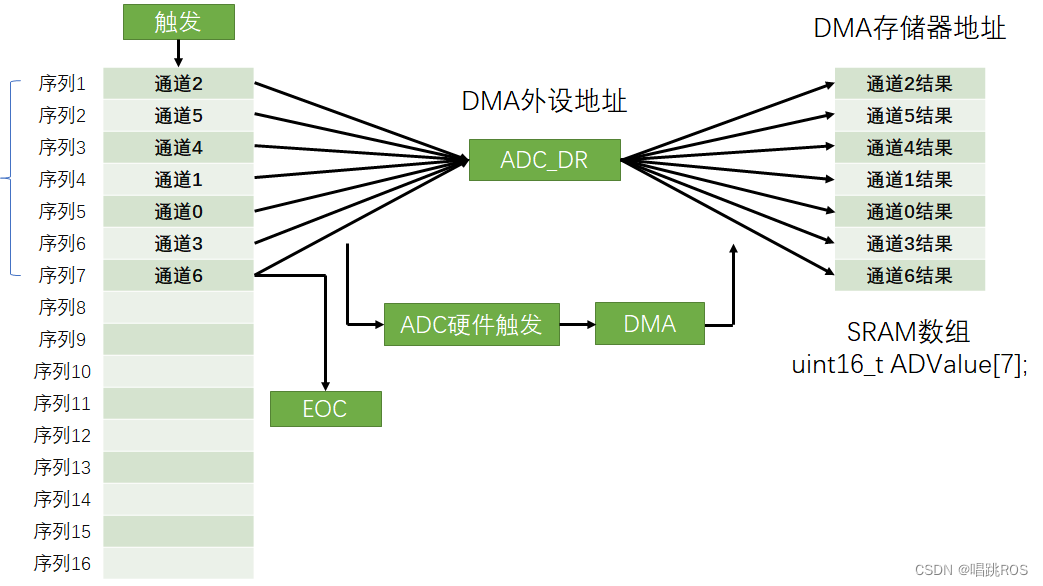
8 DWA(一)
8 DWA DMA简介 DMA(Direct Memory Access)直接存储器存取(可以直接访问32内部存储器,包括内存SRAM,Flash) DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&#x…...

mysql慢查询日志
概念 MySQL的慢查询日志是MySQL提供的一种日志记录,它用来记录在MySQL中响应时间超过阀值的语句,具体指运行时间超过long_query_time值的SQL,则会被记录到慢查询日志中。long_query_time的默认值为10,意思是运行10秒以上的语句。…...
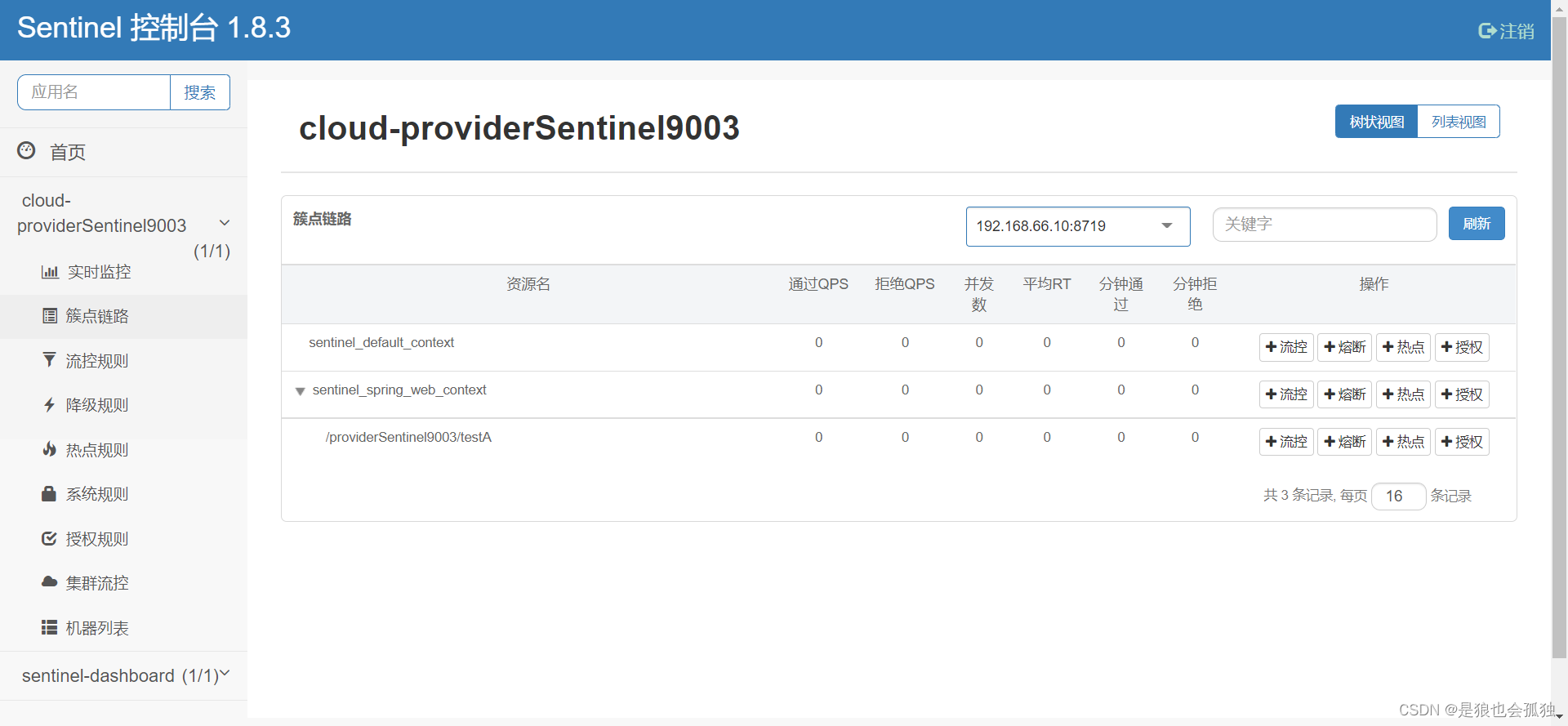
Sentinel介绍及搭建
分布式流量防护 服务雪崩 服务提供者不可用导致服务调用者也跟着不可用,以此类推引起整个链路中的所有微服务都不可用 分布式流量防护 在分布式系统中,服务之间的相互调用会生成分布式流量。如何通过组件进行流量防护,并有效控制流量&…...
最受信任的低代码平台排行榜
近年来,随着数字化转型的兴起,低代码平台获得了大量关注。它允许用户在几乎没有编码知识的情况下创建应用程序,从而使企业能够简化其流程并提高效率。随着低代码平台的日益流行,要确定哪些平台最可靠、最值得信赖并非易事。在本文…...
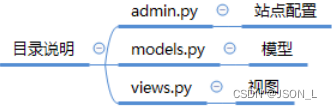
Django框架之创建项目、应用并配置数据库
django3.0框架创建项目、应用并配置数据库 创建项目 进入命令行 新建一个全英文的目录 进入目录 输入命令 django-admin startproject project 项目目录层级 查看当前目录层级 tree /f 目录文件说明 创建数据库 做一个学生管理系统做演示,使用navicat创建数据…...
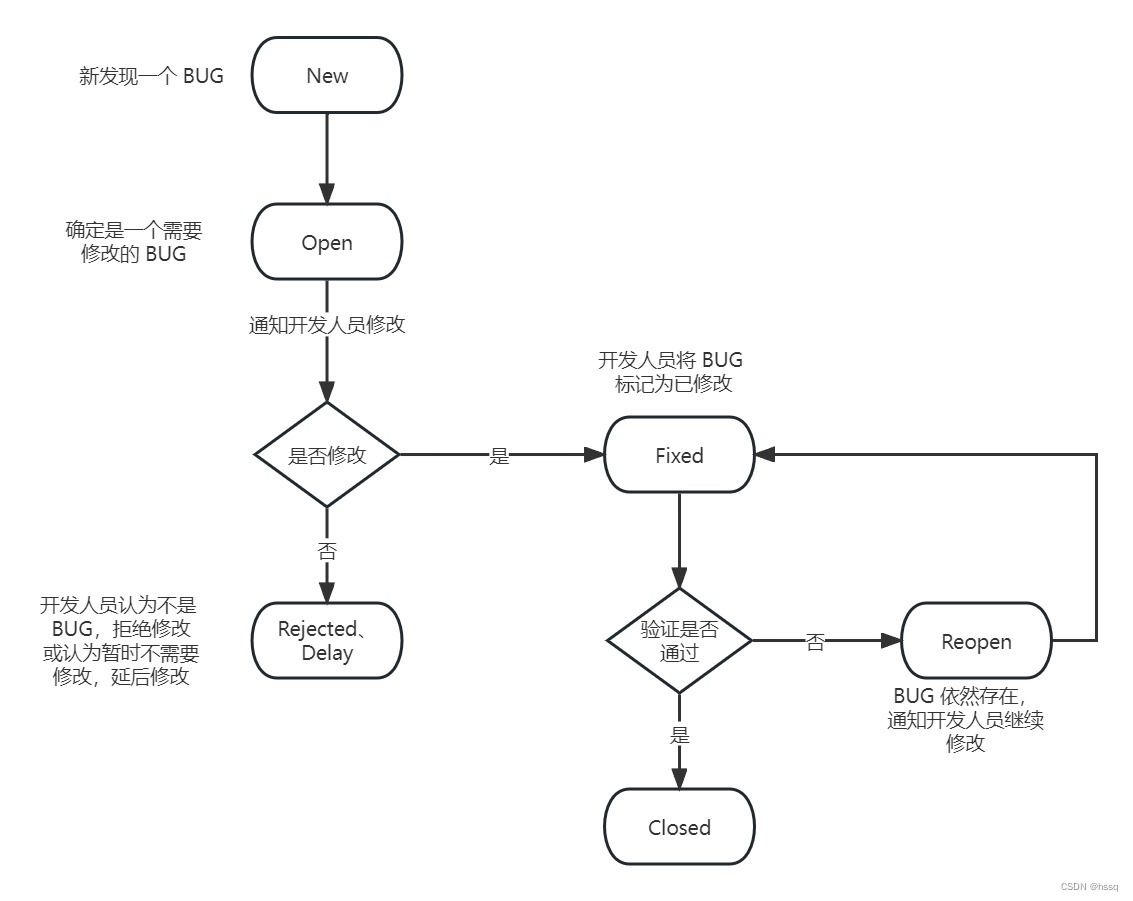
软件测试之基础概念学习篇(需求 + 测试用例 + 开发模型 + 测试模型 + BUG)
文章目录 1. 什么是软件测试2. 软件测试和软件开发的区别3. 软件测试和软件调试的区别4. 什么是需求1)以需求为依据设计测试用例 5. 测试用例是什么6. 什么是 BUG(软件错误)7. 五个开发模型1)瀑布模型2)螺旋模型3&…...
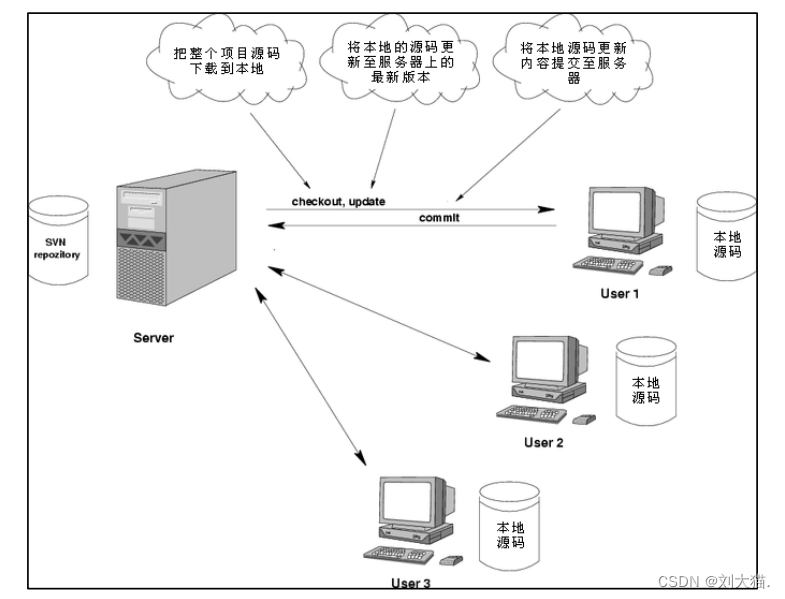
Windows下版本控制器(SVN) - 1、开发中的实际问题+2、版本控制简介
文章目录 基础知识-Windows下版本控制器(SVN)1、开发中的实际问题2、版本控制简介2.1 版本控制[Revision control]2.2 Subversion2.3 Subversion 的优良特性2.4 SVN 的工作原理:2.5 SVN 基本操作 本人其他相关文章链接 基础知识-Windows下版本控制器(SVN) 1、开发中…...

Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记
Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记 摘要 Talking head synthesis is an emerging technology with wide applications in film dubbing, virtual avatars and online education. Recent NeRF-based methods generate more n…...

SpringBoot 项目整合 Redis 教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案
3ASC25H214 DATX130以力控制为基础的装配应用方面已经形成了一个解决方案 ABB的机器人解决方案最终选择了IRB6400机器人 ABB的解决方案 ABB一直都在不断地研究和开发机器人应用的新技术,有一部分研究活动是与大学进行合作的,其中一项是ABB的科学家和…...

Java的位运算
目录 1 Java中支持的位运算 2 位运算规则 3 逻辑运算 3.1 与运算(&) 3.2 或运算(|) 3.3 异或运算(^) 3.3 取反运算(~) 4 位移操作 4.1 左移(<<&#…...

FastDFS分布式文件存储
FastDFS文件上传 简介: 主要解决:大容量的文件存储和高并发访问的问题 论坛:https://bbs.chinaunix.net 下载网站:https://sourceforge.net/projects/fastdfs/files/ 安装参考:https://www.cnblogs.com/cxygg/p/1…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
【JavaEE】万字详解HTTP协议
HTTP是什么?-----互联网的“快递小哥” 想象我们正在网上购物:打开淘宝APP,搜索“蓝牙耳机”,点击商品图片,然后下单付款。这一系列操作背后,其实有一个看不见的“快递小哥”在帮我们传递信息,…...

设计模式-3 行为型模式
一、观察者模式 1、定义 定义对象之间的一对多的依赖关系,这样当一个对象改变状态时,它的所有依赖项都会自动得到通知和更新。 描述复杂的流程控制 描述多个类或者对象之间怎样互相协作共同完成单个对象都无法单独度完成的任务 它涉及算法与对象间职责…...
