CF914G Sum the Fibonacci
CF914G Sum the Fibonacci
洛谷Sum the Fibonacci
题目大意
给你一个长度为 n n n的数组 s s s,定义五元组 ( a , b , c , d , e ) (a,b,c,d,e) (a,b,c,d,e)是合法的当且仅当:
- 1 ≤ a , b , c , d , e ≤ n 1\leq a,b,c,d,e\leq n 1≤a,b,c,d,e≤n
- ( s a ∣ s b ) & s c & ( s d ⊕ s e ) = 2 i , i ∈ Z (s_a|s_b)\& s_c\& (s_d\oplus s_e)=2^i,i\in Z (sa∣sb)&sc&(sd⊕se)=2i,i∈Z
- s a & s b = 0 s_a\& s_b=0 sa&sb=0
对于所有合法的五元组 ( a , b , c , d , e ) (a,b,c,d,e) (a,b,c,d,e),求 ∑ f ( s a ∣ s b ) × f ( s c ) × f ( s d ⊕ s e ) \sum f(s_a|s_b)\times f(s_c)\times f(s_d\oplus s_e) ∑f(sa∣sb)×f(sc)×f(sd⊕se)
f 0 = 0 , f 1 = 1 , f i = f i − 1 + f i − 2 ( i ≥ 2 ) f_0=0,f_1=1,f_i=f_{i-1}+f_{i-2}(i\geq 2) f0=0,f1=1,fi=fi−1+fi−2(i≥2)
输出答案对 1 0 9 + 7 10^9+7 109+7取模后的值。
1 ≤ n ≤ 1 0 6 , 0 ≤ s i < 2 17 1\leq n\leq 10^6,0\leq s_i<2^{17} 1≤n≤106,0≤si<217
题解
令 i = s a & s b , j = s c , k = s d ⊕ s e i=s_a\&s_b,j=s_c,k=s_d\oplus s_e i=sa&sb,j=sc,k=sd⊕se
题意即求
∑ p ∑ i & j & k = 2 p f i × f j × f k × ( ∑ s a ∣ s b = i , s a & s b = 0 1 ) × ( ∑ s c = j 1 ) × ( ∑ s d ⊕ s e = k 1 ) \sum\limits_p\sum\limits_{i\& j\& k=2^p}f_i\times f_j\times f_k\times (\sum\limits_{s_a|s_b=i,s_a\& s_b=0}1)\times (\sum\limits_{s_c=j}1)\times (\sum\limits_{s_d\oplus s_e=k}1) p∑i&j&k=2p∑fi×fj×fk×(sa∣sb=i,sa&sb=0∑1)×(sc=j∑1)×(sd⊕se=k∑1)
令 p i p_i pi表示 i i i在数组 s s s中出现的次数,那么
( ∑ s a ∣ s b = i , s a & s b = 0 1 ) = ∑ x ∣ y = i , x & y = 0 p x × p y (\sum\limits_{s_a|s_b=i,s_a\& s_b=0}1)=\sum\limits_{x|y=i,x\& y=0}p_x\times p_y (sa∣sb=i,sa&sb=0∑1)=x∣y=i,x&y=0∑px×py
( ∑ s c = j 1 ) = p j (\sum\limits_{s_c=j}1)=p_j (sc=j∑1)=pj
( ∑ s d ⊕ s e = k 1 ) = ∑ i ⊕ j = k p i × p j (\sum\limits_{s_d\oplus s_e=k}1)=\sum\limits_{i\oplus j=k}p_i\times p_j (sd⊕se=k∑1)=i⊕j=k∑pi×pj
第二个式子很好求。对于第一个式子和第三个式子,用 F W T FWT FWT的子集卷积和异或卷积,分别用 O ( m log 2 m ) , O ( m log m ) O(m\log^2 m),O(m\log m) O(mlog2m),O(mlogm)的时间复杂度求出,其中 m = 2 17 m=2^{17} m=217。
code
#include<bits/stdc++.h>
using namespace std;
int n,x,cnt[1<<17];
long long ans=0,f[1<<17],s[1<<17],t[20][1<<17],a[1<<17],b[1<<17],c[1<<17],v[1<<17];
const long long mod=1e9+7,ny2=5e8+4;
void pt(long long *w){for(int i=0;i<1<<17;i++) w[i]=s[i];
}
void fwt_or(long long *w,int fl){for(int s=2;s<=1<<17;s<<=1){int mid=s>>1;for(int v=0;v<1<<17;v+=s){for(int i=0;i<mid;i++){w[v+mid+i]=(w[v+mid+i]+fl*w[v+i]+mod)%mod;}}}
}
void fwt_and(long long *w,int fl){for(int s=2;s<=1<<17;s<<=1){int mid=s>>1;for(int v=0;v<1<<17;v+=s){for(int i=0;i<mid;i++){w[v+i]=(w[v+i]+fl*w[v+mid+i]+mod)%mod;}}}
}
void fwt_xor(long long *w,int fl){for(int s=2;s<=1<<17;s<<=1){int mid=s>>1;for(int v=0;v<1<<17;v+=s){for(int i=0;i<mid;i++){long long t1=w[v+i],t2=w[v+mid+i];w[v+i]=(t1+t2)%mod;w[v+mid+i]=(t1-t2+mod)%mod;if(fl==-1){w[v+i]=w[v+i]*ny2%mod;w[v+mid+i]=w[v+mid+i]*ny2%mod;}}}}
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&x);++s[x];}f[0]=0;f[1]=1;cnt[1]=1;for(int i=2;i<1<<17;i++){cnt[i]=cnt[i-(i&(-i))]+1;f[i]=(f[i-1]+f[i-2])%mod;}for(int i=0;i<1<<17;i++){t[cnt[i]][i]=s[i];}for(int i=0;i<=17;i++){fwt_or(t[i],1);}for(int i=0;i<=17;i++){for(int j=0;j<=i;j++){for(int k=0;k<1<<17;k++){v[k]=(v[k]+t[j][k]*t[i-j][k]%mod)%mod;}}fwt_or(v,-1);for(int j=0;j<(1<<17);j++){if(cnt[j]==i) a[j]=v[j];v[j]=0;}}pt(b);pt(c);fwt_xor(c,1);for(int i=0;i<1<<17;i++){c[i]=c[i]*c[i]%mod;}fwt_xor(c,-1);for(int i=0;i<1<<17;i++){a[i]=a[i]*f[i]%mod;b[i]=b[i]*f[i]%mod;c[i]=c[i]*f[i]%mod;}fwt_and(a,1);fwt_and(b,1);fwt_and(c,1);for(int i=0;i<1<<17;i++){v[i]=a[i]*b[i]%mod*c[i]%mod;}fwt_and(v,-1);for(int i=1;i<1<<17;i<<=1){ans=(ans+v[i])%mod;}printf("%lld",ans);return 0;
}
相关文章:

CF914G Sum the Fibonacci
CF914G Sum the Fibonacci 洛谷Sum the Fibonacci 题目大意 给你一个长度为 n n n的数组 s s s,定义五元组 ( a , b , c , d , e ) (a,b,c,d,e) (a,b,c,d,e)是合法的当且仅当: 1 ≤ a , b , c , d , e ≤ n 1\leq a,b,c,d,e\leq n 1≤a,b,c,d,e≤n ( …...

Shell基础入门实战
写在前面 好久没在项目内做自动化了,主要是现阶段在项目内做自动化收益不大,最近开发做batch run的正好缺人,我看了一下代码,就是通过代码读取jar包和远程服务器连接,然后通过shell脚本,向数据库插入数据&a…...
如何进行微服务的技术选型?
本文首发自「慕课网」,想了解更多IT干货内容,程序员圈内热闻,欢迎关注"慕课网"! 作者:陈于吉吉|慕课网讲师 随着这几年微服务的火爆,在平时的工作或者技术交流中,我们总能听到哪家公…...
Vue电商项目--应用开发详解
vue-cli脚手架初始化项目 首先,页面上新建一个文件夹。然后打开命令端口 vue create app 选择Default ([Vue 2] babel, eslint) 然后把项目拖拽到vscode中。项目目录看一下 脚手架项目的目录 node_modules:放置项目依赖的地方 public:一般放置一些共用的静态资源&a…...
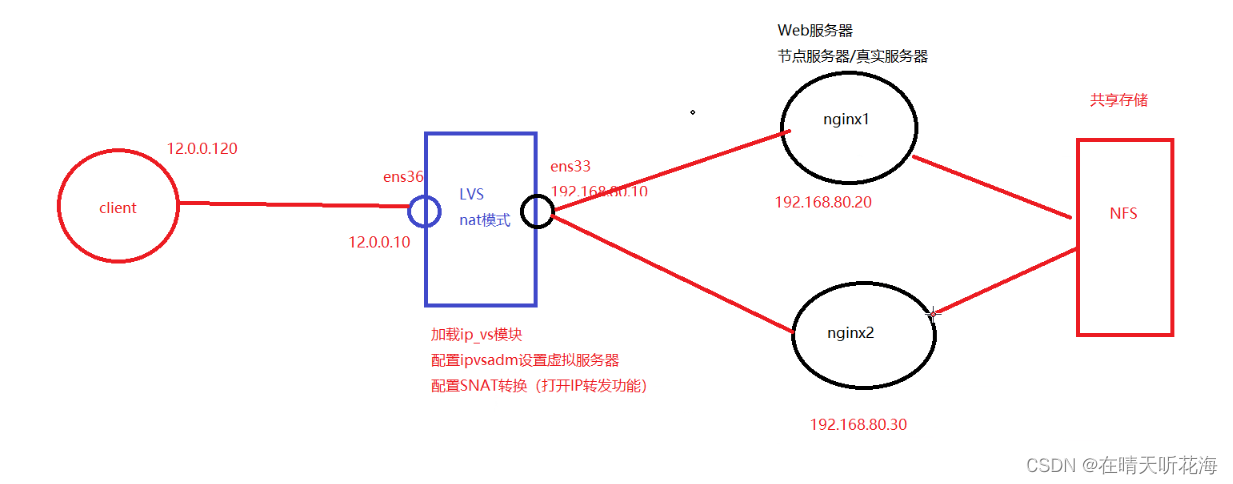
Lvs负载均衡
系列文章目录 文章目录 系列文章目录一、集群1.集群2. 二、LVS1.LVS简介2.负载均衡的结构3.Lvs调度算法 总结 一、集群 1.集群 集群群集 cluster由多台主机构成的一个整体,提供一个放问入口(IP或域名),集群中的多台主机都干一件事提供一样的服务 负载均…...

JAVAWeb08-手动实现 Tomcat 底层机制+ 自己设计 Servlet
1. 前言 先看一个小案例, 引出对 Tomcat 底层实现思考 1.1 完成小案例 ● 快速给小伙伴完成这个小案例 0. 我们准备使用 Maven 来创建一个 WEB 项目, 老师先简单给小伙伴介绍一下 Maven 是什么, 更加详细的使用,我们还会细讲, 现在先使用一把 先创建…...

非监督学习简单介绍
文章目录 非监督学习简单介绍聚类K-meansHierarchical聚类DBSCAN 降维PCAt-SNE 其他非监督学习技术结论 非监督学习简单介绍 非监督学习是机器学习中的一种方法,其目标是基于数据的内在结构和关系,从而在无标签数据中识别样本的潜在结构和模式。非监督学…...

香港科技大学有什么好的专业?
香港科技大学创办于1991年10月,是一所坐落于香港清水湾半岛的公立研究型大学。大学设有4个学院:工学院、理学院、人文社会科学学院和工商管理学院,还设有2个研究院:香港科技大学公共政策和行政研究生院和香港科技大学霍英东研究院…...

【两个月算法速成】day04
本文以收录专题刷题记录 目录 24. 两两交换链表中的节点 题目链接 思路 代码 19. 删除链表的倒数第 N 个结点 题目链接 思路-双指针 代码 面试题 02.07. 链表相交 题目链接 思路 代码 24. 两两交换链表中的节点 题目链接 力扣 思路 建议使用虚拟节点࿰…...
【Python】实战:生成无关联单选问卷 csv《压疮风险评估表》
目录 一、适用场景 二、业务需求 三、Python 文件 (1)创建文件 (2)代码示例 四、csv 文件 一、适用场景 实战场景: 问卷全部为单选题问卷问题全部为必填问题之间无关联关系每个问题的答案分数不同根据问卷全部问…...

rsync 远程删除文件
rsync 远程删除文件 rsync是一个强大的远程数据同步工具,它不仅可以实现远程文件复制,也可以实现远程文件删除。 要使用rsync实现远程删除文件,可以使用如下命令: bash rsync -avz --delete usernameremotehost:/path/to/files /path/to/local/dir这个命令的主要参数: -a:归…...

LinkedBlockingQueue原理
1. 基本的入队出队 public class LinkedBlockingQueue<E> extends AbstractQueue<E>implements BlockingQueue<E>, java.io.Serializable {static class Node<E> {E item;/*** 下列三种情况之一* - 真正的后继节点* - 自己, 发生在出队时* - null, 表…...
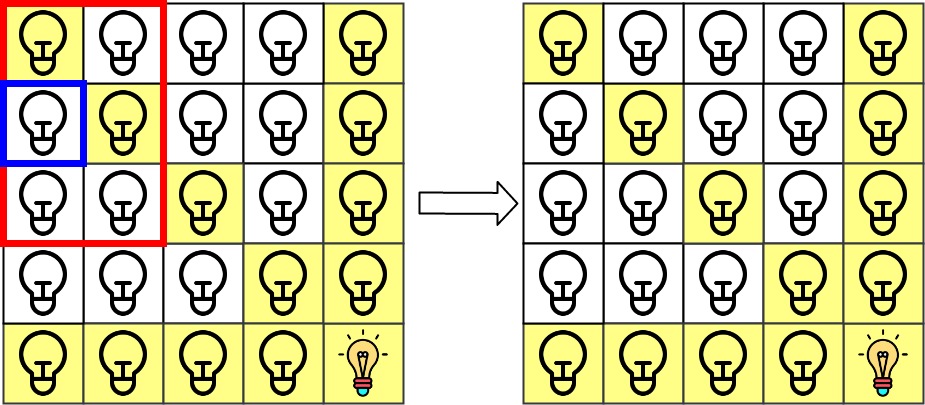
哈希表题目:网格照明
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:网格照明 出处:1001. 网格照明 难度 6 级 题目描述 要求 在 n n \texttt{n} \times \texttt{n} nn 的二维网格 grid \texttt{grid}…...

Python多线程爬虫为何效率低下?解析原因并提高爬虫速度的方法
目录 一、知识点二、多线程语法GIL单线程多线程单线程多线程 最后的惊喜 一、知识点 线程(Thread)也叫轻量级进程,是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。线程自己不拥有…...
)
Python 标准方形信号定义(完美实现)
之前我们介绍了如何定义一个标准的正弦信号,这里我们做一下延申,简单说明一下如何定义一个方形函数。 方形信号表达式 square signal = g ( t ) = sign [ sin ( 2 π f t +...
)
[Daimayuan] 走不出的迷宫(C++,图论,DP)
有一个 H H H 行 W W W 列的迷宫(行号从上到下是 1 − H 1−H 1−H,列号从左到右是 1 − W 1−W 1−W),现在有一个由 . 和 # 组成的 H 行 W 列的矩阵表示这个迷宫的构造,. 代表可以通过的空地,# 代表不…...

【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
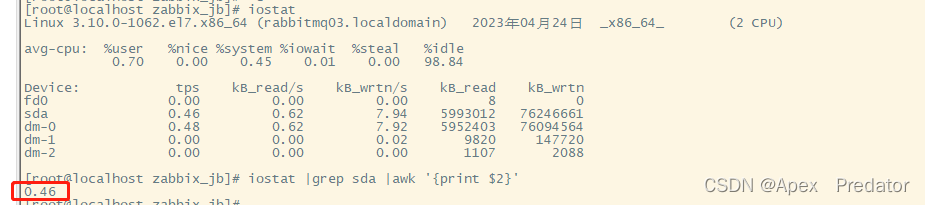
centos7查看磁盘io
1.查看所使用到的命令为iostat,centos7没有自带iostat,需要安装一下 2.安装iostat命令 yum -y install sysstat 3.使用iostat命令 iostat %user:表示用户空间进程使用 CPU 时间的百分比 %nice:表示用户空间进程以降低优先级的…...
浅析低代码开发的典型应用构建场景v
在数字经济蓬勃发展的大势之下,企业软件开发人员供给不足、开发速度慢、开发成本高、数字化和智能化成效不明显等问题日益凸出,阻碍了企业的数字化转型。 而近年来,低代码的出现推动了经济社会的全面提效,也成为人才供求矛盾的润…...
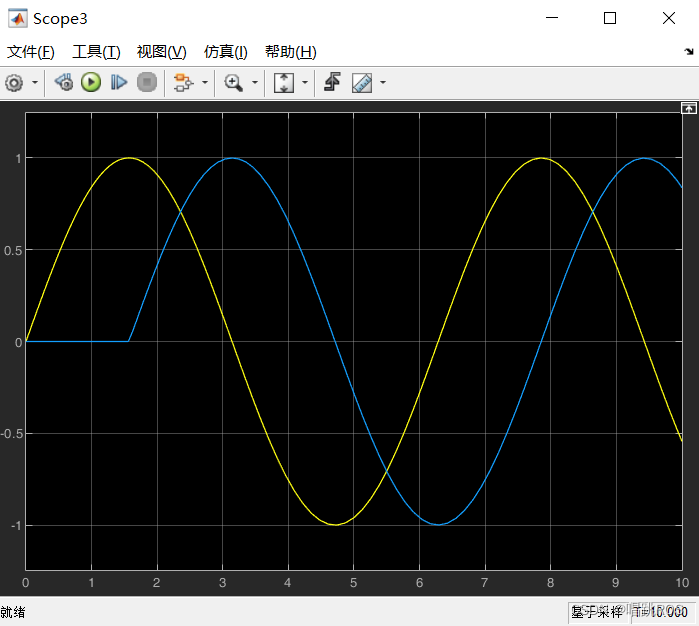
3 连续模块(二)
3.5 零极点增益模块 在控制系统设计和分析中,常用的函数包括 传递函数(tf)、零极点(zpk)和状态空间(ss)函数 传递函数(tf):用于表示线性时不变系统的输入输出…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
