非监督学习简单介绍
文章目录
- 非监督学习简单介绍
- 聚类
- K-means
- Hierarchical聚类
- DBSCAN
- 降维
- PCA
- t-SNE
- 其他非监督学习技术
- 结论
非监督学习简单介绍
非监督学习是机器学习中的一种方法,其目标是基于数据的内在结构和关系,从而在无标签数据中识别样本的潜在结构和模式。非监督学习的目的是发现未知结构,无需使用任何预先定义的目标变量,这与监督学习的目标相反。
非监督学习的主要方法包括聚类、降维等技术。
聚类
聚类是一种非监督学习方法,它将给定的数据集中的样本分成不同的组或簇,每个簇包含相似的数据点。聚类可以帮助我们在数据集中发现潜在的模式和结构,从而加深对数据集的理解。
聚类是非监督学习中最常见的方法之一,其目的是将数据集中的观测样本分组或者簇。 对于同一簇中的样本尽可能的相似,而不同簇之间的样本则相差较大。
常用的聚类算法包括 K-means、Hierarchical聚类和DBSCAN。
K-means
K-means算法是一种最简单和流行的聚类算法,其工作原理如下:
- 首先,选择需要分组的数量(即簇数k)。
- 随机选择k个样本点作为聚类中心。
- 将所有的样本点分配到距离最近的聚类中心。
- 更新每个簇的聚类中心位置。
- 重复运行步骤3和4,直到满足收敛条件为止。
代码实现:
from sklearn.cluster import KMeans
import numpy as np# 数据集
X = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52], [80, 91]])
plt.scatter(x[:,0],x[:,1], s = 50)
plt.show()# 聚类数,使用K-Means算法对数据进行聚类
kmeans = KMeans(n_clusters=2)# 训练模型
kmeans.fit(X)# 可视化聚类效果
plt.scatter(x[:,0],x[:,1], c = kmeans.labels_, s=50)
plt.show()# 打印聚类中心
print(kmeans.cluster_centers_)# 预测簇
print(kmeans.labels_)
Hierarchical聚类
层次聚类也叫分级聚类,可以是自下向上或自上而下的方法,利用不同的相似度度量来生成一棵树形的层次结构。
代码实现:
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
import numpy as np# 数据集
X = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52], [80, 91]])# 层次聚类
linked = linkage(X, 'single')# 绘制谱系树
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top', distance_sort='descending', show_leaf_counts=True)
plt.show()
DBSCAN
DBSCAN算法确定簇的数量而不是预设定好的。该算法将一个给定的数据集划分到不同的簇中。对于每个簇,它的形状可以是任意形状。除此之外,该算法还能识别出噪声数据点。
代码实现:
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt# 数据集
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)# DBSCAN聚类
dbscan = DBSCAN(eps=0.2, min_samples=5)
clusters = dbscan.fit_predict(X)# 绘图聚类
plt.scatter(X[:, 0], X[:, 1], c=clusters, s=50, cmap='viridis');
plt.show()
以上代码首先生成了一个包含6个数据点的人工数据集,并将其可视化。然后,使用K-Means算法将数据分成两类,并将聚类结果可视化。
降维
降维也是非监督学习中非常重要的一部分,其目标是将高维数据映射到低维空间。 降维可以帮助我们更好地理解数据,同时还能减少特征的数量,这样也就使得机器学习算法的计算量更小,从而更快地训练模型。
常用的降维算法包括PCA和t-SNE。
PCA
PCA(主成分分析)是一种将高维数据转换为低维数据的线性算法。它通过找到数据中主要的变化方向,创建新的低维特征。
代码实现:
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt# 数据集
iris = load_iris()
X = iris.data
y = iris.target# 可视化数据
plt.scatter(x[:0],x[:,1],c = y, s = 50)
plt.show()# PCA分析,使用pca算法降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)# 绘制结果
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, s=50, cmap='viridis')
plt.show()
t-SNE
t-SNE(t-Distributed Stochastic Neighbor Embedding)是目前最流行的非线性降维算法之一。 它能够将高维数据点映射到低维空间,并尽可能保留高维数据点之间的局部结构。
代码实现:
from sklearn.datasets import load_digits
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import seaborn as sns# 数据集
digits = load_digits()
X = digits.data
y = digits.target# t-SNE分析
tsne = TSNE(n_components=2, perplexity=30, verbose=2)
X_tsne = tsne.fit_transform(X)# 绘制结果
plt.figure(figsize=(10, 10))
sns.scatterplot(X_tsne[:, 0], X_tsne[:, 1], hue=y, legend='full', palette='Spectral')
plt.title('t-SNE')
plt.show()
其他非监督学习技术
除了聚类和降维算法外,还有许多其他非监督学习技术,如异常检测、关联规则、深度学习自编码器等。 它们的应用场景各不相同,可以根据需要选择合适的技术。
结论
本教程介绍了非监督学习中最常见的聚类和降维算法,以及其他一些非监督学习技术。 相信读者对非监督学习有了更深入的了解,并能够将其应用到实际的问题中去。
相关文章:

非监督学习简单介绍
文章目录 非监督学习简单介绍聚类K-meansHierarchical聚类DBSCAN 降维PCAt-SNE 其他非监督学习技术结论 非监督学习简单介绍 非监督学习是机器学习中的一种方法,其目标是基于数据的内在结构和关系,从而在无标签数据中识别样本的潜在结构和模式。非监督学…...

香港科技大学有什么好的专业?
香港科技大学创办于1991年10月,是一所坐落于香港清水湾半岛的公立研究型大学。大学设有4个学院:工学院、理学院、人文社会科学学院和工商管理学院,还设有2个研究院:香港科技大学公共政策和行政研究生院和香港科技大学霍英东研究院…...

【两个月算法速成】day04
本文以收录专题刷题记录 目录 24. 两两交换链表中的节点 题目链接 思路 代码 19. 删除链表的倒数第 N 个结点 题目链接 思路-双指针 代码 面试题 02.07. 链表相交 题目链接 思路 代码 24. 两两交换链表中的节点 题目链接 力扣 思路 建议使用虚拟节点࿰…...
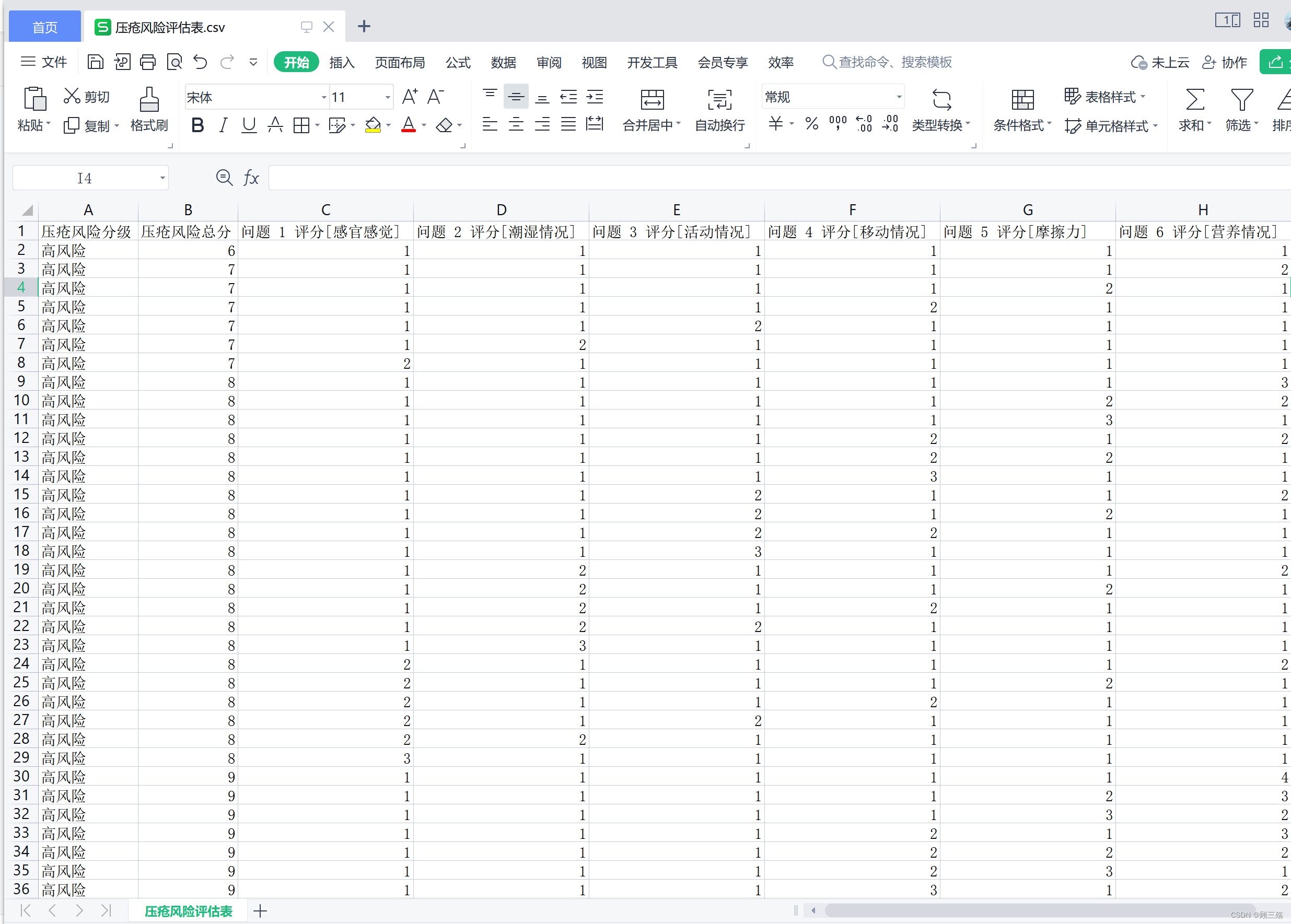
【Python】实战:生成无关联单选问卷 csv《压疮风险评估表》
目录 一、适用场景 二、业务需求 三、Python 文件 (1)创建文件 (2)代码示例 四、csv 文件 一、适用场景 实战场景: 问卷全部为单选题问卷问题全部为必填问题之间无关联关系每个问题的答案分数不同根据问卷全部问…...

rsync 远程删除文件
rsync 远程删除文件 rsync是一个强大的远程数据同步工具,它不仅可以实现远程文件复制,也可以实现远程文件删除。 要使用rsync实现远程删除文件,可以使用如下命令: bash rsync -avz --delete usernameremotehost:/path/to/files /path/to/local/dir这个命令的主要参数: -a:归…...

LinkedBlockingQueue原理
1. 基本的入队出队 public class LinkedBlockingQueue<E> extends AbstractQueue<E>implements BlockingQueue<E>, java.io.Serializable {static class Node<E> {E item;/*** 下列三种情况之一* - 真正的后继节点* - 自己, 发生在出队时* - null, 表…...
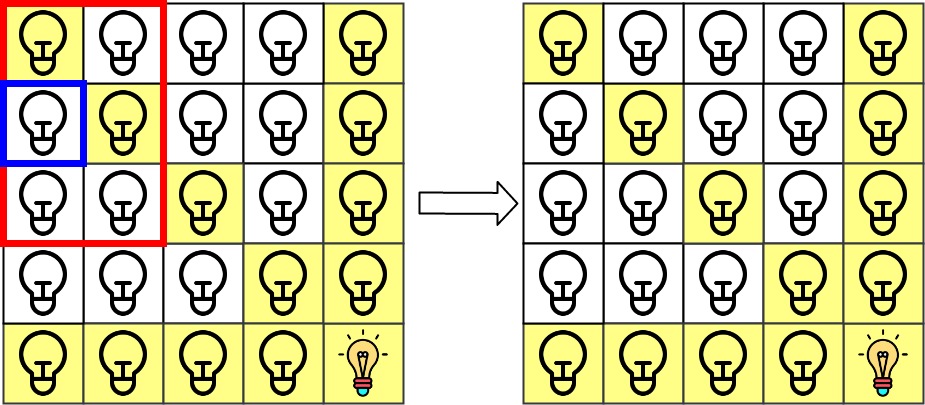
哈希表题目:网格照明
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:网格照明 出处:1001. 网格照明 难度 6 级 题目描述 要求 在 n n \texttt{n} \times \texttt{n} nn 的二维网格 grid \texttt{grid}…...

Python多线程爬虫为何效率低下?解析原因并提高爬虫速度的方法
目录 一、知识点二、多线程语法GIL单线程多线程单线程多线程 最后的惊喜 一、知识点 线程(Thread)也叫轻量级进程,是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。线程自己不拥有…...
)
Python 标准方形信号定义(完美实现)
之前我们介绍了如何定义一个标准的正弦信号,这里我们做一下延申,简单说明一下如何定义一个方形函数。 方形信号表达式 square signal = g ( t ) = sign [ sin ( 2 π f t +...
)
[Daimayuan] 走不出的迷宫(C++,图论,DP)
有一个 H H H 行 W W W 列的迷宫(行号从上到下是 1 − H 1−H 1−H,列号从左到右是 1 − W 1−W 1−W),现在有一个由 . 和 # 组成的 H 行 W 列的矩阵表示这个迷宫的构造,. 代表可以通过的空地,# 代表不…...

【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
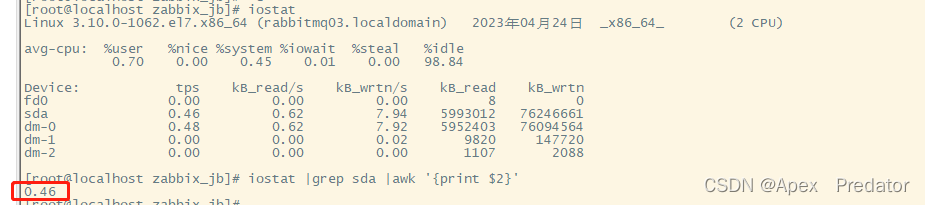
centos7查看磁盘io
1.查看所使用到的命令为iostat,centos7没有自带iostat,需要安装一下 2.安装iostat命令 yum -y install sysstat 3.使用iostat命令 iostat %user:表示用户空间进程使用 CPU 时间的百分比 %nice:表示用户空间进程以降低优先级的…...
浅析低代码开发的典型应用构建场景v
在数字经济蓬勃发展的大势之下,企业软件开发人员供给不足、开发速度慢、开发成本高、数字化和智能化成效不明显等问题日益凸出,阻碍了企业的数字化转型。 而近年来,低代码的出现推动了经济社会的全面提效,也成为人才供求矛盾的润…...
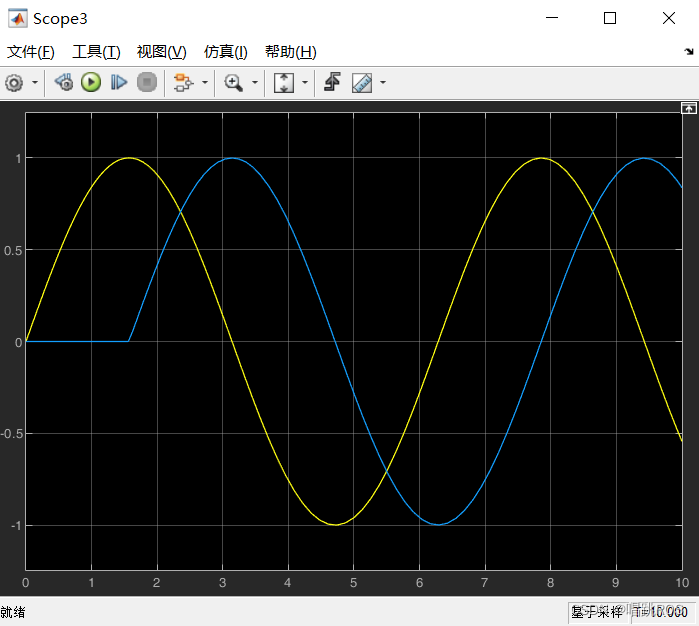
3 连续模块(二)
3.5 零极点增益模块 在控制系统设计和分析中,常用的函数包括 传递函数(tf)、零极点(zpk)和状态空间(ss)函数 传递函数(tf):用于表示线性时不变系统的输入输出…...
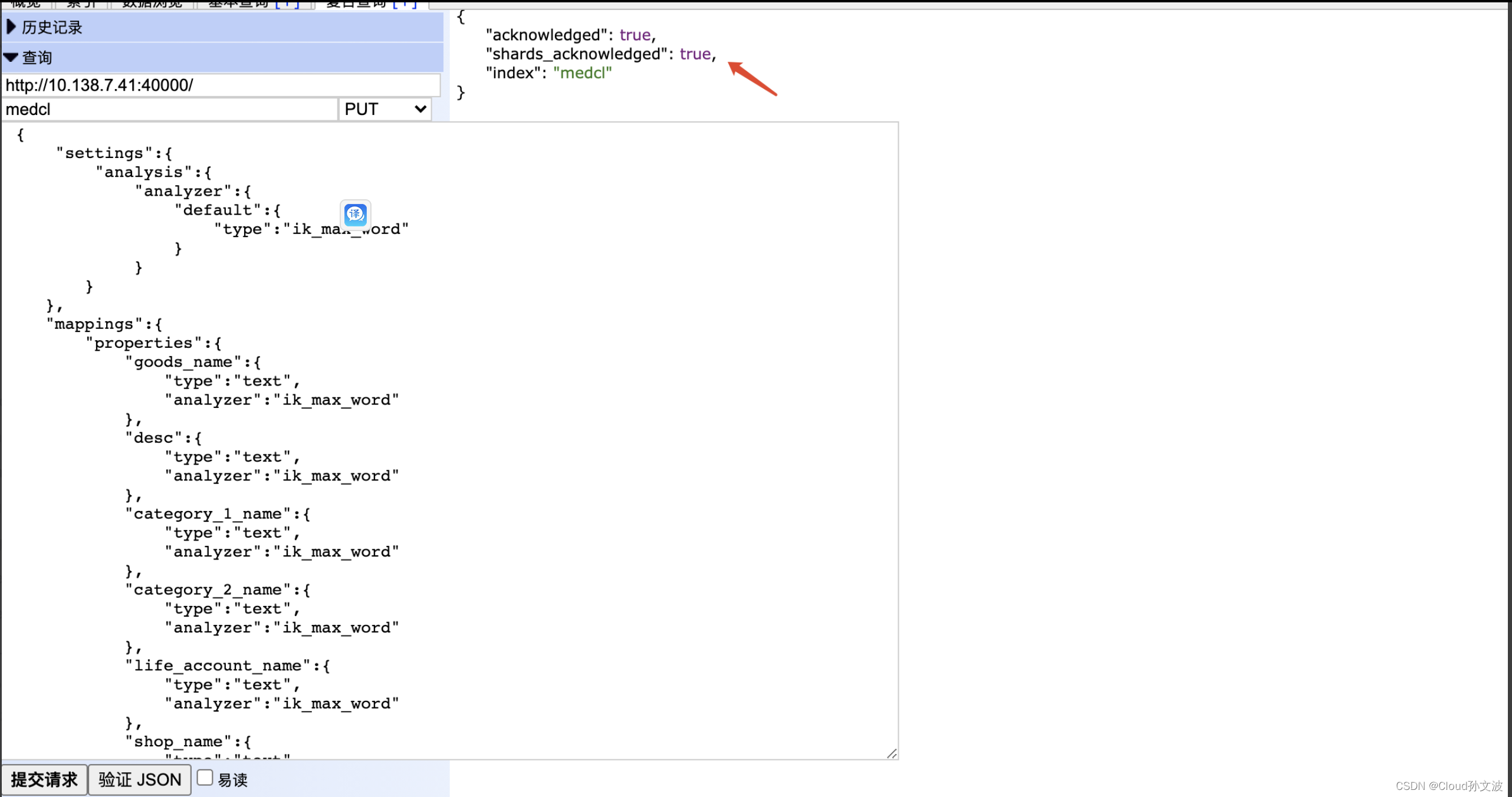
ElasticSearch 部署及安装ik分词器
ansiable playbook链接: https://download.csdn.net/download/weixin_43798031/87719490 需要注意的点:公司es集群现以三个角色部署分别为 Gateway、Master、Data 简单的理解可以理解为在每台机器上部署了三个es,以端口和配置文件来区分这三…...
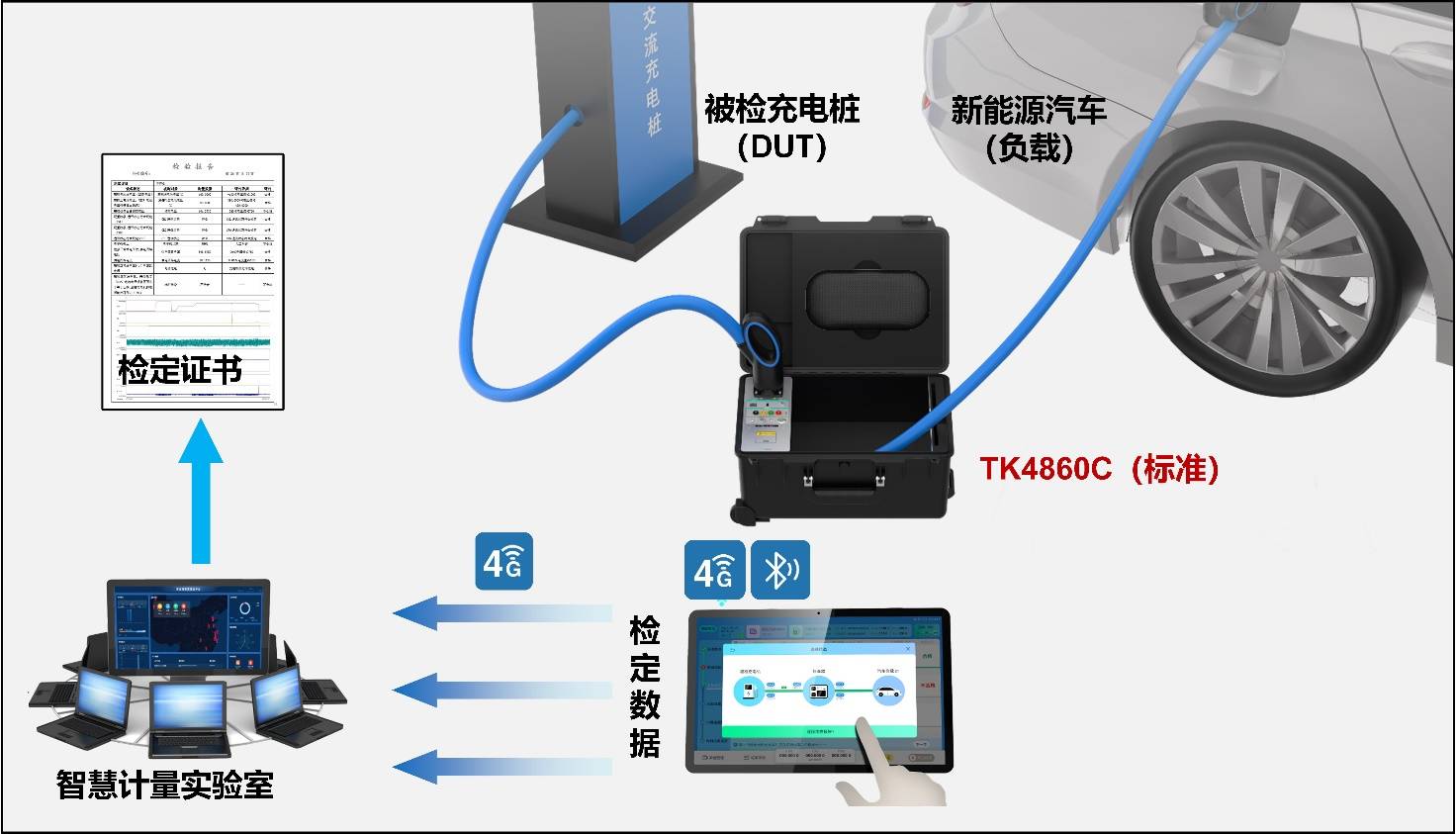
汽车充电桩检测设备TK4860C交流充电桩检定装置
TK4860C是一款在交流充电桩充电过程中实时检测充电电量的标准仪器,仪器以新能源车为负载,结合宽动态范围测量技术、电能ms级高速刷新等技术,TK4860C实现充电全过程的累积电能精准计量,相比于传统的预设检定点的稳态计量࿰…...

备份和恢复:确保数据安全
备份和恢复:确保数据安全 在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。 备份策略概述 在制定备份策略时&…...
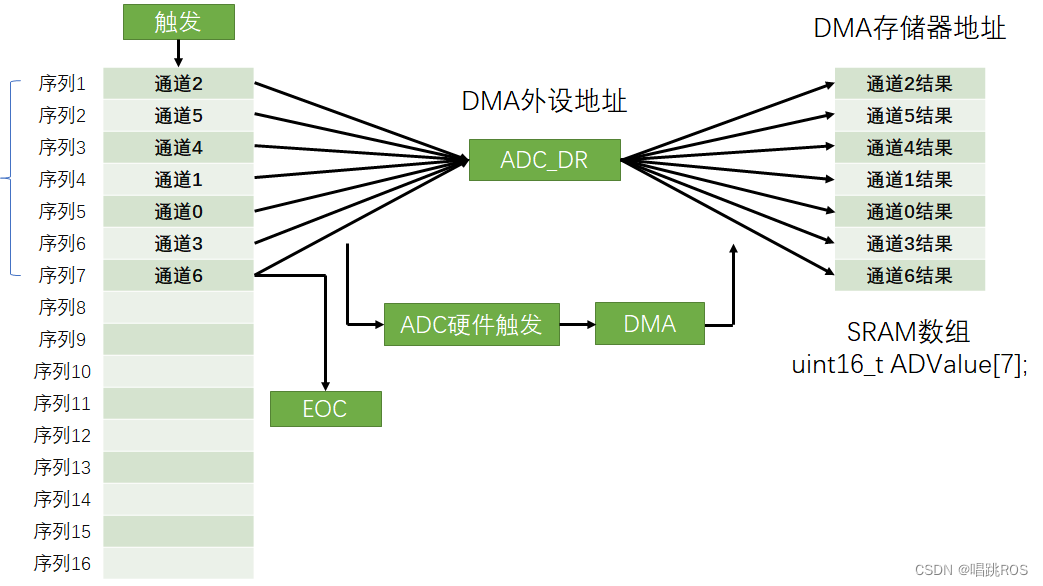
8 DWA(一)
8 DWA DMA简介 DMA(Direct Memory Access)直接存储器存取(可以直接访问32内部存储器,包括内存SRAM,Flash) DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&#x…...

mysql慢查询日志
概念 MySQL的慢查询日志是MySQL提供的一种日志记录,它用来记录在MySQL中响应时间超过阀值的语句,具体指运行时间超过long_query_time值的SQL,则会被记录到慢查询日志中。long_query_time的默认值为10,意思是运行10秒以上的语句。…...
Sentinel介绍及搭建
分布式流量防护 服务雪崩 服务提供者不可用导致服务调用者也跟着不可用,以此类推引起整个链路中的所有微服务都不可用 分布式流量防护 在分布式系统中,服务之间的相互调用会生成分布式流量。如何通过组件进行流量防护,并有效控制流量&…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
