哈希表题目:网格照明
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:网格照明
出处:1001. 网格照明
难度
6 级
题目描述
要求
在 n × n \texttt{n} \times \texttt{n} n×n 的二维网格 grid \texttt{grid} grid 上,每个单元格都有一盏灯,最初灯都处于关闭状态。
给你一个二维数组 lamps \texttt{lamps} lamps 表示灯的位置,其中 lamps[i] = [row i , col i ] \texttt{lamps[i] = [row}_\texttt{i}\texttt{, col}_\texttt{i}\texttt{]} lamps[i] = [rowi, coli] 表示打开位于 grid[row i ][col i ] \texttt{grid[row}_\texttt{i}\texttt{][col}_\texttt{i}\texttt{]} grid[rowi][coli] 的灯。即使同一盏灯在数组中出现多次,也是打开这盏灯。
当一盏灯打开时,会照亮自身单元格以及同一行、同一列和两条对角线上的所有其他单元格。
给你另一个二维数组 queries \texttt{queries} queries,其中 queries[j] = [row j , col j ] \texttt{queries[j] = [row}_\texttt{j}\texttt{, col}_\texttt{j}\texttt{]} queries[j] = [rowj, colj]。对于第 j \texttt{j} j 次查询,判断 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 是否被照亮。在回答第 j \texttt{j} j 次查询之后,关闭位于 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 的灯和相邻的 8 \texttt{8} 8 盏灯(如果存在)。如果一盏灯和 grid[row j ][col j ] \texttt{grid[row}_\texttt{j}\texttt{][col}_\texttt{j}\texttt{]} grid[rowj][colj] 共享边或角,则这盏灯是相邻的。
返回答案数组 ans \texttt{ans} ans,如果第 j \texttt{j} j 次查询的单元格被照亮,则 ans[j] \texttt{ans[j]} ans[j] 是 1 \texttt{1} 1,否则 ans[j] \texttt{ans[j]} ans[j] 是 0 \texttt{0} 0。
示例
示例 1:
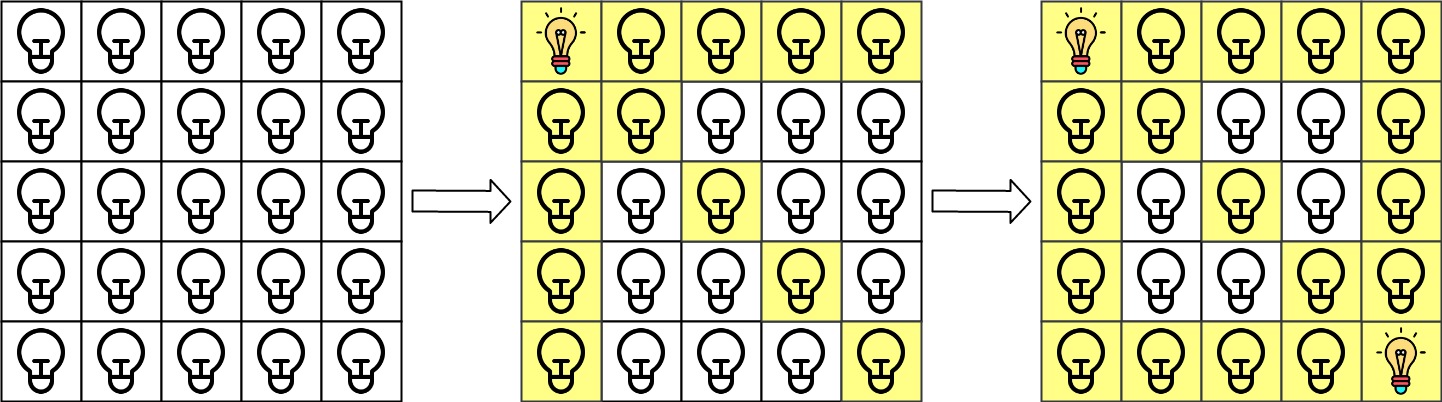
输入: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]] \texttt{n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]} n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出: [1,0] \texttt{[1,0]} [1,0]
解释:最初所有灯都是关闭的。上图中可以看到打开位于 grid[0][0] \texttt{grid[0][0]} grid[0][0] 的灯然后打开位于 grid[4][4] \texttt{grid[4][4]} grid[4][4] 的灯之后的网格。
第 0 \texttt{0} 0 次查询检查 grid[1][1] \texttt{grid[1][1]} grid[1][1] 是否被照亮(蓝色方框)。该单元格被照亮,所以 ans[0] = 1 \texttt{ans[0] = 1} ans[0] = 1。然后,关闭红色方框中的所有灯。
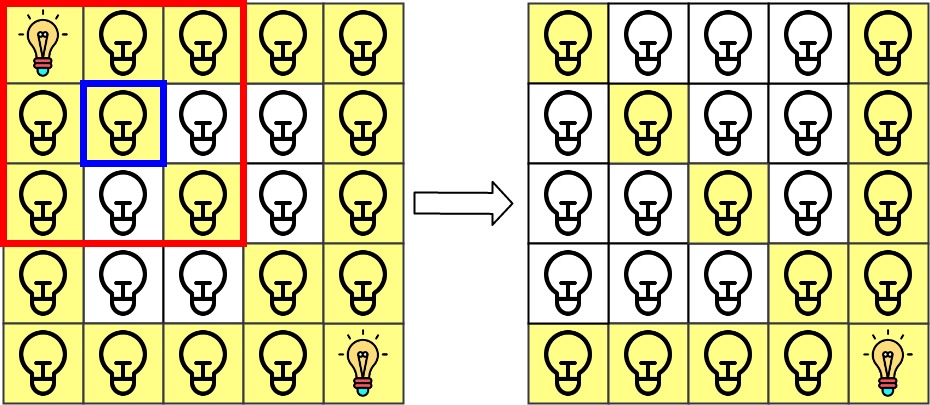
第 1 \texttt{1} 1 次查询检查 grid[1][0] \texttt{grid[1][0]} grid[1][0] 是否被照亮(蓝色方框)。该单元格没有被照亮,所以 ans[1] = 0 \texttt{ans[1] = 0} ans[1] = 0。然后,关闭红色矩形中的所有灯。
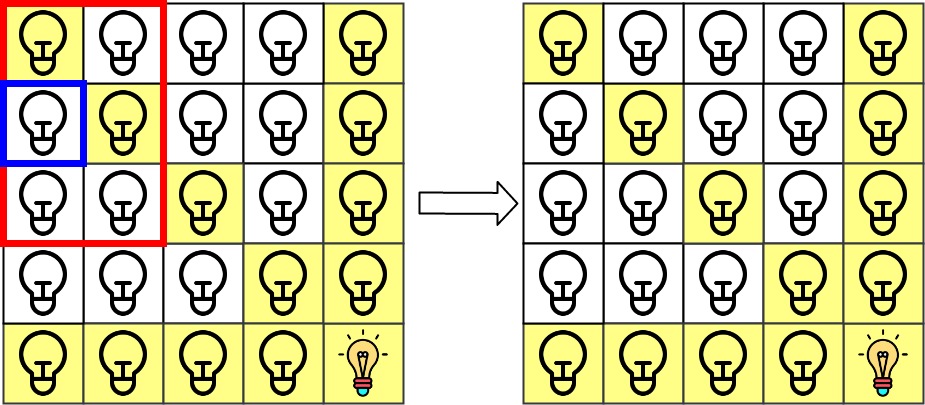
示例 2:
输入: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]] \texttt{n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]} n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出: [1,1] \texttt{[1,1]} [1,1]
示例 3:
输入: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]] \texttt{n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]} n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出: [1,1,0] \texttt{[1,1,0]} [1,1,0]
数据范围
- 1 ≤ n ≤ 10 9 \texttt{1} \le \texttt{n} \le \texttt{10}^\texttt{9} 1≤n≤109
- 0 ≤ lamps.length ≤ 20000 \texttt{0} \le \texttt{lamps.length} \le \texttt{20000} 0≤lamps.length≤20000
- 0 ≤ queries.length ≤ 20000 \texttt{0} \le \texttt{queries.length} \le \texttt{20000} 0≤queries.length≤20000
- lamps[i].length = 2 \texttt{lamps[i].length} = \texttt{2} lamps[i].length=2
- 0 ≤ row i , col i < n \texttt{0} \le \texttt{row}_\texttt{i}\texttt{, col}_\texttt{i} < \texttt{n} 0≤rowi, coli<n
- queries[i].length = 2 \texttt{queries[i].length} = \texttt{2} queries[i].length=2
- 0 ≤ row j , col j < n \texttt{0} \le \texttt{row}_\texttt{j}\texttt{, col}_\texttt{j} < \texttt{n} 0≤rowj, colj<n
解法
思路和算法
每个单元格都位于一行、一列和两条对角线上。一个单元格被照亮,等价于至少有一盏打开的灯和该单元格位于同一行、同一列或者同一条对角线上。因此,为了快速判断一个单元格是否被照亮,需要记录每一行、每一列和两个方向的每一条对角线上打开的灯的数量,可以使用哈希表记录。
维护四个哈希表,分别记录每一行打开的灯的数量、每一列打开的灯的数量、每一条方向一对角线上打开的灯的数量和每一条方向二对角线上打开的灯的数量,其中方向一对角线表示从左上到右下方向的对角线,方向二对角线表示从左下到右上方向的对角线。这四个哈希表分别称为行哈希表、列哈希表、对角线一哈希表和对角线二哈希表。
当 0 ≤ row , col < n 0 \le \textit{row}, \textit{col} < n 0≤row,col<n 时,如果位于第 row \textit{row} row 行第 col \textit{col} col 列的灯被打开,则需要将这盏灯存入四个哈希表。
-
由于灯所在的行是 row \textit{row} row,因此在行哈希表中将 row \textit{row} row 对应的数量加 1 1 1;
-
由于灯所在的列是 col \textit{col} col,因此在列哈希表中将 col \textit{col} col 对应的数量加 1 1 1;
-
由于在方向一对角线上,如果向左上移动一步则 row \textit{row} row 和 col \textit{col} col 同时减 1 1 1,如果向右下移动一步则 row \textit{row} row 和 col \textit{col} col 同时加 1 1 1,因此在同一条方向一对角线上的每个单元格满足 row − col \textit{row} - \textit{col} row−col 是定值,在对角线一哈希表中将 row − col \textit{row} - \textit{col} row−col 对应的数量加 1 1 1;
-
由于在方向二对角线上,如果向左下移动一步则 row \textit{row} row 加 1 1 1 且 col \textit{col} col 减 1 1 1,如果向右上移动一步则 row \textit{row} row 减 1 1 1 且 col \textit{col} col 加 1 1 1,因此在同一条方向二对角线上的每个单元格满足 row + col \textit{row} + \textit{col} row+col 是定值,在对角线二哈希表中将 row + col \textit{row} + \textit{col} row+col 对应的数量加 1 1 1。
数组 lamps \textit{lamps} lamps 表示打开的灯的位置。遍历数组 lamps \textit{lamps} lamps,对其中的每一个位置 [ row , col ] [\textit{row}, \textit{col}] [row,col],使用该位置更新四个哈希表。
由于数组 lamps \textit{lamps} lamps 中可能存在重复的位置,因此需要去重,避免同一个位置的灯被重复计算。去重的方法是使用哈希集合存储所有打开的灯的位置,哈希集合可以确保同一个位置只被加入一次。由于每一盏灯所在的行 row \textit{row} row 和列 col \textit{col} col 都是整数且都在范围 [ 0 , n − 1 ] [0, n - 1] [0,n−1] 内,因此可以定义哈希函数 f ( row , col ) = row × n + col f(\textit{row}, \textit{col}) = \textit{row} \times n + \textit{col} f(row,col)=row×n+col,该哈希函数可以确保不同位置对应的哈希值不同。
假设存在位置 [ row 1 , col 1 ] [\textit{row}_1, \textit{col}_1] [row1,col1] 和 [ row 2 , col 2 ] [\textit{row}_2, \textit{col}_2] [row2,col2] 满足 f ( row 1 , col 1 ) = f ( row 2 , col 2 ) f(\textit{row}_1, \textit{col}_1) = f(\textit{row}_2, \textit{col}_2) f(row1,col1)=f(row2,col2),则有 row 1 × n + col 1 = row 2 × n + col 2 \textit{row}_1 \times n + \textit{col}_1 = \textit{row}_2 \times n + \textit{col}_2 row1×n+col1=row2×n+col2,即 ( row 1 − row 2 ) × n = col 2 − col 1 (\textit{row}_1 - \textit{row}_2) \times n = \textit{col}_2 - \textit{col}_1 (row1−row2)×n=col2−col1。由于 ∣ row 1 − row 2 ∣ < n |\textit{row}_1 - \textit{row}_2| < n ∣row1−row2∣<n, ∣ col 2 − col 1 ∣ < n |\textit{col}_2 - \textit{col}_1| < n ∣col2−col1∣<n,且位置都是整数,因此一定有 row 1 − row 2 = col 2 − col 1 = 0 \textit{row}_1 - \textit{row}_2 = \textit{col}_2 - \textit{col}_1 = 0 row1−row2=col2−col1=0, [ row 1 , col 1 ] [\textit{row}_1, \textit{col}_1] [row1,col1] 和 [ row 2 , col 2 ] [\textit{row}_2, \textit{col}_2] [row2,col2] 是相同的位置。
定义哈希函数之后,根据哈希函数计算数组 lamps \textit{lamps} lamps 中的每个位置对应的哈希值。对于每个位置,只有当该位置的哈希值不在哈希集合中时,才将哈希值存入哈希集合,并使用该位置更新四个哈希表。
查询时,对于数组 queries \textit{queries} queries 中的每个位置 [ row , col ] [\textit{row}, \textit{col}] [row,col],首先判断该位置在四个哈希表中对应的数量是否大于 0 0 0,得到查询结果,然后将该位置和全部相邻位置的灯都关闭。具体做法如下。
-
在行哈希表中得到 row \textit{row} row 的数量、在列哈希表中得到 col \textit{col} col 的数量、在对角线一哈希表中得到 row − col \textit{row} - \textit{col} row−col 的数量、在对角线二哈希表中得到 row + col \textit{row} + \textit{col} row+col 的数量,如果该位置在四条线上对应的数量至少有一个大于 0 0 0 则查询结果是 1 1 1,如果该位置在四条线上对应的数量都是 0 0 0 则查询结果是 0 0 0。
-
遍历位置 [ row , col ] [\textit{row}, \textit{col}] [row,col] 和全部相邻位置,对于每个位置,如果该位置对应的哈希值在哈希集合中,则说明该位置的灯处于打开状态,需要关闭,将该位置对应的哈希值从哈希集合中删除,并将该位置在四个哈希表中对应的数量分别减 1 1 1。
查询时的关灯操作可以优化。如果一个单元格所在位置和全部相邻位置中至少有一盏灯打开,则该单元格一定被照亮,因此如果一个单元格没有被照亮,则该单元格所在位置和全部相邻位置的灯一定都处于关闭状态。只有当查询结果是 1 1 1 时,才需要执行关灯操作。
代码
class Solution {public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {Set<Long> set = new HashSet<Long>();Map<Integer, Integer> rowMap = new HashMap<Integer, Integer>();Map<Integer, Integer> columnMap = new HashMap<Integer, Integer>();Map<Integer, Integer> diagonal1Map = new HashMap<Integer, Integer>();Map<Integer, Integer> diagonal2Map = new HashMap<Integer, Integer>();for (int[] lamp : lamps) {int row = lamp[0], column = lamp[1];long position = (long) row * n + column;if (set.add(position)) {rowMap.put(row, rowMap.getOrDefault(row, 0) + 1);columnMap.put(column, columnMap.getOrDefault(column, 0) + 1);int diagonal1 = row - column;diagonal1Map.put(diagonal1, diagonal1Map.getOrDefault(diagonal1, 0) + 1);int diagonal2 = row + column;diagonal2Map.put(diagonal2, diagonal2Map.getOrDefault(diagonal2, 0) + 1);}}int[][] directions = {{0, 0}, {-1, -1}, {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}};int queriesCount = queries.length;int[] ans = new int[queriesCount];for (int j = 0; j < queriesCount; j++) {int[] query = queries[j];int queryRow = query[0], queryColumn = query[1];boolean flag = rowMap.containsKey(queryRow) || columnMap.containsKey(queryColumn) || diagonal1Map.containsKey(queryRow - queryColumn) || diagonal2Map.containsKey(queryRow + queryColumn);if (flag) {ans[j] = 1;for (int[] direction : directions) {int row = queryRow + direction[0], column = queryColumn + direction[1];int diagonal1 = row - column, diagonal2 = row + column;if (row >= 0 && row < n && column >= 0 && column < n) {long position = (long) row * n + column;if (set.remove(position)) {rowMap.put(row, rowMap.get(row) - 1);if (rowMap.get(row) == 0) {rowMap.remove(row);}columnMap.put(column, columnMap.get(column) - 1);if (columnMap.get(column) == 0) {columnMap.remove(column);}diagonal1Map.put(diagonal1, diagonal1Map.get(diagonal1) - 1);if (diagonal1Map.get(diagonal1) == 0) {diagonal1Map.remove(diagonal1);}diagonal2Map.put(diagonal2, diagonal2Map.get(diagonal2) - 1);if (diagonal2Map.get(diagonal2) == 0) {diagonal2Map.remove(diagonal2);}}}}}}return ans;}
}
复杂度分析
-
时间复杂度: O ( l + q ) O(l + q) O(l+q),其中 l l l 是数组 lamps \textit{lamps} lamps 的长度, q q q 是数组 queries \textit{queries} queries 的长度。需要遍历数组 lamps \textit{lamps} lamps,对于每个打开的灯的位置,将该位置存入哈希集合以及更新四个哈希表的时间都是 O ( 1 ) O(1) O(1),然后需要遍历数组 queries \textit{queries} queries,对于每个查询,计算查询结果以及更新哈希表和哈希集合的时间都是 O ( 1 ) O(1) O(1),因此总时间复杂度是 O ( l + q ) O(l + q) O(l+q)。
-
空间复杂度: O ( l ) O(l) O(l),其中 l l l 是数组 lamps \textit{lamps} lamps 的长度。需要使用四个哈希表记录打开的灯的数量以及使用哈希集合存储打开的灯的位置,哈希表和哈希集合的空间复杂度都是 O ( l ) O(l) O(l)。注意返回值不计入空间复杂度。
相关文章:

哈希表题目:网格照明
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:网格照明 出处:1001. 网格照明 难度 6 级 题目描述 要求 在 n n \texttt{n} \times \texttt{n} nn 的二维网格 grid \texttt{grid}…...

Python多线程爬虫为何效率低下?解析原因并提高爬虫速度的方法
目录 一、知识点二、多线程语法GIL单线程多线程单线程多线程 最后的惊喜 一、知识点 线程(Thread)也叫轻量级进程,是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。线程自己不拥有…...
)
Python 标准方形信号定义(完美实现)
之前我们介绍了如何定义一个标准的正弦信号,这里我们做一下延申,简单说明一下如何定义一个方形函数。 方形信号表达式 square signal = g ( t ) = sign [ sin ( 2 π f t +...
)
[Daimayuan] 走不出的迷宫(C++,图论,DP)
有一个 H H H 行 W W W 列的迷宫(行号从上到下是 1 − H 1−H 1−H,列号从左到右是 1 − W 1−W 1−W),现在有一个由 . 和 # 组成的 H 行 W 列的矩阵表示这个迷宫的构造,. 代表可以通过的空地,# 代表不…...

【LeetCode: 1416. 恢复数组 | 暴力递归=>记忆化搜索=>动态规划 】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
centos7查看磁盘io
1.查看所使用到的命令为iostat,centos7没有自带iostat,需要安装一下 2.安装iostat命令 yum -y install sysstat 3.使用iostat命令 iostat %user:表示用户空间进程使用 CPU 时间的百分比 %nice:表示用户空间进程以降低优先级的…...
浅析低代码开发的典型应用构建场景v
在数字经济蓬勃发展的大势之下,企业软件开发人员供给不足、开发速度慢、开发成本高、数字化和智能化成效不明显等问题日益凸出,阻碍了企业的数字化转型。 而近年来,低代码的出现推动了经济社会的全面提效,也成为人才供求矛盾的润…...
3 连续模块(二)
3.5 零极点增益模块 在控制系统设计和分析中,常用的函数包括 传递函数(tf)、零极点(zpk)和状态空间(ss)函数 传递函数(tf):用于表示线性时不变系统的输入输出…...
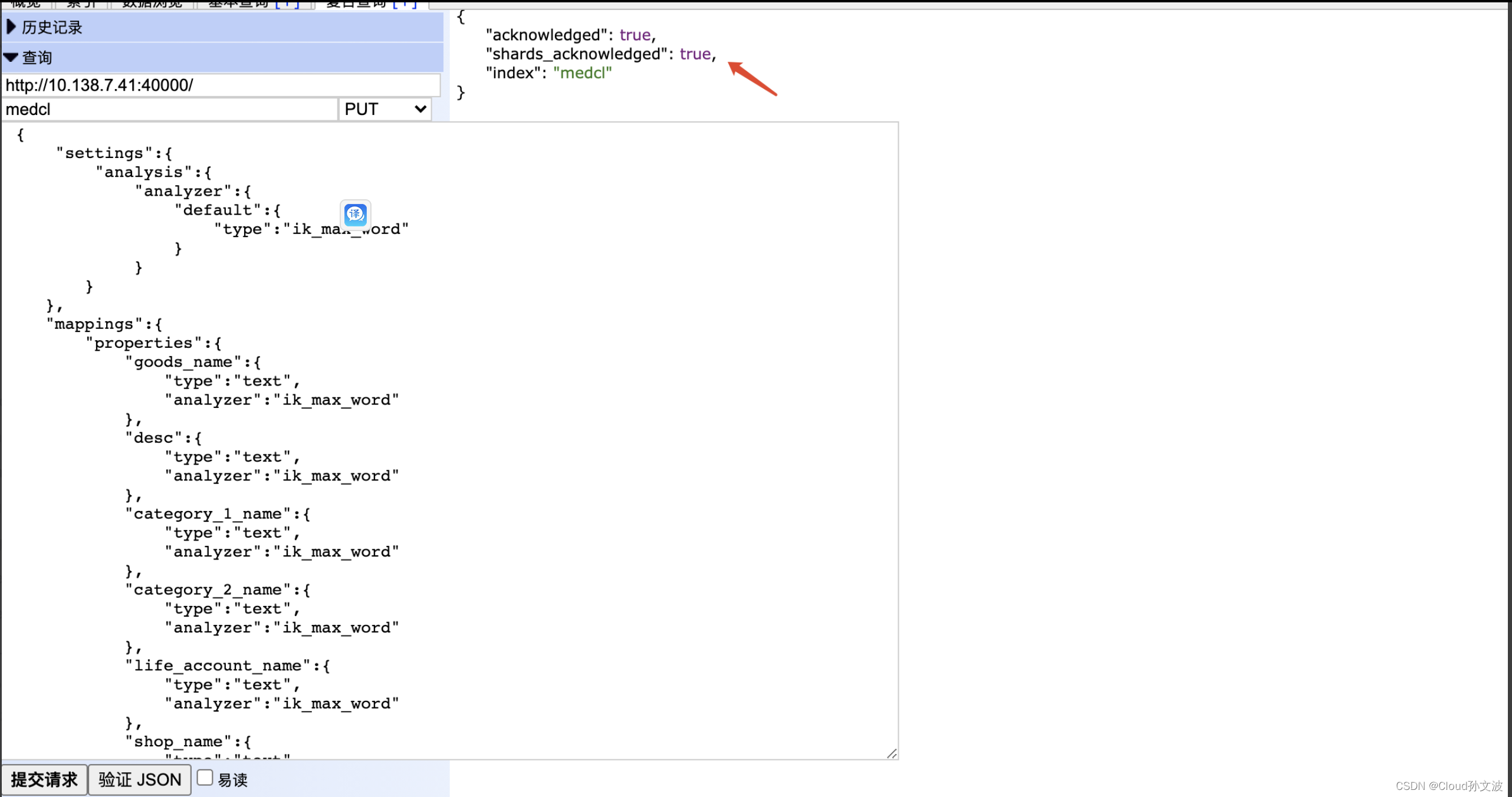
ElasticSearch 部署及安装ik分词器
ansiable playbook链接: https://download.csdn.net/download/weixin_43798031/87719490 需要注意的点:公司es集群现以三个角色部署分别为 Gateway、Master、Data 简单的理解可以理解为在每台机器上部署了三个es,以端口和配置文件来区分这三…...
汽车充电桩检测设备TK4860C交流充电桩检定装置
TK4860C是一款在交流充电桩充电过程中实时检测充电电量的标准仪器,仪器以新能源车为负载,结合宽动态范围测量技术、电能ms级高速刷新等技术,TK4860C实现充电全过程的累积电能精准计量,相比于传统的预设检定点的稳态计量࿰…...

备份和恢复:确保数据安全
备份和恢复:确保数据安全 在计算机领域中,备份和恢复数据对于确保数据安全至关重要。本文将介绍备份策略概述、使用mysqldump进行备份、使用MySQL Enterprise Backup进行备份、恢复数据以及备份和恢复的最佳实践。 备份策略概述 在制定备份策略时&…...
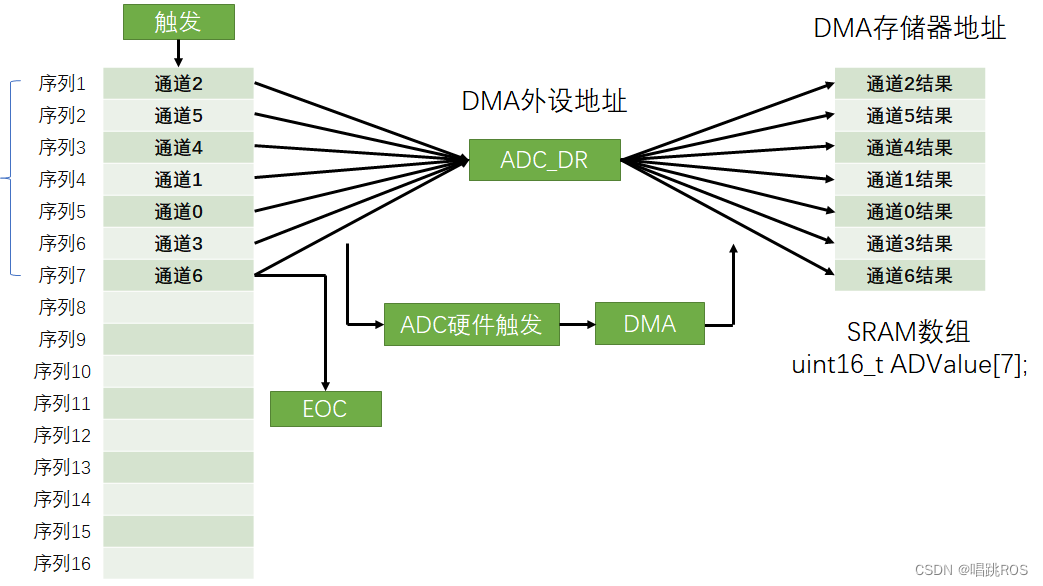
8 DWA(一)
8 DWA DMA简介 DMA(Direct Memory Access)直接存储器存取(可以直接访问32内部存储器,包括内存SRAM,Flash) DMA可以提供外设和存储器或者存储器和存储器之间的高速数据传输,无须CPU干预&#x…...

mysql慢查询日志
概念 MySQL的慢查询日志是MySQL提供的一种日志记录,它用来记录在MySQL中响应时间超过阀值的语句,具体指运行时间超过long_query_time值的SQL,则会被记录到慢查询日志中。long_query_time的默认值为10,意思是运行10秒以上的语句。…...
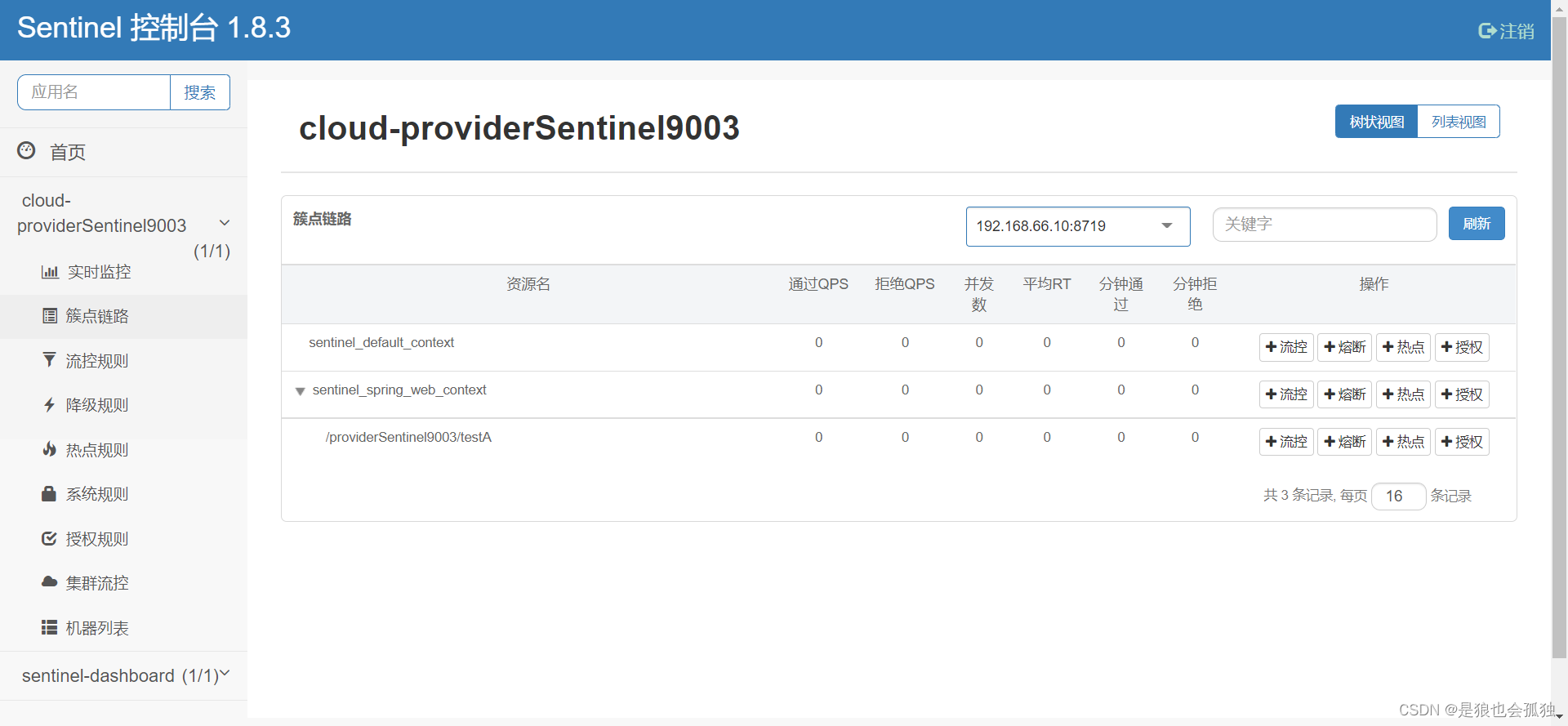
Sentinel介绍及搭建
分布式流量防护 服务雪崩 服务提供者不可用导致服务调用者也跟着不可用,以此类推引起整个链路中的所有微服务都不可用 分布式流量防护 在分布式系统中,服务之间的相互调用会生成分布式流量。如何通过组件进行流量防护,并有效控制流量&…...
最受信任的低代码平台排行榜
近年来,随着数字化转型的兴起,低代码平台获得了大量关注。它允许用户在几乎没有编码知识的情况下创建应用程序,从而使企业能够简化其流程并提高效率。随着低代码平台的日益流行,要确定哪些平台最可靠、最值得信赖并非易事。在本文…...
Django框架之创建项目、应用并配置数据库
django3.0框架创建项目、应用并配置数据库 创建项目 进入命令行 新建一个全英文的目录 进入目录 输入命令 django-admin startproject project 项目目录层级 查看当前目录层级 tree /f 目录文件说明 创建数据库 做一个学生管理系统做演示,使用navicat创建数据…...
软件测试之基础概念学习篇(需求 + 测试用例 + 开发模型 + 测试模型 + BUG)
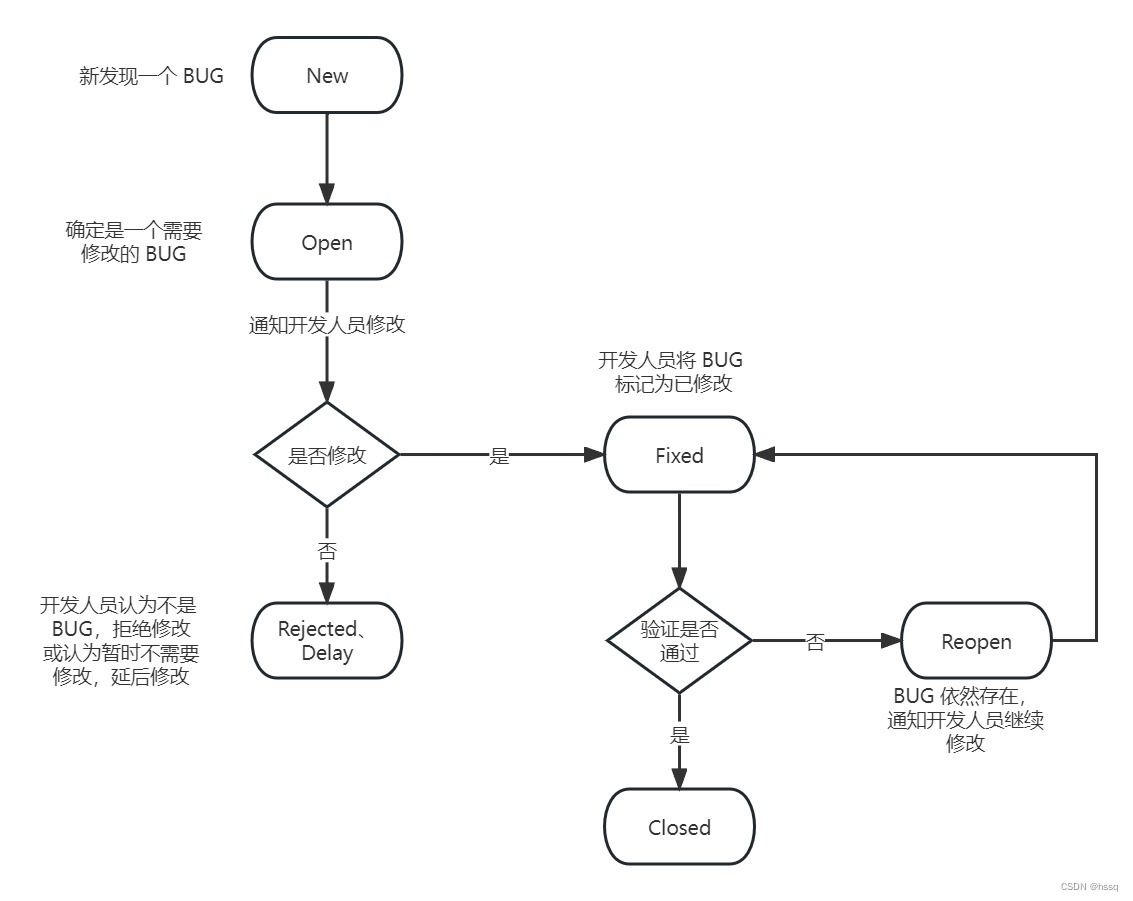
文章目录 1. 什么是软件测试2. 软件测试和软件开发的区别3. 软件测试和软件调试的区别4. 什么是需求1)以需求为依据设计测试用例 5. 测试用例是什么6. 什么是 BUG(软件错误)7. 五个开发模型1)瀑布模型2)螺旋模型3&…...
Windows下版本控制器(SVN) - 1、开发中的实际问题+2、版本控制简介
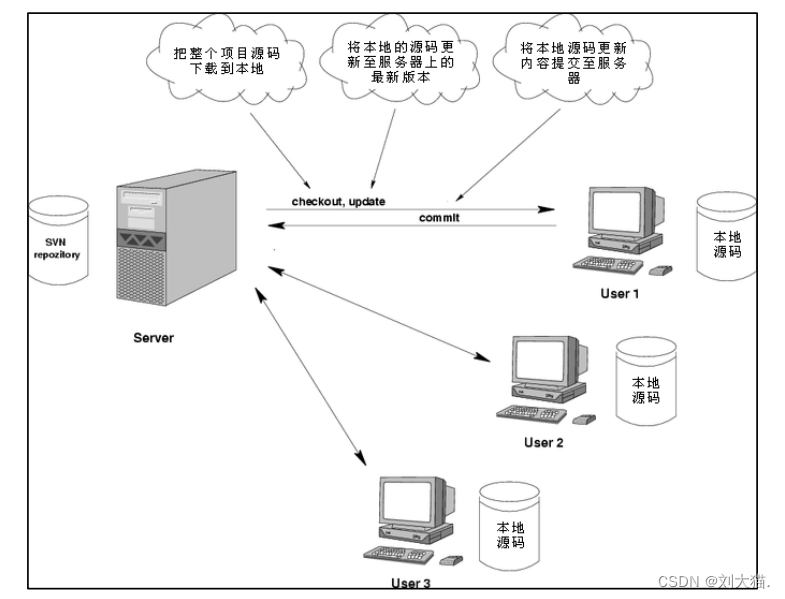
文章目录 基础知识-Windows下版本控制器(SVN)1、开发中的实际问题2、版本控制简介2.1 版本控制[Revision control]2.2 Subversion2.3 Subversion 的优良特性2.4 SVN 的工作原理:2.5 SVN 基本操作 本人其他相关文章链接 基础知识-Windows下版本控制器(SVN) 1、开发中…...

Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记
Learning Dynamic Facial Radiance Fields for Few-Shot Talking Head Synthesis 笔记 摘要 Talking head synthesis is an emerging technology with wide applications in film dubbing, virtual avatars and online education. Recent NeRF-based methods generate more n…...

SpringBoot 项目整合 Redis 教程详解
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
