【LeetCode】188. 买卖股票的最佳时机 IV
188. 买卖股票的最佳时机 IV(困难)



思路
状态定义
一、首先确定要一天会有几种状态,不难想到有四种:
- a.当天买入了股票;
- b.当天卖出了股票;
- c.当天没有操作,但是之前是买入股票的状态;
- d.当天没有操作,但是之前是卖出股票的状态;
同时操作四种状态有些复杂,通过分析,我们可以优化成两种状态:「当天持有股票」和「当天不持有股票」。这两种状态分别对应为 a/c 和 b/d 。
二、接下来考虑如何表示这两种状态:
- 最常见的方法是使用 dp[0] 和 dp[1] 来表示,但是这种方式不仅不方便识别数组,而且还增加了 dp数组的一个维度,就本题而言,这种定义方式会得到一个三维数组,难以操作。
- 所以建议直接使用能明确表示含义的两个dp数组,比如用 buy 表示持有股票的状态, sell 表示不持有股票的状态。
三、最后确定dp数组的维度:
- 首先必须要有表示天数 i 的维度;
- 还需要有表示买卖次数 k 的维度 j;
四、综上,得到了两个二维的dp数组:
buy[i][j]表示到第 i 天为止,恰好进行 j 笔交易,并且当前处于持有股票的状态,在这种情况下的最大利润;sell[i][j]表示到第 i 天为止,恰好进行 j 笔交易,并且当前处于不持有股票的状态,在这种情况下的最大利润;
确定递推公式
在确定递推公式的时候,需要明确一个概念: k什么时候发生变化。这道题默认一买一卖才算是一次完整的交易,所以只有在卖股票的情况下,k才会发生变化。
确定完k的变化后,递推公式就很容易得到,每种状态都由两种情况组合得到:
buy[i][j]- c.第 i-1 天就持有股票,那么当天收益不变,所得现金就是昨天持有股票的收益:
buy[i-1][j]; - a.第 i 天买入股票,所得现金就是昨天不持有股票的收益扣去今天的股票价格:
sell[i-1][j] - prices[i]; - 综合上述两种情况,最大收益就是
max(buy[i-1][j], sell[i-1][j] - prices[i])。
- c.第 i-1 天就持有股票,那么当天收益不变,所得现金就是昨天持有股票的收益:
sell[i][j]- d. 第 i-1 天就不持有股票,那么当天收益不变,所得现金就是昨天不持有股票的收益:
sell[i-1][j]; - b. 第 i 天售出股票,那么所得现金就是昨天持有股票的收益加上今天的股票价格:
buy[i-1][j-1] + prices[i]; - 综合上述两种情况,最大收益就是
max(sell[i-1][j], buy[i-1][j-1] + prices[i])。
- d. 第 i-1 天就不持有股票,那么当天收益不变,所得现金就是昨天不持有股票的收益:
根据我们对 k 的变化的定义,体现在递推公式中就是在推导 sell[i][j] 的第二种情况时用到的 buy[i-1][j-1] ,因为在卖出股票的时候,就完成了一次交易,因此k的次数加一,所以上一个持有股票的状态就是 j-1 。
dp数组的初始化
-
将所有的
buy[0][0...k]和sell[0][0...k]都设置为边界; -
对于
buy[0][0...k],由于对应 i = 0 ,因此只有 prices[0] 唯一的股价,所以如果要持有股票,只能选择买入,因此对于 k = 0,buy[0][0] = - prices[0]。由于只有一天,不可能完成一次完整的交易(即不可能售出),所以对于任意的 k >= 1 ,将所有的buy[0][1...k]设置一个非常小的值(这里使用 INT_MIN / 2) ,表示不合法的状态。 -
同理,对于
sell[0][0...k],对应于 i=0 ,只有 prices[0] ,所以如果要不持有股票,只能不进行任何操作,所以对于 k=0,sell[0][0] = 0,所以对于任意的 k >= 1 ,同样是不合法状态,将所有的buy[0][1...k]设置一个非常小的值(这里使用 INT_MIN / 2) 。
最终的返回结果
在遍历完所有的 prices 后,手上不持有股票对应的最大力利润一定严格大于手上持有股票对应的最大利润,然而完成的交易数不是越多越好(比如数组 prices 单调递减,此时不进行任何交易才是最优解),因此最终答案是 sell[n-1][0...k] 的最大值,即 return *max_element(sell[n-1].begin(), sell[n-1].end()); 。
易错点
一、k 的范围:
由于一次完整的交易需要两天,如果交易次数 k 大于 n/2 ,则必然有一天交易了两次,这是没有意义的,因此我们可以减小 k 的值,再进行动态规划,即 k = min(k, n/2); 。
二、buy 数组的维数:
第二个维度是 k+1 维,表示 k 的范围从 0~k 。如果数组单调递减,此时不进行任何交易是最优解, k=0;
三、j 的循环:
由于 sell[i][j] 的状态转移方程中包含 buy[i-1][j-1] ,如果 j=0 时,这是一个不合法状态,所以无需对 sell[i][j] 进行状态转移,让它保持值为 0 即可,所以在 j=0 时,只需要对 buy[i][0] 单独处理。
代码
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();if(n == 0) return 0;vector<vector<int>> buy(n, vector<int>(k+1));vector<vector<int>> sell(n, vector<int>(k+1));// k值的预处理k = min(k, n/2);// 预处理buy[0][0] = -prices[0];sell[0][0] = 0;for(int i=1; i<=k; ++i){// 不能设置为 INT_MINbuy[0][i] = sell[0][i] = INT_MIN / 2;}for(int i=1; i<n; ++i){buy[i][0] = max(buy[i-1][0], sell[i-1][0] - prices[i]);for(int j=1; j<=k; ++j){buy[i][j] = max(buy[i-1][j], sell[i-1][j] - prices[i]);sell[i][j] = max(sell[i-1][j], buy[i-1][j-1] + prices[i]);}}return *max_element(sell[n-1].begin(), sell[n-1].end());}
};
空间压缩
从上述代码不难发现,当前持有股票和当前不持有股票的最大收益都只和前一个状态有关,buy[i][j] = max(buy[i-1][j], sell[i-1][j] - prices[i]); sell[i][j] = max(sell[i-1][j], buy[i-1][j-1] + prices[i]); ,因此可以对两个数组进行空间压缩,只留下第二个维度。
代码如下:
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();if(n == 0) return 0;vector<int> buy(k+1);vector<int> sell(k+1);// k值的预处理k = min(k, n/2);// 预处理buy[0] = -prices[0];sell[0] = 0;for(int i=1; i<=k; ++i){// 不能设置为 INT_MINbuy[i] = sell[i] = INT_MIN / 2;}for(int i=1; i<n; ++i){buy[0] = max(buy[0], sell[0] - prices[i]);for(int j=1; j<=k; ++j){buy[j] = max(buy[j], sell[j] - prices[i]);sell[j] = max(sell[j], buy[j-1] + prices[i]);}}return *max_element(sell.begin(), sell.end());}
};
参考资料:188. 买卖股票的最佳时机 IV
相关文章:

【LeetCode】188. 买卖股票的最佳时机 IV
188. 买卖股票的最佳时机 IV(困难) 思路 状态定义 一、首先确定要一天会有几种状态,不难想到有四种: a.当天买入了股票;b.当天卖出了股票;c.当天没有操作,但是之前是买入股票的状态ÿ…...
android studio RadioButton单选按钮
1.定义 <!--单选按钮--> <TextViewandroid:layout_marginTop"10dp"android:layout_width"match_parent"android:layout_height"wrap_content"android:text"请选择你的性别:"> </TextView> <RadioGrou…...

AI大模型快速发展,我们该如何应对?
文章目录 提问问题范例Prompt 公式 如何准确提问 随着人工智能技术的不断发展,聊天型大语言模型工具如 ChatGPT 在解决各种实际问题时具有越来越广泛的应用。这一技术的快速发展,不仅带来了更高的工作效率和更高的精度,同时也改变了人类的工作…...
java多线程BlockingDeque的三种线程安全正确退出方法
本文介绍两种BlockingDeque在多线程任务处理时正确结束的方法 一般最开始简单的多线程处理任务过程 把总任务放入BlockingDeque创建多个线程,每个线程内逻辑时,判断BlockingDeque任务是否处理完,处理完退出,还有任务就BlockingDe…...

从STM32F407到AT32F407(一)
雅特力公司的MCU有着性能超群,价格优越的巨大优势,缺点是相关资料少一些,我们可以充分利用ST的现有资源来开发它。 我用雅特力的STM32F437开发板,使用原子 stm32f407的开发板自带程序,测试串口程序,原设定…...
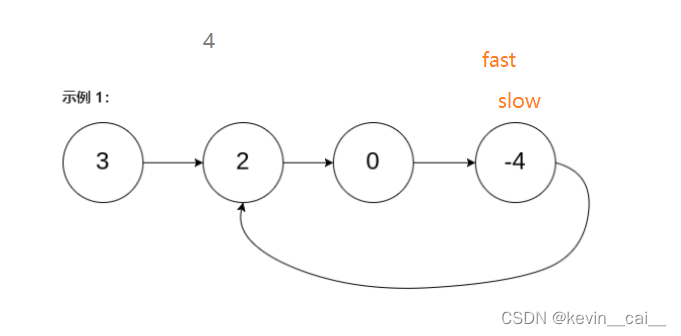
【数据结构】顺序表和链表基本实现(含全代码)
文章目录 一、什么是线性表1. 什么是顺序表动态开辟空间和数组的问题解释LeetCode-exercise 2. 什么是链表2.1链表的分类2.2常用的链表结构及区别2.3无头单向非循环链表的实现2.4带头双向循环链表的实现2.5循序表和链表的区别LeetCode-exercise 3. 快慢指针LeetCode-exercise 一…...
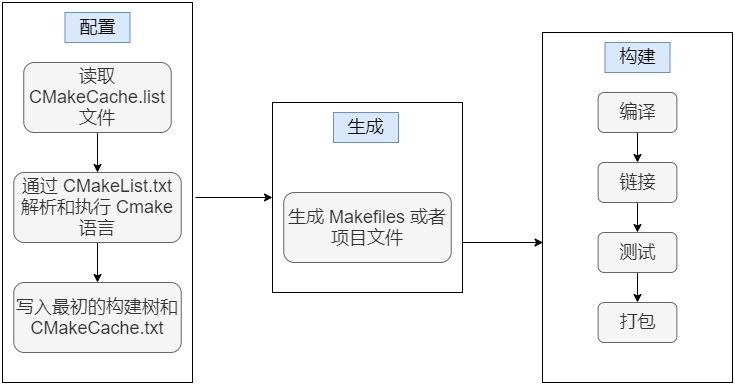
CMake : Linux 搭建开发 - g++、gdb
目录 1、环境搭建 1.1 编译器 GCC,调试器 GDB 1.2 CMake 2、G 编译 2.1 编译过程 编译预处理 *.i 编译 *.s 汇编 *.o 链接 bin 2.2 G 参数 -g -O[n] -l、-L -I -Wall、-w -o -D -fpic 3、GDB 调试器 3.1 调试命令参数 4、CMake 4.1 含义 4.2…...
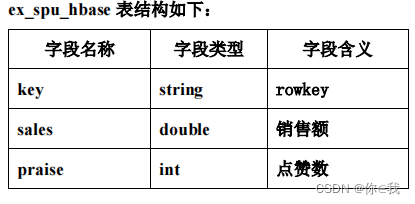
大数据实战 --- 美团外卖平台数据分析
目录 开发环境 数据描述 功能需求 数据准备 数据分析 RDD操作 Spark SQL操作 创建Hbase数据表 创建外部表 统计查询 开发环境 HadoopHiveSparkHBase 启动Hadoop:start-all.sh 启动zookeeper:zkServer.sh start 启动Hive: nohup …...

三大本土化战略支点,大陆集团扩大中国市场生态合作「朋友圈」
“在中国,大陆集团已经走过30余年的发展与耕耘历程,并在过去10年间投资了超过30亿欧元。中国市场也成为了我们重要的‘增长引擎’与‘定海神针’。未来,我们将继续深耕中国这个技术导向的市场。”4月19日上海车展上,大陆集团首席执…...

为什么停更ROS2机器人课程-2023-
机器人工匠阿杰肺腑之言: 我放弃了ROS2课程 真正的危机不是同行竞争,比如教育从业者相互竞争不会催生ChatGPT…… 技术变革的突破式发展通常是新势力带来的而非传统行业的升级改革。 2013年也就是10年前在当时主流视频网站开启分享: 比如 …...
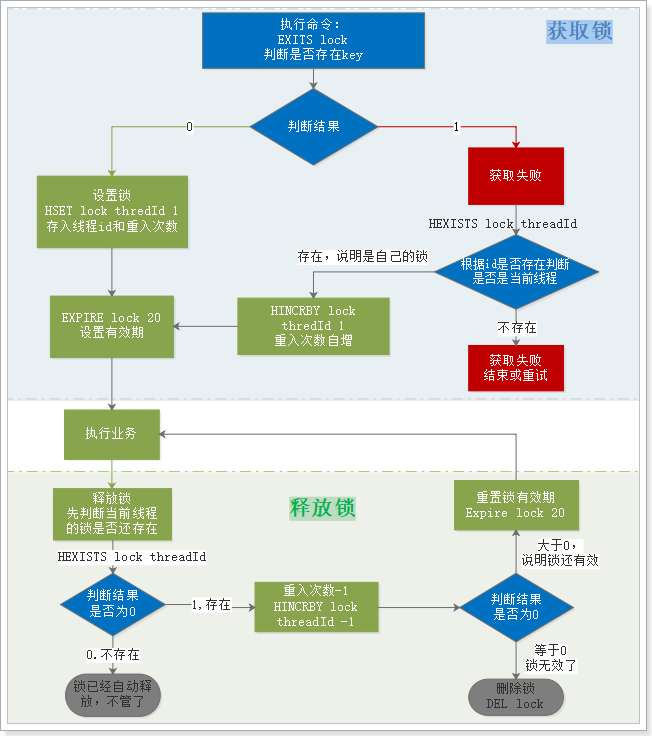
【SpringCloud常见面试题】
SpringCloud常见面试题 1.微服务篇1.1.SpringCloud常见组件有哪些?1.2.Nacos的服务注册表结构是怎样的?1.3.Nacos如何支撑阿里内部数十万服务注册压力?1.4.Nacos如何避免并发读写冲突问题?1.5.Nacos与Eureka的区别有哪些ÿ…...

ChatGPT+智能家居在AWE引热议 OpenCPU成家电产业智能化降本提速引擎
作为家电行业的风向标和全球三大消费电子展之一,4月27日-30日,以“智科技、创未来”为主题的AWE 2023在上海新国际博览中心举行,本届展会展现了科技、场景等创新成果,为我们揭示家电与消费电子的发展方向。今年展馆规模扩大至14个…...

拷贝构造函数和运算符重载
文章目录 拷贝构造函数特点分析拷贝构造函数情景 赋值运算符重载运算符重载operator<运算符重载 赋值运算符前置和后置重载 拷贝构造函数 在创建对象的时候,是不是存在一种函数,使得能创建一个于已经存在的对象一模一样的新对象,那么接下…...

本周热门chatGPT之AutoGPT-AgentGPT,可以实现完全自主实现任务,附部署使用教程
AutoGPT 是一个实验性的开源应用程序,它由GPT-4驱动,但有别于ChatGPT的是, 这与ChatGPT的底层语言模型一致。 AutoGPT 的定位是将LLM的"思想"串联起来,自主地实现你设定的任何目标。 简单的说,你只用提出…...

Mysql 优化LEFT JOIN语句
1.首先说一下个人对LEFT JOIN 语句的看法,原先我是没注意到LEFT JOIN 会影响到性能的,因为我平时在项目开发中,是比较经常见到很多个关联表的语句的。 2.阿里巴巴手册说过,连接表的语句最好不超过3次,但是我碰到的项目…...

全栈成长-python学习笔记之数据类型
python数据类型 数字类型 类型类型转换整型 intint() 字符串类型转换 浮点型保留整数 int(3.14)3 int(3.94)3浮点型 floatfloat() #####字符串类型 类型类型转换字符串 strstr() 将其他数据类型转为字符串 布尔类型与空类型 布尔类型 类型类型转换布尔型 boolbool()将其他…...

面试|兴盛优选数据分析岗
1.离职原因、离职时间点 2.上一份工作所在的部门、小组、小组人员数、小组内的分工 3.个人负责的目标,具体是哪方面的成本 4.为了降低专员成本,做了哪些方面的工作 偏向于机制、分析方法、思维,当下主要是对于部分高收入专员收入不合理的情况…...
主从复制master-slave replication)
Redis(08)主从复制master-slave replication
文章目录 redis主从复制一. 配置文件的方式设置1. 主节点配置:2. 从节点1配置:3. 从节点2配置: 二. 命令的方式设置1. 创建服务2. 设置主从节点3. 测试 三. 从节点升级为主节点四. 查看主从关系 redis主从复制 Redis主从复制是将一个Redis实例的数据复制到多个Redis实例&#…...
被chatGPT割了一块钱韭菜
大家好,才是真的好。 chatGPT热度一直上升,让我萌生了一个胆大而创新的想法, 把chatGPT嵌入到Notes客户机中来玩。 考虑到我已经下载了一个chatGPT的Notes应用(请见《ChatGPT APIs for HCL DOMINO》),想着…...
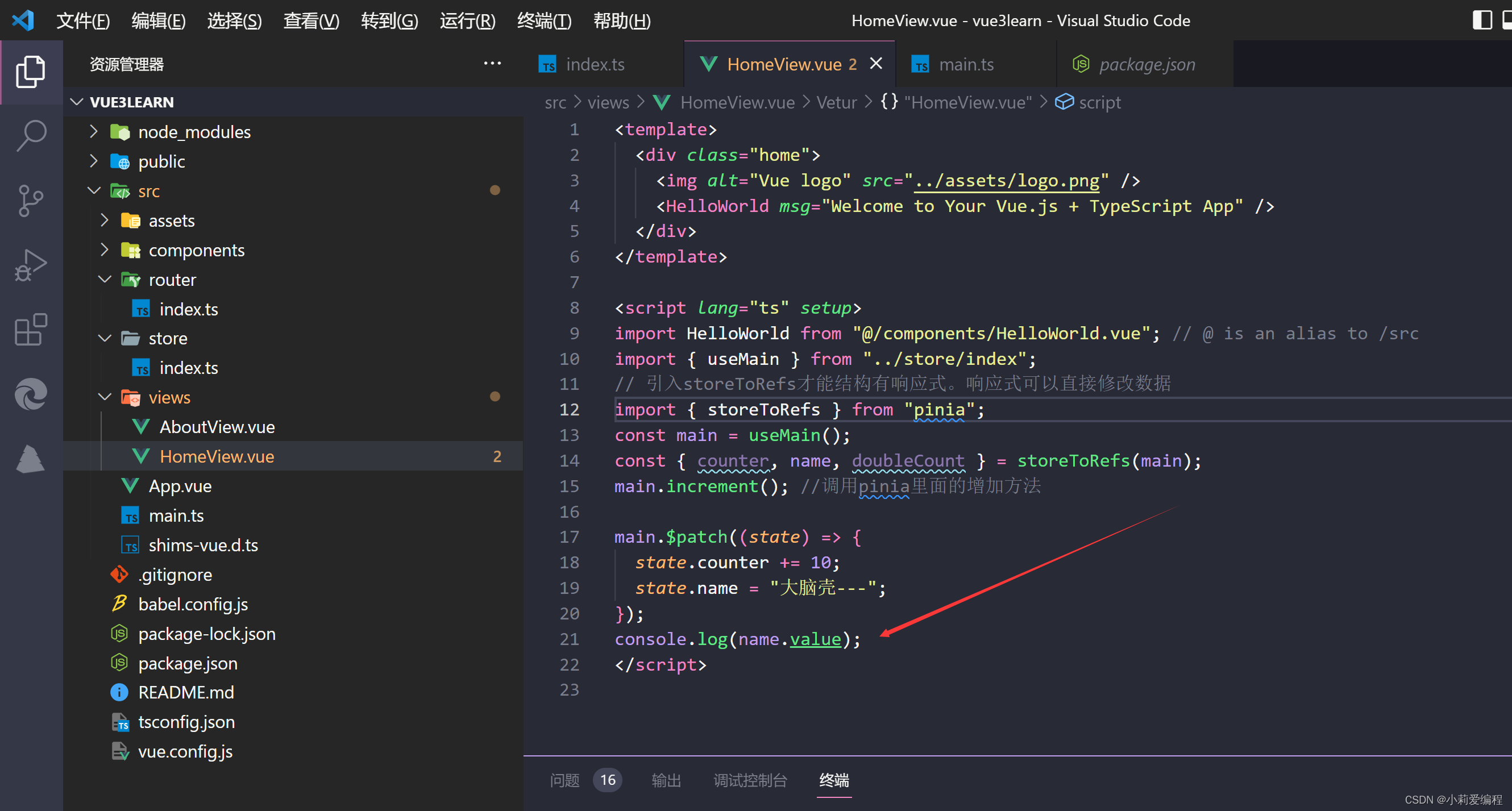
vue3+ts+pinia+vite一次性全搞懂
vue3tspiniavite项目 一:新建一个vue3ts的项目二:安装一些依赖三:pinia介绍、安装、使用介绍pinia页面使用pinia修改pinia中的值 四:typescript的使用类型初识枚举 一:新建一个vue3ts的项目 前提是所处vue环境为vue3&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
