MATLAB连续时间信号的实现和时域基本运算(八)
1、实验目的:
1)熟悉常用连续时间信号的实现方法;
2)掌握连续时间信号的时域基本运算;
3)掌握实现基本函数及其运算的函数的使用方法;
4)加深对信号基本运算的理解。
2、实验内容:
2-1)、利用数值法编程实现冲激信号δ(t-2)和阶跃信号u(t-1),并绘制两者的波形。(注:t取值范围[-1, 4])
t0 = -1; t1 = 0; t2 = 4; dt = 0.05; %dt是信号时间间隔
t = t0: dt: t2;
x = 1/dt*(t==2); %t=2时候的冲激函数
stairs(t,x);t0 = -1; t1 = 1; t2 = 4; dt = 0.05; %dt是信号时间间隔
t = t0:dt:t2;
k = length(t); %获取采样点的个数
n = floor((t1-t0)/dt); %求t1对应的样本序号
u = [zeros(1, n), ones(1, k-n)]
stairs(t, u);%绘制阶梯图
2-2)、分别利用数值法和符号法实现连续正弦信号f(t)=ksin(ωt+φ)的图形绘制,其中取k=2,ω=π,φ=π/3。(注:t取值范围[-2π, 2π])
% 数值法
clear
t = -2 : 0.01 : 2;
k = 2; w = pi; fai = pi/3;
ft = k*sin(w*t+fai);
plot(t,ft);% 符号法
clear
syms k w t fai;
k = 2; w = pi; fai = pi/3;
ft = k*sin(w*t+fai);
ezplot(ft,[-2,2]);
2-3)、利用数值法实现复指数信号
,并绘制其实部、虚部、模和相角图形(注:t取值范围[0, 3])。
t = -1 : 0.01 : 4; a = -3; b = 4;
ft = exp((a+j*b)*t);
subplot(2,2,1), plot(t,real(ft)), title('实部'), grid
subplot(2,2,3), plot(t,imag(ft)), title('虚部'), grid
subplot(2,2,2), plot(t,abs(ft)), title('模'), grid
subplot(2,2,4), plot(t,angle(ft)), title('相角'), grid
2-4)、利用数值法编程实现幅度为2,周期为1,占空比为0.5的周期性方波信号(注:t取值范围[-1, 2])。
t = -1 : 0.01 : 2;
y = 2*square(2*pi*t,50); %产方波信号,周期为1,占空比50%
stairs(t,y);
axis([-1,2,-2.2,2.2]);
2-5)、利用数值法实现两信号
的和与乘积运算,并绘制原始两信号与运算后的信号波形(注:t取值范围[0, 4])。
t = 0 : 0.01 : 4;
f1t = exp(-t);
f2t = sin(2*pi*t);
Sum = f1t+f2t;
p = f1t.*f2t; % 数组用点乘
plot(t, f1t, t, f2t); % 原函数f1t、f2t图像
hold on; % 保持图像
plot(t, Sum, t,p);% 和运算 乘积运算图像
hold off;
2-6)、利用数值法实现将信号y=sin(t)的频率增为原来的2倍,并将y取倒相后进行翻转,在三个窗口分别显示原图与其2倍频图形、2倍频与其倒相图形、2倍频倒相与其翻转图形(注:t取值范围[0, 4π],原图形用蓝实线(第一个图形),另一个用红虚线)。
t = 0 : 0.01 : 4*pi; y = sin(t); % 原信号
Double_Fre = sin(2*t); % 2倍频信号
subplot(1,3,1); plot(t, y, '-b', t, Double_Fre, '--r'); %蓝色实线, 红色虚线Double_Dao = -sin(2*t); % 2倍频的倒相信号
subplot(1,3,2); plot(t, Double_Fre, '-b', t, Double_Dao, '--r'); % 尺度变换Dou_Dao_fan = -sin(-2*t); %2倍频倒相其翻转图形
subplot(1,3,3); plot(t, Double_Dao, '-b', t, Dou_Dao_fan, '--r'); % 二倍频倒相与其翻转图像输出结果如下:
 我觉得没问题~_~
我觉得没问题~_~


% 利用sbus 函数改变变量clear
syms t;
ft = (1+t/2)*(heaviside(t+2)-heaviside(t-2)); %原函数ft
f1 = subs(ft, t, t-2); % f(t-2)
f2 = subs(ft, t, -t); % f(-t)
f3 = subs(ft, t, 2*t); % f(2t)
f4 = subs(ft, t, t/2+1); f4 = diff(f4); % 求导
f5 = subs(ft, t, 2-t); f5 = int(f5); % 积分subplot(2,3,1); ezplot(ft, [-3,3]); title('f');
subplot(2,3,2); ezplot(f1, [-1,5]); title('f1');
subplot(2,3,3); ezplot(f2, [-3,3]); title('f2');
subplot(2,3,4); ezplot(f3, [-3,3]); title('f3');
subplot(2,3,5); ezplot(f4, [-3,3]); title('f4');
subplot(2,3,6); ezplot(f5, [-3,6]); title('f5');


相关文章:

MATLAB连续时间信号的实现和时域基本运算(八)
1、实验目的: 1)熟悉常用连续时间信号的实现方法; 2)掌握连续时间信号的时域基本运算; 3)掌握实现基本函数及其运算的函数的使用方法; 4)加深对信号基本运算的理解。 2、实验内容&am…...

MongoDB 聚合管道中使用字符串表达式运算符
字符串表达式运算符主要用于实现字符串操作,主要包括了大小写转换、字符串截取、拼接、替换等 一、准备工作 初始化字符串数据 db.strings.insertMany([{ "_id": "1", "comment": " Abc" },{ "_id": "2&…...
用Python分析周杰伦歌曲并进行数据可视化
大家好,今天我们用python分析下周杰伦歌曲。为了尽量完整地呈现从原始数据到可视化的过程,接下来我们会先简单讲解数据的预处理过程,即如何将 JSON 数据转化为Excel 格式,以及如何对周杰伦的歌曲进行分词。 本案例中的歌词数据来…...

培训技能 GET
技巧 调整语速和语调:讲解者需要注意语速和语调的调整,以便让听众更好地理解和接受内容。 使用案例和实例:讲解者可以使用案例和实例来帮助听众更好地理解和记忆内容,同时也可以增强听众的兴趣和参与度。 互动式讲解:…...

数据库安全性案例分享
1 概述1.1 适用范围 本规范明确了Oracle数据库安全配置方面的基本要求。 1.2 符号和缩略语 缩写 英文描述 中文描述 DBA Database Administrator 数据库管理员 VPD Virtual Private Database 虚拟专用数据库 OLS Oracle Label Security Oracle标签…...
2023,你了解Kafka吗?深入详解
- 消息队列的核心价值 - 解耦合。 异步处理 例如电商平台,秒杀活动。一般流程会分为:1: 风险控制、2:库存锁定、3:生成订单、4:短信通知、5:更新数据。 通过消息系统将秒杀活动业务拆分开&#x…...

奇舞周刊第 491 期 初探 Web 客户端追踪技术
记得点击文章末尾的“ 阅读原文 ”查看哟~ 下面先一起看下本期周刊 摘要 吧~ 奇舞推荐 ■ ■ ■ 初探 Web 客户端追踪技术 浏览器的追踪技术是一把双刃剑,它建立了用户个人信息和网站之间的连接,合理地使用能够大大提高用户的体验,但是同时也…...
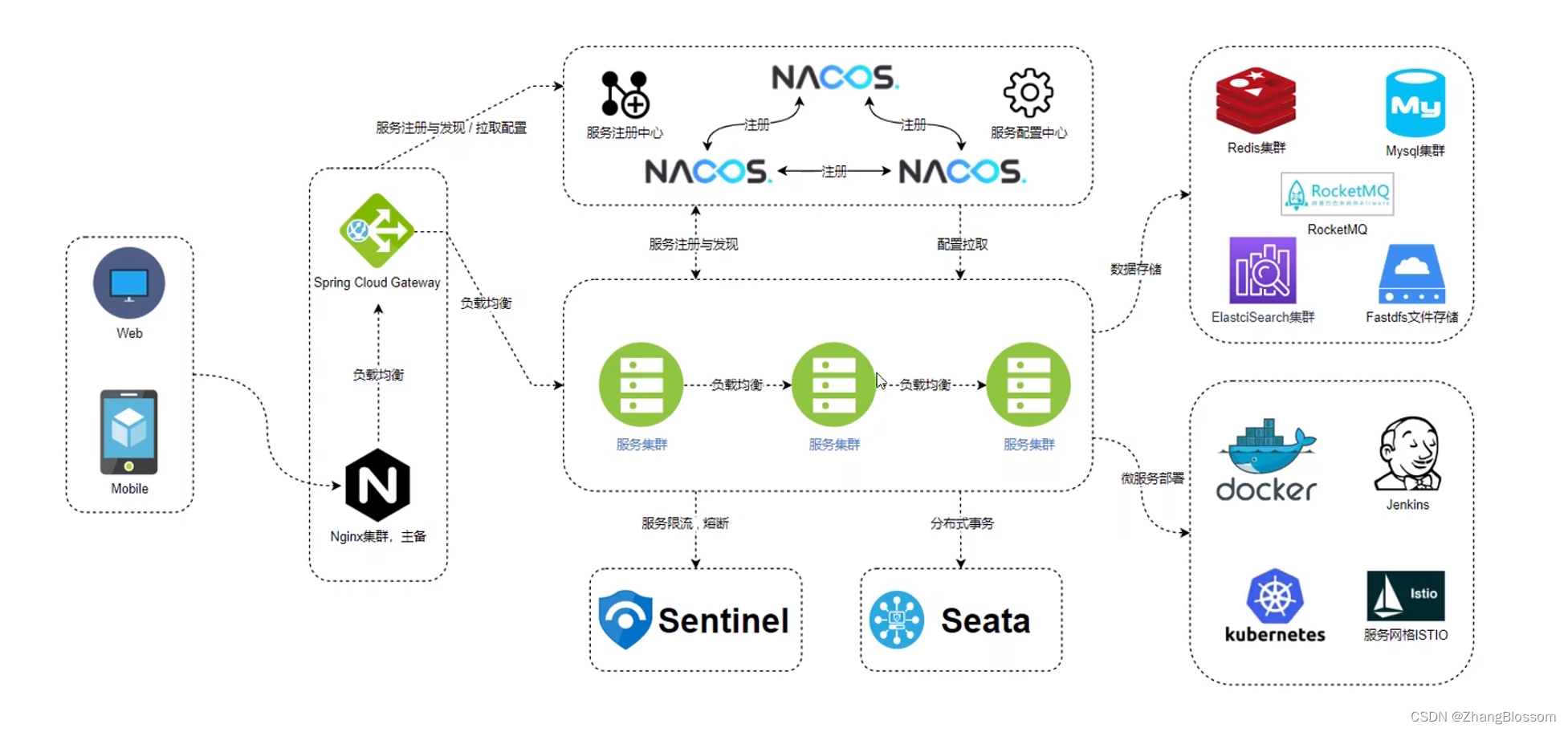
【Java】什么是SOA架构?与微服务有什么关系?
文章目录 服务化架构微服务架构 我的一个微服务项目,有兴趣可以一起做 服务化架构 我们知道,早期的项目,我们都是把前后端的代码放在同一个项目中,然后直接打包运行这个项目,这种项目我们称之为单体项目,比…...
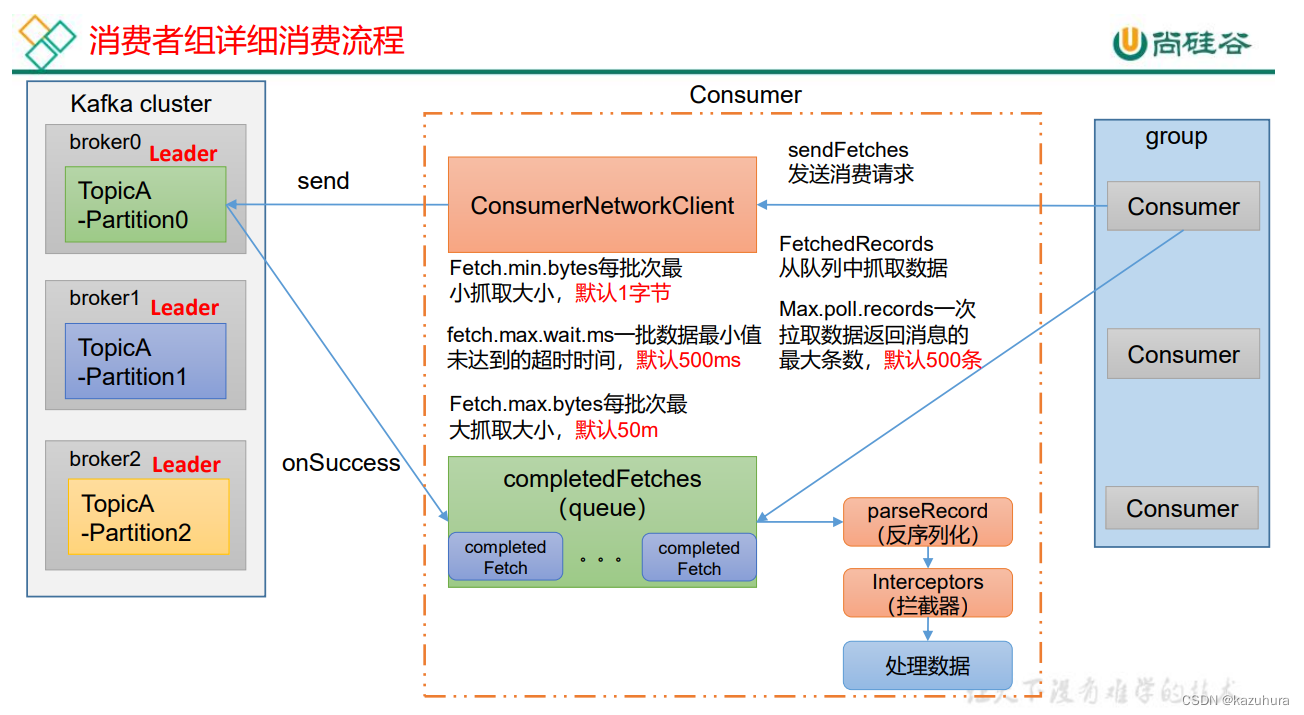
【中间件】kafka
目录 一、概述二、生产者1. 发送原理2. 生产者分区 Partition分区好处分区策略 3. 生产者如何提高吞吐量4. 数据可靠性ACK应答级别数据不丢失:ACK ISR数据不重复:幂等性数据有序 三、broker1. 工作流程2. 副本相关3. 底层存储4. 高效读写数据 四、消费者…...

Html5版音乐游戏制作及分享(H5音乐游戏)
这里实现了Html5版的音乐游戏的核心玩法。 游戏的制作借鉴了,很多经典的音乐游戏玩法,通过简单的代码将音乐的节奏与操作相结合。 可以通过手机进行游戏,准确点击下落时的目标,进行得分。 点击试玩 游戏内的下落数据是通过手打记…...
Python基于Pytorch Transformer实现对iris鸢尾花的分类预测,分别使用CPU和GPU训练
1、鸢尾花数据iris.csv iris数据集是机器学习中一个经典的数据集,由英国统计学家Ronald Fisher在1936年收集整理而成。该数据集包含了3种不同品种的鸢尾花(Iris Setosa,Iris Versicolour,Iris Virginica)各50个样本&am…...

【运动规划算法项目实战】如何实现简单的状态机
文章目录 简介一、状态机1.1 简介1.2 原理介绍1.3 使用方法二、行为树2.1 简介2.2 原理介绍2.3 使用方法三、如何实现一个简单的状态机四、其他的决策模型简介四、总结简介 在机器人算法中,状态机和行为树是常用的两种设计模式。它们能够帮助机器人在复杂的环境中更好地执行任…...

JavaScript实现用while语句计算1+n的和的代码
以下为用while语句计算1n的和实现结果的代码和运行截图 目录 前言 一、实现用while语句计算1n的和 1.1运行流程及思想 1.2代码段 1.3 JavaScript语句代码 1.4运行截图 【附加】用while计算110的和 1.1代码段 1.3 运行截图 前言 1.若有选择,您可以在目录里…...
Three.js教程:顶点索引复用顶点数据
推荐:将 NSDT场景编辑器 加入你3D工具链 其他工具系列: NSDT简石数字孪生 顶点索引复用顶点数据 通过几何体BufferGeometry的顶点索引属性BufferGeometry.index可以设置几何体顶点索引数据,如果你有WebGL基础很容易理解顶点索引的概念&#…...
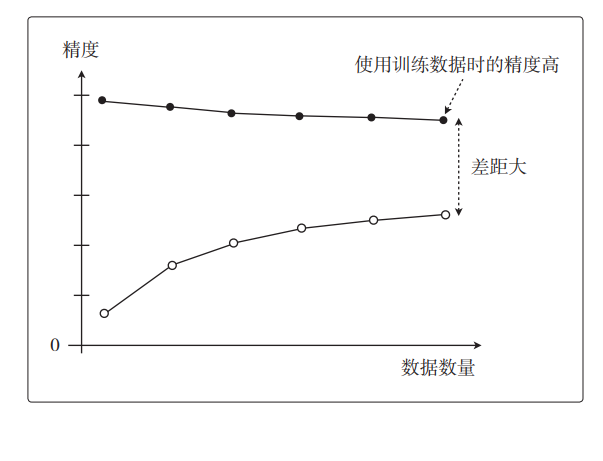
机器学习中的数学——学习曲线如何区别欠拟合与过拟合
通过这篇博客,你将清晰的明白什么是如何区别欠拟合与过拟合。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一下我在 机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言&…...
【Java】类和对象,封装
目录 1.类和对象的定义 2.关键字new 3.this引用 4.对象的构造及初始化 5.封装 //包的概念 //如何访问 6.static成员 7.代码块 8.对象的打印 1.类和对象的定义 对象:Java中一切皆对象。 类:一般情况下一个Java文件一个类,每一个类…...

Python小姿势 - 知识点:
知识点: Python的字符串格式化 标题: Python字符串格式化实例解析 顺便介绍一下我的另一篇专栏, 《100天精通Python - 快速入门到黑科技》专栏,是由 CSDN 内容合伙人丨全站排名 Top 4 的硬核博主 不吃西红柿 倾力打造。 基础知识…...

【Python】【进阶篇】9、Django路由系统精讲
目录 Django路由系统精讲1. Django 路由系统应用1)配置第一个URL实现页面访问2)正则与正则分组使用3)正则捕获组使用 2. path()与re_path() Django路由系统精讲 在《URL是什么》一节中,我们对 URL 有了基本的认识,在本…...
在Linux操作系统上部署wgcloud监控
1.wgcloud监控介绍 1.1 介绍 这是一款开源的主机监控系统,可以支持主机各种指标监测(cpu使用率,cpu温度,内存使用率,磁盘容量空间,磁盘IO,硬盘SMART健康状态,系统负载ÿ…...

浙大的SAMTrack,自动分割和跟踪视频中的任何内容
Meta发布的SAM之后,Meta的Segment Anything模型(可以分割任何对象)体验过感觉很棒,既然能够在图片上面使用,那肯定能够在视频中应用,毕竟视频就是一帧一帧的图片的组合。 果不其然浙江大学就发布了这个SAMTrack,就是在…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...
