代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ
代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ
完全背包
完全背包与01背包的区别在于每种物品都有无限件,可以多次放入背包。
我们回顾一下01背包的遍历顺序,其中内层遍历背包的过程要后序遍历,为什么当时一定要后序呢?
- 因为我们的递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);要求的当前节点数据用到的是前面的节点,我们后序遍历就能保证用到的前面节点是还没考虑放入当前物品i的情况。 - 如果我们使用正序遍历,那么前面的物品已经放入物品i了,那么就会导致再放一次物品i,也就违背了01背包的前提
由此,我们可以发现背包正序遍历可以实现多重背包问题,因为我们遍历容量是逐一递增的,所以每次递增最多也就多放一个物品i,不会出现说背包循环走一步可以放多个物品i,毕竟我们默认物品i重量是≥1的,<1的不考虑,应该也不会这么出题。
一些注意点:
-
一维dp数组实现的完全背包问题中,遍历背包和物品顺序可不可以调换?
- 可以
- 如果先遍历物品,后遍历背包。意味着每次遍历到下一个背包都去尝试是否能再放物品i,而不用管物品i在前一状态有没有被放过
- 如果先遍历背包,后遍历物品。意味着,一个个背包塞到最大价值再给下一个背包实现最大价值,后面的背包肯定会使用到前面背包的状态,这样也就会出现一些物品会被放多次的情况,并且每个背包都尽可能放入最大价值
-
现在我们回过头去思考此前01背包中,先遍历背包后遍历物品会怎么样?
这里我们肯定还是得保持背包后序遍历,这样的话一开始前面的背包都是清空状态,无法给最大的背包提供有效信息,它最终不一定能放最大价值,往后讨论也就没有意义了。
-
**注意注意:**先遍历物品得到的是组合;先遍历背包得到的是排列。在下面两题求解背包装满的方法数量有所体现。
代码:(01背包在遍历顺序上做了小调整)
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
518. 零钱兑换 II
题目介绍
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
个人思路:
本题很明显是背包问题,最大容量为amount,要我们求装满背包的最多方案,此外我们发现物品可以重复放入,故而这是一个完全背包问题。
动规五部曲
-
确定dp数组及其下标含义
int[] dp = new int[amount + 1]; //dp[j] 表示 容量为j的背包装满的方法 此题吧面额和重量看成一样 -
确定递推公式
dp[j] += dp[j - coins[i]];还是放与不放物品i的问题引入,装满容量为j的背包的方法 =已知方法数量 + 装满容量j拿出一个物品i的容量的背包的方法数量
-
初始化dp数组
dp[0] = 1;计算装满方法,统一操作了。 -
遍历顺序确定
-
虽然我们前面说完全背包求最大价值两次for循环可以调换顺序,但在这里不可以调换顺序,这里求的是组合方法,放满的方法数量。
-
先遍历物品,这种情况是组合情况
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3RYchxMU-1676306021084)(C:\Users\耿飞扬\AppData\Roaming\Typora\typora-user-images\image-20230214001843020.png)]
-
先遍历背包,这种情况会出现排列的情况,以遍历到背包3举例,
- 遍历物品1时,找到物品2,得到11 1、2 1两种情况
- 遍历物品2时,找到物品1,得到1 2一种情况
- 所以得到排列数情况
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xtPSDG7D-1676306021085)(C:\Users\耿飞扬\AppData\Roaming\Typora\typora-user-images\image-20230214002731595.png)]
-
背包要正序遍历
-
-
打印dp数组检验
代码
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount + 1];//dp[j] 表示 容量为j的背包装满的方法 此题吧面额和重量看成一样dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = 1; j <= amount; j++) {if (j - coins[i] >= 0)dp[j] += dp[j - coins[i]];}}return dp[amount];}
}
377. 组合总和 Ⅳ
题目介绍
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0
个人思路
原本这题是没写出来的,上一题可以说是碰巧过的吧,没有仔细思考排列组合受到循环内外层调换的影响。
上一题理清之后,本题就直接过了。思路也不过多阐述了,直接上代码,具体见上一题思路解析
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];//dp[j]:背包容量为j的背包装满的方法为dp[j]//初始化dp[0] = 1;for (int j = 1; j <= target; j++) {for (int i = 0; i < nums.length; i++) {if (j - nums[i] >= 0)dp[j] += dp[j - nums[i]];}}return dp[target];}
}
相关文章:

代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ
代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ 完全背包 完全背包与01背包的区别在于每种物品都有无限件,可以多次放入背包。 我们回顾一下01背包的遍历顺序,其中内层遍历背包的过程要后序遍历,为什么…...

【Bug】SQL无法绑定由多个部分组成的标识符
文章目录问题原因解决拓展问题 执行sql报:无法绑定由多个部分组成的标识符 原因 取了别名却没用别名,如下面这些情况 select * from biz_production_order_work_detail temp where biz_production_order_work_detail.create_time>2023-02-13selec…...

Games102 学习笔记
Games 102 P2 数据拟合 拟合数据的好坏 分段线性插值函数yf1(x)yf_1(x)yf1(x),数据误差为0,只有C0C_0C0连续。光滑插值函数yf2(x)yf_2(x)yf2(x),数据误差为0,可能被Noice带歪,导致函数性质不好,预…...

知识图谱基本知识点以及应用场景
近两年来,随着Linking Open Data等项目的全面展开,语义Web数据源的数量激增,大量RDF数据被发布。互联网正从仅包含网页和网页之间超链接的文档万维网(Document Web)转变成包含大量描述各种实体和实体之间丰富关系的数据万维网(Data Web)。在这…...

IDEA中常用的快捷键
IDEA中常用的快捷键 自动修正:ALT回车键 代码格式化:CTRLALTL 代码提示:CTRLALT空格 导入当前代码所需要的类:alt回车键 导入当前类中所需要的所有类:ctrlshifto 查看子类:ctrlh 查找类:ctrln …...

朗润国际期货招商:桥水基金四季度投资组合
桥水基金四季度投资组合 总持仓市值183.2亿美元;环比减少7.3% ishares标普500指数ETF:7.93亿占持仓4.33%环比1.14%宝洁:7.57亿占持仓4.13%环比-0.1%新兴市场core TEF-ishares:6.80亿占持仓3.71%环比0.47%强生:6.3亿占…...

Linux管道命令(pipe)全
目录 选取命令:cut、grep 传送门 排序命令:sort、wc、uniq 传送门 双向重定向:tee 字符转换命令:tr、col、join、paste、expand 传送门 划分命令:split 传送门 参数代换:xargs 传送门 关于减号…...

mybatis条件构造器(一)
mybatis条件构造器(一) 1 准备工作 1.1 建表sql语句(Emp表) SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0; -- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int NOT N…...

车联网之电子围栏中ConnectStreamed应用【二十】
文章目录 1. 电子围栏中ConnectStreamed应用1.1 ConnectedStreams简介1.1.1 connect流说明1.1.2 connect流使用场景1.2 Broadcast+Connect+CoFlatmap+CoMap整合实战1.3 两点之间球面距离计算1.4 电子围栏中自定义对象实现CoFlatMap函数1. 电子围栏中ConnectStreamed应用 1.1 C…...

临时文件tempfile
临时文件tempfile 1.概述 安全地创建具有唯一名称的临时文件,以至于他们不会被那些想破坏或者窃取数据的人猜出是非常有挑战性的。tempfile 模块提供了几个安全地创建系统临时文件的方法。 TemporaryFile() 打开并返回一个未命名的临时文件, NamedTemp…...

vue3封装数值动态递增组件
vue3封装数值动态递增组件前言源码举个例子:前言 1)使用技术: vue3.2 Ts 2)组件接收参数: 参数类型意义是否可选valuenumber数值大小必填durationnumber递增动画持续时间(单位:s)…...

JavaWeb_RequestResponse
目录 一、概述 二、Request对象 1.Request继承体系 2.Request获取请求数据 ①获取请求行数据 ②获取请求头数据 ③获取请求体数据 ④获取请求参数 3.Request请求转发 三、Response 1.Response设置响应数据功能 ①响应行 ②响应头 ③响应体 2.请求重定向 3.路径问…...

C语言刷题——“C”
各位CSDN的uu们你们好呀,今天,小雅兰要巩固一下之前学过的知识,那么,最好的复习方式就是刷题啦,现在,我们就进入C语言的世界吧 从最简单的开始噢 完完全全零基础都能看懂 题目来源于牛客网 编程语言初学训…...

【刷题】搜索——BFS:城堡问题(The Castle)
目录题目代码(Flood Fill)代码(并查集)题目 题目链接 找出房间个数——>求连通块个数 最大房间——>求最大连通块 直接用flood fill算法 注意题目的输入,例如118211182111821,则代表有西、北、南墙…...

深度学习——torch相关函数用法解析
1. torch.ones() torch.ones(*sizes, outNone) → Tensor函数功能:返回一个全为1 的张量,形状由可变参数sizes定义。 参数: sizes (int…) – 整数序列,定义了输出形状 out (Tensor, optional) – 结果张量 例子: >>> …...
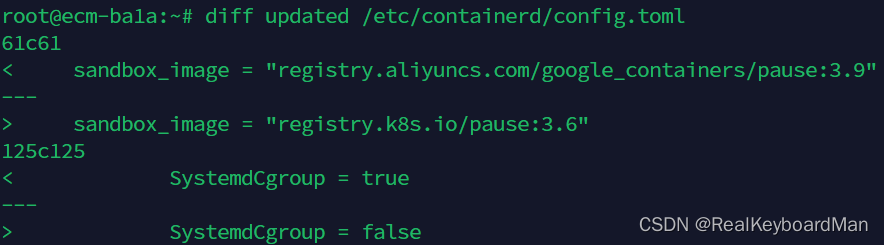
ubuntu 20使用kubeadm安装k8s 1.26
步骤 机器:4核8G,root账号,可访问互联网 1、更新apt apt-get update 2、安装一些基本工具 apt-get install ca-certificates curl gnupg lsb-release net-tools apt-transport-https 3、ifconfig 获取ip,hostname获取主机名&…...

低代码开发平台|制造管理-生产过程管理搭建指南
1、简介1.1、案例简介本文将介绍,如何搭建制造管理-生产过程。1.2、应用场景先填充工序信息,再设置工艺路线对应的工序;工序信息及工艺路线列表报表展示的是所有工序、工艺路线信息,可进行新增对应数据的操作。2、设置方法2.1、表…...
python对多个csv文件进行合并(表头需一致)
之前写过python对【多个Excel文件】中的【单个sheet】进行合并,参考:点我 之前也写过python对【多个Excel文件】中的【多个sheet】进行合并,参考:点我 今天再写一个python对多个csv格式的文件进行合并的小工具 但是大家切记&am…...

Salesforce Apex调用邮件模板
正常调用无模板:mail.setToAddresses(new List<String>{user.Email});//mail.setReplyTo(444298824qq.com);//mail.setCcAddresses(null);mail.setSenderDisplayName(EOP系统);mail.setSubject(EOP通知(待审批):您有未处理的…...
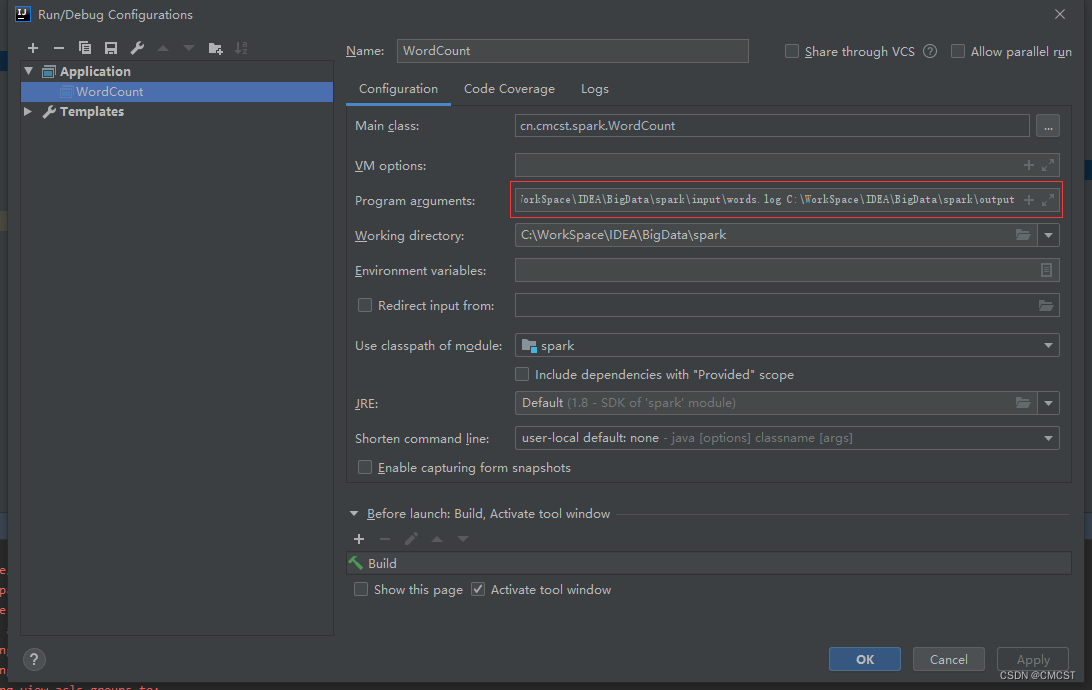
windows本地开发Spark[不开虚拟机]
1. windows本地安装hadoop hadoop 官网下载 hadoop2.9.1版本 1.1 解压缩至C:\XX\XX\hadoop-2.9.1 1.2 下载动态链接库和工具库 1.3 将文件winutils.exe放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.4 将文件hadoop.dll放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.5 将文件hadoop.dl…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
