*2.5 迭代法的收敛阶与加速收敛方法
学习目标:
-
了解迭代法的基本概念和原理。学习者需要理解迭代法的基本概念和原理,包括迭代过程、迭代格式、收敛性等基本概念。
-
熟练掌握迭代法的收敛阶和收敛速度。学习者需要了解迭代法的收敛阶和收敛速度,掌握如何计算迭代法的收敛阶和收敛速度,以及如何通过数值实验验证迭代法的收敛阶和收敛速度。
-
掌握迭代法的加速收敛方法。学习者需要了解迭代法的加速收敛方法,包括加速收敛的思想和方法,以及如何将加速收敛方法应用于具体的迭代法中。
-
熟练使用数值计算工具和编程语言进行迭代法的实现和应用。学习者需要熟练使用数值计算工具和编程语言,比如 MATLAB、Python 等,实现和应用迭代法及其加速收敛方法。
-
能够应用迭代法和加速收敛方法解决实际问题。学习者需要通过实际案例和应用,掌握如何应用迭代法和加速收敛方法解决实际问题,比如求解非线性方程、矩阵特征值问题等。
总之,学习者需要通过系统的学习和实践,掌握迭代法的收敛阶和加速收敛方法,并能够将其应用于实际问题的求解中。

收敛阶的定义:
在数值计算中,迭代法是一种重要的求解数值逼近问题的方法。在使用迭代法求解数值逼近问题时,我们通常需要关注迭代的收敛性能,而收敛阶就是评估迭代算法收敛性能的一种指标。
收敛阶是一个描述迭代算法收敛速度的概念。它是一个正整数或无穷大,通常用符号 p 表示。收敛阶的含义是:在每次迭代中,误差的大小至少缩小到前一次迭代误差的 p 倍。如果收敛阶 p 越大,则说明迭代算法的收敛速度越快。
具体来说,假设我们使用一个迭代算法求解一个方程的近似解 x。在第 k 次迭代后,我们得到的近似解为 x_k,真实解为 x。误差 e_k 可以定义为 e_k = x - x_k。那么,如果迭代算法的收敛阶为 p,则我们有以下关系式:
|e_{k+1}| <= C |e_k|^p
其中,C 是一个与迭代算法和问题本身相关的常数,|e_k| 表示误差的范数,比如 2-范数、无穷范数等。
简单来说,收敛阶 p 表示误差在每次迭代中至少缩小 p 倍。如果 p 越大,则说明迭代算法的收敛速度越快。在实际应用中,我们通常需要通过数值实验来估计迭代算法的收敛阶,并根据收敛阶的大小来评估迭代算法的性能和选择合适的算法和参数。

我的理解:
可以通过一个简单的例子来理解收敛阶的概念。
假设我们要求解方程 f(x) = 0 的近似解,其中 f(x) 是一个连续可微的函数。我们可以使用牛顿迭代法来求解,迭代格式为:
x_{k+1} = x_k - f(x_k) / f'(x_k)
其中,x_k 表示第 k 次迭代的近似解,f'(x_k) 表示 f(x) 在 x_k 处的导数。
我们假设迭代算法的收敛阶为 p。在第 k 次迭代后,误差 e_k 可以定义为 e_k = x - x_k,其中 x 是真实解。假设我们知道误差 e_{k+1} 和 e_k 的大小,我们可以通过以下关系式来估计迭代算法的收敛阶 p:
|e_{k+1}| <= C |e_k|^p
其中,C 是一个与迭代算法和问题本身相关的常数。
我们可以将上式取对数,得到:
log(|e_{k+1}|) <= p log(|e_k|) + log(C)
这个式子看起来和直线方程 y = mx + b 很相似,其中 p 就是斜率,log(C) 就是截距。
如果我们将误差的对数取代误差本身,我们会得到一条斜率为 p,截距为 log(C) 的直线。我们可以通过这条直线来判断迭代算法的收敛阶,即使我们并不知道真实解 x 的值。
比如,如果我们在图上画出误差的对数和迭代次数的关系图,如果看到一个斜率为 2 的直线,那么我们可以认为迭代算法的收敛阶为 2,即误差至少每次缩小到前一次的平方。如果看到一个斜率为 1 的直线,那么我们可以认为迭代算法的收敛阶为 1,即误差每次减少相同的倍数。如果看到一个斜率为 0 的直线,那么我们可以认为迭代算法不收敛,或者收敛的非常缓慢。
通过理解收敛阶的概念,我们可以更好地理解迭代算法的收敛性能,并且在实际应用中选择合适的算法和参数。

怎么用:
掌握收敛阶的概念可以帮助我们在实际应用中更好地选择和优化算法,并且提高算法的收敛速度和精度。以下是一些具体的应用场景:
-
选择最优的迭代算法:在实际应用中,可能有多种迭代算法可以求解同一个问题。掌握收敛阶的概念可以帮助我们评估不同算法的收敛速度和精度,从而选择最优的算法。
-
优化算法参数:在迭代算法中,通常有一些参数可以调整,例如步长、迭代次数等。掌握收敛阶的概念可以帮助我们理解这些参数对算法收敛速度和精度的影响,从而调整算法参数以获得更好的性能。
-
评估算法的收敛速度和精度:掌握收敛阶的概念可以帮助我们评估算法的收敛速度和精度,从而判断算法是否满足应用要求。
-
优化数值计算:在数值计算中,例如求解微分方程、积分等问题,通常需要使用迭代算法。掌握收敛阶的概念可以帮助我们选择和优化迭代算法,从而提高数值计算的精度和效率。
总之,掌握收敛阶的概念可以帮助我们更好地理解和应用迭代算法,提高算法的收敛速度和精度,从而在科学计算、优化算法等领域获得更好的应用效果。

前置知识:
拉格朗日微分中值定理(这个知识点看我高等数学的文章)传送门:3.1 微分中值定理
艾特基加速方法:
艾特肯算法(Aitken's delta-squared method),也称作Aitken加速算法,是一种加速迭代法的方法。
在使用迭代法求解某个问题时,如果每次迭代的值收敛得比较慢,我们可以通过加速迭代的方式来提高收敛速度。艾特肯算法就是一种常用的加速迭代的方法。
艾特肯算法的思想很简单,即通过利用连续三个近似解的差值,来得到一个更快收敛的新近似解。具体地,我们设迭代过程中的近似解为$x_n$,则用以下公式可以得到一个新的近似解:
$x_{n,acc} = x_n - \frac{(x_{n+1}-x_n)^2}{x_{n+1}-2x_n+x_{n-1}}$
其中,$x_{n+1}$表示第$n+1$次迭代得到的近似解,$x_{n-1}$表示第$n-1$次迭代得到的近似解。$x_{n,acc}$表示通过艾特肯算法得到的新的近似解。
艾特肯算法的优点是简单易实现,并且在某些情况下可以显著提高收敛速度。但是需要注意的是,在某些情况下,艾特肯算法可能会导致数值不稳定,因此需要谨慎使用。
总结:
收敛阶是用来描述迭代法的收敛速度的指标,一般越高表示收敛速度越快。它的重点在于理解概念和计算方法,其中需要注意的难点和易错点包括理解收敛阶和收敛速度的关系、理解如何通过计算近似解的误差来计算收敛阶、注意近似解的误差和真实解的误差之间的区别。
加速收敛方法是用来提高迭代法的收敛速度的一种方法。常见的加速收敛方法包括牛顿法、割线法、埃特金加速法等。它的重点在于了解不同加速收敛方法的思想、原理和应用场景,以及掌握它们的具体计算方法。需要注意的难点和易错点包括了解不同加速方法的数学原理、掌握迭代公式的计算和理解加速方法的数值稳定性。
艾特肯算法是一种常用的加速迭代法的方法,其思想是利用连续三个近似解的差值来得到一个更快收敛的新近似解。它的重点在于理解算法的思想和应用场景,以及掌握它的具体计算方法。需要注意的难点和易错点包括注意数值稳定性和理解算法中的分母接近于0时可能出现的波动。

相关文章:

*2.5 迭代法的收敛阶与加速收敛方法
学习目标: 了解迭代法的基本概念和原理。学习者需要理解迭代法的基本概念和原理,包括迭代过程、迭代格式、收敛性等基本概念。 熟练掌握迭代法的收敛阶和收敛速度。学习者需要了解迭代法的收敛阶和收敛速度,掌握如何计算迭代法的收敛阶和收敛…...

仪表板展示 | X-lab开放实验室GitHub开源项目洞察大屏
背景介绍 X-lab开放实验室是一个开源软件产业开放式创新的共同体,由来自国内外著名高校、创业公司、部分互联网与IT企业的专家学者与工程师所构成,目前已在包括开源治理标准制定、开源社区行为度量与分析、开源社区流程自动化、开源全域数据治理与洞察等…...
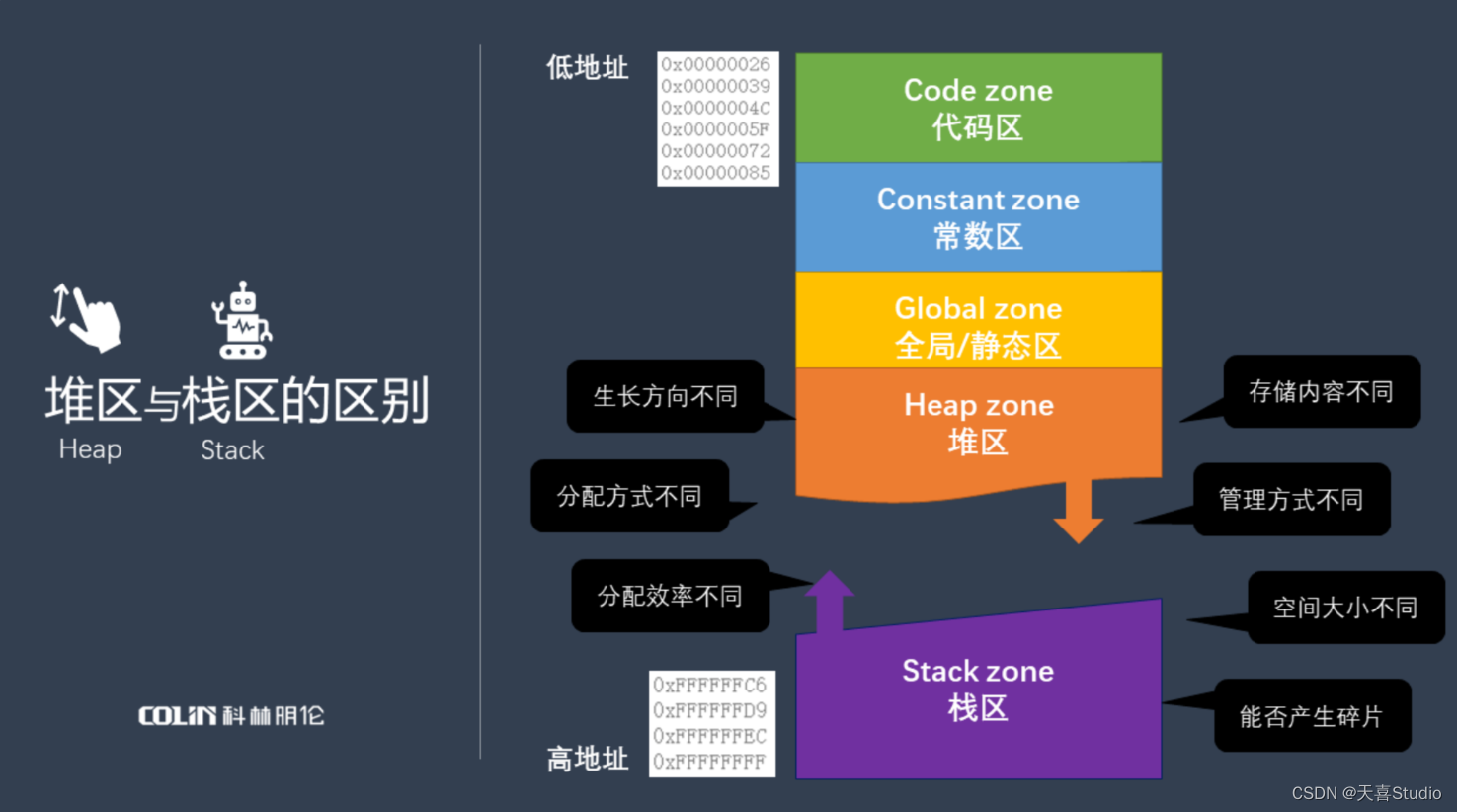
【c语言】五大内存区域 | 堆区详解
创作不易,本篇文章如果帮助到了你,还请点赞支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 给大家跳段街舞感谢支持!ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ…...
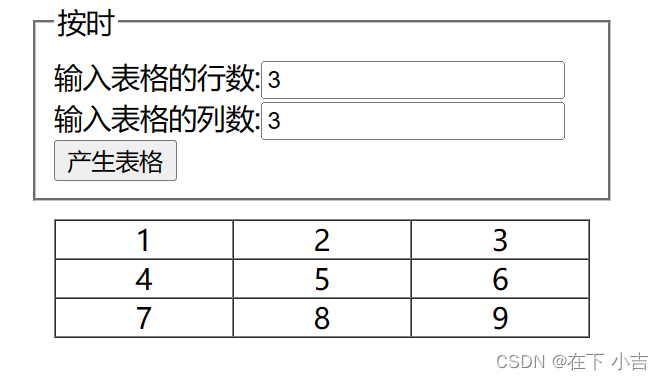
【JavaScript】动态表格
🎊专栏【 前端易错合集】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 大一同学小吉,欢迎并且感谢大家指出我的问题🥰 🍔介绍 就是在输入框中输入数字后,再按…...
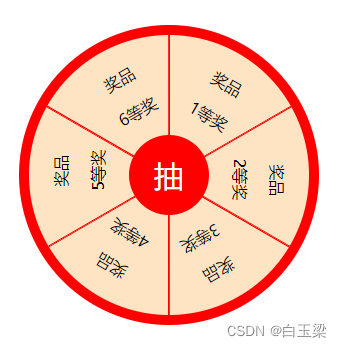
Css如何优雅的实现抽奖转盘
如图,抽奖转盘,可以拆分为几部分: 1.底部大圆; 2.中间小圆; 3.扇形区; 4.扇形内部奖品区; 5.抽奖按钮; 6.点击抽奖按钮时旋转动效及逻辑; 这其中,扇形区&am…...

在Java的小问题
问题1:如何在Java中创建一个对象? 解决方法: 在Java中,要创建一个对象,需要以下步骤: 创建一个类,定义对象的属性和行为。在类中定义一个构造函数,用于初始化对象的属性。在程序中…...
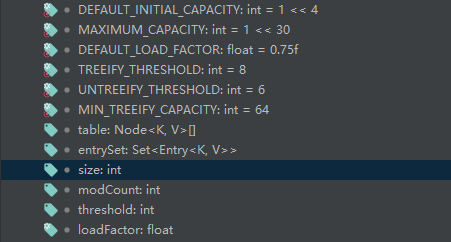
HashMap的扩容机制、初始化容量大小的选择、容量为什么是2的次幂
前置知识 先来看看HashMap中的成员属性 解释: size当前的容器中Entry的数量,也就是当前K-V的数量loadFactory装载因子,用来衡量HashMap满的程度,loadFactory的默认值是0.75threshold临界值,当实际KV数量超过threshol…...
[jenkins自动化2]: linux自动化部署方式之流水线(下篇)
目录 1. 引言: 2. 进阶操作 流水线 -> 2.1 简介: -> 2.2 最终效果图展示: -> 2.3 有没有心动, 真的像流水线一样, 实现了一键部署启动 3. 实现方式 3.1 下载几个插件 3.2 创建流水线任务 3.3 点击配置 3.4 根据流水线语法 写一个简单的helloworld 3.5 执行…...

idea使用 ( 二 ) 创建java项目
3.创建java项目 3.1.创建普通java项目 3.1.1.打开创建向导 接 2.3.1.创建新的项目 也可以 从菜单选择建立项目 会打开下面的选择界面 3.1.2.不使用模板 3.1.3.设置项目名 Project name : 项目名 Project location : 项目存放的位置 确认创建 3.1.4.关闭tips 将 Dont s…...
RabbitMq-接收消息+redis消费者重复接收
在接触RammitMQ时,好多文章都说在配置中设置属性 # rabbitmq 配置 rabbitmq:host: xxx.xxx.xxx.xxxport: xxxxusername: xxxpassword: xxxxxx## 生产端配置# 开启发布确认,就是confirm模式. 消费端ack应答后,才将消息从队列中删除#确认消息已发送到队列(Queue)pub…...
Orangepi Zero2 全志H616简介
为什么学 学习目标依然是Linux 系统 ,平台是 ARM 架构 蜂巢快递柜,配送机器人,这些应用场景用C51,STM32单片机无法实现 第三方介入库的局限性,比如刷脸支付和公交车收费设备需要集成支付宝SDK,提供的libalipay.so 是…...

Golang每日一练(leetDay0047)
目录 138. 复制带随机指针的链表 Copy List with Random-pointer 🌟🌟 139. 单词拆分 Word Break 🌟🌟 140. 单词拆分 II Word Break II 🌟🌟🌟 🌟 每日一练刷题专栏 &…...
HCL Nomad Web 1.0.7发布和新功能验证
大家好,才是真的好。 要问在HCL Notes/Domino系列产品中,谁更新得最快,那么答案一定是HCL Nomad Web。 你看上图右边,从1.0.1更新到1.0.7,都没花多少时间。 从HCL Nomad Web 1.0.5版本开始,可以支持直接…...

春招网申简历填写三技巧
网申第一关很重要,不夸张的说网申决定了你的笔试机会,从如信银行考试中心了解到,银行网申筛选过程中,有机器筛选人工筛选两道程序,掌握填写技巧后对提升简历通过率有较大帮助,一定要把握住,关于…...
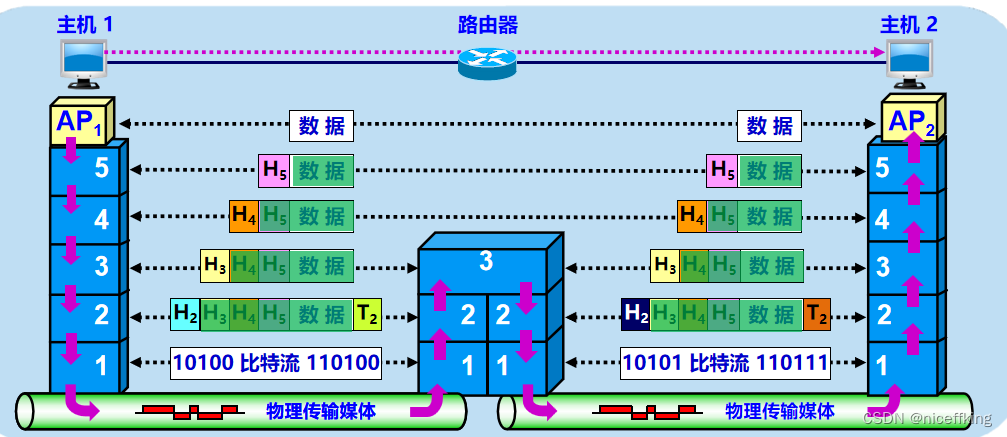
计算机网络基础知识总结
经过学习我们可以知道: 关于计算机网络: ip地址端口号协议协议分层TCP五层协议协议封装两台计算机之间的通信 目录 ip地址 端口号 协议 协议分层 五层协议体系结构 (1) 应用层 (2) 运输层 (3) 网络层 (4)数据链路层 (5)物理层 封装&分用 两台主机之间的通信 …...

(下)苹果有开源,但又怎样呢?
一开始,因为 MacOS X ,苹果与 FreeBSD 过往从密,不仅挖来 FreeBSD 创始人 Jordan Hubbard,更是在此基础上开源了 Darwin。但是,苹果并没有给予 Darwin 太多关注,作为苹果的首个开源项目,它算不上…...

row_number 和 cte 使用实例:考场监考安排
row_number 和 cte 使用实例:考场监考安排 考场监考安排使用 cte 模拟两个表的原始数据使用 master..spt_values 进行数据填充优先安排时长较长的考试使用 cte 安排第一个需要安排的科目统计老师已有的监考时长尝试使用 cte 递归,进行下一场考试安排&…...

2023天梯赛记录
文章目录 L2-001 紧急救援L2-002 链表去重L2-004 这是二叉搜索树吗?L2-005 集合相似度L2-006 树的遍历L2-007 家庭房产L2-010 排座位L2-011 玩转二叉树L2-012 关于堆的判断L2-013 红色警报L2-014 列车调度L2-016 愿天下有情人都是失散多年的兄妹L2-019 悄悄关注L2-0…...
被吐槽 GitHub仓 库太大,直接 600M 瘦身到 6M,这下舒服了
大家好,我是小富~ 前言 忙里偷闲学习了点技术写了点demo代码,打算提交到我那 2000Star 的Github仓库上,居然发现有5个Issues,最近的一条日期已经是2022/8/1了,以前我还真没留意过这些,我这人懒…...
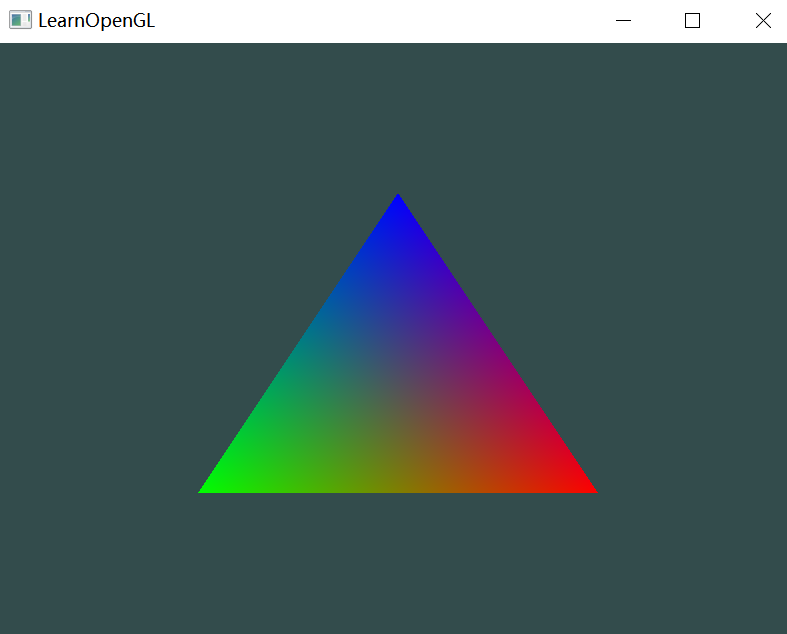
OpenGL(三)——着色器
目录 一、前言 二、Shader 2 Shader 2.1 顶点着色器 2.2 片段着色器 三、APP 2 Shader 四、顶点颜色属性 五、着色器类C 一、前言 着色器Shader是运行在GPU上的小程序,为图形渲染管线的某个特定部分而运行。各阶段着色器之间无法通信,只有输入和输…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

