网络基础-基础网络命令
文章目录
- 路由
- 命令查询
- 添加路由
- 1.添加访问某台主机的静态路由
- 2.添加访问某个网络的静态路由
- 3.添加默认网关:
- 删除
- 设计关键字
- 路由2
- 参考
路由
命令查询
通过 route --help 或man route 查询
添加路由
1.添加访问某台主机的静态路由
route add -host [目标主机IP地址] gw [出口网关]
//我想添加访问192.168.3.100的静态路由,我本机的IP地址是192.168.2.100,默认网关是192.168.2.1,那我可以这样做:
route add -host 192.168.3.100 gw 192.168.2.1
2.添加访问某个网络的静态路由
route add -net [目标网络/子网掩码位数] gw [出口网关]
// 我想添加访问192.168.3.0的静态路由,我本机的IP地址是192.168.2.100,子网掩码是255.255.255.0,默认网关是192.168.2.1,那我可以这样做:
route add -net 192.168.3.0/24 gw 192.168.2.1
3.添加默认网关:
route add default gw [默认网关IP地址]
//我想添加默认网关192.168.2.1,那我可以这样做:
route add default gw 192.168.2.1
删除
删除就是把add 换成del 其余命令不变
设计关键字
route [add|del] [-net|-host] target [netmask Nm] [gw Gw] [[dev] If]
add : 增加路由
del : 删除路由
-net : 设置到某个网段的路由
-host: 设置到某台主机的路由
gw : 出口网关IP地址
dev: 出口网关物理设备名
target : 目的网络或主机
netmask : 目的地址的网络掩码

路由2
通过ip route 添加路由
格式
ip route default via gateway dev interfaceip route ip/netmask(target 网段) via gateway dev interface
via 网关出口 IP地址
dev 网关出口 物理设备名
例如:
参考
Linux 路由 静态路由
相关文章:

网络基础-基础网络命令
文章目录路由命令查询添加路由1.添加访问某台主机的静态路由2.添加访问某个网络的静态路由3.添加默认网关:删除设计关键字路由2参考路由 命令查询 通过 route --help 或man route 查询 添加路由 1.添加访问某台主机的静态路由 route add -host [目标主机IP地址…...

域对象共享数据
处理请求的过程:获取请求参数,调用service处理业务逻辑,往域对象中共享数据,最后实现渲染页面跳转。请求域中共享数据ModelAndView向request域对象共享数据ModelAndView:往域对象共享数据,并实现页面跳转和…...
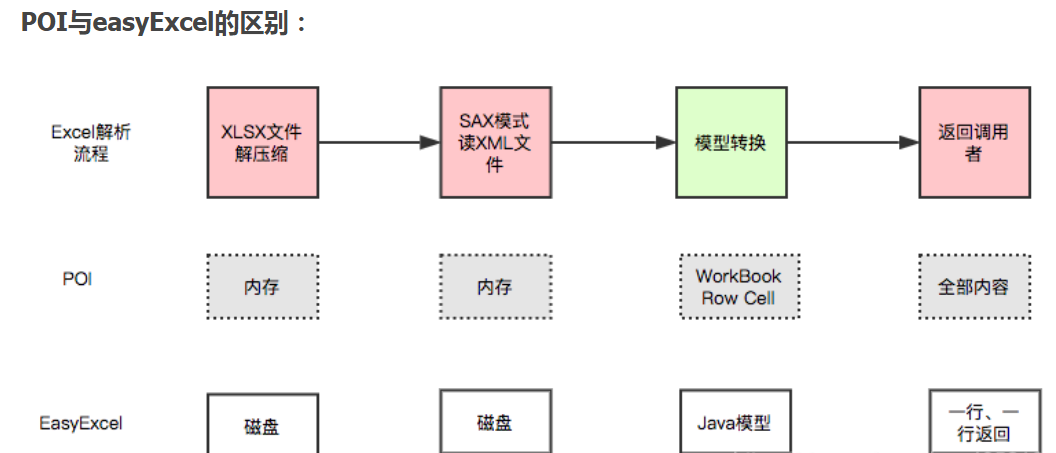
【基于jeeSite框架】SpringBoot+poi+Layui自定义列表导出
文章目录功能效果思路代码前台后台easyPoi,easyExcel,poi三者的区别poipoi依赖导出ExcelHSSF方式导出XSSF方式导出SXSSF方式导出导入excelHSSF方式导入XSSF方式导入SXSSF方式导入easyPoi依赖包采用注解导出导入easyExcel依赖采用注解导出导入API文档easyPoi操作文档…...
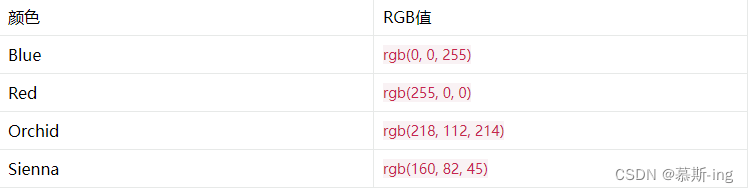
使用 RGB 值设置颜色
使用 RGB 值设置颜色 另一种可以在 CSS 中表示颜色的方法是使用 RGB 值。 RGB 即红色、绿色、蓝色(英语:Red, Green, Blue)。 ● 红色(R)0 到 255 间的整数,代表颜色中的红色成分。。 ● 绿色(G…...

【python学习笔记】:5个高效编程技巧
01 交换变量 >>>a3 >>>b6 这个情况如果要交换变量在c中,肯定需要一个空变量。但是python不需要,只需一行,大家看清楚了 >>>a,bb,a >>>print(a)>>>6 >>&g…...

IP多播技术详解
文章目录前言IP多播技术的相关基本概念IP多播地址和多播组在局域网上进行硬件多播IP多播地址和多播MAC地址映射关系在因特网上进行IP多播网际组管理协议IGMP多播路由选择协议前言 随着计算机网络的发展和个人计算机的普及,人们能够方便的在网络上畅游,进…...
)
华为OD机试真题Python实现【数组排序】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(Python)真题目录汇总华为OD机试(JAVA)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出解题思路核心知识点Python 代码实现代码运行结果版权说明</...

丹麦市政当局通过 NetIQ 身份和访问管理解决方案,提高安全合规性
丹麦市政当局通过 NetIQ 身份和访问管理解决方案,提高安全合规性 概览 公司:普华永道 行业:咨询 地点:丹麦 挑战 创建一个通用框架,以便丹麦市政当局可以无需内部专业知识的前提下利用高级身份和访问管理 使用的…...

内网渗透学习官方文档
内网渗透0x00 kerberos协议0x01 ntlm协议0x02 管道0x03 smb协议0x04 windows访问控制0x05 令牌窃取0x06 SPN扫描&kerberoast0x07 黄金票据0x08 白银票据0x09 MS140680x10 NTDS.DIT && sam0x11 NTLM Relay0x12 MS08-0680x13 CVE-2019-13840x00 kerberos协议 kerber…...

如何编写接口测试用例?
接口测试用例如何编写?下面简单给大家讲解一下。 接口测试用例是目前软件开发中不可或缺的一个重要部分,因此编写接口测试用例同样重要。 接口测试用例的作用非常明显,它能够帮助我们了解产品正在考验、调整它如何表现在特定情境之下、产品是…...

代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ
代码随想录算法训练营第44天 || 完全背包 || 518. 零钱兑换 II || 377. 组合总和 Ⅳ 完全背包 完全背包与01背包的区别在于每种物品都有无限件,可以多次放入背包。 我们回顾一下01背包的遍历顺序,其中内层遍历背包的过程要后序遍历,为什么…...

【Bug】SQL无法绑定由多个部分组成的标识符
文章目录问题原因解决拓展问题 执行sql报:无法绑定由多个部分组成的标识符 原因 取了别名却没用别名,如下面这些情况 select * from biz_production_order_work_detail temp where biz_production_order_work_detail.create_time>2023-02-13selec…...

Games102 学习笔记
Games 102 P2 数据拟合 拟合数据的好坏 分段线性插值函数yf1(x)yf_1(x)yf1(x),数据误差为0,只有C0C_0C0连续。光滑插值函数yf2(x)yf_2(x)yf2(x),数据误差为0,可能被Noice带歪,导致函数性质不好,预…...

知识图谱基本知识点以及应用场景
近两年来,随着Linking Open Data等项目的全面展开,语义Web数据源的数量激增,大量RDF数据被发布。互联网正从仅包含网页和网页之间超链接的文档万维网(Document Web)转变成包含大量描述各种实体和实体之间丰富关系的数据万维网(Data Web)。在这…...

IDEA中常用的快捷键
IDEA中常用的快捷键 自动修正:ALT回车键 代码格式化:CTRLALTL 代码提示:CTRLALT空格 导入当前代码所需要的类:alt回车键 导入当前类中所需要的所有类:ctrlshifto 查看子类:ctrlh 查找类:ctrln …...

朗润国际期货招商:桥水基金四季度投资组合
桥水基金四季度投资组合 总持仓市值183.2亿美元;环比减少7.3% ishares标普500指数ETF:7.93亿占持仓4.33%环比1.14%宝洁:7.57亿占持仓4.13%环比-0.1%新兴市场core TEF-ishares:6.80亿占持仓3.71%环比0.47%强生:6.3亿占…...

Linux管道命令(pipe)全
目录 选取命令:cut、grep 传送门 排序命令:sort、wc、uniq 传送门 双向重定向:tee 字符转换命令:tr、col、join、paste、expand 传送门 划分命令:split 传送门 参数代换:xargs 传送门 关于减号…...

mybatis条件构造器(一)
mybatis条件构造器(一) 1 准备工作 1.1 建表sql语句(Emp表) SET NAMES utf8mb4; SET FOREIGN_KEY_CHECKS 0; -- ---------------------------- -- Table structure for emp -- ---------------------------- DROP TABLE IF EXISTS emp; CREATE TABLE emp (EMPNO int NOT N…...

车联网之电子围栏中ConnectStreamed应用【二十】
文章目录 1. 电子围栏中ConnectStreamed应用1.1 ConnectedStreams简介1.1.1 connect流说明1.1.2 connect流使用场景1.2 Broadcast+Connect+CoFlatmap+CoMap整合实战1.3 两点之间球面距离计算1.4 电子围栏中自定义对象实现CoFlatMap函数1. 电子围栏中ConnectStreamed应用 1.1 C…...

临时文件tempfile
临时文件tempfile 1.概述 安全地创建具有唯一名称的临时文件,以至于他们不会被那些想破坏或者窃取数据的人猜出是非常有挑战性的。tempfile 模块提供了几个安全地创建系统临时文件的方法。 TemporaryFile() 打开并返回一个未命名的临时文件, NamedTemp…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
