机器学习笔记之生成模型综述(四)概率图模型 vs 神经网络
机器学习笔记之生成模型综述——概率图模型vs神经网络
- 引言
- 回顾:概率图模型与前馈神经网络
- 贝叶斯网络 VS\text{VS}VS 神经网络
- 表示层面观察两者区别
- 推断、学习层面观察两者区别
引言
本节将介绍概率图模型与神经网络之间的关联关系和各自特点。
回顾:概率图模型与前馈神经网络
在概率图模型——背景中介绍过,概率图模型不是某一个具体模型,而是一种图结构的统称。而这个图(Graph\text{Graph}Graph)是描述概率模型P(X)\mathcal P(\mathcal X)P(X)内各特征之间关系的一种工具。
也就是说,概率图模型就是 概率模型/概率分布/概率密度函数P(X)\mathcal P(\mathcal X)P(X)的表示(Representation\text{Representation}Representation)。
在前馈神经网络——背景中介绍过,它的核心是通用逼近定理(Universal Approximation Theorem\text{Universal Approximation Theorem}Universal Approximation Theorem),基于该思想,将神经网络视作一个函数逼近器:大于等于一层隐藏层的神经网络可以逼近任意连续函数。
这里的‘神经网络’是指未经修饰的‘前馈神经网络’(Feed-Forward Neural Network\text{Feed-Forward Neural Network}Feed-Forward Neural Network)从‘前馈神经网络’的角度观察,它的任务就是对需要的复杂函数进行拟合,仅此而已。与概率分布没有关联关系。
以前馈神经网络处理亦或分类问题为例,其对应的计算图结构表示如下:
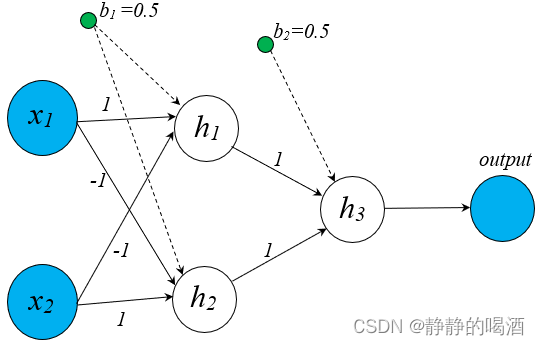
可以看出,这个输出结果output\text{output}output它仅是一个实数,它仅是从计算图结构中通过计算得到的结果而已,并没有概率方面的约束。
因而,但从概率的角度观察,概率图、神经网络是两个独立的概念。但从广义连结主义的角度观察,它们之间确实存在关联关系:
这里为了描述‘神经网络’与概率图结构的各自特点,将关注方向放在贝叶斯网络(Bayessian Network)(\text{Bayessian Network})(Bayessian Network)上,如玻尔兹曼机这种'既属于概率图模型,也属于神经网络'的结构,并不在关注之内。
- 例如玻尔兹曼机为代表的无向图模型。在随机变量结点参数学习的过程中,通常使用马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC\text{Markov Chain Monte Carlo,MCMC}Markov Chain Monte Carlo,MCMC)、变分推断(Variational Inference,VI\text{Variational Inference,VI}Variational Inference,VI)这种方式进行求解。针对这种基于随机采样对模型参数近似求解的结构,被称为随机神经网络(Stochastic Neural Network\text{Stochastic Neural Network}Stochastic Neural Network)。
- 相反,通过计算图来实现模型参数的精确求解,如前馈神经网络以及其变种结构如卷积神经网络(Convolutional Neural Networks, CNN\text{Convolutional Neural Networks, CNN}Convolutional Neural Networks, CNN),循环神经网络(Recurrent Neural Network, RNN\text{Recurrent Neural Network, RNN}Recurrent Neural Network, RNN)等等,被称之为确定性神经网络(Deterministic Neural Network\text{Deterministic Neural Network}Deterministic Neural Network)。
贝叶斯网络 VS\text{VS}VS 神经网络
这里依然从表示(Representation\text{Representation}Representation)、推断(Inference\text{Inference}Inference)、学习(Learning\text{Learning}Learning)三个角度对贝叶斯网络与神经网络之间进行比较:
这里的‘神经网络’具体指‘确定性神经网络’;‘概率图模型’具体指‘贝叶斯网络’。
从概率图与计算图的角度观察,概率图描述的是模型本身;而计算图仅构建了一个函数逼近的计算流程,计算图自身没有建模意义。但可以像生成对抗网络一样,将计算图本身看作一个复杂函数,进行建模。
表示层面观察两者区别
在介绍之前,我们介绍过Sigmoid\text{Sigmoid}Sigmoid信念网络,虽然它是一个典型的有向图模型,但它依然是通过醒眠算法(Wake-Sleep Algorithm\text{Wake-Sleep Algorithm}Wake-Sleep Algorithm)——通过采样的方式对模型参数进行近似学习。因此它也是一个随机神经网络,不在考虑之内。
贝叶斯网络的特点有:浅层、稀疏化、结构化。
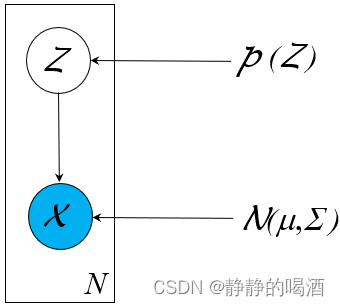
‘稀疏化’具体是通过人为的一系列条件独立性假设来约束结点之间的连接关系,主要是为了简化运算。如朴素贝叶斯分类器中的‘朴素贝叶斯假设’;隐马尔可夫模型中的‘齐次马尔可夫假设’与‘观测独立性假设’都属于使概率图结构稀疏化的假设。‘浅层’是指计算结点没有堆叠现象。与生成模型综述中介绍的‘深度生成模型’有少许区别。深度生成模型中的计算结点指的就是随机变量(隐变量、观测变量);而这里的计算结点有可能是随机变量结点,也可能是神经网络中的神经元结点。‘结构化’是指针对某种具体任务,人为地设置成某种特定结构的格式。例如高斯混合模型,它被设置成这种结构去处理聚类任务:
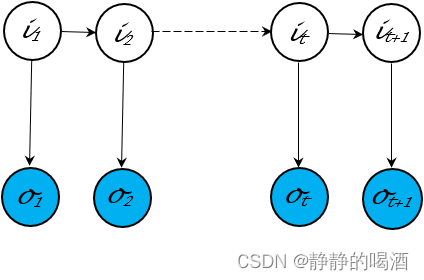
再例如隐马尔可夫模型,这种概率图结构被设计处理状态序列预测问题:
与之相对的,神经网络的特点:深层、稠密。
这里的‘深层’是指神经网络中隐藏层的数量。针对逼近函数的复杂程度,可以通过增加隐藏层的方式对输入特征进行更深层次地学习;
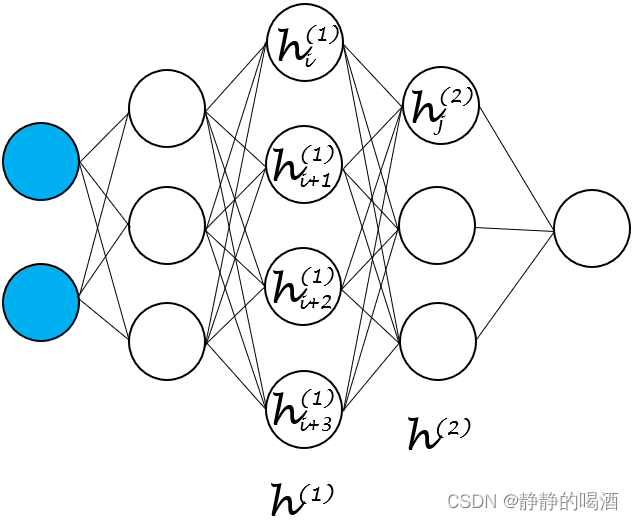
‘稠密’是指层与层神经元结点之间的关联关系是随意的,未被条件独立性约束的。
并且神经网络中的节点指的是计算图(Computational Graph\text{Computational Graph}Computational Graph)中的计算结点,相比于随机变量结点,如隐变量结点。我们并没有给计算节点针对图结构赋予相应的实际意义。
或者说,神经网络中的隐藏层单元是否有解释性并不重要,无论是哪种前馈神经网络,隐藏层单元的意义就只有‘逼近复杂函数过程中的一个环节’而已。
层与层之间关联关系表示如下(以上述h(2)h^{(2)}h(2)层计算节点hj(2)h_j^{(2)}hj(2)为例):
通过h(1)h^{(1)}h(1)层中的hi(1),hi+1(i),hi+2(1),hi+3(1)h_{i}^{(1)},h_{i+1}^{(i)},h_{i+2}^{(1)},h_{i+3}^{(1)}hi(1),hi+1(i),hi+2(1),hi+3(1)与对应权重参数的线性组合后关于激活函数Sign\text{Sign}Sign的映射结果,b(1)b^{(1)}b(1)表示h(1)h^{(1)}h(1)层对应的偏置信息。
hj(2)=Sign([W(1)]Th(1)+b(1))=Sign([Wi(1)]Thi(1)+[Wi+1(1)]Thi+1(1)+[Wi+2(1)]Thi+2(1)+[Wi+3(1)]Thi+3(1)+b(1))\begin{aligned} h_j^{(2)} & = \text{Sign}\left([\mathcal W^{(1)}]^T h^{(1)} + b^{(1)}\right) \\ & = \text{Sign} \left([\mathcal W_i^{(1)}]^Th_i^{(1)} + [\mathcal W_{i+1}^{(1)}]^Th_{i+1}^{(1)} + [\mathcal W_{i+2}^{(1)}]^Th_{i+2}^{(1)} + [\mathcal W_{i+3}^{(1)}]^Th_{i+3}^{(1)} + b^{(1)}\right) \end{aligned}hj(2)=Sign([W(1)]Th(1)+b(1))=Sign([Wi(1)]Thi(1)+[Wi+1(1)]Thi+1(1)+[Wi+2(1)]Thi+2(1)+[Wi+3(1)]Thi+3(1)+b(1))
基于上述描述,可以看出,关于贝叶斯网络概率图结构中结点之间的关联关系(有向边)是可解释的(Meaningful\text{Meaningful}Meaningful):而这个解释就是基于某随机变量结点条件下,其他结点发生的条件概率。如齐次马尔可夫假设,观测独立性假设:
无论是观测变量结点,还是隐变量结点,在建模过程中均基于实际任务赋予了物理意义。
{P(it+1∣it,⋯,i1,o1,⋯,ot)=P(it+1∣it)P(ot∣it,⋯,i1,ot−1,⋯,o1)=P(ot∣it)\begin{cases} \mathcal P(i_{t+1} \mid i_t,\cdots,i_1,o_1,\cdots,o_t) = \mathcal P(i_{t+1} \mid i_t)\\ \mathcal P(o_t \mid i_t,\cdots,i_1,o_{t-1},\cdots,o_1) = \mathcal P(o_t \mid i_t) \end{cases}{P(it+1∣it,⋯,i1,o1,⋯,ot)=P(it+1∣it)P(ot∣it,⋯,i1,ot−1,⋯,o1)=P(ot∣it)
推断、学习层面观察两者区别
如果是概率图模型,它的推断方式多种多样。在概率图模型——推断基本介绍中提到过,推断本质上就是 基于给定的模型参数,对随机变量的概率进行求解。
- 这里的随机变量指的可能是观测变量,也可能是隐变量;
- 这里的概率指的可能是边缘概率,也可能是条件概率,也可能是联合概率(概率密度函数)。
推断选择的方式也根据随机变量的性质(复杂程度:随机变量离散/连续;概率分布:简单/复杂)可进行选择。常见的推断方式有如下几种:
- 精确推断:如变量消去法(Variable Elimination,VE\text{Variable Elimination,VE}Variable Elimination,VE)。其本质上是基于概率图结构对无效的条件概率进行消除,从而达到简化运算的目的。例如某贝叶斯网络表示如下:
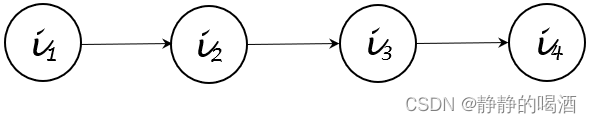
根据其拓扑排序顺序,可将上述概率图i4i_4i4结点的边缘概率分布P(i4)\mathcal P(i_4)P(i4)化简为如下形式:
原始方法与变量消去法之间进行对比。
{Original Method: P(i4)=∑i1,i2,i3P(i1,i2,i3,i4)=∑i1,i2,i3P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)VE Method: P(i4)=∑i1,i2,i3P(i1,i2,i3,i4)=∑i3P(i4∣i3)⋅∑i2P(i3∣i2)⋅∑i1P(i2∣i1)⋅P(i1)\begin{cases} \text{Original Method: }\begin{aligned}\mathcal P(i_4) &= \sum_{i_1,i_2,i_3} \mathcal P(i_1,i_2,i_3,i_4) \\ & = \sum_{i_1,i_2,i_3} \mathcal P(i_1) \cdot \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_3 \mid i_2) \cdot \mathcal P(i_4 \mid i_3) \end{aligned} \\ \text{VE Method: } \quad \quad \begin{aligned} \mathcal P(i_4) & = \sum_{i_1,i_2,i_3} \mathcal P(i_1,i_2,i_3,i_4) \\ & = \sum_{i_3} \mathcal P(i_4 \mid i_3) \cdot \sum_{i_2} \mathcal P(i_3 \mid i_2) \cdot \sum_{i_1} \mathcal P(i_2 \mid i_1) \cdot \mathcal P(i_1) \end{aligned} \end{cases}⎩⎨⎧Original Method: P(i4)=i1,i2,i3∑P(i1,i2,i3,i4)=i1,i2,i3∑P(i1)⋅P(i2∣i1)⋅P(i3∣i2)⋅P(i4∣i3)VE Method: P(i4)=i1,i2,i3∑P(i1,i2,i3,i4)=i3∑P(i4∣i3)⋅i2∑P(i3∣i2)⋅i1∑P(i2∣i1)⋅P(i1)
同理,精确推断还有基于前向后向算法逻辑的信念传播(Belief Propagation,BP)方法。 - 近似推断(Approximate Inference\text{Approximate Inference}Approximate Inference):针对随机变量结点的概率无法准确求解/求解代价极大。最典型的依然是因隐变量Z\mathcal ZZ维度过高产生的 积分难问题:
P(X)=∫z1⋯∫zKP(X∣Z)⋅P(Z)dz1,⋯,zK\begin{aligned} \mathcal P(\mathcal X) = \int_{z_1} \cdots\int_{z_{\mathcal K}} \mathcal P(\mathcal X \mid \mathcal Z) \cdot \mathcal P(\mathcal Z) dz_1,\cdots,z_{\mathcal K} \end{aligned}P(X)=∫z1⋯∫zKP(X∣Z)⋅P(Z)dz1,⋯,zK
对应采样方法如变分推断(Variational Inference,VI\text{Variational Inference,VI}Variational Inference,VI),以及基于采样方式的随机性近似方法:马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC\text{Markov Chain Monte Carlo,MCMC}Markov Chain Monte Carlo,MCMC)。
从学习层面观察,由于是基于概率分布,因而关于模型参数学习的底层方法是极大似然估计(Maximum Likelihood Estimatation,MLE\text{Maximum Likelihood Estimatation,MLE}Maximum Likelihood Estimatation,MLE)。
当然,这仅是常规的学习思路。其他方法例如以生成对抗网络(Generative Adversarial Networks,GAN\text{Generative Adversarial Networks,GAN}Generative Adversarial Networks,GAN)为代表的对抗学习等。
例如高斯混合模型、隐马尔可夫模型中使用的EM\text{EM}EM算法,它们都是极大似然估计的衍生方法。
而神经网络中不存在推断一说。
- 隐藏层神经元结点产生的中间值仅仅表示一个实数,连基本的概率意义都没有。自然不会出现隐藏层关于某神经元结点的概率这种描述。
- 和上述的前馈神经网络处理 亦或问题 一样,一旦权重W\mathcal WW、偏置信息bbb给定的条件下,给定一个输入,那么神经网络中所有隐藏层结点结果均被固定,不存在不确定的分布一说。
关于神经网络的学习任务相比于概率图模型单调一些。其核心是梯度下降方法(Gradient Descent,GD\text{Gradient Descent,GD}Gradient Descent,GD)。
无论是随机梯度下降(Stochastic Gradient Descent,SGD\text{Stochastic Gradient Descent,SGD}Stochastic Gradient Descent,SGD),批量梯度下降(Batch Gradient Descent,BGD\text{Batch Gradient Descent,BGD}Batch Gradient Descent,BGD),RMSProp\text{RMSProp}RMSProp,Adagrad\text{Adagrad}Adagrad,Adam\text{Adam}Adam算法,其底层逻辑均属于梯度下降方法。详细可参阅这篇文章,非常感谢。传送门
如果神经网络内隐藏层数量较多,梯度求解过程复杂,则引入反向传播算法(Backward Propagation,BP\text{Backward Propagation,BP}Backward Propagation,BP)
需要注意的是,反向传播算法只是一种‘高效的求导方法’,这种方法仅是在每次迭代过程中将梯度传递给各个隐藏层神经元的权重信息中,它本身并不是参数学习方法。
相关参考:
【pytorch】3.0 优化器BGD、SGD、MSGD、Momentum、Adagrad、RMSPprop、Adam
生成模型5-概率图VS神经网络
相关文章:

机器学习笔记之生成模型综述(四)概率图模型 vs 神经网络
机器学习笔记之生成模型综述——概率图模型vs神经网络引言回顾:概率图模型与前馈神经网络贝叶斯网络 VS\text{VS}VS 神经网络表示层面观察两者区别推断、学习层面观察两者区别引言 本节将介绍概率图模型与神经网络之间的关联关系和各自特点。 回顾:概率…...

微信小程序 组件与页面交互 无反应的问题
使用组件 声明组件 1.在目录中右键,新建components 2.在页面的json,属性中加入"component": true, 编写组件 父 声明: "usingComponents": {"address": "../../components/address/address"},…...

maven相关概念以及no dependency information available错误修改
一,相关概念 1,Maven坐标 Maven定义了这样一组规则:世界上任何一个构件都可以使用Maven坐标唯一标识,Maven坐标元素包括groupId、artifactId、version、packaging、classifier,现在只要我们提供正确的元素坐标&#x…...

QML- 属性绑定
QML- 属性绑定一、概述二、 QML绑定使用三、从JavaScript创建属性绑定1. 调试绑定的覆盖2. 属性绑定使用 this一、概述 QML对象的属性可以被赋一个静态值,该值保持不变,直到显式地赋一个新值。但是,为了充分利用QML及其对动态对象行为的内置…...

MFC CObject的使用
目录1 从 CObject 派生类1.1 使用基本 CObject 功能1.2 添加运行时类信息1.3 添加动态创建支持1.4 添加序列化支持2 访问运行时类信息3 动态对象创建1 从 CObject 派生类 在 CObject 的讨论中,经常使用术语“接口文件”和“实现文件”。 接口文件(通常称…...
Calico 介绍与原理(一))
CNI 网络流量分析(六)Calico 介绍与原理(一)
文章目录CNI 网络流量分析(六)Calico 介绍与原理(一)介绍安装Calico-node初始化Calico-node 服务Felixconfdallocate-tunnel-addrsmonitor-addressesmonitor-tokenstatus-reporterbirdcalico-kube-controllersCNI 网络流量分析&am…...

机器视觉_HALCON_示例实践_1.检测圆形
文章目录一、引言二、检测圆形三、总结一、引言 前面的文(用户指南/快速向导)差不多已经把HALCON的基本内容讲完了,并且在学习过程中还跑过一个简单示例——在单一背景下定位回形针。示例跑过,顿时觉得自己行了,但如果…...
使用yolov5训练数据集笔记
准备工作 1. 安装labelimg labelimg:主要用于目标检测的目标框绘制,得到关于我们训练的边框位置、类别等数据 pip install labelimg2. 下载yolov5源码 我使用的是v7.0版本,直接下载即可,下载后解压出来 2.1 安装yolov5运行依赖包 进入…...
常用类详解(三)StringBuilder
(1)一个可爱的字符序列。此类提供一个与StringBuffer兼容的API,但不保证同步(StringBuilder不是线程安全的),该类被设计用作StringBuffer的一个简易替换,用在字符串缓冲区被单个线程使用的时候。如果可能,建议优先采用该类&#x…...

OpenCV 文字绘制----cv::putText详解
opencv中除了提供绘制各种图形的函数外,还提供了一个特殊的绘制函数——在图像上绘制文字。这个函数cv::putText()。 具体形式如下: void cv::putText( cv::Mat& img, // 待绘制的图像 const string& text, // 待绘制的文字 cv::Point origin…...

同IP多个端口域名同时进行目录爆破
背景 目录爆破是信息收集不可缺的一部分 在渗透过程中,扫描地址时发现同IP下存在多个端口,且每个端口均属于域名,仅仅端口号不同 需求 同一个IP下,同时收集多个不同端口的域名目录爆破进行信息收集,且简单便捷(一行代码) 用到的工具 gobuster 下载地址:https://…...

react+antd+Table里切换Switch改变状态onChange 传参
场景:table列表里面,操作用Switch切换状态。对应列改变操作在colums里面// 表格行const colums: ColumnsType<potentialType> [{title: useLocale(创建时间),dataIndex: creation_date,key: creation_date,align: center,render: (v: string, rec…...

《底层逻辑:看清这个世界的底牌》读后感
书名《底层逻辑:看清这个世界的底牌》作者刘润简介如果只教给你各行各业的“干货”(方法论),那只是“授人以鱼”,一旦环境出现任何变化,“干货”就不再适用。但如果教给你的是底层逻辑,那就是“…...
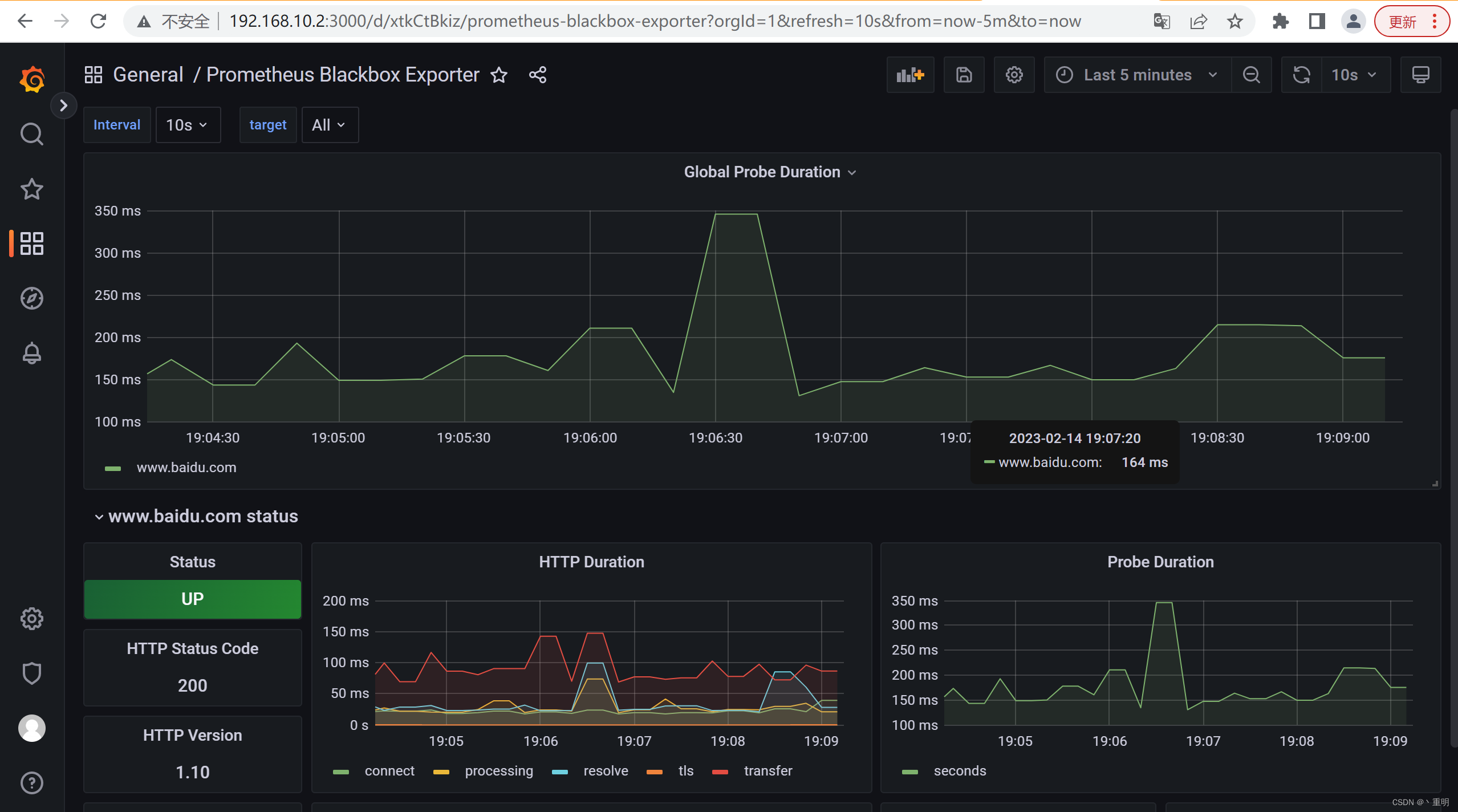
【2023】Prometheus-Blackbox_exporter使用
目录1.下载及安装blackbox_exporter2.修改配置文件设置监控内容2.1.使用http方式作为探测3.与prometheus集成4.导入blackbox仪表盘进行观测1.下载及安装blackbox_exporter 下载安装包 wget https://github.com/prometheus/blackbox_exporter/releases/download/v0.23.0/black…...

嵌入式Linux学习经典书籍-学完你就是高手
很多刚入门的朋友一直都有人问我要学习资料,嵌入式实在太杂,网上很多人写的太不负责了,本书单综合了本人以及一些朋友多年的经验整理而成。 本人见识和阅读量有限,本书单可能有不对的地方,欢迎朋友指正,交…...

网络基础-基础网络命令
文章目录路由命令查询添加路由1.添加访问某台主机的静态路由2.添加访问某个网络的静态路由3.添加默认网关:删除设计关键字路由2参考路由 命令查询 通过 route --help 或man route 查询 添加路由 1.添加访问某台主机的静态路由 route add -host [目标主机IP地址…...

域对象共享数据
处理请求的过程:获取请求参数,调用service处理业务逻辑,往域对象中共享数据,最后实现渲染页面跳转。请求域中共享数据ModelAndView向request域对象共享数据ModelAndView:往域对象共享数据,并实现页面跳转和…...
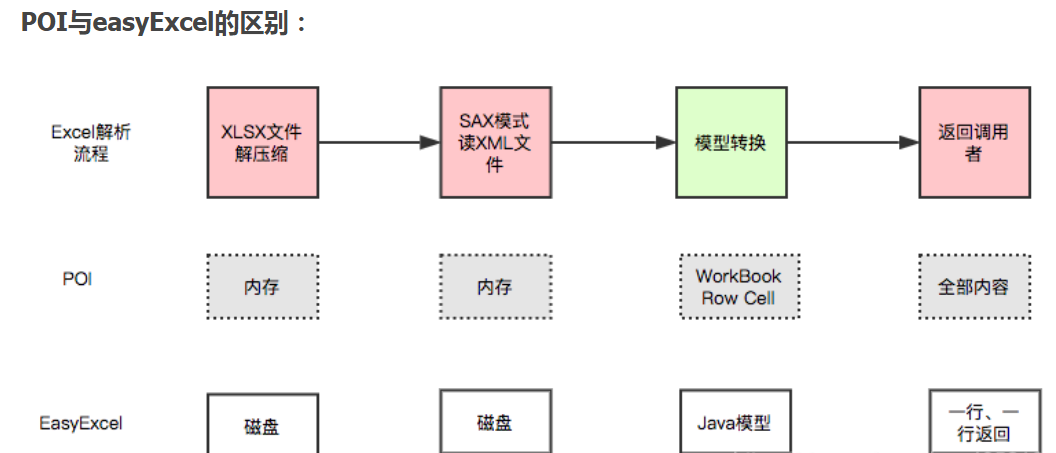
【基于jeeSite框架】SpringBoot+poi+Layui自定义列表导出
文章目录功能效果思路代码前台后台easyPoi,easyExcel,poi三者的区别poipoi依赖导出ExcelHSSF方式导出XSSF方式导出SXSSF方式导出导入excelHSSF方式导入XSSF方式导入SXSSF方式导入easyPoi依赖包采用注解导出导入easyExcel依赖采用注解导出导入API文档easyPoi操作文档…...
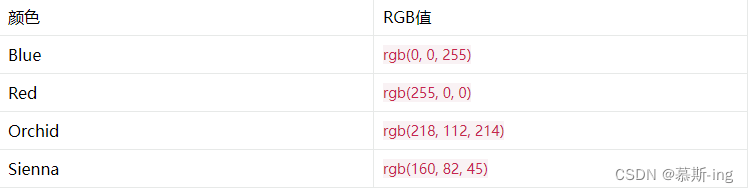
使用 RGB 值设置颜色
使用 RGB 值设置颜色 另一种可以在 CSS 中表示颜色的方法是使用 RGB 值。 RGB 即红色、绿色、蓝色(英语:Red, Green, Blue)。 ● 红色(R)0 到 255 间的整数,代表颜色中的红色成分。。 ● 绿色(G…...

【python学习笔记】:5个高效编程技巧
01 交换变量 >>>a3 >>>b6 这个情况如果要交换变量在c中,肯定需要一个空变量。但是python不需要,只需一行,大家看清楚了 >>>a,bb,a >>>print(a)>>>6 >>&g…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
