【算法】【算法杂谈】从M个数中等概率的选出n个数,保证每一个数的选中概率都是n/m(蓄水池算法)
目录
- 前言
- 问题介绍
- 解决方案
- 代码编写
- java语言版本
- c语言版本
- c++语言版本
- 思考感悟
- 写在最后
前言
当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~
在此感谢左大神让我对算法有了新的感悟认识!
问题介绍
原问题
存在一个吐球的机器,该机器吐球的顺序是 : 1号球,2号球,3号球…m号球,一共吐m个求
现在你有一个袋子,大小是n,n<m,当m个球吐完之后,你的袋子中应该有n个球,那么现在设计一个算法保证袋子中的n个球每一个球进入袋子中的概率都是相等的,都是n/m
解决方案
原问题:
解法很简单,证明在后面:
1、首先创建一个数组作为“袋子”,用来获取等概率的结果
2、循环将球放入袋子,在袋子装满之前,所有球都放入袋子
3、如果袋子满了,此时为第i个球,判断rand(i)是否大于n,如果小于袋子的大小,则随机找袋子中的某个位置覆盖,否则不放入
4、循环完成即可,此时袋子中每一个球放入的概率都是n/m
代码编写
java语言版本
原问题:
方法一:
/*** 二轮测试:蓄水池算法* @param k* @param max* @return*/public static int[] getKNumRandCp1(int k, int max) {int[] container = new int[k];// 初始化//for (int i = 0; i < max; i++) {// container[i] = i + 1;//}for (int i = 0; i < max; i++) {if (i < k) {container[i] = i + 1;continue;}// 如果随机数没有超过k,则随机替换一个if (rand(i) <= k) {container[randCp1(k) - 1] = i;}}return container;}public static int randCp1(int num) {return (int)(Math.random() * num + 1);}public static void main(String[] args) {CommonUtils.printArr(getKNumRandCp1(5, 9));}c语言版本
正在学习中
c++语言版本
正在学习中
思考感悟
如果不看证明我其实不知道为什么这样就一定是等概率的。
然后看了书里面的概率计算公式之后算是有些明白了:
首先我们看看第i号球如何才能被选中踢出去被n+1号球替换:
首先要满足两个条件:1、rand(n+1) < n 2、rand(n) = i
那么这两个事件的概率乘积就是i被k+1号球替换的概率:n/(n+1) * (1/n)
那么反过来,i球留下来的概率就是 1- 1/(n+1) = nn+1
同理可以计算出没有被n+2,n+3换出来的概率
n+2 : (n+1)/(n+2)
n+3 : (n+2)/(n+3)
ok,如果在每一轮的随机下,最终i球留下来没有被替换出去,那么就算是i球被选中了,所以接下来我们求n轮后i号球留下来的概率即可
也就是从n+1一直到m,所有没有被换出去的概率乘积
n/n+1 * (n+1)/(n+2) * (n+2)/(n+3) … (m-1)/m= n/ m
这个概率刚好是等概率替换的概率,完美的证明~
写在最后
方案和代码仅提供学习和思考使用,切勿随意滥用!如有错误和不合理的地方,务必批评指正~
如果需要git源码可邮件给2260755767@qq.com
再次感谢左大神对我算法的指点迷津!
相关文章:
)
【算法】【算法杂谈】从M个数中等概率的选出n个数,保证每一个数的选中概率都是n/m(蓄水池算法)
目录 前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本 思考感悟写在最后 前言 当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介…...
vue3+ts+vite自适应项目——路由、layout布局
系列文章目录 第一章:搭建项目 目录 系列文章目录 前言 一、vue-router 1.安装vue-router 2.引入 2.1 新建页面 2.2 公共样式引入 2.3 layout 布局 2.4路由配置 总结 前言 上一章我们搭建了项目,这一张主要讲路由和layout布局,和…...
数据库之约束、索引和事务
一、约束 约束,顾名思义就是数据库对数据库中的数据所给出的一组检验规则.负责判断元素是否符合数据库要求.其目的就是为了提高效率以及准确性. 1.not null - > 数据元素非空 表示如果插入数据,则当前数据不能为空. //创建一张学生表,其班级id和年级id不为空 create …...

centos --libreoffice使用
您可以按照以下步骤在CentOS上安装LibreOffice: 打开终端并使用root用户登录。 运行以下命令更新系统软件包: yum update安装LibreOffice依赖项: yum install -y libreoffice-headless libreoffice-writer libreoffice-calc libreoffice-…...

Steam-V Rising 私人服务器架设教程
一、安装前的准备 一台服务器 拥有公网IP并且做好了端口映射 二、使用SteamCMD安装服务器 1.下载SteamCMD SteamCMD是Steam专用的命令行式客户端程序,所有的安装方式可以参照:https://developer.valvesoftware.com/wiki/SteamCMD 或者在其他站点自行…...

SpringBoot+Vue3实现登录验证码功能
系列文章目录 Redis缓存穿透、击穿、雪崩问题及解决方法Spring Cache的使用–快速上手篇分页查询–Java项目实战篇全局异常处理–Java实战项目篇 Java实现发送邮件(定时自动发送邮件)_java邮件通知_心态还需努力呀的博客-CSDN博客 该系列文章持续更新…...
spring2:创建和使用
目录 1.创建Spring项目 1.1创建Maven类 1.2添加Spring支持框架 1.3添加启动类 2.存储Bean对象 2.0 spring项目中添加配置文件(第一次) 2.1创建Bean 2.2把Bean注册到容器中 3.获取并使用Bean对象 3.1创建上下文 3.2获取指定Bean对象 getBean()方法 --> 获取什么…...

前端如何处理后端一次性传来的10w条数据?
写在前面 如果你在面试中被问到这个问题,你可以用下面的内容回答这个问题,如果你在工作中遇到这个问题,你应该先揍那个写 API 的人。 创建服务器 为了方便后续测试,我们可以使用node创建一个简单的服务器。 const http requir…...
Codeforces Round 867 (Div. 3)(A-G2)
文章目录 A. TubeTube Feed1、题目2、分析3、代码, B. Karina and Array1、题目2、分析3、代码 C. Bun Lover1、问题2、分析(1)观察样例法(2)正解推导 3、代码 D. Super-Permutation1、问题2、分析(1&#…...

蓝奥声核心技术分享——一种无线低功耗配置技术
1.技术背景 无线低功耗配置技术指基于对目标场景状态变化的协同感知而获得触发响应并进行智能决策,属于蓝奥声核心技术--边缘协同感知(EICS)技术的关键支撑性技术之一。该项技术涉及物联网边缘域的无线通信技术领域,具体主要涉及网络服务节点…...

kafka集群模拟单节点故障
这里通过kafka manage来展示节点宕机效果 现在三台主机节点均正常 topic正常识别到三个broker leader也均匀分配到了三个broker上 现在把节点id为0的主机模拟宕机 可以通过以上两张图片看到每个topic现在只识别到了两个broker节点,broker id为0的节点已经被剔除掉了 isr列…...

笔记:vue-cli-service
vue-cli-service serve 这个是什么意思? vue-cli-service serve 是一个 Vue.js CLI 命令,用于在本地开发环境下运行一个开发服务器,以便你可以在浏览器中查看和测试你的 Vue.js 应用程序。它在开发期间提供了自动重载、热模块替换和其它实用…...
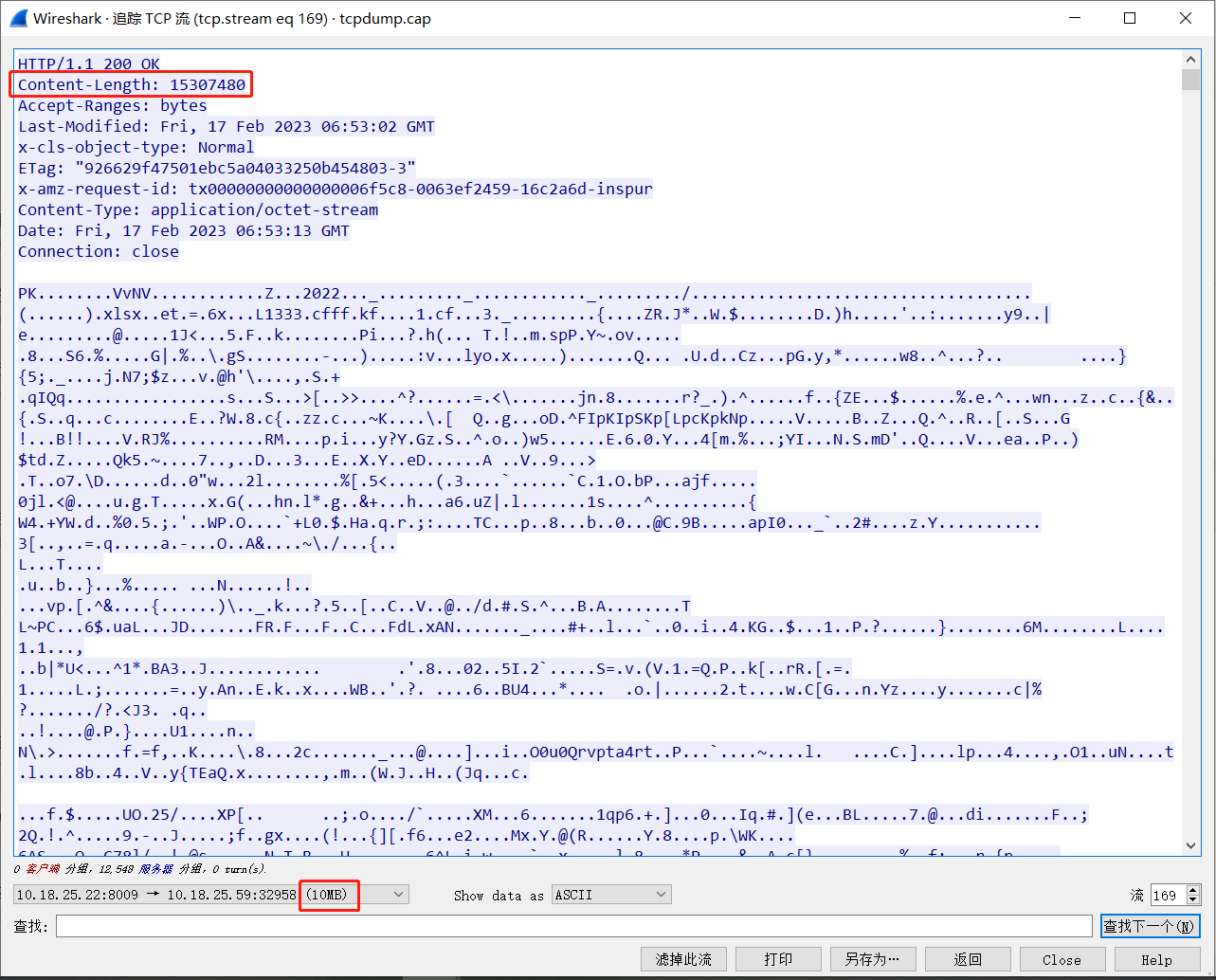
Amazon S3 对象存储Java API操作记录(Minio与S3 SDK两种实现)
缘起 今年(2023年) 2月的时候做了个适配Amazon S3对象存储接口的需求,由于4月份自学考试临近,一直在备考就拖着没总结记录下,开发联调过程中也出现过一些奇葩的问题,最近人刚从考试缓过来顺手记录一下。 S3对象存储的基本概念 …...

ChatGPT技术原理 第六章:对话生成技术
目录 6.1 任务定义 6.2 基于检索的方法 6.3 基于生成的方法 6.4 评价指标 6.1 任务定义 对话生成技术是指使用自然语言处理技术生成与人类语言相似的对话。在对话生成任务中,模型需要理解输入的语境、用户的意图和上下文信息,然后生成能够回答用户问题…...

【C++ 八】写文件、读文件
写文件、读文件 文章目录 写文件、读文件前言1 文本文件1.1 写文件1.2 读文件 2 二进制文件2.1 写文件2.2 读文件 前言 本文包含文本文件写文件、文本文件读文件、二进制写文件、二进制读文件。 程序运行时产生的数据都属于临时数据,程序一旦运行结束都会被释放 通…...

【学习笔记】CF613E Puzzle Lover
这题本质上还是数据结构。 首先看到这个 2 n 2\times n 2n的网格图就很容易想到分治。我们还是考虑把要统计的东西变得可视化,一条路径要么穿过中线一次,那么我们可以将两边的串拼起来得到答案;要么穿过中线两次,考虑其中一边的…...

软考报名资格审核要多久?证明材料要哪些?
软考报名资格审核要多久? 一般来说,软考资格审核时间不超过1个工作日。当然,每个地区的具体情况都不一样。有些地区估计需要1-3个工作日。总之,为了顺利成功报名,大家应尽快报名,不要拖到最后一天。 软考…...

2023-04-27 polardbx-LSM-tree的Parallel Recovery性能优化
背景 数据库的Crash Recovery时长关系到数据库的可用性SLA、故障止损时间、升级效率等多个方面。本文描述了针对X-Engine数据库存储引擎的一种Crash Recovery优化手段,在典型场景下可以显著缩短数据库实例的故障恢复时间,提升用户使用感受。 当前面临的问题 X-Engine是阿里…...

创作纪念日让 AI 与我共同记录下今天 — 【第五周年、1460天】
今天正是五一,收到一条消息? 五一还要我加班 😏? 喔,原来是 CSDN 给我发的消息呀!我在 CSDN 不知不觉已经开启第五周年啦! 目录 1.机缘2.收获3.日常4.我与 AI 的“合作”part Ipart II Super al…...

枚举法计算24点游戏
# 请在此处编写代码 # 24点游戏 import itertools# 计算24点游戏代码 def twentyfour(cards):"""(1)itertools.permutations(可迭代对象):通俗地讲,就是返回可迭代对象的所有数学全排列方式。itertools.permutations("1118") -…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
