( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II
难度:中等
给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件:
假设该列表是 answer = [a1, a2, a3, ... , an] ,那么列表 [|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|] 中应该有且仅有 k 个不同整数。
返回列表 answer 。如果存在多种答案,只需返回其中 任意一种 。
示例 1:
输入:n = 3, k = 1
输出:[1, 2, 3]
解释:[1, 2, 3] 包含 3 个范围在 1-3 的不同整数,并且 [1, 1] 中有且仅有 1 个不同整数:1
示例 2:
输入:n = 3, k = 2
输出:[1, 3, 2]
解释:[1, 3, 2] 包含 3 个范围在 1-3 的不同整数,并且 [2, 1] 中有且仅有 2 个不同整数:1 和 2
提示:
- 1 < = k < n < = 1 0 4 1 <= k < n <= 10^4 1<=k<n<=104
💡思路:
当 k=1 时,我们将 1∼n 按照 [1,2,⋯ ,n]的顺序进行排列,那么相邻的差均为 1,满足 k=1 的要求。
当 k=n−1 时,我们将 1∼n 按照 [1, n, 2, n−1, 3, ⋯ ]的顺序进行交叉排列,那么相邻的差从 n−1 开始,依次递减 1。这样一来,所有从 1 到 n−1的差值均出现一次,满足 k = n−1的要求。
所以对于其它的一般情况,我们可以将这两种特殊情况进行合并,即列表的前半部分相邻差均为 1,后半部分相邻差从 k 开始逐渐递减到 1,这样从 1 到 k 的差值均出现一次,对应的列表即为
[ 1 , 2 , ⋯ , n − k , n , n − k + 1 , n − 1 , n − k + 2 , ⋯ ] [1,2,⋯,n−k,n,n−k+1,n−1,n−k+2,⋯] [1,2,⋯,n−k,n,n−k+1,n−1,n−k+2,⋯]
🍁代码:(Java、C++)
Java
class Solution {public int[] constructArray(int n, int k) {int[] ans = new int[n];for(int i = 1; i <= n - k; i++){//前半部分相邻差均为1ans[i - 1] = i;}int low = n - k + 1;int high = n;int i = n - k;while(low <= high){//后半部分交叉排序ans[i++] = high--;if(i >= n) break;ans[i++] = low++;}return ans;}
}
C++
class Solution {
public:vector<int> constructArray(int n, int k) {vector<int> ans(n);for(int i = 1; i <= n - k; i++){//前半部分相邻差均为1ans[i - 1] = i;}int low = n - k + 1;int high = n;int i = n - k;while(low <= high){//后半部分交叉排序ans[i++] = high--;if(i >= n) break;ans[i++] = low++;}return ans;}
};
🚀 运行结果:
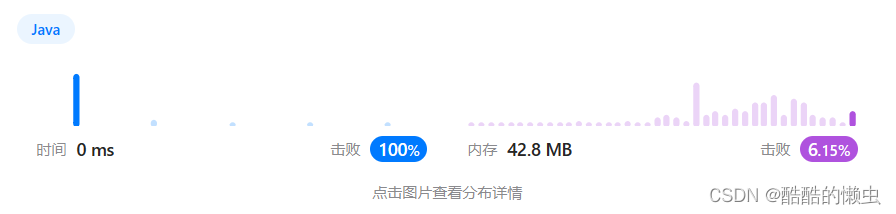
🕔 复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1),这里不计入返回值需要的空间,只需常数级空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我 leetCode专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II 难度:中等 给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件: 假设该列表是 answer [a1, a2, a3, ... , an] ࿰…...

【python基础语法七】python内置函数和内置模块
内置全局函数 abs 绝对值函数 print(abs(-1)) # 1 print(abs(100)) # 100round 四舍五入 """奇进偶不进(n.5的情况特定发生)""" res round(3.87) # 4 res round(4.51) # 5 # res round(2.5) # 2 # res round(3.5) # 4 res round(6.5) # …...

81. read readline readlines 读取文件的三种方法
81. read readline readlines 读取文件的三种方法 文章目录 81. read readline readlines 读取文件的三种方法1. 读取文件的三种方法2. read方法3. readline方法4. readlines方法5. 代码总结5.1 read方法读取全部内容5.2 readline方法读取一行,返回字符串5.3 readli…...

【社区图书馆】【图书活动第四期】
目录 一、前言 二、作者简介 三、《PyTorch高级机器学习实战》内容简介 四、书目录 一、前言 今天,偶尔逛到csdn社区图书馆,看到有活动 “【图书活动第四期】来一起写书评领实体奖牌红包电子勋章吧!”(活动到今天结束…...
)
webpack学习指南(上)
构建流程 Webpack 的构建流程可以分为以下几个步骤: 解析配置文件:Webpack 会读取项目中的 webpack.config.js 文件,并解析其中的配置项。 解析入口文件:Webpack 通过配置文件中设置的 entry 入口,递归地解析出所有依…...
刷题记录˃ʍ˂
一、1033. 移动石子直到连续 思路 这道题是一道数学题,它一共分为三种可能 第一种可能为三个石子本来就是连续的时候 第二种可能为最少步数为1的时候,相邻石子不能大于一格 第三种可能为最少步数为2的时候,这时相邻石子大于一格 那么第二…...
Word2vec原理+实战学习笔记(二)
来源:投稿 作者:阿克西 编辑:学姐 前篇:Word2vec原理实战学习笔记(一) 视频链接:https://ai.deepshare.net/detail/p_5ee62f90022ee_zFpnlHXA/6 5 对比模型(论文Model Architectur…...

什么是Java的多线程?
Java的多线程是指在同一时间内,一个程序中同时运行多个线程。每个线程都是一个独立的执行路径,可以独立地执行代码。Java中的多线程机制使得程序可以更高效地利用计算机的多核处理器和CPU时间,从而提高程序的性能和响应能力。 创建和使用Jav…...

“use strict“是什么? 使用它有什么优缺点?
严格模式 - JavaScript | MDN Javascript 严格模式详解 - 阮一峰的网络日志 1、"use strict" 是什么? "use strict" :指定代码在严格条件下执行; 2、 使用 "use strict" 有什么优缺点? ① 严格模式通过抛出错…...
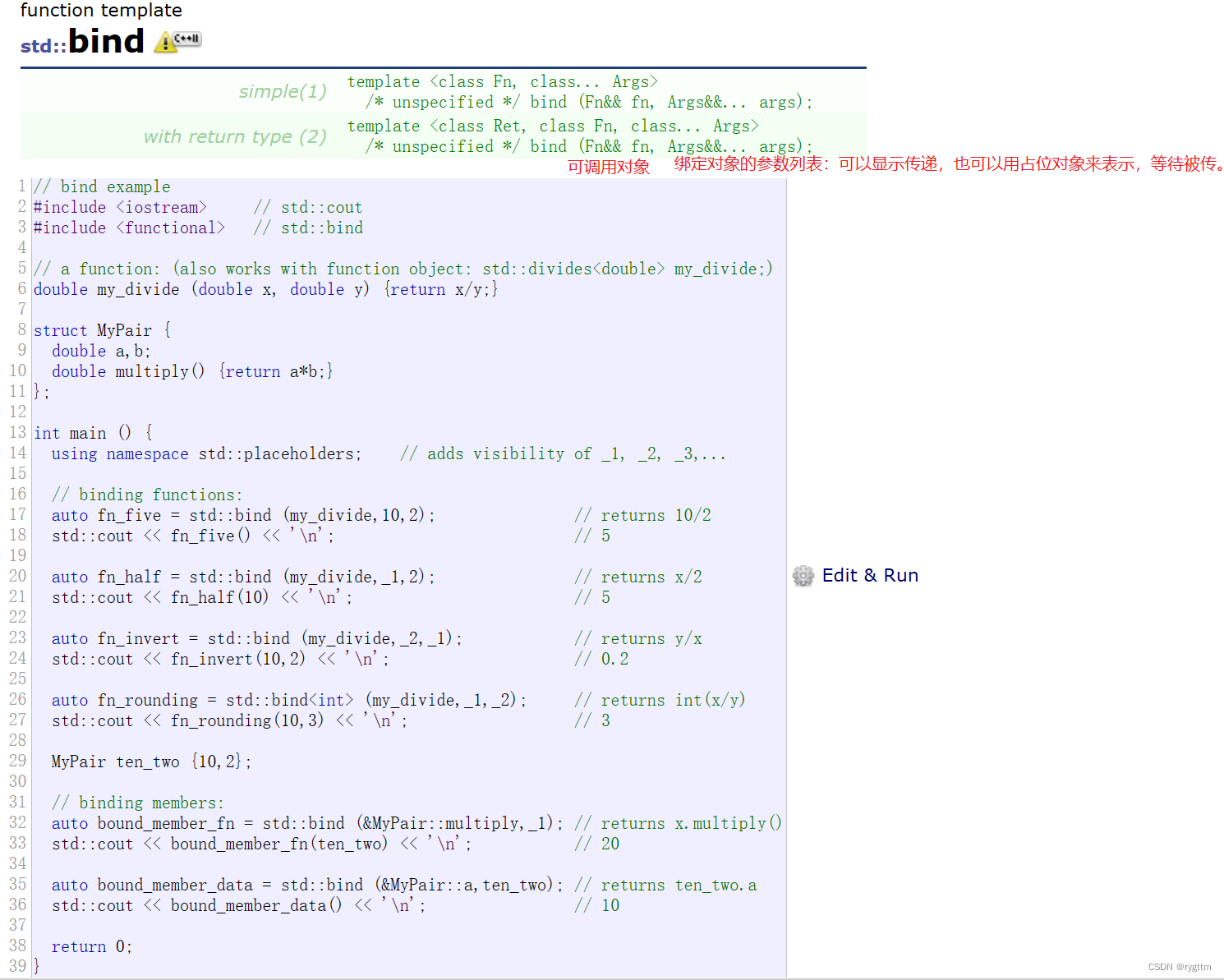
【C++】C++11常用特性总结
哥们哥们,把书读烂,困在爱里是笨蛋! 文章目录 一、统一的列表初始化1.统一的{}初始化2.std::initializer_list类型的初始化 二、简化声明的关键字1.decltype2.auto && nullptr 三、STL中的一些变化1.新增容器:array &…...

泛型——List 优于数组
数组与泛型有很大的不同: 1. 数组是协变的(covariant) 意思是:如果Sub是Super的子类型,则数组类型Sub[] 是数组类型Super[] 的子类型。 2. 泛型是不变的(invariant) 对于任何两种不同的类型Ty…...

JavaScript中对象的定义、引用和复制
JavaScript是一种广泛使用的脚本语言,其设计理念是面向对象的范式。在JavaScript中,对象就是一系列属性的集合,每个属性包含一个名称和一个值。属性的值可以是基本数据类型、对象类型或函数类型,这些类型的值相互之间有着不同的特…...

JavaScript通过函数异常处理来输入圆的半径,输出圆的面积的代码
以下为实现通过函数异常处理来输入圆的半径,输出圆的面积的代码和运行截图 目录 前言 一、通过函数异常处理来输入圆的半径,输出圆的面积 1.1 运行流程及思想 1.2 代码段 1.3 JavaScript语句代码 1.4 运行截图 前言 1.若有选择,您可以…...

Ubuntu 安装 Mysql
主要内容 本文主要是实现在虚拟机 Ubuntu 18.04 成功安装 MySQL 5.7,并实现远程访问功能,以 windows 下客户端访问虚拟机上的 mysql 数据库。 1. 切换至 root 用户 ,shell 终端指令均执行在 root 用户下 sudo su 2. 安装并设置 mysql 安…...

【五一创作】【Midjourney】Midjourney 连续性人物创作 ② ( 获取大图和 Seed 随机种子 | 通过 seed 随机种子生成类似图像 )
文章目录 一、获取大图和 Seed 随机种子二、通过 seed 种子生成类似图像 一、获取大图和 Seed 随机种子 注意 : 一定是使用 U 按钮 , 在生成的大图的基础上 , 添加 信封 表情 , 才能获取该大图的 Seed 种子编码 ; 在上一篇博客生成图像的基础上 , 点击 U3 获取第三张图的大图 ;…...
分布式事务 --- Seata事务模式、高可用
一、事务模式 1.1、XA模式 XA 规范 是 X/Open 组织定义的分布式事务处理(DTP,Distributed Transaction Processing)标准,XA 规范 描述了全局的TM与局部的RM之间的接口,几乎所有主流的数据库都对 XA 规范 提供了支持。…...

SQL(基础)
DDL: 数据定义语言 Definition,用来定义数据库对象(数据库、表、字段)CREATE、DROP、ALTER DML: 数据操作语言 Manipulation,用来对数据库表中的数据进行增删改 INSERT、UPDATE、DELETE 注意: DDL是改变表的结构 DML…...

「OceanBase 4.1 体验」OceanBase 4.1社区版的部署及使用体验
「OceanBase 4.1 体验」OceanBase 4.1社区版的部署及使用体验 一、前言1.1 本次实践介绍1.2 本次实践目的 二、准备环境资源2.1 部署前需准备工作2.2 本地环境规划 三、部署Docker环境3.1 安装Docker3.2 配置Docker镜像加速3.3 开启路由转发3.4 重启Docker服务 四、检查本地Doc…...
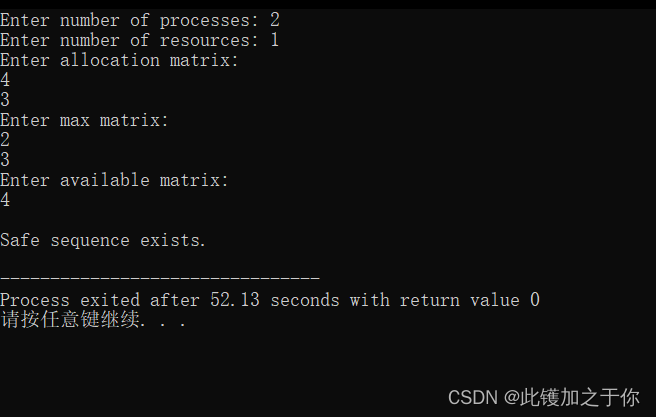
计算机操作系统实验:银行家算法模拟
目录 前言实验目的实验内容实验原理实验过程代码如下代码详解算法过程运行结果 总结 前言 本文是计算机操作系统实验的一部分,主要介绍了银行家算法的原理和实现。银行家算法是一种用于解决多个进程对多种资源的竞争和分配的算法,它可以避免死锁和资源浪…...
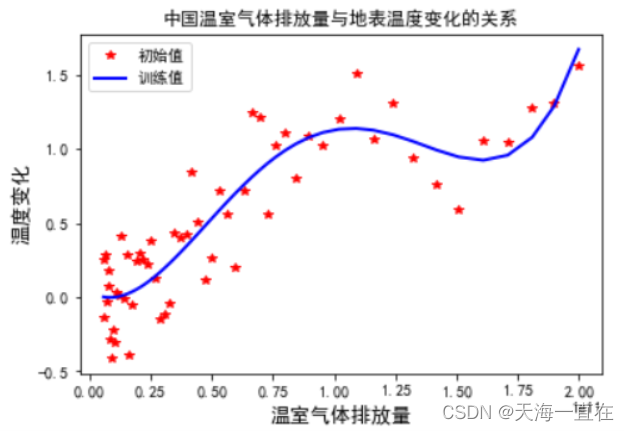
机器学习:多项式拟合分析中国温度变化与温室气体排放量的时序数据
文章目录 1、前言2、定义及公式3、案例代码1、数据解析2、绘制散点图3、多项式回归、拟合4、注意事项 1、前言 当分析数据时,如果我们找的不是直线或者超平面,而是一条曲线,那么就可以用多项式回归来分析和预测。 2、定义及公式 多项…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
