通过伴随矩阵怎么求逆矩阵
设矩阵A为n阶方阵,其伴随矩阵为Adj(A),则A的逆矩阵为:
A⁻¹ = (1/|A|) · Adj(A)
|A|为A的行列式
Adj(A)为A的伴随矩阵
具体步骤如下:
-
求出A的行列式|A|
-
求出A的伴随矩阵 Adj(A) 。伴随矩阵的定义为:对于A的第i行第j列元素,其余元素构成的(n-1)阶子阵列的行列式乘以(-1)^(i+j),即
Adj(A)ij = (-1)^(i+j) · |Aij|
其中,Aij为A中除第i行第j列元素外的其余元素构成的(n-1)阶子阵列。
- 计算A的逆矩阵A⁻¹。将Adj(A)中的每个元素除以|A|即可。
注意:如果A的行列式为0,则A没有逆矩阵。
计算例子1
给定矩阵
A =
[2 1;
4 3],求A的逆矩阵。
解:首先计算A的行列式:
|A| = 2×3 - 1×4 = 2
然后求A的伴随矩阵:
Adj(A) =
[3 -1;
-4 2]
最后计算A的逆矩阵:
A⁻¹ = (1/2) · [3 -1; -4 2] = [3/4 -1/4; -2 1]
因此,矩阵A的逆矩阵为A⁻¹ = [3/4 -1/4; -2 1]。
计算例子2
给定矩阵
B =
[1 2 3;
0 1 4;
5 6 0],
求B的逆矩阵。
解:首先计算B的行列式:
|B| = 1×(1×0-4×6) - 2×(0×0-5×6) + 3×(0×1-1×5) = -24
然后求B的伴随矩阵:
Adj(B) =
[-24 -12 18;
20 -15 -6;
-2 3 2 ]
最后计算B的逆矩阵:
B⁻¹ = (-1/24) · [-24 -12 18; 20 -15 -6; -2 3 2] = [1/4 1/4 -1/8; -5/12 -1/4 1/8; 1/8 1/12 -1/24]
因此,矩阵B的逆矩阵为B⁻¹ = [1/4 1/4 -1/8; -5/12 -1/4 1/8; 1/8 1/12 -1/24]。
相关文章:

通过伴随矩阵怎么求逆矩阵
设矩阵A为n阶方阵,其伴随矩阵为Adj(A),则A的逆矩阵为: A⁻ (1/|A|) Adj(A) |A|为A的行列式 Adj(A)为A的伴随矩阵 具体步骤如下: 求出A的行列式|A| 求出A的伴随矩阵 Adj(A) 。伴随矩阵的定义为:对于A的第i行第j列…...

巡检机器人之仪表识别系统
作者主页:爱笑的男孩。 博客简介:分享机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。 如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666foxmail.c…...
)
面试官反感的求职者(下)
上期给大家总结了面试中常见的一些问题,今天就接着上次的话题再给大家说说HR反感的求职者,希望同学们可以自省,避免踩雷。小编从如信银行考试中心了解到的有: 第一、缺乏个性者 这种考生在答题中往往表现得千篇一律,从…...
-生存曲线(LM曲线)(补充篇))
可视化绘图技巧100篇分析篇(二)-生存曲线(LM曲线)(补充篇)
目录 前言 知识储备 生存分析中的基本概念 生存分析 (survival analysis) 事件 (event)...

【100%通过率 】【华为OD机试python】钟表重合时刻【 2023 Q1考试题 A卷|100分】
华为OD机试- 题目列表 2023Q1 点这里!! 2023华为OD机试-刷题指南 点这里!! ■ 题目描述 钟表是日常生活中不可缺少的时间度量计, 其时针、分针、秒针三者的转动速度满足特定规律(见备注)。 现在输入时刻 time ,请计算出时刻 time 小时和 time+1 小时之间, 时针和分针…...

Java线程池编码示例
第1步:自定义线程实现类 Java中多线程编码时,定义线程类有两种方式: 继承Thread类实现Runnable接口(由于Java的单继承特性,一般推荐使用此方式) public class BizThread implements Runnable {private int …...

如何优化Android 4.x系统设置字体大小
android4.x系统设置字体大小导致应用布局混乱的解决方案 在前几年,Android系统的设置界面还是相对简单的,用户可以通过设置菜单进行各种系统设置,如字体大小、壁纸、铃声等。但是随着用户对系统功能的需求越来越多,Android系统也在…...
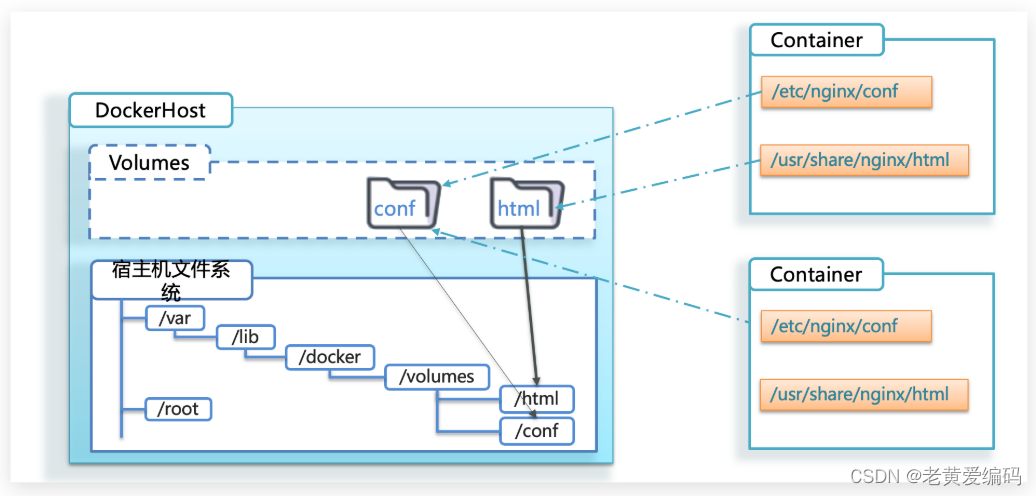
Docker安装、Docker基本操作
一、Dokcer安装 1.安装 # 1、yum 包更新到最新,需要几分钟时间(注意:也可以直接跨过) sudo yum update # 2、作用:安装需要的软件包, yum-util 提供yum-config-manager功能,另外两个是devicemapper驱动依赖的 sudo yum install -y yum-util…...

系统集成项目管理工程师知识点总结
项目经理的五种权利: 职位权力: 来源于管理者在组织中的职位和职权。罚权力: 使用降职、扣薪、惩罚、批评、威胁等负面手段的能力。奖励权力: 给予下属奖励的能力专家权力: 来源于个人的专业技能。参照(号…...

【游戏里的网络同步分析】马里奥制造2 多人模式
前置知识 先说几个游戏设计的术语。 PlayerAgent是玩家控制的网络游戏中的角色形象,也是代表在游戏空间中的玩家,被唯一PlayerController所拥有,被所有用户可观测到。 在马里奥制造2中,PlayerAgent一共有四种:马里奥 …...

SSM框架学习-注解开发第三方bean管理
1. 复习xml配置文件管理第三方bean 在Spring中,可以使用依赖注入(Dependency Injection)来管理和使用第三方Bean。Spring提供了多种方式来进行依赖注入,比如构造函数注入、Setter方法注入、字段注入等。下面以Setter方法注入为例&…...
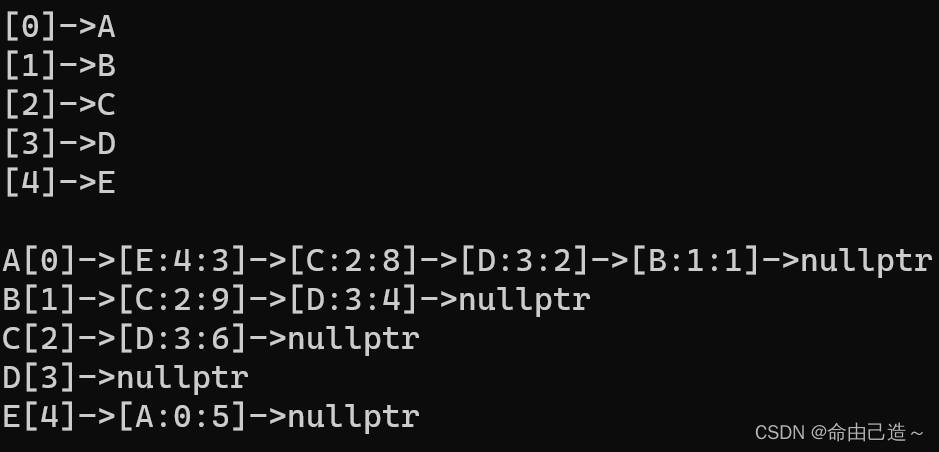
【数据结构与算法】图——邻接表与邻接矩阵
文章目录 一、图的基本概念二、图的存储结构2.1 邻接矩阵2.2 邻接表2.3 邻接矩阵的实现2.4 邻接表的实现 三、总结 一、图的基本概念 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E&#…...

网安笔记02 密码学基础
密码学概述 • 1.1、密码学的基本概念 密码编码学 : 密码编制 密码分析学 : 密码破译 密码学 : 研究密码保护 通信手段的科学, 密码编码学密码分析学 密码技术: 把可理解的消息伪装为不可理解的消息,再复原成原消息的科学 概…...

open3d io操作
目录 1. read_image, write_image 2. read_point_cloud, write_point_cloud 3. 深度相机IO操作 4. Mesh文件读取 1. read_image, write_image 读取jpg. png. bmp等文件 image_io.py import open3d as o3dif __name__ "__main__":img_data o3d.data.JuneauIma…...
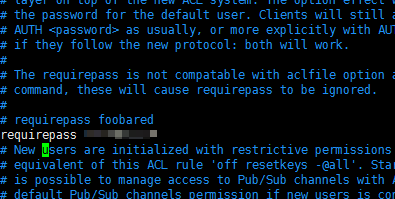
【Linux】Linux安装Redis(图文解说详细版)
文章目录 前言第一步,下载安装包第二步,上传安装包到/opt下(老规矩了,安装包在opt下)第三步,解压安装包第四步,编译第五步,安装第六步,配置redis第七步,设置开…...

setTimeout不准时,CSS精准实现计时器功能
实际开发过程中,我们会经常遇到,首次进入页面进行相应提示,然后指定时间后自动消失或者前端时钟展示等需求。 按照传统方案,我们可以使用 setTimeout 实现。但其存在:实际延时比设定值更久的情况。 setTimeout 不准时…...

单细胞跨模态分析综述
单细胞技术的最新进展使跨模态和组织位置的细胞高通量分子分析成为可能。单细胞转录组数据现在可以通过染色质可及性、表面蛋白表达、适应性免疫受体库分析和空间信息进行补充。跨模态单细胞数据的可用性越来越高,推动出新的计算方法,以帮助科学家获得生…...
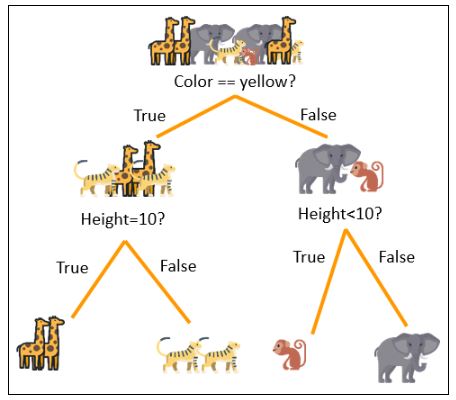
【零基础学机器学习 1】什么是机器学习?
机器学习的社会应用 1. 金融风控 机器学习在金融风控方面的应用非常广泛,可以用于预测借款人的信用风险、欺诈行为等。通过收集大量的历史数据,构建机器学习模型,可以对借款人的信用风险进行预测,从而帮助金融机构降低风险。 2…...
软开基础(一))
ARM处理器与中断——嵌入式(驱动)软开基础(一)
1 CPU的内部结构? CPU的内部结构大致可以分为: (1)控制单元(指令寄存器、指令译码器、操作控制器)。 (2)运算单元(算术逻辑单元)。 (3)存储单元(专用寄存器和通用寄存器) (4)时钟。 2 CPU跟内存、虚拟内存、硬盘的关系? (1)CPU要调用的程序和数据来自…...

WX小程序 - 2
条件渲染: wx:if "{{ newlist.length 0 }}" wx:else 跳路由:绑定点击事件,执行跳转页面 bindtap data-id"{{ item.id }}" 添加id wx.navigateTo 跳路由并传参, 下一个路由 onLoad生命周期可以获得参数…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
