【数据结构与算法】图——邻接表与邻接矩阵
文章目录
- 一、图的基本概念
- 二、图的存储结构
- 2.1 邻接矩阵
- 2.2 邻接表
- 2.3 邻接矩阵的实现
- 2.4 邻接表的实现
- 三、总结
一、图的基本概念
- 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是顶点的集合,E是边的集合。
- 在图中数据元素,我们则称之为顶点(Vertex)。
- 图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
有上面的定义可以得出树是一个特殊的图,与图的区别是没有环连通。
树关注的是节点(顶点)的值,而图关注的是顶点及边的权值。
- 图按照有无方向分为无向图和有向图。无向图由顶点和边构成,有向图由顶点和弧构成。弧有弧尾和弧头之分。
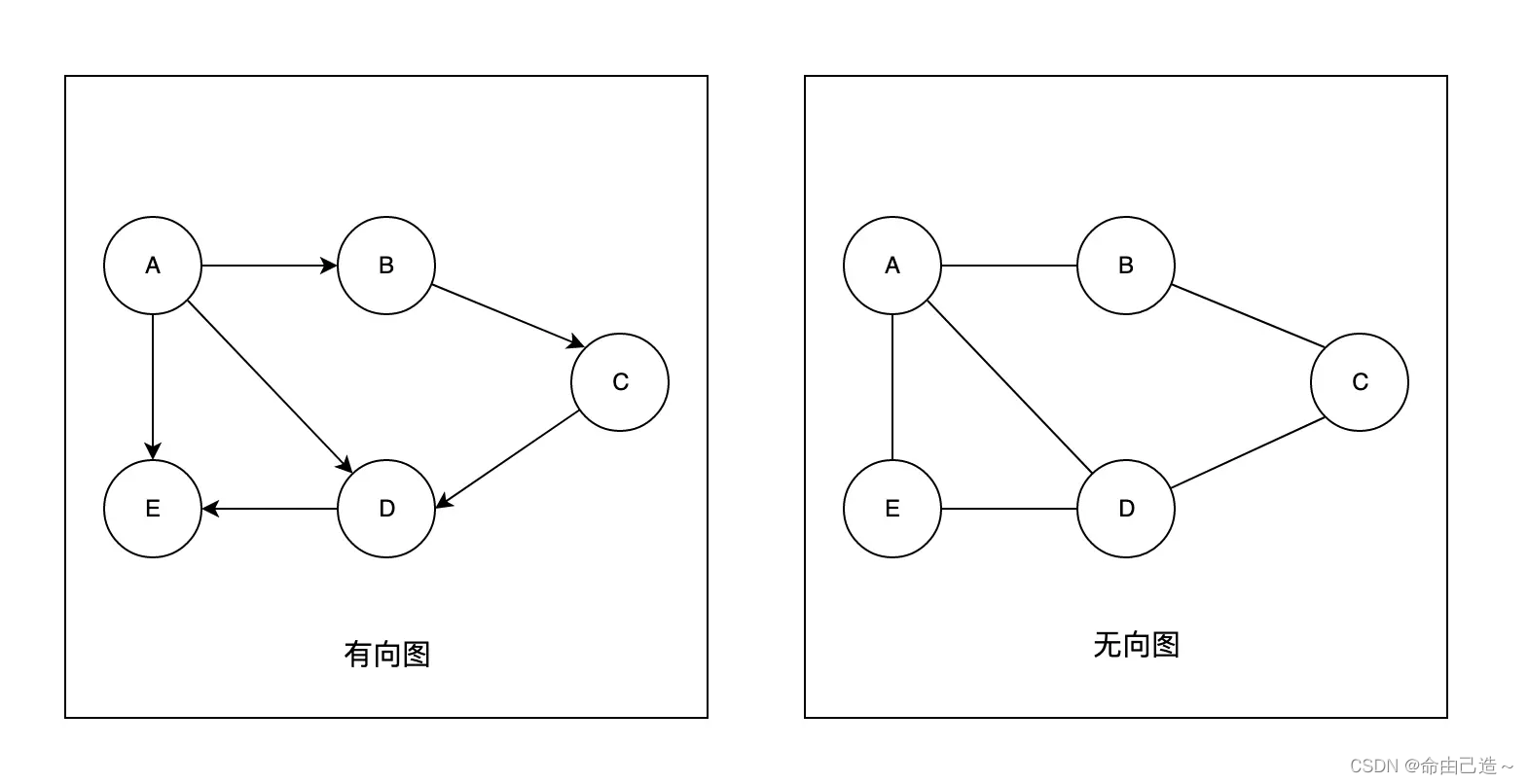
比方说现在想表示社交关系,那么QQ,微信等就是无向图,抖音微博这种就是有向图(你关注的人不一定关注了你)。
- 图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
- 图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度,有向图顶点分为入度和出度。
- 图上的边或弧上带权则称为网。
- 一个图包含了另一个图的部分顶点和部分边,就叫做子图。
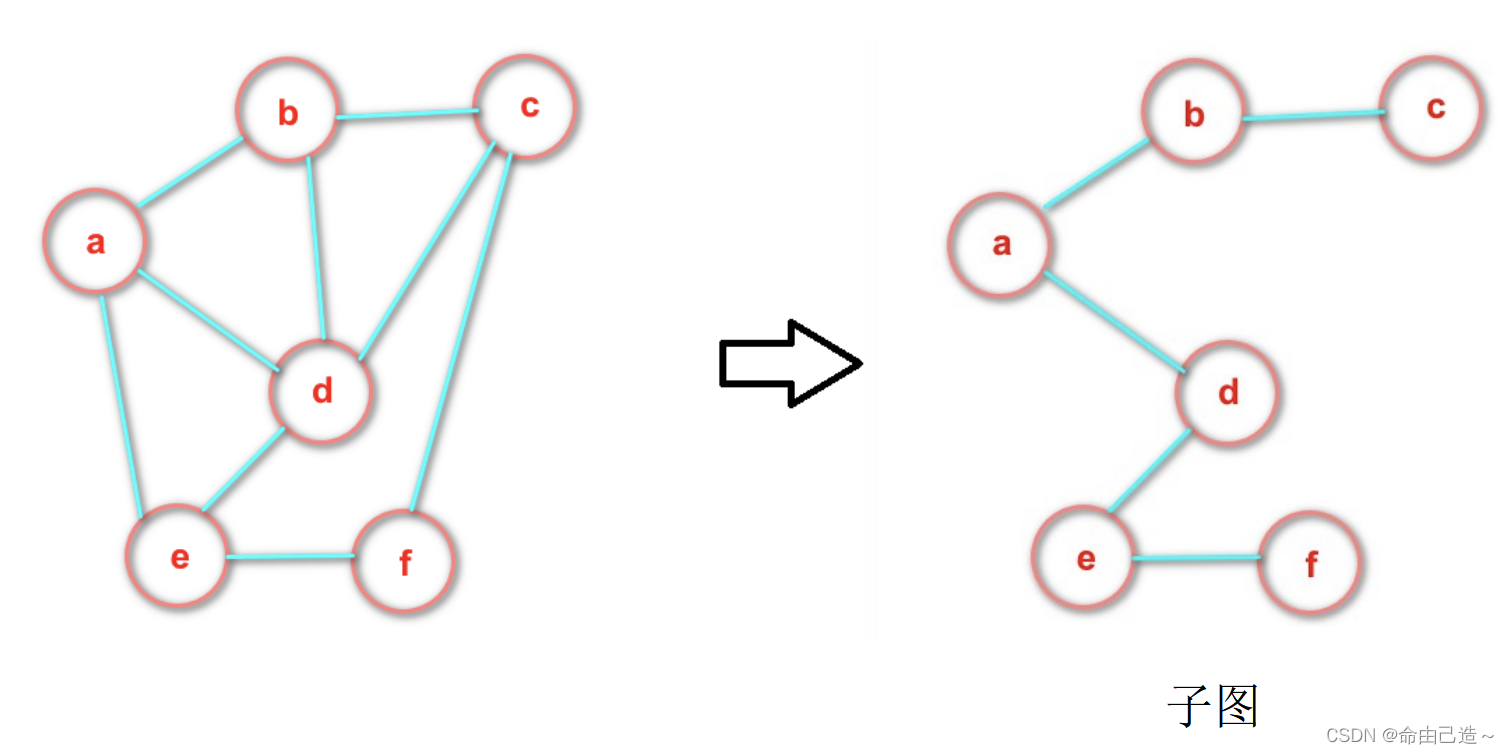
- 图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环(回路),当中不重复叫简单路径。若无向图任意两顶点都是连通的,则图就是连通图,有向则称强连通图。
- 生成树: 在无向图中,一个连通图的最小连通子图称作该图的生成树。有 n 个顶点的连通图的生成树有 n 个顶点和 n-1 条边。
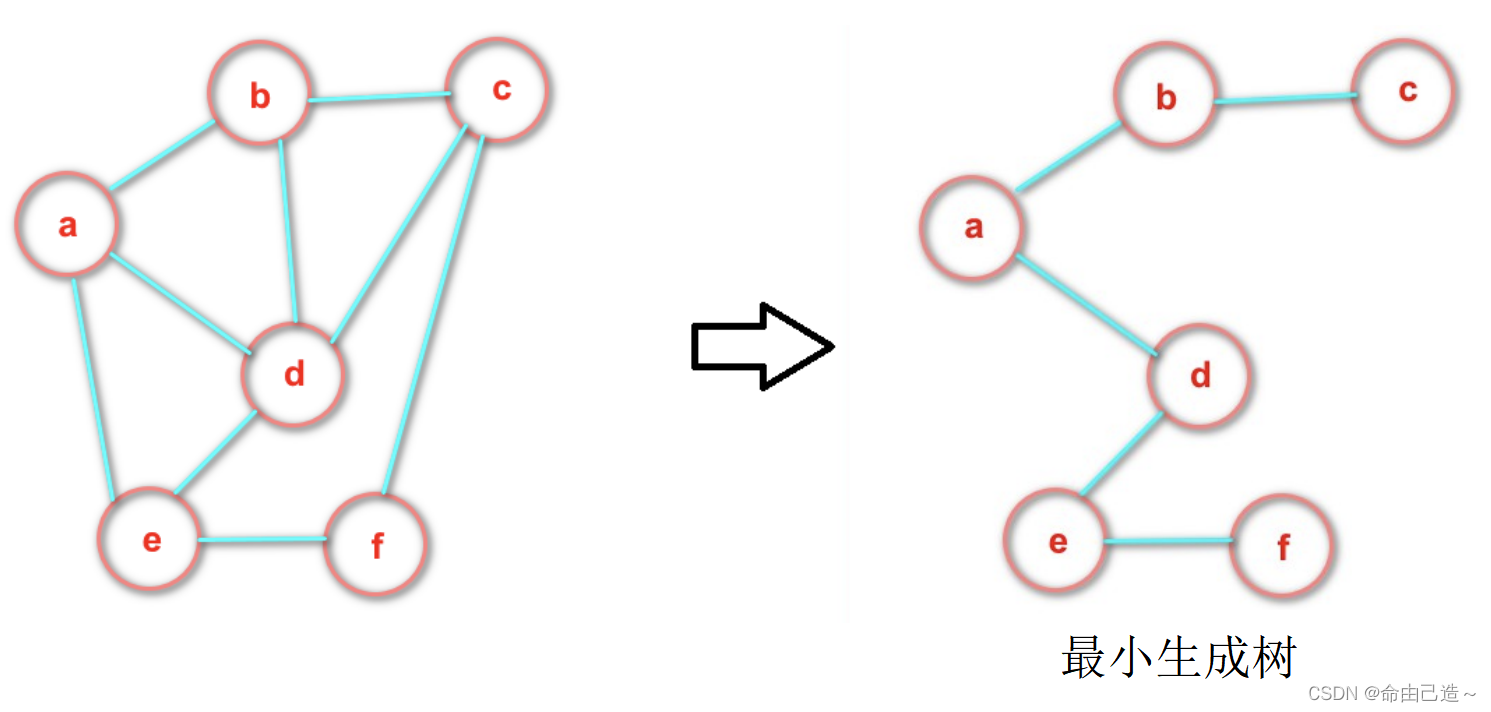
二、图的存储结构
一个图的信息包括两部分,即图中顶点的信息以及描述顶点之间的关系 ---- 边或者弧的信息。因此无论采用什么方法建立图的存储结构,都要完整、准确地反映这两个面的信息。下面介绍两种常用的图的存储结构。这篇介绍两个常见的结构:邻接矩阵和邻接表。
2.1 邻接矩阵
因为节点与节点之间的关系就是联通与否,即为 0 或者 1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。
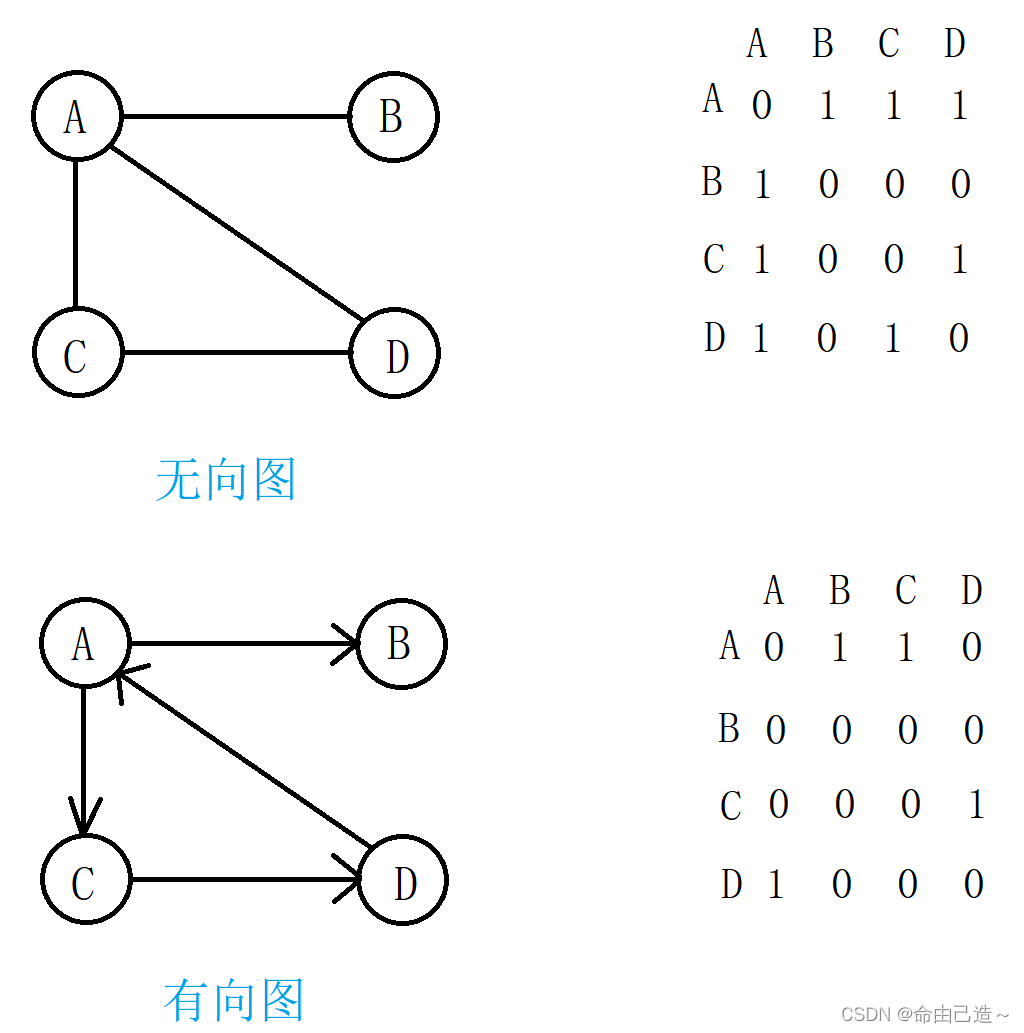
可以看出无向图是对称的,而有向图没有对称关系。
如果边是带权值的且两个顶点不相连,我们可以用INT_MAX或者INT_MIN来表示。
邻接矩阵存储图的优点是能够快速知道图中两个顶点是否连通,缺点是顶点很多且边比较少时,比较浪费空间,并且两个节点之间的路径不好求。若要确定图中有多少条边,需要遍历一遍邻接矩阵,空间复杂度为 O(N^2) 。这是用邻接矩阵来存储图的局限性。
所以邻接矩阵适合存稠密图,适合查找两个顶点是否相连
2.2 邻接表
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
用数组保存顶点,用链表保存连通的顶点。
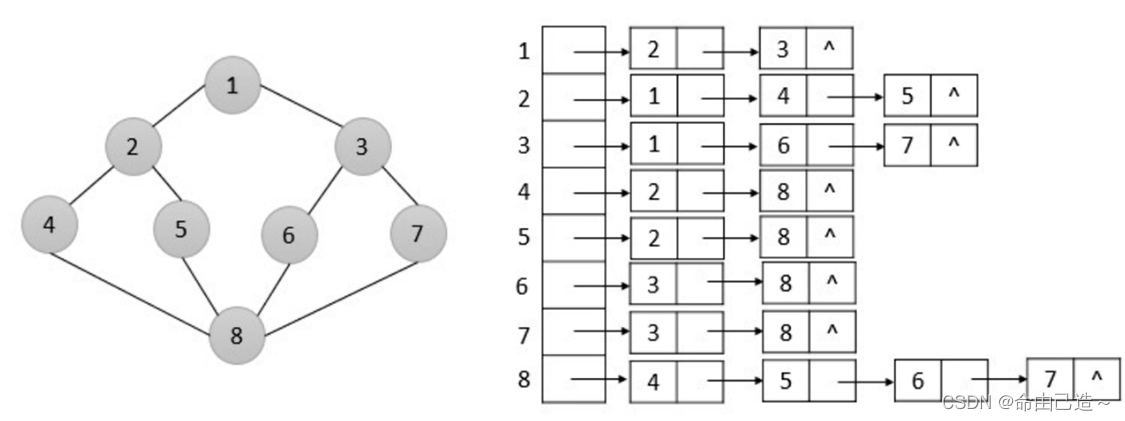
邻接表适合存稀疏图,适合查找一个顶点连出去的边
2.3 邻接矩阵的实现
邻接矩阵有以下的模板参数:
template <class V, class W, W MAX = INT_MAX, bool DIR = false>
V - 顶点,W - 权值,MAX - 最大值(默认参数给整形的最大值),DIR - 表示图是否有方向。
template <class V, class W, W MAX = INT_MAX, bool DIR = false>
class Graph
{
public:
private:vector<V> _vertexs;// 顶点集合unordered_map<V, int> _idxMap;// 顶点映射下标vector<vector<W>> _matrix;// 邻接矩阵
};
构造函数
我们传进一个数组和一个size_t型数据,数组里面存放顶点,数据表示数组的大小。
在内部我们首先要把每个顶点存储起来,并初始化邻接矩阵,把权值全部初始化成MAX代表不相连。
Graph(const V* a, size_t n)
{_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);// 将传入数组的值存储到vector中_idxMap[a[i]] = i;// 让数组中的每一个数据映射一个下标}_matrix.resize(n);for (size_t i = 0; i < n; i++){_matrix[i].resize(n, MAX);}
}
添加边
首先要获取两个顶点的下标,然后还要判断是有向图还是无向图,无向图要添加两次。
// 获取顶点下标
size_t GetIdx(const V& v)
{auto it = _idxMap.find(v);if (it == _idxMap.end()){assert(false);return -1;}return it->second;
}void addEdge(const V& src, const V& dst, const W& w)
{size_t si = GetIdx(src);size_t di = GetIdx(dst);_matrix[si][di] = w;if (DIR == false){_matrix[di][si] = w;}
}
打印观察
void Print()
{// 打印矩阵横坐标cout << " ";for (size_t i = 0; i < _vertexs.size(); ++i){printf("%5d", i);}cout << endl;// 打印矩阵for (size_t i = 0; i < _matrix.size(); ++i){cout << i << " "; // 打印矩阵纵坐标for (size_t j = 0; j < _matrix[i].size(); ++j){if (_matrix[i][j] == MAX)printf("%5c", '*');elseprintf("%5d", _matrix[i][j]);}cout << endl;}
}
整体代码
template <class V, class W, W MAX = INT_MAX, bool DIR = false>
class Graph
{
public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);// 将传入数组的值存储到vector中_idxMap[a[i]] = i;// 让数组中的每一个数据映射一个下标}_matrix.resize(n);for (size_t i = 0; i < n; i++){_matrix[i].resize(n, MAX);}}// 获取顶点下标size_t GetIdx(const V& v){auto it = _idxMap.find(v);if (it == _idxMap.end()){assert(false);return -1;}return it->second;}void addEdge(const V& src, const V& dst, const W& w){size_t si = GetIdx(src);size_t di = GetIdx(dst);_matrix[si][di] = w;if (DIR == false){_matrix[di][si] = w;}}void Print(){// 打印顶点和下标间的映射关系for (size_t i = 0; i < _vertexs.size(); ++i){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;// 打印矩阵横坐标cout << " ";for (size_t i = 0; i < _vertexs.size(); ++i){printf("%5d", i);}cout << endl;// 打印矩阵for (size_t i = 0; i < _matrix.size(); ++i){cout << i << " "; // 打印矩阵纵坐标for (size_t j = 0; j < _matrix[i].size(); ++j){if (_matrix[i][j] == MAX)printf("%5c", '*');elseprintf("%5d", _matrix[i][j]);}cout << endl;}}private:vector<V> _vertexs;// 顶点集合unordered_map<V, int> _idxMap;// 顶点映射下标vector<vector<W>> _matrix;// 邻接矩阵
};void TestGraph()
{Graph<char, int, INT_MAX, false> g("ABCDE", 5);g.addEdge('A', 'B', 1);g.addEdge('B', 'D', 4);g.addEdge('A', 'D', 2);g.addEdge('B', 'C', 9);g.addEdge('A', 'C', 8);g.addEdge('E', 'A', 5);g.addEdge('A', 'E', 3);g.addEdge('C', 'D', 6);g.Print();
}

2.4 邻接表的实现
邻接表里面存的是边,所以我们要设计一个边的类。
template <class W>
struct Edge
{Edge(int dsti, const W& w): _dsti(dsti), _w(w), _next(nullptr){}int _dsti;W _w;// 权值Edge<W>* _next;
};
当要加入一个边的时候,直接头插即可。
其他的和邻接矩阵同理。
template <class W>
struct Edge
{Edge(int dsti, const W& w): _dsti(dsti), _w(w), _next(nullptr){}int _dsti;W _w;// 权值Edge<W>* _next;
};template <class V, class W, bool DIR = false>
class Graph
{
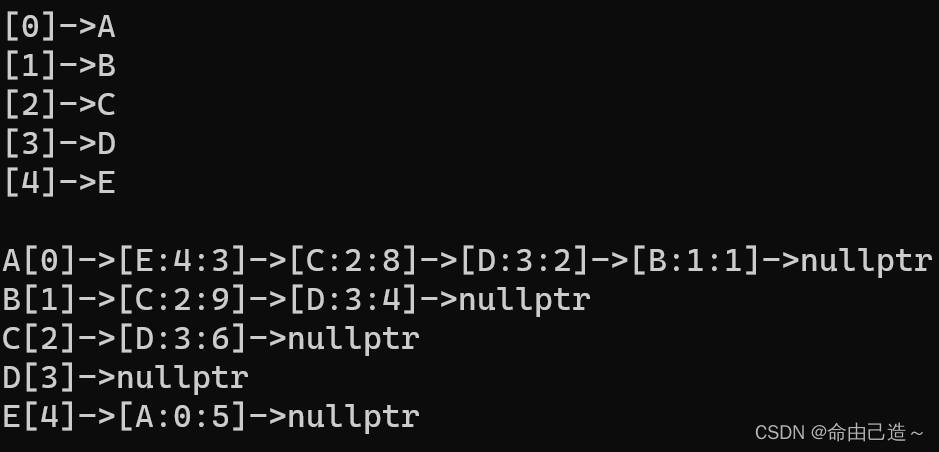
public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);// 将传入数组的值存储到vector中_idxMap[a[i]] = i;// 让数组中的每一个数据映射一个下标}_tables.resize(n, nullptr);}// 获取顶点下标size_t GetIdx(const V& v){auto it = _idxMap.find(v);if (it == _idxMap.end()){assert(false);return -1;}return it->second;}void addEdge(const V& src, const V& dst, const W& w){size_t si = GetIdx(src);size_t di = GetIdx(dst);Edge<W>* eg = new Edge<W>(di, w);eg->_next = _tables[si];_tables[si] = eg;if (DIR == false){Edge<W>* eg = new Edge<W>(si, w);eg->_next = _tables[di];_tables[di] = eg;}}void Print(){// 打印顶点和下标间的映射关系for (size_t i = 0; i < _vertexs.size(); ++i){cout << "[" << i << "]" << "->" << _vertexs[i] << endl;}cout << endl;for (size_t i = 0; i < _tables.size(); ++i){// 遍历当前链表,并打印链表结点中的相关信息cout << _vertexs[i] << "[" << i << "]->";Edge<W>* cur = _tables[i];while (cur){cout << "[" << _vertexs[cur->_dsti] << ":" << cur->_dsti << ":" << cur->_w << "]->";cur = cur->_next;}cout << "nullptr" << endl;}}private:vector<V> _vertexs;// 顶点集合unordered_map<V, int> _idxMap;// 顶点映射下标vector<Edge<W>*> _tables;// 邻接表
};void TestGraph()
{Graph<char, int, true> g("ABCDE", 5);g.addEdge('A', 'B', 1);g.addEdge('B', 'D', 4);g.addEdge('A', 'D', 2);g.addEdge('B', 'C', 9);g.addEdge('A', 'C', 8);g.addEdge('E', 'A', 5);g.addEdge('A', 'E', 3);g.addEdge('C', 'D', 6);g.Print();
}
三、总结
根据邻接表和邻接矩阵的结构特性可知,当图为稀疏图、顶点较多,即图结构比较大时,更适宜选择邻接表作为存储结构。当图为稠密图、顶点较少时,或者不需要记录图中边的权值时,使用邻接矩阵作为存储结构较为合适。
邻接表和邻接矩阵相辅相成,各有优缺点,是互补的。
相关文章:

【数据结构与算法】图——邻接表与邻接矩阵
文章目录 一、图的基本概念二、图的存储结构2.1 邻接矩阵2.2 邻接表2.3 邻接矩阵的实现2.4 邻接表的实现 三、总结 一、图的基本概念 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E&#…...

网安笔记02 密码学基础
密码学概述 • 1.1、密码学的基本概念 密码编码学 : 密码编制 密码分析学 : 密码破译 密码学 : 研究密码保护 通信手段的科学, 密码编码学密码分析学 密码技术: 把可理解的消息伪装为不可理解的消息,再复原成原消息的科学 概…...

open3d io操作
目录 1. read_image, write_image 2. read_point_cloud, write_point_cloud 3. 深度相机IO操作 4. Mesh文件读取 1. read_image, write_image 读取jpg. png. bmp等文件 image_io.py import open3d as o3dif __name__ "__main__":img_data o3d.data.JuneauIma…...
【Linux】Linux安装Redis(图文解说详细版)
文章目录 前言第一步,下载安装包第二步,上传安装包到/opt下(老规矩了,安装包在opt下)第三步,解压安装包第四步,编译第五步,安装第六步,配置redis第七步,设置开…...

setTimeout不准时,CSS精准实现计时器功能
实际开发过程中,我们会经常遇到,首次进入页面进行相应提示,然后指定时间后自动消失或者前端时钟展示等需求。 按照传统方案,我们可以使用 setTimeout 实现。但其存在:实际延时比设定值更久的情况。 setTimeout 不准时…...

单细胞跨模态分析综述
单细胞技术的最新进展使跨模态和组织位置的细胞高通量分子分析成为可能。单细胞转录组数据现在可以通过染色质可及性、表面蛋白表达、适应性免疫受体库分析和空间信息进行补充。跨模态单细胞数据的可用性越来越高,推动出新的计算方法,以帮助科学家获得生…...
【零基础学机器学习 1】什么是机器学习?
机器学习的社会应用 1. 金融风控 机器学习在金融风控方面的应用非常广泛,可以用于预测借款人的信用风险、欺诈行为等。通过收集大量的历史数据,构建机器学习模型,可以对借款人的信用风险进行预测,从而帮助金融机构降低风险。 2…...
软开基础(一))
ARM处理器与中断——嵌入式(驱动)软开基础(一)
1 CPU的内部结构? CPU的内部结构大致可以分为: (1)控制单元(指令寄存器、指令译码器、操作控制器)。 (2)运算单元(算术逻辑单元)。 (3)存储单元(专用寄存器和通用寄存器) (4)时钟。 2 CPU跟内存、虚拟内存、硬盘的关系? (1)CPU要调用的程序和数据来自…...

WX小程序 - 2
条件渲染: wx:if "{{ newlist.length 0 }}" wx:else 跳路由:绑定点击事件,执行跳转页面 bindtap data-id"{{ item.id }}" 添加id wx.navigateTo 跳路由并传参, 下一个路由 onLoad生命周期可以获得参数…...
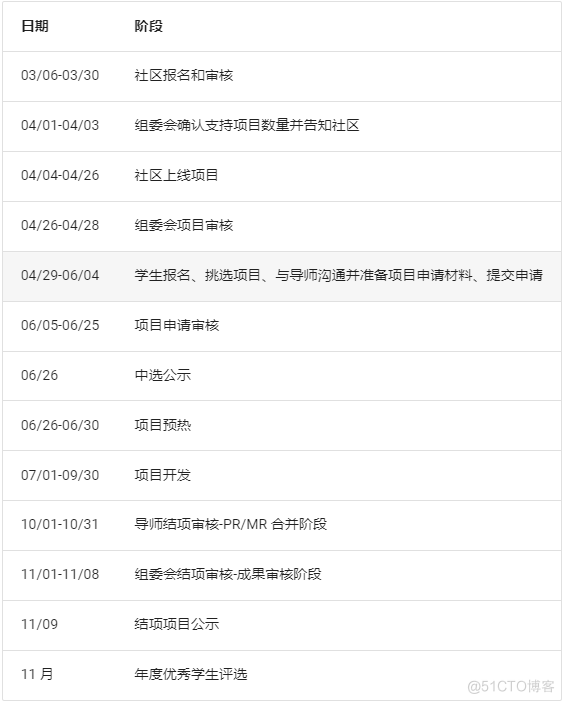
开源之夏2023 | 欢迎申请openEuler Embedded SIG开发任务
关于开源之夏 开源之夏是开源软件供应链点亮计划下的暑期活动,由中科院软件研究所与openEuler社区联合主办,旨在鼓励在校学生积极参与开源软件的开发维护,促进优秀开源软件社区的蓬勃发展。 活动联合各大开源社区,针对重要开源软件…...
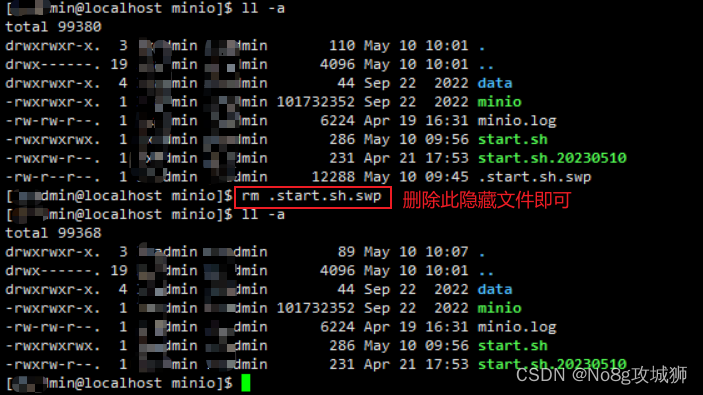
【异常解决】vim编辑文件时提示 Found a swap file by the name “.start.sh.swp“的解决方案
vim编辑文件时提示 Found a swap file by the name ".start.sh.swp"的解决方案 一、问题描述二、原因说明三、解决方案3.1 方案1 删除即可3.2 方案2 禁止生成swp文件 一、问题描述 vim编辑文件时提示 Found a swap file by the name “.start.sh.swp”,如…...

「企业应用架构」应用架构概述
在信息系统中,应用架构或应用架构是构成企业架构(EA)支柱的几个架构域之一 应用架构描述了业务中使用的应用程序的行为,重点是它们如何相互之间以及如何与用户交互。它关注的是应用程序消费和生成的数据,而不是它们的内…...
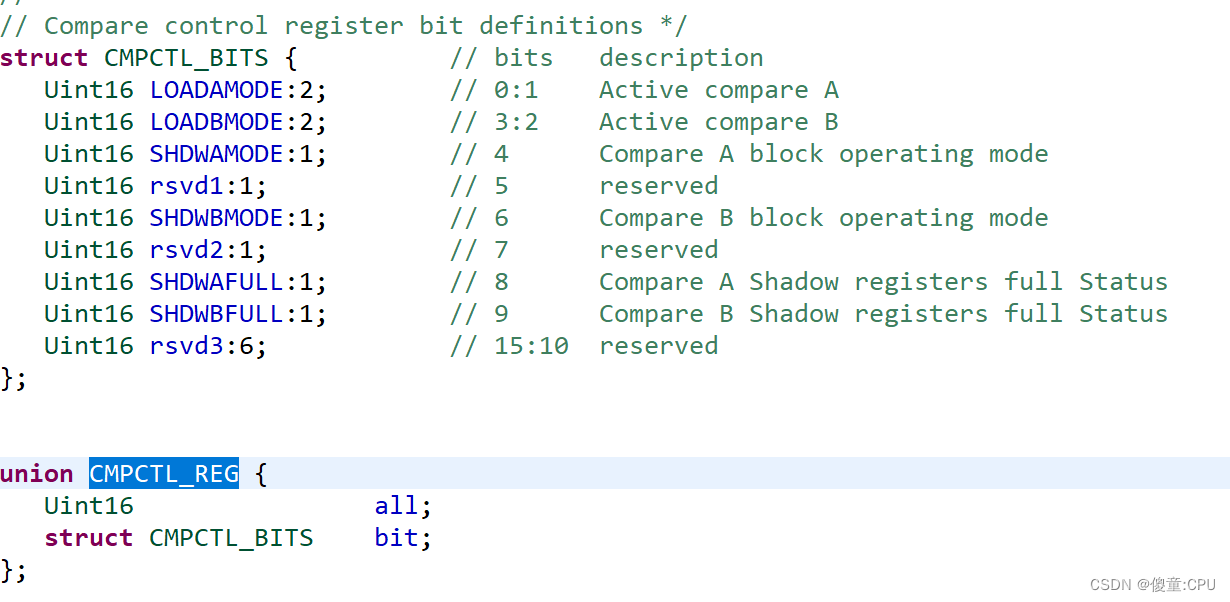
ePWM模块(3)
比较模块 CMPA:比较寄存器A,其值与TBCTR值比较,相同时,事件发送到动作模块。 CMPB:比较寄存器B,其值与TBCTR值比较,相同时,事件发送到动作模块。 CMPCTL:控制寄存器(重要) SHDWAFULL(或SHDWBFULL):CMPA(或B)阴影寄存器满标志位 0:未满 1:满了 SHDWAMODE(或…...

【笔试强训选择题】Day11.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目录…...

JVM知识
垃圾收集器就是内存回收的具体实现 Serial Serial收集器是最基本的,发展历史最悠久的收集器。在JDK1.3之前是虚拟机新生代收集的唯一选择。是一种单线程收集器,只会使用一个CPU或者一条收集线程去完成垃圾收集工作,在进行垃圾收集的时候需要…...
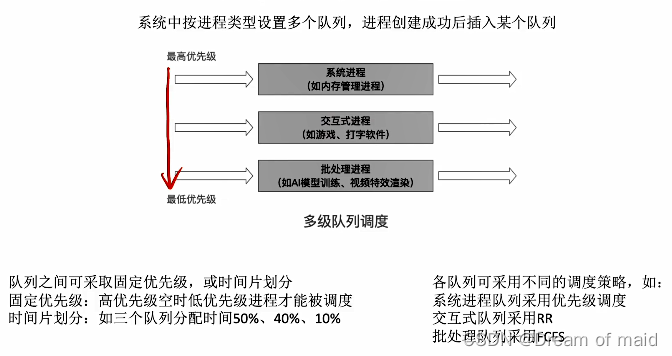
操作系统第二章——进程与线程(中)
和光同尘,与时舒卷 文章目录 2.2.1 调度的概念,层次知识总览调度的基本概念高级调度低级调度中级调度三层调度的联系,对比进程的挂起态和七状态模型知识回顾 2.2.2 进程调度的时机,切换与过程,方式知识总览进程调度的时…...

AlphaFold的极限:高中生揭示人工智能在生物信息学挑战中的缺陷
人工智能程序AlphaFold (AlphaFold2开源了,不是土豪也不会编程的你怎么蹭一波?),通过预测蛋白质结构解决了结构生物信息学的核心问题。部分AlphaFold迷们声称“该程序已经掌握了终极蛋白质物理学,其工作能力已超越了最初的设计”。…...

RocketMQ双主双从环境搭建
环境要求 64位操作系统,推荐 Linux/Unix/macOS 64位 JDK 1.8 服务器准备 准备4台服务器两台master两台slave,如果服务器紧凑,则至少需要两台服务器相互master-slave IP HOSTS 172.*******.120 rocketmq-nameserver1 rocketmq-master1 …...

next.js博客搭建_初始化next项目(第一步)
文章目录 ⭐前言⭐next初始化TypeScript 开发项目安装react的ui框架(tDesign)设计布局 ⭐结束 ⭐前言 大家好,我是yma16,本期给大家分享next项目搭建博客的开始。 背景 因为我的博客网站https://yongma16.xyz是基于vue2搭建的&am…...
ACM - 其他算法 - 基础(前缀和 + 差分)
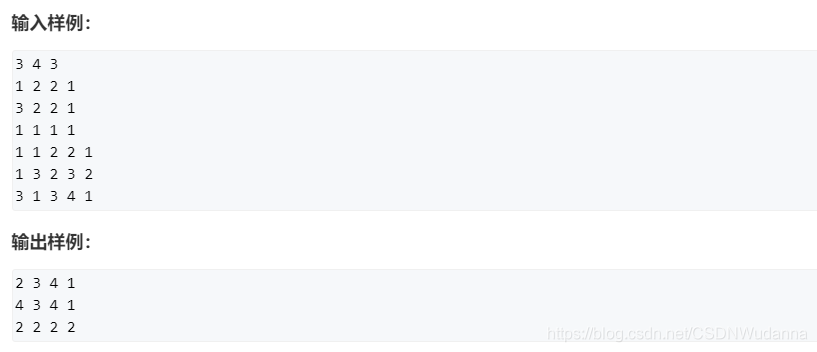
ACM- 其他算法 一、前缀和模板例题1、区间余数求K倍区间个数:AcWing 1230. K倍区间例题2、前缀和哈希求最长个数平分子串:Leetcode 面试题 17.05 字母与数字 二、差分1、一维差分2、二维差分 一、前缀和 模板 //一维前缀和 S[i] a[1] a[2] ... a[i] a[l] ... …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
