C语言printf()函数中整型格式说明符详解
每个整型在printf()函数中对应不同的格式说明符,以实现该整型的打印输出。格式说明符必须使用小写。现在让我们看看各个整型及其格式说明符:
短整型(short)
- 10进制:%hd
- 16进制:无负数格式,正数使用%hx
- 8进制:无负数格式,正数使用%ho
c
short s = 34;
printf("%hd", s); // 34
printf("%hx", s); // 22
printf("%ho", s); // 42
无符号短整型(unsigned short)
- 10进制:%hu
- 16进制:%hx
- 8进制:%ho
c
unsigned short us = 34;
printf("%hu", us); // 34
printf("%hx", us); // 22
printf("%ho", us); // 42
整型(int)
- 10进制:%i 或 %d
- 16进制:无负数格式,正数使用%x
- 8进制:无负数格式,正数使用%o
c
int i = 34;
printf("%i", i); // 34
printf("%d", i); // 34
printf("%x", i); // 22
printf("%o", i); // 42
无符号整型(unsigned int)
- 10进制:%u
- 16进制:%x
- 8进制:%o
c
unsigned int ui = 34;
printf("%u", ui); // 34
printf("%x", ui); // 22
printf("%o", ui); // 42
…
可以看出,各整型在printf()中的格式说明符虽然形式不同,但输出结果是相同的。这使我们可以方便地根据具体需要选择合适的格式说明符来实现整型的输出。
相关文章:
函数中整型格式说明符详解)
C语言printf()函数中整型格式说明符详解
每个整型在printf()函数中对应不同的格式说明符,以实现该整型的打印输出。格式说明符必须使用小写。现在让我们看看各个整型及其格式说明符: 短整型(short) 10进制:%hd16进制:无负数格式,正数使用%hx8进制:无负数格式,正数使用%ho c short s 34; printf("%hd", s…...
阿里云服务器地域和可用区怎么选择合适?
阿里云服务器地域和可用区怎么选择?地域是指云服务器所在物理数据中心的位置,地域选择就近选择,访客距离地域所在城市越近网络延迟越低,速度就越快;可用区是指同一个地域下,网络和电力相互独立的区域&#…...
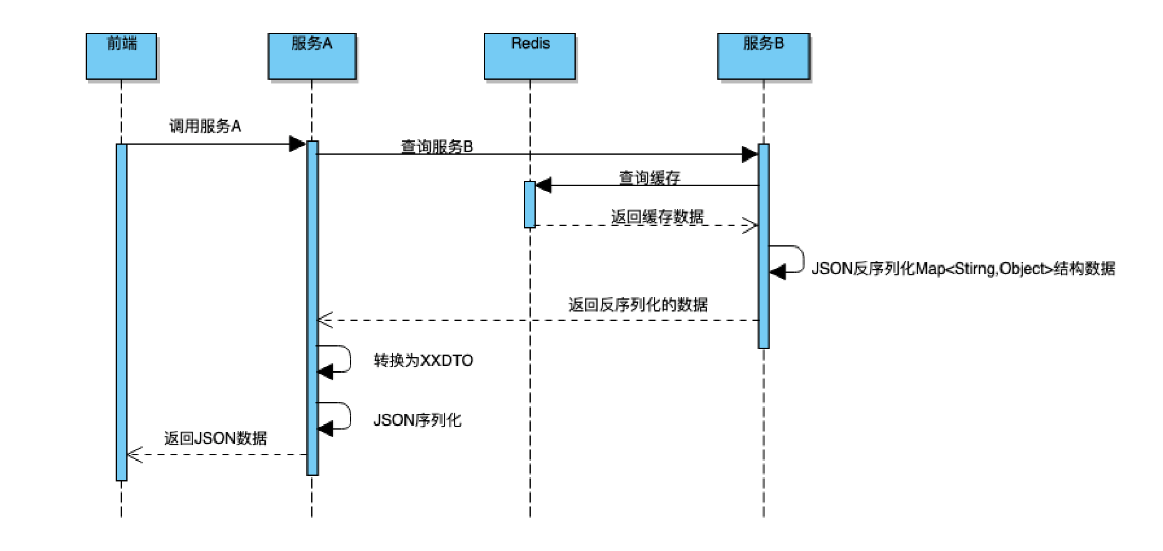
Java序列化引发的血案
1、引言 阿里巴巴Java开发手册在第一章节,编程规约中OOP规约的第15条提到: **【强制】**序列化类新增属性时,请不要修改serialVersionUID字段,避免反序列失败;如果完全不兼容升级,避免反序列化混乱&#x…...

为Linux系统添加一块新硬盘,并扩展根目录容量
我的原来ubuntu20.04系统装的时候不是LVM格式的分区, 所以先将新硬盘转成LVM,再将原来的系统dd到新硬盘,从新硬盘的分区启动,之后再将原来的分区转成LVM,在融入进来 1:将新硬盘制作成 LVM分区 我的新硬盘…...

树莓派Opencv调用摄像头(Raspberry Pi 11)
前言:本人初玩树莓派opencv,使用的是树莓派Raspberry Pi OS 11,系统若不一致请慎用,本文主要记录在树莓派上通过Opencv打开摄像头的经验。 1、系统版本 进入树莓派,打开终端输入以下代码(查看系统的版本&…...

国产ChatGPT命名图鉴
很久不见这般热闹的春天。 随着ChatGPT的威名席卷全球,大洋对岸的中国厂商也纷纷亮剑,各式本土大模型你方唱罢我登场,声势浩大的发布会排满日程表。 有趣的是,在这些大模型产品初入历史舞台之时,带给世人的第一印象其…...

操作系统——进程管理
0.关注博主有更多知识 操作系统入门知识合集 目录 0.关注博主有更多知识 4.1进程概念 4.1.1进程基本概念 思考题: 4.1.2进程状态 思考题: 4.1.3进程控制块PCB 4.2进程控制 思考题: 4.3线程 思考题: 4.4临界资源与临…...

第四十一章 Unity 输入框 (Input Field) UI
本章节我们学习输入框 (Input Field),它可以帮助我们获取用户的输入。我们点击菜单栏“GameObject”->“UI”->“Input Field”,我们调整一下它的位置,效果如下 我们在层次面板中发现,这个InputField UI元素包含两个子元素&…...

10.集合
1.泛型 1.1泛型概述 泛型的介绍 泛型是JDK5中引入的特性,它提供了编译时类型安全检测机制 泛型的好处 把运行时期的问题提前到了编译期间避免了强制类型转换 泛型的定义格式 <类型>: 指定一种类型的格式.尖括号里面可以任意书写,一般只写一个字母.例如:…...

强化学习p3-策略学习
Policy Network (策略网络) 我们无法知道策略函数 π \pi π所以要做函数近似,求一个近似的策略函数 使用策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 去近似策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s) ∑ a ∈ A π ( a ∣ s ; θ ) 1 \sum_{a\in …...

初学Verilog语言基础笔记整理(实例点灯代码分析)持续更新~
实例:点灯学习 一、Verilog语法学习 1. 参考文章 刚接触Verilog,作为一个硬件小白,只能尝试着去理解,文章未完…持续更新。 参考博客文章: Verilog语言入门学习(1)Verilog语法【Verilog】一文…...
关于 std::condition_variable
一. std::condition_variable是什么? std::condition_variable 是 C 标准库提供的一个线程同步的工具,用于实现线程间的条件变量等待和通知机制。 条件变量的发生通常与某个共享变量的状态改变相关。 在多线程编程中,条件变量通常和互斥锁…...
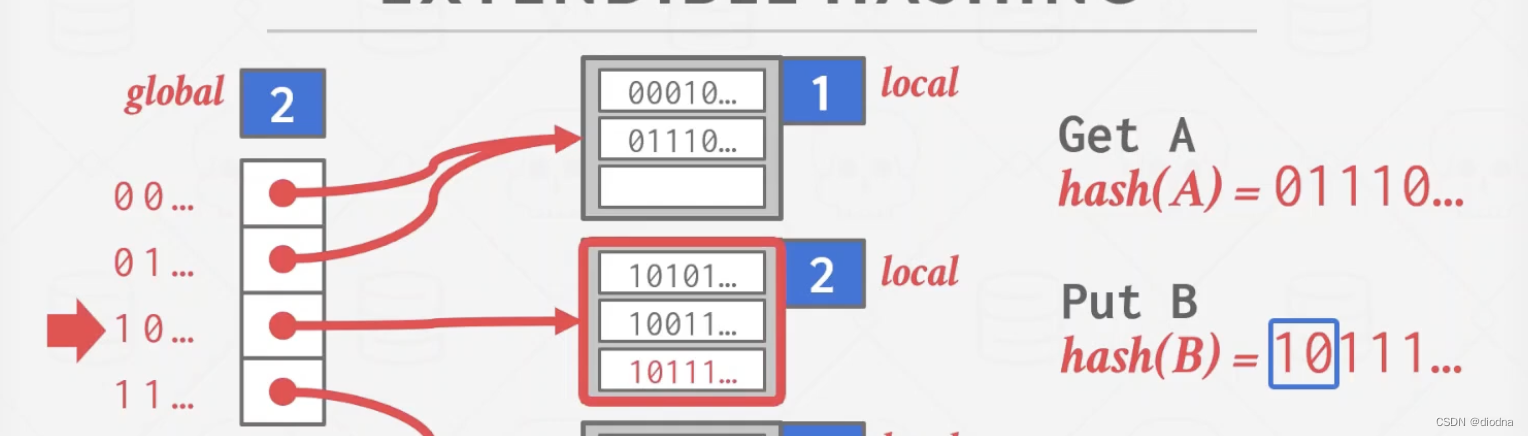
可拓展哈希
可拓展哈希 借CMU 15445的ppt截图来说明问题。 我们传统静态hash的过程是hash函数后直接将值存入对应的bucket,但是在可扩展hash中,得查询Directory(左),存入directory指向的bucket(右)。 下面…...

Java 版 spring cloud 工程系统管理 +二次开发 工程项目管理系统源码
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

通过伴随矩阵怎么求逆矩阵
设矩阵A为n阶方阵,其伴随矩阵为Adj(A),则A的逆矩阵为: A⁻ (1/|A|) Adj(A) |A|为A的行列式 Adj(A)为A的伴随矩阵 具体步骤如下: 求出A的行列式|A| 求出A的伴随矩阵 Adj(A) 。伴随矩阵的定义为:对于A的第i行第j列…...

巡检机器人之仪表识别系统
作者主页:爱笑的男孩。 博客简介:分享机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。 如发现文章有误,麻烦请指出,我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666foxmail.c…...
)
面试官反感的求职者(下)
上期给大家总结了面试中常见的一些问题,今天就接着上次的话题再给大家说说HR反感的求职者,希望同学们可以自省,避免踩雷。小编从如信银行考试中心了解到的有: 第一、缺乏个性者 这种考生在答题中往往表现得千篇一律,从…...
-生存曲线(LM曲线)(补充篇))
可视化绘图技巧100篇分析篇(二)-生存曲线(LM曲线)(补充篇)
目录 前言 知识储备 生存分析中的基本概念 生存分析 (survival analysis) 事件 (event)...

【100%通过率 】【华为OD机试python】钟表重合时刻【 2023 Q1考试题 A卷|100分】
华为OD机试- 题目列表 2023Q1 点这里!! 2023华为OD机试-刷题指南 点这里!! ■ 题目描述 钟表是日常生活中不可缺少的时间度量计, 其时针、分针、秒针三者的转动速度满足特定规律(见备注)。 现在输入时刻 time ,请计算出时刻 time 小时和 time+1 小时之间, 时针和分针…...

Java线程池编码示例
第1步:自定义线程实现类 Java中多线程编码时,定义线程类有两种方式: 继承Thread类实现Runnable接口(由于Java的单继承特性,一般推荐使用此方式) public class BizThread implements Runnable {private int …...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
