C/C++趣味程序设计百例(41~50)
C/C++语言经典、实用、趣味程序设计编程百例精解(5)
41.马克思手稿中的数学题
马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,在一家饭馆吃饭花了50先令;每个男人花3先令,每个女人花2先令,每个小孩花1先令;问男人、女人和小孩各有几人?
*问题分析与算法设计
设x,y,z分别代表男人、女人和小孩。按题目的要求,可得到下面的方程:
x+y+z=30 (1)
3x+2y+z=50 (2)
用方程程序求此不定方程的非负整数解,可先通过(2)-(1)式得:
2x+y=20 (3)
由(3)式可知,x变化范围是0~10
*程序说明与注释
#include <stdio.h>
int main() {int x, y, z, count = 0;printf(" Men Women Children\n");printf("………………………………….\n");for (x = 0; x <= 10; x++) {y = 20 - 2 * x; /*x定值据(3)式求y*/z = 30 - x - y; /*由(1)式求z*/if (3 * x + 2 * y + z == 50) /*当前得到的一组解是否满足式(2)*/printf(" %2d: %d %d %d\n", ++count, x, y, z);}
}42.最大公约数和最小公倍数
求任意两个正整数的最大公约数和(GCD)和最小公倍数(LCM)
*问题分析与算法设计
手工方式求两个正整数的蝚大公约数的方法是用辗转相除法,在程序中可以模拟这种方式。
*程序说明与注释
#include <stdio.h>
int main() {int a, b, num1, num2, temp;printf("Input a & b:");scanf("%d%d", &num1, &num2);if (num1 > num2) /*找出两个数中的较大值*/{temp = num1;num1 = num2;num2 = temp; /*交换两个整数*/}a = num1;b = num2;while (b != 0) /*采用辗转相除法求最大公约数*/{temp = a % b;a = b;b = temp;}printf("The GCD of %d and %d is: %d\n", num1, num2, a); /*输出最大公约数*/printf("The LCM of them is: %d\n", num1 * num2 / a); /*输出最小公倍数*/
}*运行结果
1.Input a & b: 20 55
The GCD of 20 and 55 is: 5
The LCM of them is: 220
2.Input a & b: 17 71
The GCD of 17 and 71 is: 1
The LCM of them is: 1207
3.Input a & b: 24 88
The GCD of 24 and 88 is: 8
The LCM of them is: 264
4.Input a & b: 35 85
The GCD of 35 and 85 is: 5
The LCM of them is: 595
*思考题
求一个最小的正整数,这个正整数被任意n(2<=n<=10)除都是除不尽的,而且余数总是(n-1)。例如:被9除时的余数为8。要求设计一个算法,不允许枚举与除2、除3、….、除9、除10有关的命令,求出这个正整数。
43.分数比较
比较两个分数的大小。
*问题分析与算法设计
人工方式下比较分数大小最常用的方法是:进行分数的通分后比较分子的大小。可以编程模拟手式方式。
*程序说明与注释
#include <stdio.h>
int zxgb(int a, int b);
int main() {int i, j, k, l, m, n;printf("Input two FENSHU:\n");scanf("%d/%d,%d/%d", &i, &j, &k, &l); /*输入两个分数*/m = zxgb(j, l) / j * i; /*求出第一个分数通分后的分子*/n = zxgb(j, l) / l * k; /*求出第二个分数通分后的分子*/if (m > n)printf("%d/%d>%d/%d\n", i, j, k, l); /*比较分子的大小*/else if (m == n)printf("%d/%d=%d/%d\n", i, j, k, l); /*输出比较的结果*/elseprintf("%d/%d<%d/%d\n", i, j, k, l);
}
int zxgb(int a, int b) {long int c;int d;if (a < b)c = a, a = b, b = c; /*若a<b,则交换两变量的值*/for (c = a * b; b != 0;) {d = b;b = a % b;a = d;}return (int)c / a;
}*运行结果
输入: 4/5,6/7 输出: 4/5<6/7
输入: 8/4,16/32 输出: 8/4>16/32
输入:16/32,4/8 输出: 16/32=4/8
44.分数之和
求这样的四个自然数p,q,r,s(p<=q<=r<=s),使得以下等式成立:
1/p+1/q+1/r+1/s=1
*问题分析与算法设计
若规定p<=q<=r<=s,将原式通分、化简并整理后得到:
2<=p<5 p<=q<7 q<r<13
采用最简单的穷举方法可以很方便的求解。
程序与程序注释:
#include <stdio.h>
int main() {int p, q, r, s, count = 0;printf("The 4 fractions which sum is equal 1 are:\n");for (p = 2; p < 5; p++) /*穷举分母*/for (q = p; q < 7; q++)for (r = q; r < 13; r++)if (p * q * r - q * r - p * r - p * q != 0) {s = (p * q * r) / (p * q * r - q * r - p * r - p * q); /*求出s的值*/if (!((p * q * r) % (p * q * r - q * r - p * r - p * q)) && s >= r)printf("[%2d] 1/%d+1/%d+1/%d+1/%d=1\n", ++count, p, q, r, s);/*输出结果*/}
}*运行结果
*思考题
将1、2、3、4、5、6、7、8、9九个数字分成以下三种分数形式之一,每个数字只能用一次,使得该分数刚好等于一个整数。
求所有满足条件的表示形式。
(参考答案:某些自然数没有这种表示形式,如:1、2、3、4、15、18等。此外整数100有11种满足条件的表示形式;89的表示形式最多,共有36种;三种形式中,最大可表示的整数为794。)
45.将真分数分解为埃及分数
分子为1 的分数称为埃及分数,现输入一个真分数,请将该分数分解为埃及分数。
如:8/11=1/2+1/5+1/55+1/110。
*问题分析与算法设计
若真分数的分子a能整除分母b,则真分数经过化简就可以得到埃及分数,若真分数的分子不能整除分母,则可以从原来的分数中分解出一个分母为b/a+1的埃及分数。用这种方法将剩余部分反复分解,最后可得到结果。
*程序说明与注释
#include <stdio.h>
int main(void) {long int a, b, c;while (true) {printf("Please enter a optional fraction(a/b):");scanf("%ld/%ld", &a, &b); /*输入分子a和分母b*/printf("It can be decomposed to:");while (true) {if (b % a) /*若分子不能整除分母*/c = b / a + 1; /*则分解出一个分母为b/a+1的埃及分数*/else {c = b / a;a = 1;} /*否则,输出化简后的真分数(埃及分数)*/if (a == 1) {printf("1/%ld\n", c);break; /*a为1标志结束*/} elseprintf("1/%ld + ", c);a = a * c - b; /*求出余数的分子*/b = b * c; /*求出余数的分母*/if (a == 3) /*若余数为3,输出最后两个埃及分数*/{printf("1/%ld + 1/%ld\n", b / 2, b);break;}}}return 0;
}*运行结果
Please enter a optional fraction (a/b): 1/6
It can be decomposed to: 1/6
Please enter a optional fraction (a/b): 20/33
It can be decomposed to: 1/2+1/10+1/165
Please enter a optional fraction (a/b): 10/89
It can be decomposed to: 1/9+1/801
Please enter a optional fraction (a/b): 19/99
It can be decomposed to: 1/6+1/40+1/3960
Please enter a optional fraction (a/b): 8/87
It can be decomposed to: 1/11+1/957
……(按ctrl-c退出)
46.列出真分数序列
按递增顺序依次列出所有分母为40,分子小于40的最简分数。
*问题分析与算法设计
对分子采用穷举法,利用最大公约数的方法,判断分子与40是否构成真分数。
*程序说明与注释
#include <stdio.h>
int main() {int i, num1, num2, temp;printf("The fraction serials with demominator 40 is:\n");for (i = 1; i <= 40; i++) /*穷举40以内的全部分子*/{num1 = 40;num2 = i;while (num2 != 0) /*采用辗转相除法求出最大公约数*/{temp = num1 % num2;num1 = num2;num2 = temp;}if (num1 == 1) /*若最大公约数为1,则为最简真分数*/printf("%d/40 ", i);}
}*运行结果
The fraction serials with demominator 40 is:
1/40 3/40 7/40 9/40 11/40 13/40 17/40 19/40
21/40 23/40 27/40 29/40 31/40 33/40 37/40 39/40
*思考题
按递增顺序依次列出所有分母小于等于40的最简真分数
47.计算分数的精确值
使用数组精确计算M/N(0<M<N<=100)的值。如果M/N是无限循环小数,则计算并输出它的第一循环节,同时要求输出 循环节的起止位置(小数位的序号)
*问题分析与算法设计
由于计算机字长的限制,常规的浮点运算都有精度限制,为了得到高精度的计算结果,就必须自行设计实现方法。
为了实现高精度的计算,可将商存放在一维数组中,数组的每个元素存放一位十进制数,即商的第一位存放在第一个元素中,商的第二位存放在第二个元素中….,依次类推。这样就可以使用数组不表示一个高精度的计算结果。
进行除法运算时可以模拟人的手工操作,即每次求出商的第一位后,将余数乘以10,再计算商的下一位,重复以上过程,当某次计算后的余数为0 时,表示M/N为有限不循环小数某次计算后的余数与前面的某个余数相同时,则M/N为无限循环小数,从该余数第一次出现之后所求得的各位数就是小数的循环节。
程序具体实现时,采用了数组和其它一些技巧来保存除法运算所得到的余数和商的各位数。
*程序说明与注释
#include <stdio.h>
int remainder[101],quotient[101]; /*remainder:存放除法的余数; quotient:依次存放商的每一位*/
int main() {int m, n, i, j;printf("Please input a fraction(m/n)(<0<m<n<=100):");scanf("%d/%d", &m, &n); /*输入被除数和除数*/printf("%d/%d it's accuracy value is:0.", m, n);for (i = 1; i <= 100; i++) /*i: 商的位数*/{remainder[m] = i; /*m:除的余数 remainder[m]:该余数对应的商的位数*/m *= 10; /*余数扩大10位*/quotient[i] = m / n; /*商*/m = m % n; /*求余数*/if (m == 0) /*余数为0 则表示是有限小数*/{for (j = 1; j <= 1; j++)printf("%d", quotient[j]); /*输出商*/break; /*退出循环*/}if (remainder[m] != 0) /*若该余数对应的位在前面已经出现过*/{for (j = 1; j <= i; j++)printf("%d", quotient[j]); /*则输出循环小数*/printf("\n\tand it is a infinite cyclic fraction from %d\n",remainder[m]);printf("\tdigit to %d digit after decimal point.\n", i);/*输出循环节的位置*/break; /*退出*/}}
}*思考题
使用数组实现计算M*N的精确值
48.新娘和新郞
三对情侣参加婚礼,三个新郞为A、B、C,三个新娘为X、Y、Z。有人不知道谁和谁结婚,于是询问了六位新人中的三位,但听到的回答是这样的:A说他将和X结婚;X说她的未婚夫是C;C说他将和Z结婚。这人听后知道他们在开玩笑,全是假话。请编程找出谁将和谁结婚。
*问题分析与算法设计
将A、B、C三人用1,2,3表示,将X和A结婚表示为“X=1”,将Y不与A结婚表示为“Y!=1”。按照题目中的叙述可以写出表达式:
x!=1 A不与X结婚
x!=3 X的未婚夫不是C
z!=3 C不与Z结婚
题意还隐含着X、Y、Z三个新娘不能结为配偶,则有:
x!=y且x!=z且y!=z
穷举以上所有可能的情况,代入上述表达式中进行推理运算,若假设的情况使上述表达式的结果均为真,则假设情况就是正确的结果。
*程序说明与注释
#include <stdio.h>
int main() {int x, y, z;for (x = 1; x <= 3; x++) /*穷举x的全部可能配偶*/for (y = 1; y <= 3; y++) /*穷举y的全部可能配偶*/for (z = 1; z <= 3; z++) /*穷举z的全部可能配偶*/if (x != 1 && x != 3 && z != 3 && x != y && x != z &&y != z) /*判断配偶是否满足题意*/{printf("X will marry to %c.\n", 'A' + x - 1); /*打印判断结果*/printf("Y will marry to %c.\n", 'A' + y - 1);printf("Z will marry to %c.\n", 'A' + z - 1);}
}*运行结果
X will marry to B. (X与B结婚)
Y will marry to C. (Y与C结婚)
Z will marry to A. (Z与A结婚)
49.委派任务
某侦察队接到一项紧急任务,要求在A、B、C、D、E、F六个队员中尽可能多地挑若干人,但有以下限制条件:
1)A和B两人中至少去一人;
2)A和D不能一起去;
3)A、E和F三人中要派两人去;
4)B和C都去或都不去;
5)C和D两人中去一个;
6)若D不去,则E也不去。
问应当让哪几个人去?
*问题分析与算法设计
用A、B、C、D、E、F六个变量表示六个人是否去执行任务的状态,变量的值为1,则表示该人去;变量的值为0,则表示该人不参加执行任务,根据题意可写出表达式:
a+b>1 A和B两人中至少去一人;
a+d!=2 A和D不能一起去;
a+e+f==2 A、E、F三人中要派两人去;
b+c==0或b+c==2 B和C都去或都不去;
c+d==1 C和D两人中去一个;
d+e==0或d==1 若D不去,则E也不去(都不去;或D去E随便)。
上述各表达式之间的关系为“与”关系。穷举每个人去或不去的各种可能情况,代入上述表达式中进行推理运算,使上述表达式均为“真”的情况就是正确的结果。
*程序说明与注释
#include <stdio.h>
int main() {int a, b, c, d, e, f;for (a = 1; a >= 0; a--) /*穷举每个人是否去的所有情况*/for (b = 1; b >= 0; b--) /*1:去 0:不去*/for (c = 1; c >= 0; c--)for (d = 1; d >= 0; d--)for (e = 1; e >= 0; e--)for (f = 1; f >= 0; f--)if (a + b >= 1 && a + d != 2 && a + e + f == 2 &&(b + c == 0 || b + c == 2) && c + d == 1 &&(d + e == 0 || d == 1)) {printf("A will%s be assigned. \n", a ? "" : "not");printf("B will%s be assigned. \n", b ? "" : "not");printf("C will%s be assigned. \n", c ? "" : "not");printf("D will%s be assigned. \n", d ? "" : "not");printf("E will%s be assigned. \n", e ? "" : "not");printf("F will%s be assigned. \n", f ? "" : "not");}
}*运行结果
A will be assigned. (去)
B will be assigned. (去)
C will be assigned. (去)
D will not be assigned. (不去)
E will not be assigned. (不去)
F will be assigned. (去)
*思考题
某参观团按以下条件限制从A、B、C、D、E五个地方中选若干参观点:
1)如去A,则必须去B;
2)D、E两地只能去一地;
3)B、C两地只能去一地;
4)C、D两地都去或都不去;
5)若去E地,A、D也必去。
问该团最多能去哪几个地方?
50.谁在说谎
张三说李四在说谎,李四说王五在说谎,王五说张三和李四都在说谎。现在问:这三人中到底谁说的是真话,谁说的是假话?
*问题分析与算法设计
分析题目,每个人都有可能说的是真话,也有可能说的是假话,这样就需要对每个人所说的话进行分别判断。假设三个人所说的话的真假用变量A、B、C表示,等于1表示该人说的是真话; 表示这个人说的是假话。由题目可以得到:
*张三说李四在说谎 张三说的是真话:a==1&&b==0
或 张三说的是假话:a==0&&b==1
*李四说王五在说谎 李四说的是真话:b==1&&c==0
或 李四说的是假话:b==0&&c==1
*王五说张三和李四都在说谎 王五说的是真话:c==1&&a+b==0
或 王五说的是假话:c==0&&a+b!=0
上述三个条件之间是“与”的关系。将表达式进行整理就可得到C语言的表达式:
(a&&!b||!a&&b)&&(b&&!c||!b&&c)&&(c&&a+b==0||!c&&a+b!=0)
穷举每个人说真话或说假话的各种可能情况,代入上述表达式中进行推理运算,使上述表达式均为“真”的情况就是正确的结果。
*程序说明与注释
#include <stdio.h>
int main() {int a, b, c;for (a = 0; a <= 1; a++)for (b = 0; b <= 1; b++)for (c = 0; c <= 1; c++)if ((a && !b || !a && b) && (b && !c || !b && c) &&(c && a + b == 0 || !c && a + b != 0)) {printf("Zhangsan told a %s.\n", a ? "truth" : "lie");printf("Lisi told a %s.\n", b ? "truch" : "lie");printf("Wangwu told a %s.\n", c ? "truch" : "lie");}
}*运行结果
Zhangsan told a lie (张三说假话)
Lisi told a truch. (李四说真话)
Wangwu told a lie. (王五说假话)
相关文章:
)
C/C++趣味程序设计百例(41~50)
C/C语言经典、实用、趣味程序设计编程百例精解(5) 41.马克思手稿中的数学题 马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,在一家饭馆吃饭花了50先令;每个男人花3先令,每个…...

论文阅读-2-DeepSMOTE Fusing Deep Learning and SMOTE for Imbalanced Data
文章目录 Abstract1. Introduction2. Learning From Imbalanced Data1. 数据级2. 算法级3. 集成方法 3. Deep Learning From Imbalanced Data基于深度神经网络的实例生成损失函数适应长尾识别 4. DeepSMOTEA. 动机B. 描述C. encoder-decoder框架D. 增强的损失函数E. 人工图像生…...
三种方法教你让模糊照片秒变高清图
现在随着数字相机和智能手机的普及,我们拍摄的照片数量越来越多,但是有些照片可能因为环境或技术等原因导致模糊不清,这时候我们就需要使用一些软件或工具来让照片变得清晰,以满足我们的需求。 下面介绍三种常用的照片变清晰的方…...
PyTorch深度学习实战 | 基于线性回归、决策树和SVM进行鸢尾花分类
鸢尾花数据集是机器学习领域非常经典的一个分类任务数据集。它的英文名称为Iris Data Set,使用sklearn库可以直接下载并导入该数据集。数据集总共包含150行数据,每一行数据由4个特征值及一个标签组成。标签为三种不同类别的鸢尾花,分别为&…...
服务端接口优化方案
一、背景 针对老项目,去年做了许多降本增效的事情,其中发现最多的就是接口耗时过长的问题,就集中搞了一次接口性能优化。本文将给小伙伴们分享一下接口优化的通用方案。 二、接口优化方案总结 1. 批处理 批量思想:批量操作数据…...

【并发基础】Happens-Before模型详解
目录 一、Happens-Before模型简介 二、组成Happens-Before模型的八种规则 2.1 程序顺序规则(as-if-serial语义) 2.2 传递性规则 2.3 volatile变量规则 2.4 监视器锁规则 2.5 start规则 2.6 Join规则 一、Happens-Before模型简介 除了显示引用vo…...

Kubernetes系列---Kubernetes 理论知识 | 初识
Kubernetes系列---Kubernetes 理论知识 | 初识 1.K8s 是什么?2.K8s 特性3.小拓展(业务升级)4.K8s 集群架构与组件①架构拓扑图:②Master 组件③Node 组件 五 K8s 核心概念六 官方提供的三种部署方式总结 1.K8s 是什么?…...

KingbaseES 原生XML系列三--XML数据查询函数
KingbaseES 原生XML系列三--XML数据查询函数(EXTRACT,EXTRACTVALUE,EXISTSNODE,XPATH,XPATH_EXISTS,XMLEXISTS) XML的简单使其易于在任何应用程序中读写数据,这使XML很快成为数据交换的一种公共语言。在不同平台下产生的信息,可以很容易加载XML数据到程序…...
【51单片机】点亮一个LED灯(看开发板原理图十分重要)
🎊专栏【51单片机】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【The Right Path】 🥰大一同学小吉,欢迎并且感谢大家指出我的问题🥰 目录 🍔基础内容 🏳…...
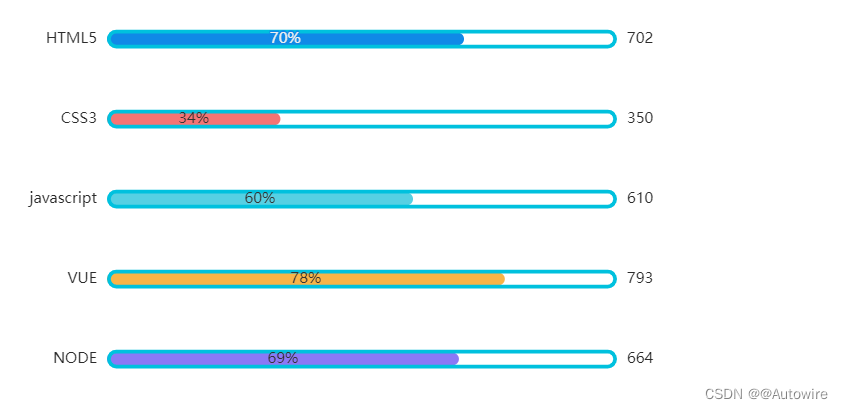
数据可视化工具 - ECharts以及柱状图的编写
1 快速上手 引入echarts 插件文件到html页面中 <head><meta charset"utf-8"/><title>ECharts</title><!-- step1 引入刚刚下载的 ECharts 文件 --><script src"./echarts.js"></script> </head>准备一个…...
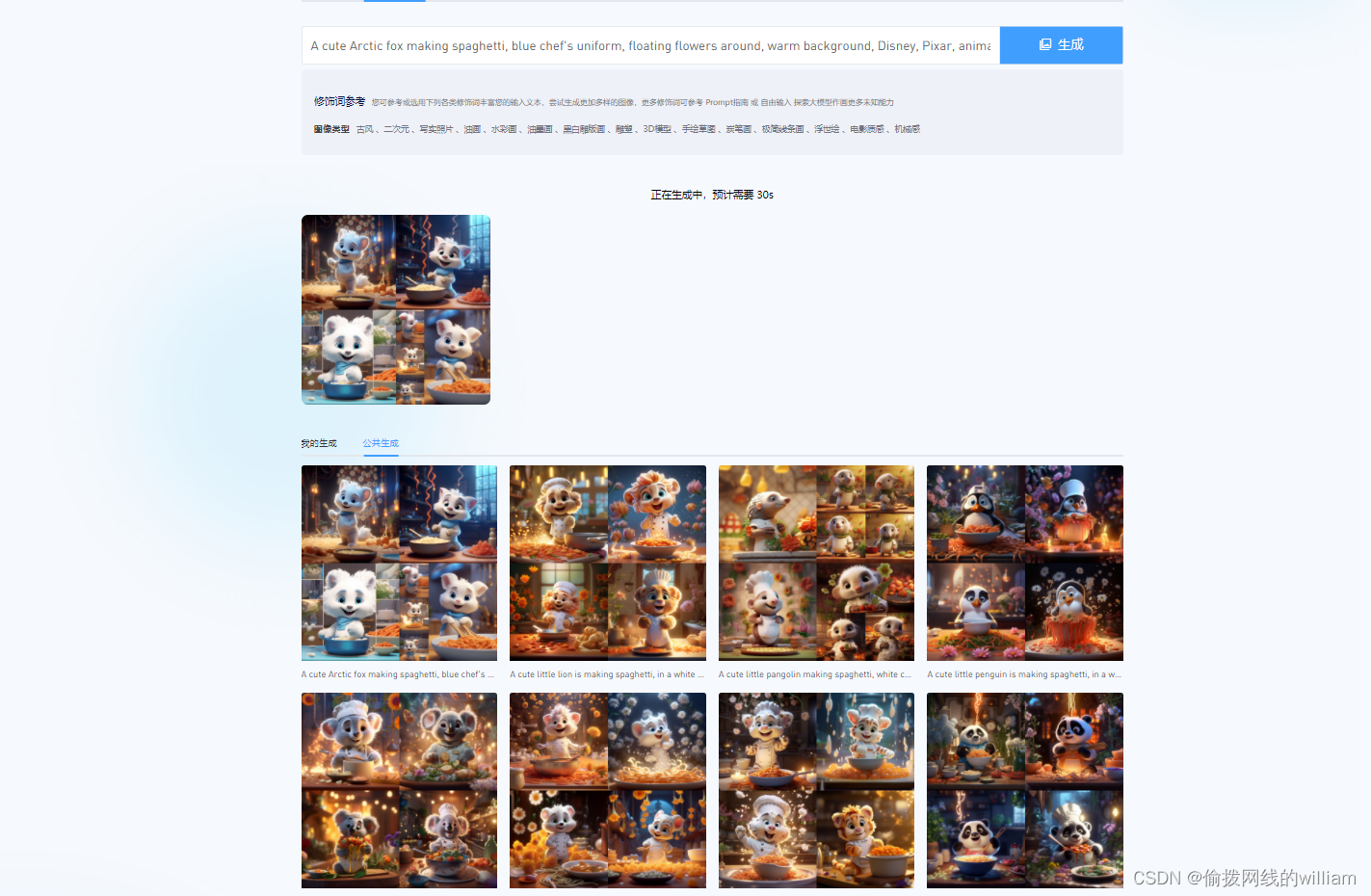
【AI绘画】——Midjourney关键词格式解析(常用参数分享)
目前在AI绘画模型中,Midjourney的效果是公认的top级别,但同时也是相对较难使用的,对小白来说比较难上手,主要就在于Mj没有webui,不能选择参数,怎么找到这些隐藏参数并且触发它是用好Mj的第一步。 今天就来…...

操作符知识点大全(简洁,全面,含使用场景,演示,代码)
目录 一.算术操作符 1.要点: 二.负数原码,反码,补码的互推 1.按位取反操作符:~(二进制位) 2.原反补互推演示 三.进制位的表示 1.不同进制位的特征: 2.二进制位表示 3.整型的二进制表…...

华工研究生语音课
这门课讲啥 语音蕴含的信息、语音识别的目的 语音的准平稳性、分帧、预加重、时域特征分析(能量和过零率)、端点检测(双门限法) 语音的基频及检测(主要是自相关法、野点的处理) 声音的产生过程…...

KingbaseES 原生XML系列二 -- XML数据操作函数
KingbaseES 原生XML系列二--XML数据操作函数(DELETEXML,APPENDCHILDXML,INSERTCHILDXML,INSERTCHILDXMLAFTER,INSERTCHILDXMLBEFORE,INSERTXMLAFTER,INSERTXMLBEFORE,UPDATEXML) XML的简单使其易于在任何应用程序中读写数据,这使XML很快成为数据交换的一种公共语言。…...
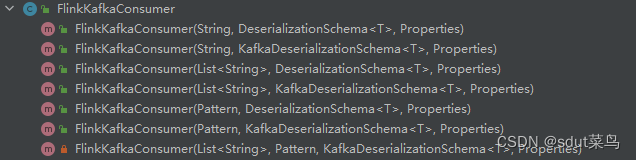
【Flink】DataStream API使用之源算子(Source)
源算子 创建环境之后,就可以构建数据的业务处理逻辑了,Flink可以从各种来源获取数据,然后构建DataStream进项转换。一般将数据的输入来源称为数据源(data source),而读取数据的算子就叫做源算子(…...
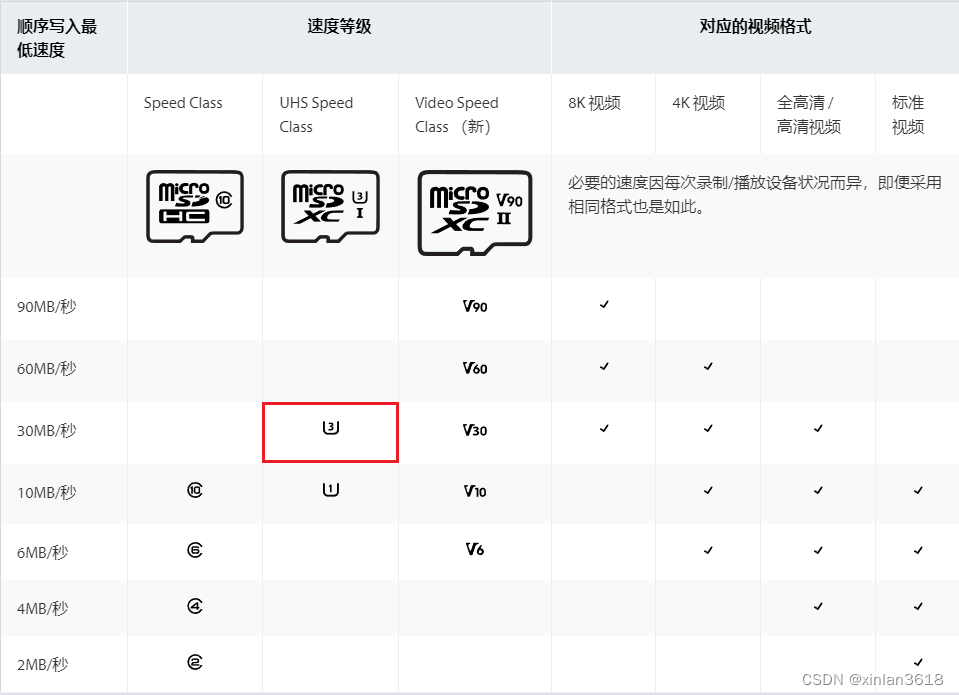
树莓派硬件介绍及配件选择
目录 树莓派Datasheet下载地址: Raspberry 4B 外观图: 技术规格书: 性能介绍: 树莓派配件选用 电源的选用: 树莓派外壳选用: 内存卡/U盘选用 树莓派Datasheet下载地址: Raspberry Pi …...
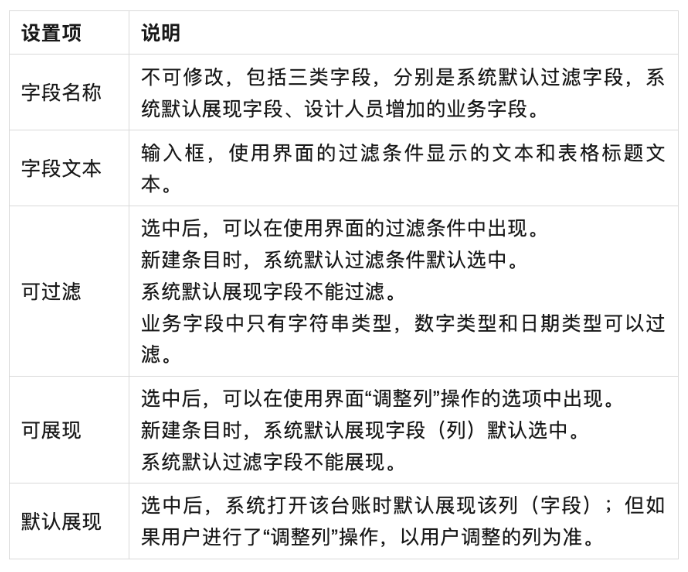
O2OA (翱途) 平台 V8.0 发布新增数据台账能力
亲爱的小伙伴们,O2OA (翱途) 平台开发团队经过几个月的持续努力,实现功能的新增、优化以及问题的修复。2023 年度 V8.0 版本已正式发布。欢迎大家到 O2OA 的官网上下载进行体验,也希望大家在藕粉社区里多提宝贵建议。本篇我们先为大家介绍应用…...

数控解锁怎么解 数控系统解锁解密
Amazon Fargate 在中国区正式落地,因 数控解锁使用 Serverless 架构,更加适合对性能要求不敏感的服务使用,Pyroscope 是一款基于 Golang 开发的应用程序性能分析工具,Pyroscope 的服务端为无状态服务且性能要求不敏感,…...
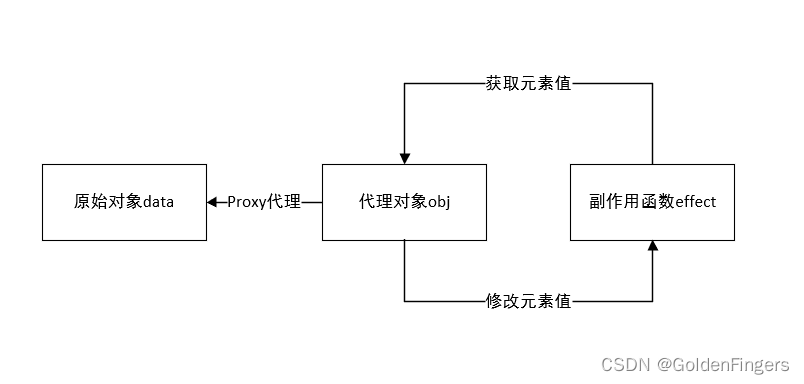
3.0 响应式系统的设计与实现
1、Proxy代理对象 Proxy用于对一个普通对象代理,实现对象的拦截和自定义,如拦截其赋值、枚举、函数调用等。里面包含了很多组捕获器(trap),在代理对象执行相应的操作时捕获,然后在内部实现自定义。 const…...
Rust 快速入门60分① 看完这篇就能写代码了
Rust 一门赋予每个人构建可靠且高效软件能力的语言https://hannyang.blog.csdn.net/article/details/130467813?spm1001.2014.3001.5502关于Rust安装等内容请参考上文链接,写完上文就在考虑写点关于Rust的入门文章,本专辑将直接从Rust基础入门内容开始讲…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
