数据结构刷题(三十一):1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II
一、1049. 最后一块石头的重量 II
1.思路:01背包问题,其中dp[j]表示容量为j的背包,最多可以背最大重量为dp[j]。
2.注意:递推公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);本题中的重量就是价值,所以第二个stone[i]表示价值的意思; 遍历顺序上仍然是先物品后背包
3.本题与分割等和子集类似,不同就在于最后return时,本题得到的target = sum / 2 因为是向下取整,所以sum - dp[target] 一定是大于等于dp[target]。
所以相撞也就是将target与sum - dp[target]作差即可。
class Solution {public int lastStoneWeightII(int[] stones) {if (stones.length == 0 || stones == null)return 0;int sum = 0;// 先求出这堆石头的和,以便得到背包能背的最大重量for (int stone : stones) {sum += stone;}int target = sum >> 1;int[] dp = new int[target + 1];// for循环, 先物品再背包for (int i = 0; i < stones.length; i++) {// 这里的内循环一定是j >= stone[i] ,否则无法判断第二个max条件for (int j = target; j >= stones[i]; j--){dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}二、完全背包
1.有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
2.核心代码:区别于01背包的一维滚动数组,差别就是内循环
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}3.计算过程

3.518. 零钱兑换 II
1.思路:完全背包。
2.递推公式:dp[j] += dp[j - nums[i]],表示填满j(包括j)这么大容积的包,有dp[j]种方法。
例如:dp[j],j 为5,
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
3.注意:该题纯完全背包是能凑成总和就行,不用管怎么凑的,不需要管顺序。
4.代码:
class Solution {public int change(int amount, int[] coins) {// dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法int[] dp = new int[amount+1];//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;for (int i = 0; i < coins.length; i++) { // 零钱的种类数for (int j = coins[i]; j <= amount; j++){ // 组合方法dp[j] += dp[j - coins[i]];}}return dp[amount];}
}相关文章:

数据结构刷题(三十一):1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II
一、1049. 最后一块石头的重量 II 1.思路:01背包问题,其中dp[j]表示容量为j的背包,最多可以背最大重量为dp[j]。 2.注意:递推公式dp[j] max(dp[j], dp[j - stones[i]] stones[i]);本题中的重量就是价值,所以第二个…...

opencv_c++学习(四)
图像在opencv中的存储方式 在上图中可以看出,在opencv中采用的是像素值来代表每一个像素三通道颜色的深浅。 Mat对象 Mat对象是在OpenCV2.0之后引进的图像数据结构、自动分配内存、不存在内存泄漏的问题,是面向对象的数据结构。分了两个部分࿰…...

基于AT89C51单片机的篮球计时记分设计
点击链接获取Keil源码与Project Backups仿真图: https://download.csdn.net/download/qq_64505944/87771065 源码获取 主要内容: 基于51单片机设计篮球计时计分器,结合单片机串行接口原理,用AT89C51设计一个篮球比赛计分计时器,能够通过数码管显示分数和比赛时间(并设有…...

并发编程-Day2
并发编程 1.共享模型-内存 共享变量在多线程间的<可见性>问题与多条指令执行时的<有序性>问题 1.1Java内存模型 JMM它定义了主存、工作内存抽象概念,底层对应着CPU寄存器、缓存、硬件内存CPU指令优化等. JMM体现在: 原子性-保证指令不会受到线程上…...

第1章 Nginx简介
基于 Nginx版本 1.14.2 ,Tomcat版本 9.0.0 演示 第1章 Nginx简介 1.1 Nginx发展介绍 Nginx (engine x) 是一个高性能的Web服务器和反向代理服务器,也可以作为邮件代理服务器。 Nginx 特点是占有内存少,并发处理能力…...
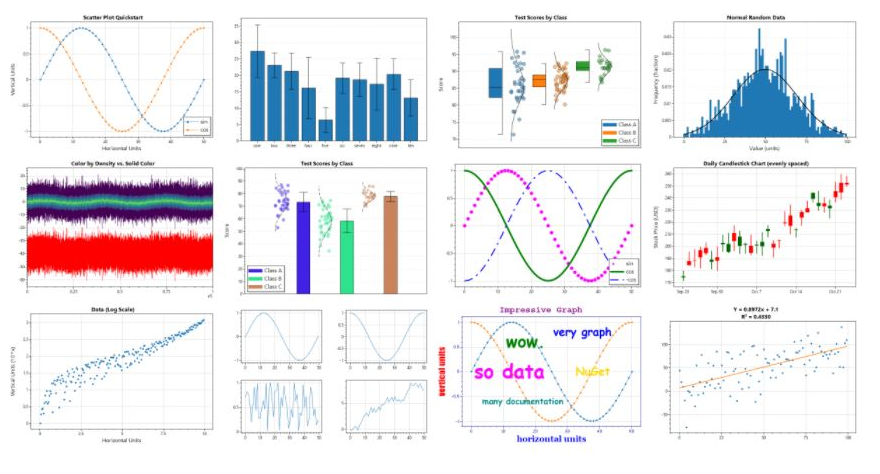
一个.Net功能强大、易于使用、跨平台开源可视化图表
可视化图表运用是非常广泛的,比如BI系统、报表统计等。但是针对桌面应用的应用,很多报表都是收费的,今天给大家推荐一个免费.Net可视化开源的项目! 项目简介 基于C#开发的功能强大、易于使用、跨平台高质量的可视化图表库&#…...

浅谈 ext2 文件系统的特点、优缺点以及使用场景
ext2(Extended File System 2)是 Linux 中最早的一种文件系统,它是 Linux 文件系统的基础,也被广泛用于其他类 Unix 系统中。下面是 ext2 文件系统的特点、优缺点以及使用场景: 特点: ext2 文件系统可以支…...

Map和Set数据结构和ES6模块化语法
Map和Set数据结构 ●ES6 新增的两种数据结构 ●共同的特点: 不接受重复数据 Set数据结构 ●是一个 类似于 数组的数据结构 ●按照索引排列的数据结构 创建 Set 数据结构 语法: var s new Set([ 数据1, 数据2, 数据3, ... ]) Set 数据结构的属性和方法 ●size 属性 ○语法: 数…...

10_Uboot启动流程_2
目录 _main函数详解 board_init_f函数详解 relocate_code函数详解 relocate_vectors函数详解 board_init_r 函数详解 _main函数详解 在上一章得知会执行_main函数_main函数定义在文件arch/arm/lib/crt0.S 中,函数内容如下: 第76行,设置sp指针为CONFIG_SYS_INIT_SP_ADDR,也…...
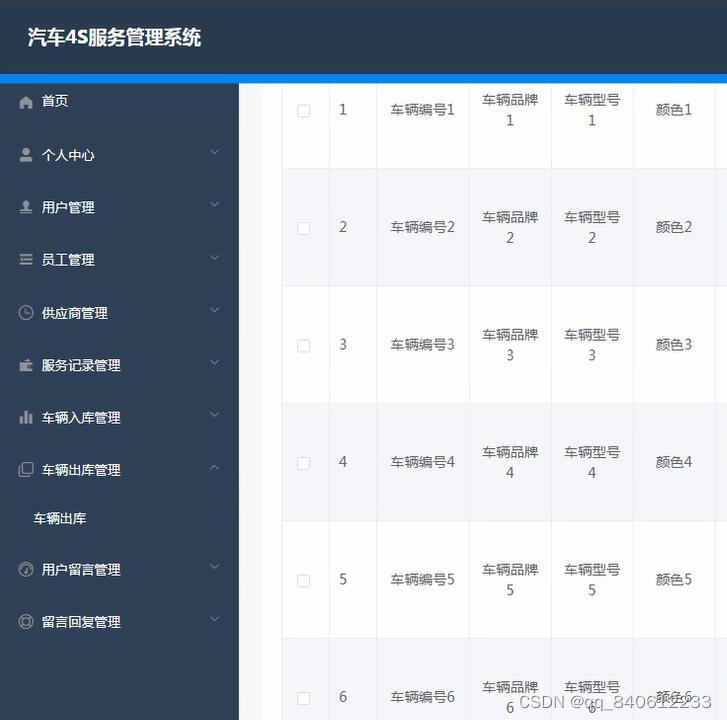
python+django汽车4S店零配件保养服务管理系统
汽车4S服务管理系统包括三种用户。管理员、普通员工、客户。 开发语言:Python 框架:django/flask Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat 开发软件:PyCharm django 应用目录结构管…...

STM32F4的输出比较极性和PWM1,PWM2的关系
PWM 输出比较通道 在这里以通用定时器的通道1作为介绍。 如图,左边就是CNT计数器和CCR1第一路的捕获/比较寄存器,它俩进行比较,当CNT>CCR1, 或者CNTCCR1时,就会给输出模式控制器传送一个信号,然后输出模式控制器就…...

易优cms伪静态,EyouCms去除URL中的index.php
针对不同服务器、虚拟空间,运行PHP的环境也有所不同,目前主要分为:Nginx、apache、IIS以及其他服务器。下面分享如何去掉URL上的index.php字符,记得在管理后台清除缓存,对于一些ECS服务器可能要重启nginx等服务! 【Nginx服务器】 在原有的nginx重写文件里新增以下代码片…...
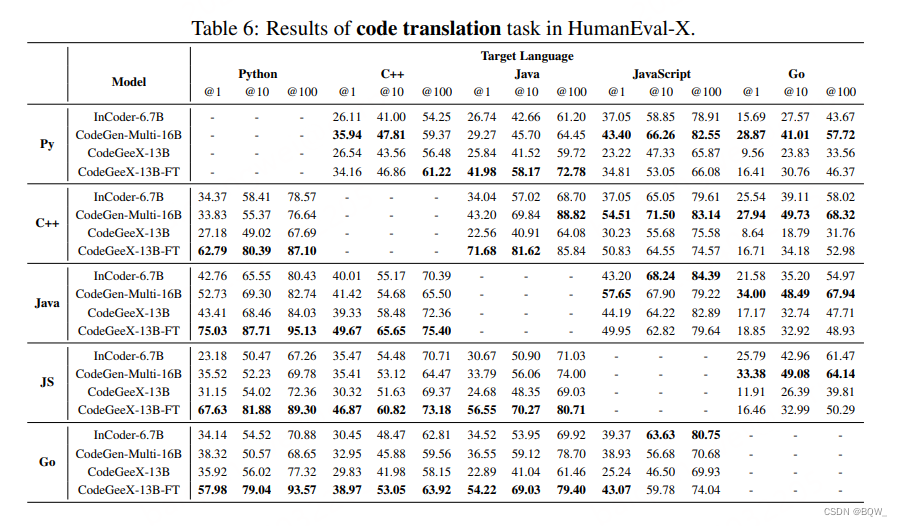
【自然语言处理】【大模型】CodeGeeX:用于代码生成的多语言预训练模型
CodeGeeX:用于代码生成的多语言预训练模型 《CodeGeeX: A Pre-Trained Model for Code Generation with Multilingual Evaluations on HumanEval-X》 论文地址:https://arxiv.org/pdf/2303.17568.pdf 相关博客 【自然语言处理】【大模型】CodeGen&#x…...

Open3D 非线性最小二乘拟合二维多项式曲线
目录 一、算法原理二、代码实现三、结果展示一、算法原理 多项式曲线表示为: p ( x ) = p 1 x n + p 2 x n...

kafka消息队列的两种模式
第一种模式: 点对点模式(一对一,消费者主动拉取数据,消息收到后消息清除) 1.消息生产者生产消息发送给队列,然后消费者从队列中取出并且消费消息 2.消息被消费以后,queue中不再有存储࿰…...
python语法复习
print:输出函数 print(520)效果:输出520. print(hello)效果:输出hello. print(1020)【效果:输出了:1020】注:“ ”在print里面是一个连接符。 print(1020)【效果:输出了30】注: 在此处…...
02-Java基础编程
Java基础编程 Java 基础语法Java 标识符变量变量的类型Java 基本数据类型基本数据类型转换 运算符常见运算符运算符的优先级 程序流程控制分支语句循环结构常用的循环结构循环的嵌套break 和 continue 关键字 数组一维数组多维数组的使用Arrays 工具类的使用数组中常见的异常 J…...
)
武忠祥老师每日一题||定积分基础训练(十)
已知f(x)连续 ∫ 0 x t f ( x − t ) d t 1 − cos x , 求 ∫ 0 π 2 f ( x ) d x 的值。 \int_{0}^{x}tf(x-t)\,{\rm d}t1-\cos x,求\int_{0}^{\frac{\pi}{2}}f(x)dx的值。 ∫0xtf(x−t)dt1−cosx,求∫02πf(x)dx的值。 已知一个关于f的变上限积分等式,&…...
)
C/C++趣味程序设计百例(41~50)
C/C语言经典、实用、趣味程序设计编程百例精解(5) 41.马克思手稿中的数学题 马克思手稿中有一道趣味数学问题:有30个人,其中有男人、女人和小孩,在一家饭馆吃饭花了50先令;每个男人花3先令,每个…...

论文阅读-2-DeepSMOTE Fusing Deep Learning and SMOTE for Imbalanced Data
文章目录 Abstract1. Introduction2. Learning From Imbalanced Data1. 数据级2. 算法级3. 集成方法 3. Deep Learning From Imbalanced Data基于深度神经网络的实例生成损失函数适应长尾识别 4. DeepSMOTEA. 动机B. 描述C. encoder-decoder框架D. 增强的损失函数E. 人工图像生…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
