代码随想录算法训练营第二十二天|235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点
目录
235. 二叉搜索树的最近公共祖先
1、递归实现
2、迭代法实现
701.二叉搜索树中的插入操作(递归实现)
450.删除二叉搜索树中的节点(递归实现)
235. 二叉搜索树的最近公共祖先
相对于 二叉树的最近公共祖先 本题就简单一些了,因为 可以利用二叉搜索树的特性。
题目链接/文章讲解:代码随想录
题解思路:
1、递归实现
迭代法和递归法实现的原理一致,其实我觉得这种迭代法本质就是递归的方法,只不过步骤不一样而已!!!
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {while(root != null){if(root.val > p.val && root.val > q.val){TreeNode left = lowestCommonAncestor(root.left,p,q);if(left != null) return left;}else if(root.val < p.val && root.val < q.val){TreeNode right = lowestCommonAncestor(root.right,p,q);if(right != null) return right;}else{return root;}}return null;}
}2、迭代法实现
迭代法和递归法实现的原理一致,其实我觉得这种迭代法本质就是递归的方法,只不过步骤不一样而已!!!
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {while(root != null){if(root.val > p.val && root.val > q.val){TreeNode left = lowestCommonAncestor(root.left,p,q);if(left != null) return left;}else if(root.val < p.val && root.val < q.val){TreeNode right = lowestCommonAncestor(root.right,p,q);if(right != null) return right;}else{return root;}}return null;}
}701.二叉搜索树中的插入操作(递归实现)
本题比想象中的简单,大家可以先自己想一想应该怎么做,然后看视频讲解,就发现 本题为什么比较简单了。
题目链接/文章讲解:代码随想录
题解思路:
多听卡哥视频讲解!!!在二叉树中插入操作就是构造二叉树,一定能在叶子节点找到我们要插入的节点,然后可以根据二叉搜索树的特性比较当前节点的val值和给定的val,直接判断在其左子树还是右子树进行插入操作!!!最后直接返回root节点就好!!!没听卡哥讲解之前,单纯一团糊浆,第一感觉很复杂,又是各种插入方式等等!!!听完卡哥视频讲解完思路还是清晰的,一刷一定要多听,多看,多刷,把思路打开!!!非科班转码确实有点痛苦,真的就颠覆之前没有训练后的思考方法!!!加油吧!!!
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {//第二步:确定终止条件if(root == null) return new TreeNode(val);;//第三步:确定单层处理逻辑if(root.val > val){root.left = insertIntoBST(root.left,val); //直接根据二叉搜索树的特性比较当前节点的val值和给定的val,直接判断在其左子树还是右子树进行插入操作}else if(root.val < val){root.right = insertIntoBST(root.right,val); //直接根据二叉搜索树的特性比较当前节点的val值和给定的val,直接判断在其左子树还是右子树进行插入操作}return root;}}作者:vansven-h
链接:https://leetcode.cn/problems/insert-into-a-binary-search-tree/solution/701er-cha-sou-suo-shu-zhong-de-cha-ru-ca-fj39/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。450.删除二叉搜索树中的节点(递归实现)
相对于 插入操作,本题就有难度了,涉及到改树的结构
题目链接/文章讲解:代码随想录
题解思路:
主要是删除节点的情况存在五种不同情况,需要根据不同情况进行一一处理,具体的5种情况见下方注释代码!!!我想说的是一刷还是要多看、多听卡哥视频、多刷,把方法论掌握的融汇贯通才有资本自己去造轮子,这些都是基础算法,都没掌握怎么去谈更进阶的知识呢!!!
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode root, int key) {//第二步:确定终止条件,当找到五种不同情况的节点需要删除时,此时就是遍历到的节点就是终止条件,需要及时对找到的节点进行处理才行if(root == null) return null; //第一种情况:没找到要删除的节点,直接返回null值即可else if(root.val == key){ //以下四种情况都是在找到要删除节点的情况下进行讨论的if(root.left == null && root.right == null) return null; //第二种情况:删除的时叶子节点else if(root.left != null && root.right == null) return root.left; //第三种情况:删除左不为空,右为空的节点else if(root.left == null && root.right != null) return root.right;//第四种情况:删除左为空,右不为空的节点else{TreeNode current = root.right; //第五种情况:删除左不为空,右不为空的节点,根据二叉搜索树的特性,需要一直搜索右子树的左节点,一直其叶节点进行插入while( current.left != null){current = current.left;}current.left = root.left;return root.right;}}//第三步:确定单层处理逻辑,根据二叉树的搜索特性,直接比较当前遍历节点的val值和key值,直接判断在其左子树还是右子树进行删除节点操作if(root.val > key) root.left = deleteNode(root.left,key);else if(root.val < key) root.right = deleteNode(root.right,key);return root;}
}相关文章:

代码随想录算法训练营第二十二天|235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点
目录 235. 二叉搜索树的最近公共祖先 1、递归实现 2、迭代法实现 701.二叉搜索树中的插入操作(递归实现) 450.删除二叉搜索树中的节点(递归实现) 235. 二叉搜索树的最近公共祖先 相对于 二叉树的最近公共祖先 本题就简单一些了…...

hbase表出现RIT删除方案
1.删除zookeeper中对应表注册信息 cd /opt/cloudera/parcels/CDH/lib/zookeeper/bin ./zkCli.sh -server node2:2181 --node2为仿真节点,生产需改 deleteall /hbase/table/表名 2.删除hdfs对应表数据 hadoop dfs -rm -r /hbase/data/default/表名 3.删除hbase:met…...
)
SQL学习(3)
SELECT 语句用于从表中选取数据。 SELECT 列名称 FROM 表名称 SELECT * FROM 表名称关键词 DISTINCT 用于返回唯一不同的值 SELECT DISTINCT 列名称 FROM 表名称WHERE 子句用于规定选择的标准 如需有条件地从表中选取数据,可将 WHERE 子句添加到 SELECT 语句。 S…...

连接型CRM助力医疗企业把“成本中心”变成“利润中心”
在市场竞争日益加剧的情形下,企业获客成本大幅上涨,存量客户的维护和开发开始被重视,售后服务部门的职责在企业中发挥的价值越来越大。因为企业售后服务不仅能帮助客户解决问题的部门,还是客户与企业沟通的桥梁,将客户…...

《Vue.js 设计与实现》—— 03 Vue.js 3 的设计思路
1. 声明式地描述 UI Vue.js 3 是一个声明式的 UI 框架,即用户在使用 Vue.js 3 开发页面时是声明式地描述 UI 的。 编写前端页面涉及的内容如下: DOM 元素:例如是 div 标签还是 a 标签属性:如 a 标签的 href 属性,再…...

2023年湖北省建设厅特种作业操作证报名条件是什么?
建筑施工特种作业人员是指在房屋建筑和市政工程施工活动中,从事可能对本人、他人及周围设备设施的安全造成重大危害作业的人员。建筑施工特种作业人员必须经建设主管部门考核合格,取得建筑施工特种作业人员操作资格证书(以下简称“资格证书”…...

Redis 进阶
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

伙伴匹配系统笔记---02
Java 8特性 1. stream / parallelStream 流失处理 2. Optional 可选类 一. 前端整合路由 1. 路由:vue 路由组件库地址:安装 | Vue Router (vuejs.org) 安装:yarn add vue-router@4 2. 整合路由: // 1. 定义路由组件. // 也可以从其他文件导入 const Home = { templ…...

Redis学习——单机版安装
目录 1.解压 2.安装gcc 3.执行make命令 4.复制redis的配置文件到默认安装目录下 5.修改redis.conf文件 6.启动redis服务与客户端 7.查看redis进行是否启动 8.关闭redis服务 9.redis性能测试 注意:安装redis前要安装jdk。 1.解压 [rootlxm148 install]# t…...

第三十一章 React中路由组件和一般组件
在React中,组件是应用程序的构建块。它们是可重用的,可以用于创建复杂的UI。React中有两种类型的组件:路由组件和一般组件。 一般组件 一般组件是React应用程序的基本构建块。它们是可重用的,可以用于创建复杂的UI。它们不知道U…...
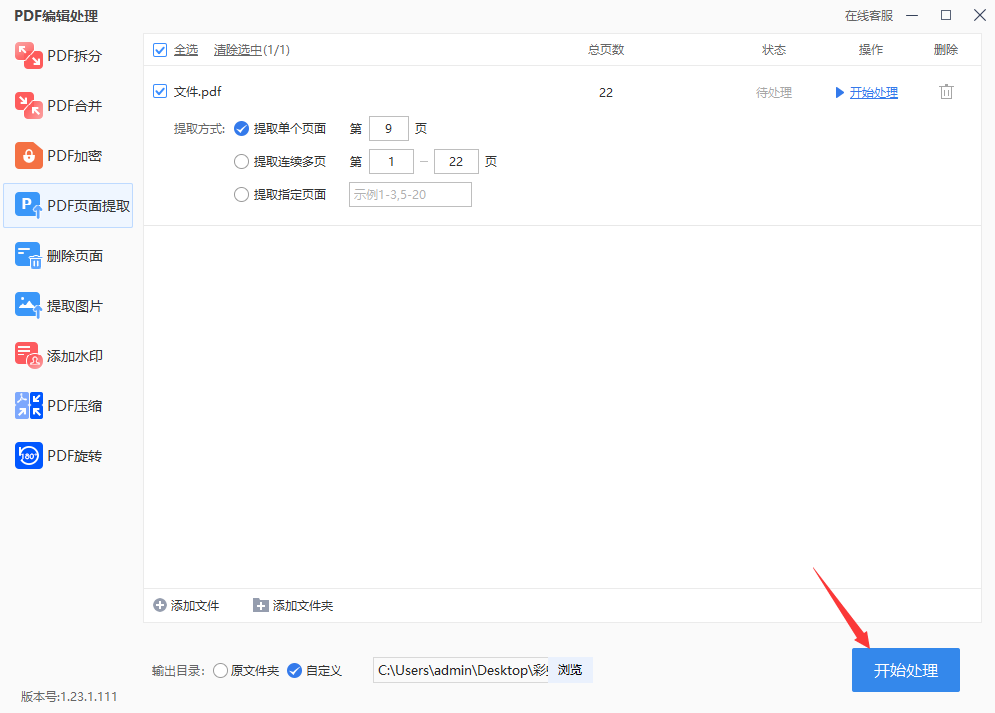
怎么把pdf中的某一页分出来?
怎么把pdf中的某一页分出来?PDF格式的文档在日常生活中是非常常见的,相信大家都对其有所了解,并且经常使用。它的主要特点是不允许用户随意编辑其中的内容,当我们仅需要阅读时,PDF文档无疑是十分方便的,尤其…...
MongoDB 聚合操作Map-Reduce
这此之前已经对MongoDB中的一些聚合操作进行了详细的介绍,主要介绍了聚合方法和聚合管道;如果您想对聚合方法和聚合管道进行了解,可以参考: MongoDB 数据库操作汇总https://blog.csdn.net/m1729339749/article/details/130086022…...

shiro CVE-2016-4437 漏洞复现
shiro Apache Shiro是一个强大且易用的Java安全框架,执行身份验证、授权、密码和会话管理。使用Shiro的易于理解的API,您可以快速、轻松地获得任何应用程序,从最小的移动应用程序到最大的网络和企业应用程序漏洞原理 在Apache shiro的框架中,执行身份验证时提供了…...

Seqkit-2.2.0 移植指南(openEuler 20.03 LTS SP3)
1.软件介绍 seqkit是一种跨平台的、极快的,全面的fasta/q处理工具。seqkit为所有的主流操作系统提供了一种可执行的双元文件,包括Windows,Linux,MacOS X,并且不依赖于任何的配置或预先配置就可以直接使用。 关于seqk…...
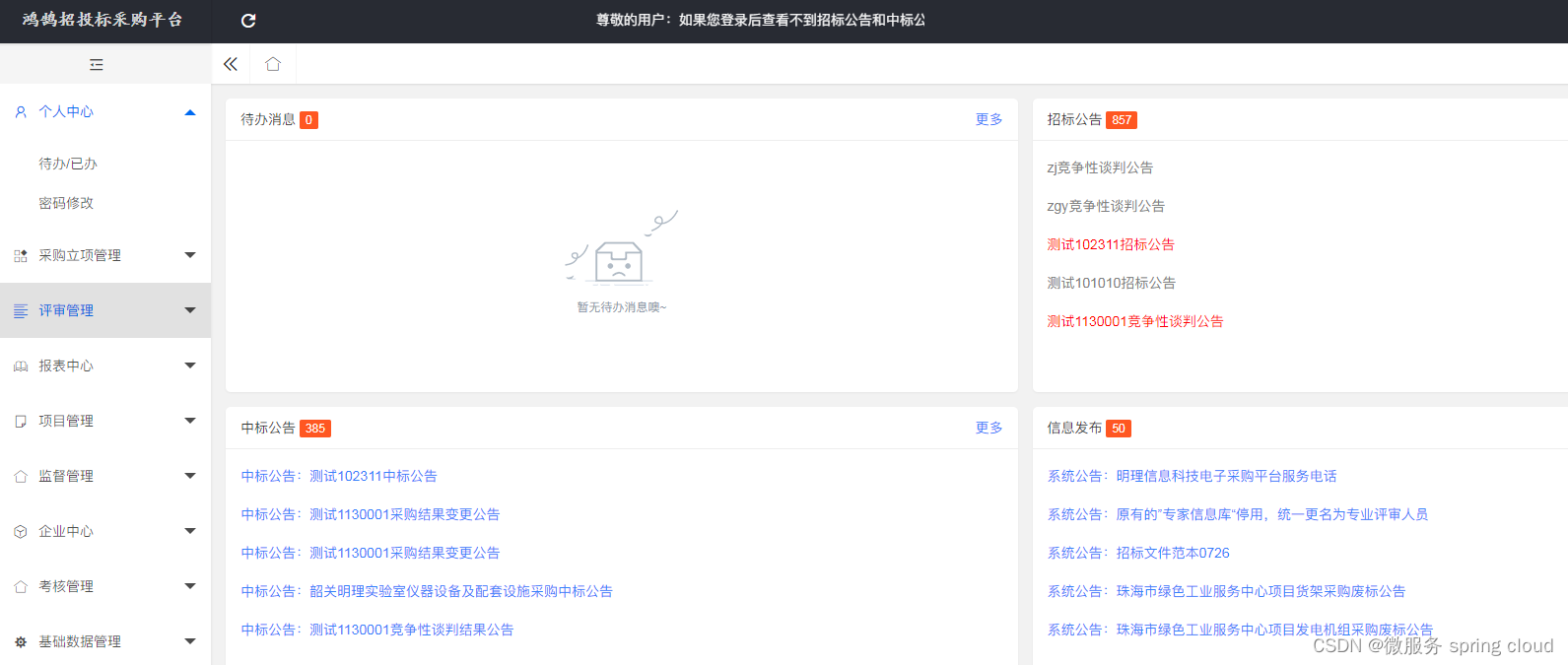
Java版本企业电子招投标采购系统源码——功能模块功能描述+数字化采购管理 采购招投标
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外部供…...
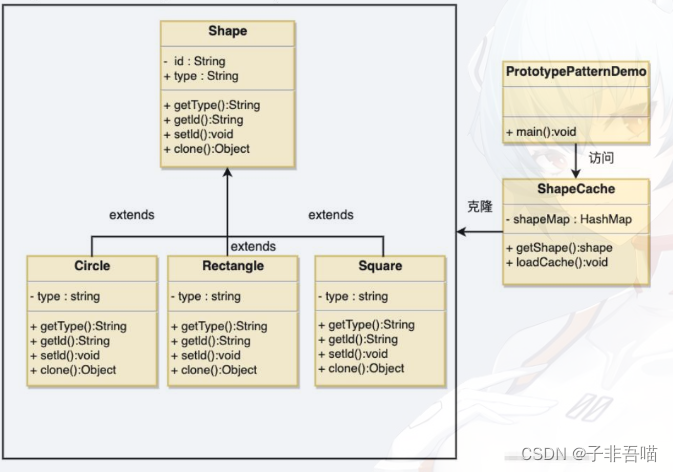
二十三种设计模式第五篇--原型模式
原型模式(Prototype Pattern)是用于创建重复的对象,同时又能保证性能。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。 这种模式是实现了一个原型接口,该接口用于创建当前对象的克隆。当直接创建…...
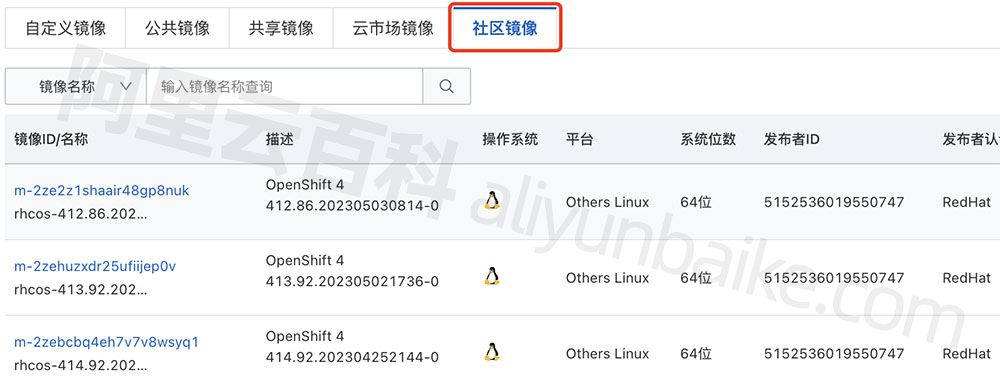
阿里云镜像区别公共镜像、自定义、共享、云市场和社区镜像介绍
阿里云服务器镜像根据来源不同分为公共镜像、自定义镜像、共享镜像、云市场镜像和社区镜像,一般没有特殊情况选择公共镜像,公共镜像是阿里云官网提供的正版授权操作系统,云市场镜像是在纯净版操作系统的基础上预装了相关软件及运行环境&#…...

非线性方程二分法
非线性方程二分法 优点:算法直观、简单、总能保证收敛;局限:收敛速度慢、一般不单独用它求根,仅为了获取根的粗略近似 文章目录 非线性方程二分法[toc]1 二分法基本思想2 二分法实现 1 二分法基本思想 设 f ( x ) f(x) f(x)在 [ …...
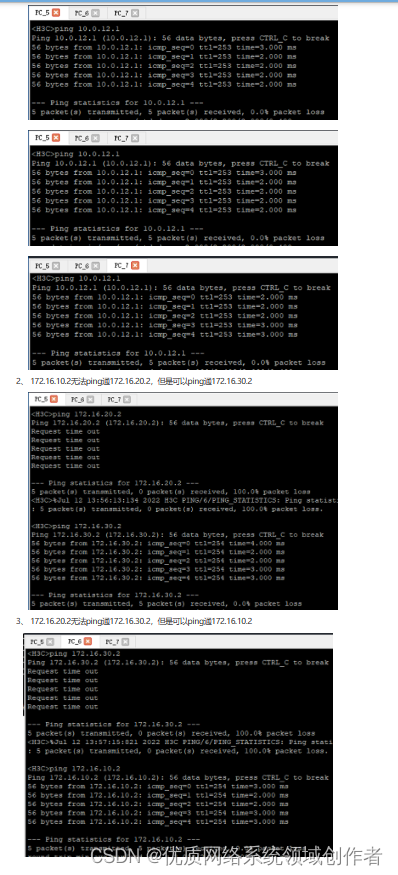
H3C防火墙单机旁路部署(网关在防火墙)
防火墙旁路部署在核心交换机上,内网有三个网段vlan 10:172.16.10.1/24、vlan 20:172.16.20.1/24、vlan30:172.16.30.1。要求内网网关在防火墙设备上,由防火墙作为DHCP服务器给终端下发地址,同时由防火墙来控…...
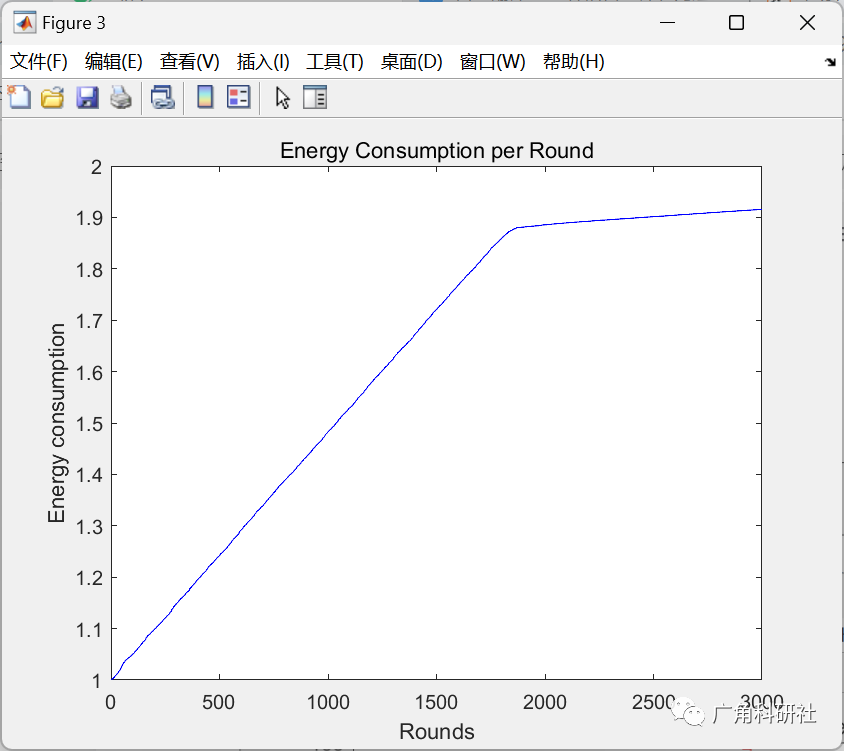
基于密度的无线传感器网络聚类算法的博弈分析(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 提高能源效率是无线传感器网络面临的关键挑战之一,无线传感器网络日益普遍。由于节点(传感器ÿ…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
