C# | 对象池

对象池
文章目录
- 对象池
- 前言
- 什么是对象池
- 对象池的优点
- 对象池的缺点
- 实现思路
- 示例代码
- 结束语
前言
当我们开发一个系统或者应用程序时,我们通常需要创建很多的对象,这些对象可能是线程、内存、数据库连接、文件句柄等等。在某些情况下,我们需要频繁地创建和销毁这些对象,这样会导致系统的性能下降和资源的浪费。这时,我们就可以使用对象池来管理这些对象,让它们可以被重复使用,从而提高程序的运行效率。
什么是对象池
那么,什么是对象池呢?简单来说,对象池就是预先创建一定数量的对象,并将它们存储在一个池中,当需要使用对象时,从对象池中获取一个对象,并在使用完毕后将其放回池中,以便可以多次重复使用。
对象池的优点
对象池可以大幅度减少对象的创建和销毁次数,从而提高程序的运行效率和资源的利用率。同时,它还可以避免内存碎片和资源的浪费,提高系统的稳定性和可扩展性。
对象池的缺点
使用对象池也有一些劣势,对象池需要占用一定的内存空间,如果对象的数量过多,可能会导致系统的内存不足。而且对象池需要进行对象的管理和维护,如果管理不当,可能会导致对象池的效率下降或者出现竞争条件等问题。
实现思路
设计对象池的思路主要是确定对象池的大小、对象的创建方式、对象的回收方式以及线程安全等问题。通常情况下,我们需要在程序初始化时创建一定数量的对象,并将这些对象存储在对象池中。
当需要使用对象时,从对象池中获取一个可用的对象,使用完毕后将其放回对象池中。如果对象池中的对象数量不足,可以根据需要动态地创建新的对象并添加到对象池中。
示例代码
下面是一个使用C#实现简易对象池的例子:
public class ObjectPool<T>
{private readonly Func<T> _objectFactory;private readonly ConcurrentBag<T> _objects;public ObjectPool(Func<T> objectFactory){_objectFactory = objectFactory;_objects = new ConcurrentBag<T>();}public T GetObject(){T obj;if (_objects.TryTake(out obj)){return obj;}return _objectFactory();}public void PutObject(T obj){_objects.Add(obj);}
}
上面的代码实现了一个简单的对象池,使用了C#中的ConcurrentBag类来实现线程安全的对象管理。在创建ObjectPool对象时,需要传入一个用于创建对象的委托函数。当需要获取对象时,先尝试从对象池中获取一个可用的对象,如果对象池中没有可用的对象,则根据委托函数创建一个新的对象。使用完毕后,将对象放回对象池中。
接下来优化一下这个例子,添加一个值限制对象池中保留对象的个数,超出限制的对象会被释放掉。
public class ObjectPool<T>
{private readonly Func<T> _objectFactory;private readonly ConcurrentBag<T> _objects;private readonly int _maxSize;public ObjectPool(Func<T> objectFactory, int maxSize){_objectFactory = objectFactory;_objects = new ConcurrentBag<T>();_maxSize = maxSize;}public T GetObject(){T obj;if (_objects.TryTake(out obj)){return obj;}return _objectFactory();}public void PutObject(T obj){if (_objects.Count < _maxSize){_objects.Add(obj);}else{IDisposable disposable = obj as IDisposable;if (disposable != null){disposable.Dispose();}}}
}
新增了一个名为_maxSize的属性来表示对象池中最多可以保留的对象个数。在PutObject方法中,我们判断当前对象池中的对象数量是否已经达到了最大值,如果是,则释放掉超出限制的对象,否则将对象加入到对象池中。为了保证释放对象时的安全性和可靠性,我们将对象转换为IDisposable接口,如果对象实现了IDisposable接口,则调用其Dispose方法进行释放。
这样,我们就成功地为对象池添加了一个值限制,可以避免对象池中的对象数量过多导致内存溢出和性能下降的问题。当对象池中的对象数量超过限制时,我们可以选择释放对象或者将对象丢弃掉,以保证程序的稳定性和可靠性。
结束语
通过使用对象池,我们可以大幅度减少对象的创建和销毁次数,从而提高程序的运行效率和资源的利用率。同时,我们也需要考虑对象池的大小和限制等问题,以保证程序的性能和可靠性。
在未来的文章中还会介绍其他相关的池,例如线程池、内存池等,更全面地讲解池的相关知识。
如果您觉得本文对您有所帮助,欢迎点赞收藏关注。谢谢!
禁止转载声明:
本文受到版权保护,未经作者许可,严禁转载。任何机构或个人不得以任何形式将本文用于商业用途或进行二次创作、复制、转载等行为。任何未经授权使用本文所涉及的任何内容,作者保留追究法律责任的权利。如需引用本文,请务必注明出处并获得作者的明确授权。本文刊载于[https://blog.csdn.net/lgj123xj],感谢您的理解与支持!
相关文章:

C# | 对象池
对象池 文章目录 对象池前言什么是对象池对象池的优点对象池的缺点 实现思路示例代码 结束语 前言 当我们开发一个系统或者应用程序时,我们通常需要创建很多的对象,这些对象可能是线程、内存、数据库连接、文件句柄等等。在某些情况下,我们需…...

CSS小技巧之圆形虚线边框
虚线相信大家日常都用的比较多,常见的用法就是使用 border-style 控制不同的样式,比如设置如下边框代码: border-style: dotted dashed solid double;这将设置顶部的边框样式为点状,右边的边框样式为虚线,底部的边框样…...

QString与QByteArray互相转换的方法
QString与QByteArray互相转换的方法 [1] QString与QByteArray互相转换的方法QString转QByteArray方法QByteArray转QString方法QByteArray类同样不以’\0’为结尾QByteArray转QString,主要用buf.toHex()即可 [2] Qt开发串口通讯软件中的数据转换问题1.读取串口命令-Q…...

Springboot +Flowable,设置流程变量的方式(一)
一.简介 为什么需要流程变量。 举个例子,假设有如下一个流程,截图如下: 这是一个请假流程,那么谁请假、请几天、起始时间、请假理由等等,这些都需要说明,不然领导审批的依据是啥?那么如何传递…...
机器学习13(正则化)
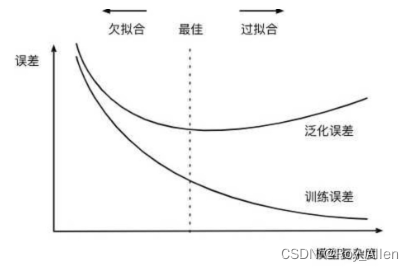
文章目录 简介正则化经验风险和结构风险过拟合正则化建模策略 逻辑回归逻辑回归评估器 练习评估器训练与过拟合实验评估器的手动调参 简介 这一节详细探讨关于正则化的相关内容,并就 sklearn 中逻辑回归(评估器)的参数进行详细解释由于 skle…...
:原子数组、)
并发编程学习(十一):原子数组、
1、数组类型的原子类 原子数组类型,这个其实和AtomicInteger等类似,只不过在修改时需要指明数组下标。 CAS是按照来根据地址进行比较。数组比较地址,肯定是不行的,只能比较下标元素。而比较下标元素,就和元素的…...
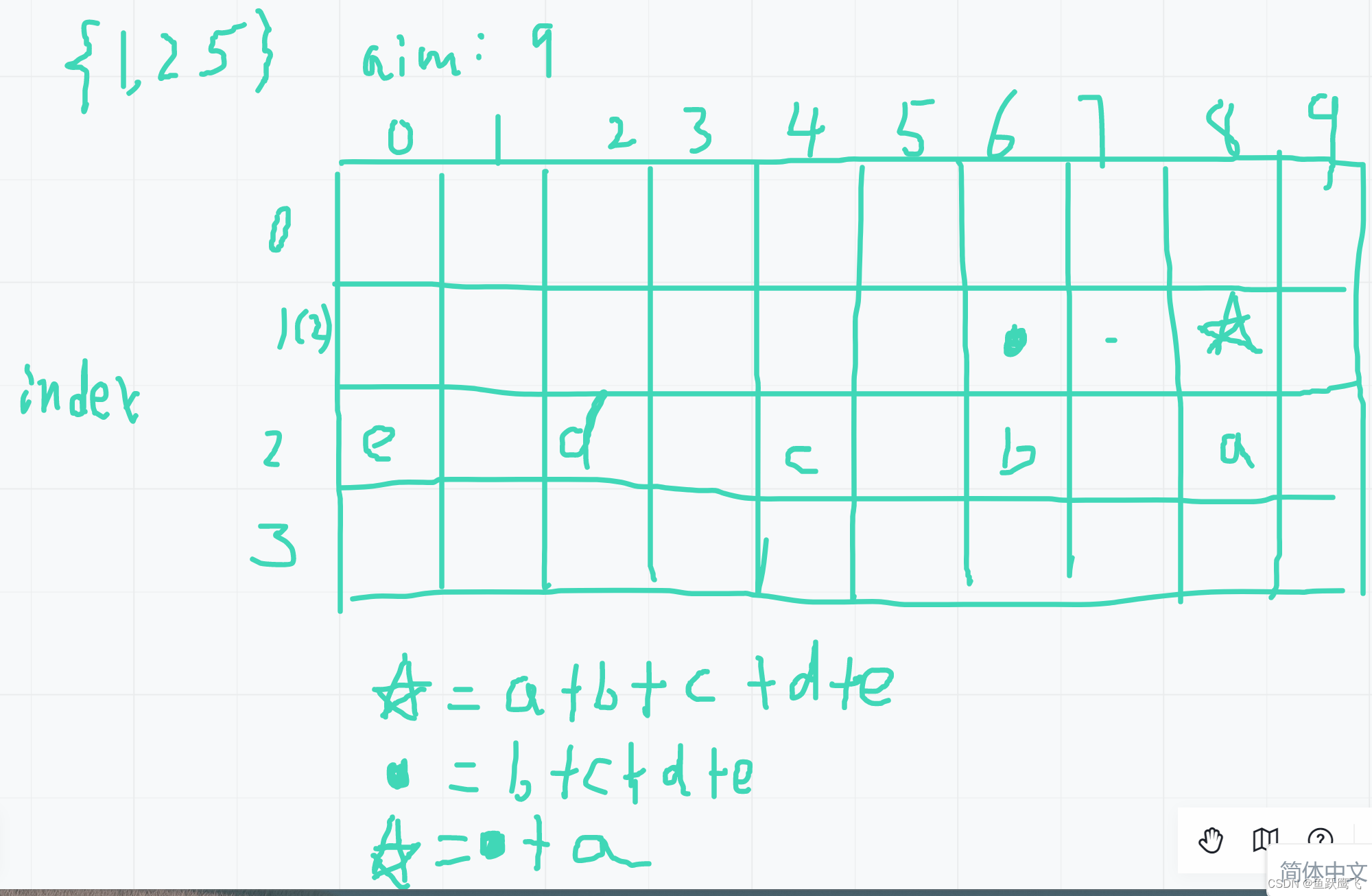
递归到动态规划:省去枚举行为
如果在动态规划的过程中没有枚举行为,那严格位置依赖和傻缓存的方式并没有太大区别,但是当有枚举行为的时候(一个位置依赖于多个位置),那严格位置依赖是有优化空间的,枚举行为也许可以省去,题目…...

服务(第二十一篇)mysql高级查询语句(二)
①视图表: 视图表是虚拟表,用来存储SQL语句的定义 如果视图表和原表的字段相同,是可以进行数据修改的; 如果两者的字段不通,不可以修改数据。 语法: 创建:create view 试图表名 as ... 查…...

MYSQL高可用配置(MHA)
1、什么是MHA MHA(Master High Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…...

单精度浮点数与十进制数据相互转换
一、float基础: Float类型占4个字节,也就是32bit,其中最高位是符号位,2~9位是指数位,后边的23bit是数值位.如下所示 大部分数据的二进制形式都可以用科学计数法表示,即1.m*2^n这种形式,只要知道m和n,就能确定一个数值 二、小数位如何转变为二进制: 下面…...

PMP敏捷-4大价值观、12原则
宣言及4大价值观 个体及互动 胜于 流程和工具 以人为本 工作的软件 胜于 完整的文档 以价值为导向 客户合作 胜于 合同谈判 合作共赢 应对变更 胜于 遵循计划 拥抱变化 12原则 工作原则:精益、至简,实现这种原则的方式是“定期反省”。9、10、12 …...
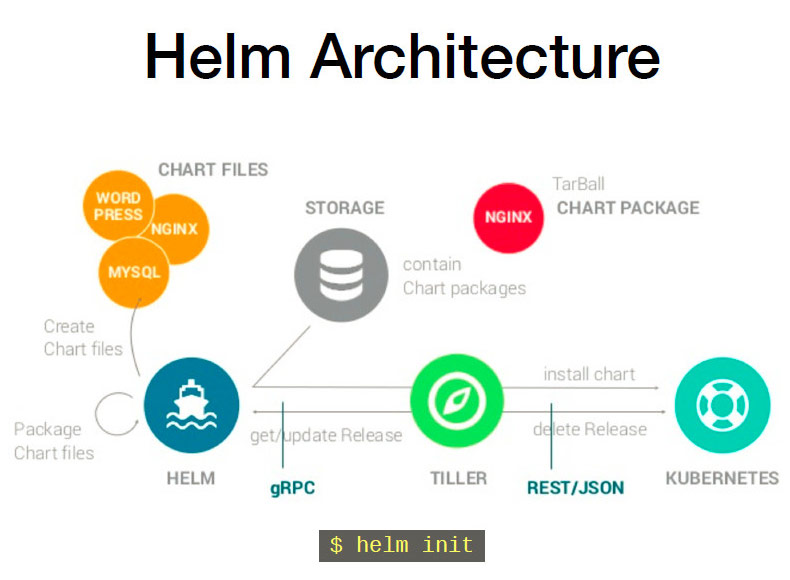
K8S—Helm
一、Helm介绍 helm通过打包的方式,支持发布的版本管理和控制,很大程度上简化了Kubernetes应用的部署和管理。 Helm本质就是让k8s的应用管理(Deployment、Service等)可配置,能动态生成。通过动态生成K8S资源清单文件&a…...

ALSA内部函数调用流程
ALSA内部函数调用流程 一直都有这样的一个疑问 就是在linux系统中我们调用snd_pcm_open后,就不知道alsa内部是怎么运行的了 用户的pcm_open()相当于先对ASoC各个驱动模块startup(),再做hw_params()。 pcm_open()pcm->fd open("/dev/snd/pcm…...

Python正则表达式详解,保姆式教学,0基础也能掌握正则
正则作为处理字符串的一个实用工具,在Python中经常会用到,比如爬虫爬取数据时常用正则来检索字符串等等。正则表达式已经内嵌在Python中,通过导入re模块就可以使用,作为刚学Python的新手大多数都听说”正则“这个术语。 今天来给…...

ChatGPT 接入飞书教程,创建自己的聊天机器人
ChatGPT 接入飞书教程,创建自己的聊天机器人 一、飞书进入开发者平台。点击创建应用。二、打开Aircode,点击创建应用,上面输入名字,下面选择Node.js v16三、配置环境,点击Environments,创建四个变量,全部要大写本教程收集于: AIGC从入门到精通教程 首先,准备三个账号…...
)
JS生成随机数(多种解决方案)
JS生成随机数 概述 随机数是编程语言中的重要组成部分。在JavaScript中,生成随机数是一项简单的任务。本文将介绍生成随机数的各种方法。 Math.random() Math.random()是JavaScript中生成随机数最常见的方法。该方法返回介于0和1之间的随机数。例如,…...

文件IO 函数 静态库和动态库的创建 5.11
5.11 文件IO函数 1.数据读写 ssize_t read(int fd,void *buf,size_t count); 功能: 从fd对应的文件中 读取前count个字节的数据到buf缓冲区中 头文件: #include <unistd.h> 参数: fd :文件描述符 buf…...

考研日语-详解ている、てある、ていく、てくる用法
目录 一、ている用法 1. 表示现在状态 2. 表示持续动作 3. 表示经验或习惯 4. 表示结果或效果 二、てある用法 1. 表示已经完成的动作 2. 表示现在状态 3. 表示被动 三、ていく用法 1. 表示未来的动作 2. 表示逐渐变化的过程 四、てくる用法 1. 表示过去到现在的…...

Spring Security 6.x 系列【36】授权服务器篇之OpenID Connect 1.0
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 3.0.4 本系列Spring Security 版本 6.0.2 本系列Spring Authorization Server 版本 1.0.2 源码地址:https://gitee.com/pearl-organization/study-spring-security-demo 文章目录 1. 前言2. OpenID Connect…...
【计算机视觉 | Pytorch】timm 包的具体介绍和图像分类案例(含源代码)
一、具体介绍 timm 是一个 PyTorch 原生实现的计算机视觉模型库。它提供了预训练模型和各种网络组件,可以用于各种计算机视觉任务,例如图像分类、物体检测、语义分割等等。 timm 的特点如下: PyTorch 原生实现:timm 的实现方式…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

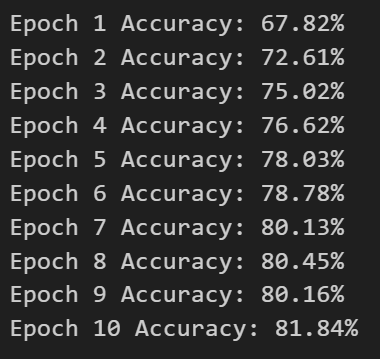
拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...
