Cpython的多线程技术之痛
历史原因
在Python官网下载的默认解释器是采用C语言编写的Cpython解释器。在Python语言开发之初,计算机都是单核CPU,每个单核CPU同一时刻只能运行一个线程。为了模拟多线程工作,这里采用了模拟机制,让不同线程根据时间片段,轮流着去执行数据,使多线程具有相对均衡的时间机会使用CPU计算资源。基于当时的CPU技术,python语言发明人采用了单核CPU技术进程技术。为了保证线程执行的安全,在Cpython解释器上提供了全局解释器锁(Global Interpreter Lock,GIL),当在Cpython解释器上执行python代码时,GIL会保护代码的线程独立使用共享数据,直到解释器遇到I/O操作或者操作次数达到一定数目时才会释放GIL。所以Cpython解释器整体作为一个进程,同一时间只有一个获得GIL保护的线程在执行,其他线程则处于等待状态。由此,得出Cpython解释器下多线程执行的结论。
1、Cpython解释器环境下的python语言只存在模拟多线程状态,不存在真正的并发多线程。也就是说,在多核CPU情况下,无法利用多喝同时执行多个线程,以提高执行效率。
2、Cpython受全局解释器锁保护,提供了模拟多线程执行安全,但是无法实现真正的并发多线程。
3、多线程有两个应用方向,即CPU-bound(计算密集型)和I/Obound(I/O密集型)。计算密集型任务主要通过多线程,充分利用CPU的资源(特别是多核计算资源)解决特定复杂计算问题,如复杂的科学计算算法。I/O密集型任务主要通过多线程,对磁盘I/O、网络I/O进行读写处理,CPU计算任务比较小。这符合GIL快速锁定、快速释放特点。
由此可以得出CPython解释器环境下易执行I/O多线程操作,避免利用它做CPU多线程操作。
所以在CPython解释器下执行的多线程都受GIL这把全局锁保护,使多线程在某一时刻访问数据共享资源时,只能允许一个线程执行。这样保证了线程之间的安全,避免了数据共享资源的冲突,但是做不到真正的多线程并发处理。(其实Cpython的GIL问题是Python开源社区最难解决、最头疼的问题,为了避开其多线程技术的缺陷,甚至有专家建议用其他方法代替。)
python的多线程技术的替代方案
1、采用Jython、IronPython、PyPy等其他解释器。上述几种解释器不受GIL约束,实现了真正意义上的多线程并发技术。
2、利用ctypes模块绕过GIL约束。ctypes提供了在Python语言环境下调用C语言动态库的能力。借助C语言函数的功能实现对多内核CPU的使用。ctypes模块使用C语言方法,详见官网提供的《Python使用文档》的标准库相关文章内容。
3、利用multiprocessing模块、
subprocess模块
子进程模块允许通过产生新的进程连接到它们的输入、输出、错误管道中,并获得它们的返回代码。该模块旨在替换几个较旧的模块和功能。
sched模块、
调度模块定义了一个实现通用事件调度器的类。
4、concurrent模块,concurrent.futures模块为异步执行可调用对象提供了一个高级接口。该模块的ProcessPoolExecutor类可被用来在一个单独的Python解释器中执行计算密集型函数,并在多核CPU里并行执行。
5、不同编程语言有不同编程语言的应用优势,显然Python在多线程编程方面存在一些缺陷。如果纯粹为了解决多线程编程和应用问题,也可以选择其他功能更加强大的编程语言,如C、C++、Java等。
相关文章:

Cpython的多线程技术之痛
历史原因 在Python官网下载的默认解释器是采用C语言编写的Cpython解释器。在Python语言开发之初,计算机都是单核CPU,每个单核CPU同一时刻只能运行一个线程。为了模拟多线程工作,这里采用了模拟机制,让不同线程根据时间片段&#…...
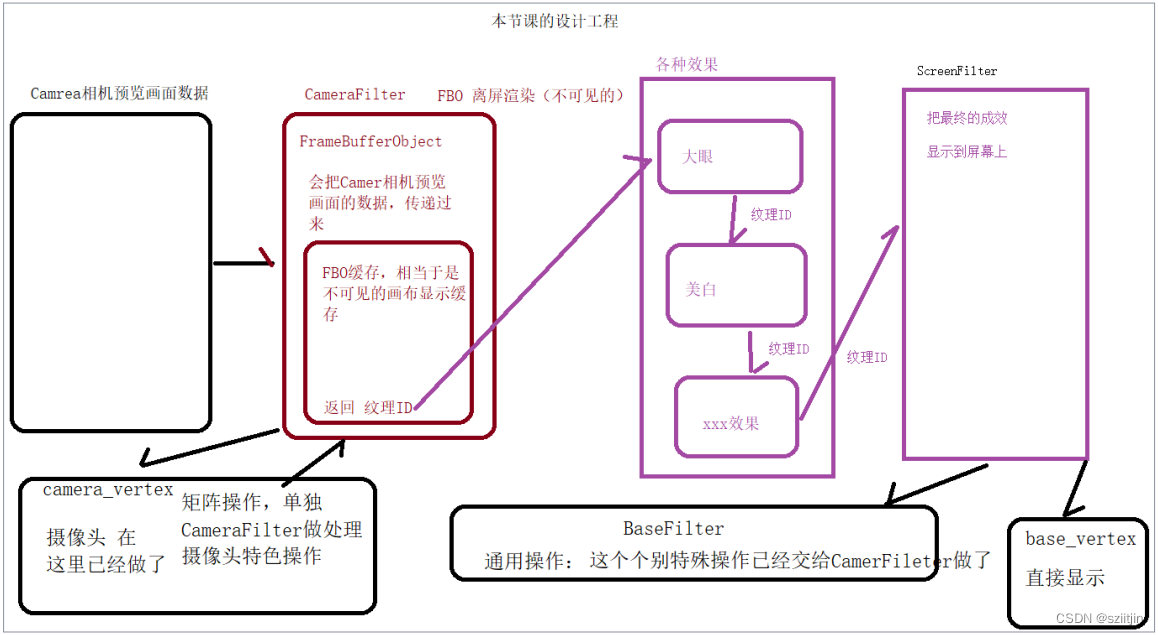
NDK OpenGL离屏渲染与工程代码整合
NDK系列之OpenGL离屏渲染与工程代码整合,本节主要是对上一节OpenGL渲染画面效果代码进行封装设计,将各种特效代码进行分离解耦,便于后期增加其他特效。 实现效果: 实现逻辑: 1.封装BaseFilter过滤器基类,…...

Python基础入门编程代码练习(二)
一、求1~100之间不能被3整除的数之和 循环条件:i<100循环操作 实现代码如下: def sums():sum 0for num in range(1, 101):if num % 3 ! 0:sum numprint("1~100之间不能被3整除的数之和为:%s" % (sum))sums() print("1~…...

C# | 对象池
对象池 文章目录 对象池前言什么是对象池对象池的优点对象池的缺点 实现思路示例代码 结束语 前言 当我们开发一个系统或者应用程序时,我们通常需要创建很多的对象,这些对象可能是线程、内存、数据库连接、文件句柄等等。在某些情况下,我们需…...

CSS小技巧之圆形虚线边框
虚线相信大家日常都用的比较多,常见的用法就是使用 border-style 控制不同的样式,比如设置如下边框代码: border-style: dotted dashed solid double;这将设置顶部的边框样式为点状,右边的边框样式为虚线,底部的边框样…...

QString与QByteArray互相转换的方法
QString与QByteArray互相转换的方法 [1] QString与QByteArray互相转换的方法QString转QByteArray方法QByteArray转QString方法QByteArray类同样不以’\0’为结尾QByteArray转QString,主要用buf.toHex()即可 [2] Qt开发串口通讯软件中的数据转换问题1.读取串口命令-Q…...

Springboot +Flowable,设置流程变量的方式(一)
一.简介 为什么需要流程变量。 举个例子,假设有如下一个流程,截图如下: 这是一个请假流程,那么谁请假、请几天、起始时间、请假理由等等,这些都需要说明,不然领导审批的依据是啥?那么如何传递…...
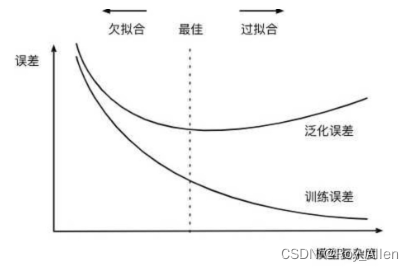
机器学习13(正则化)
文章目录 简介正则化经验风险和结构风险过拟合正则化建模策略 逻辑回归逻辑回归评估器 练习评估器训练与过拟合实验评估器的手动调参 简介 这一节详细探讨关于正则化的相关内容,并就 sklearn 中逻辑回归(评估器)的参数进行详细解释由于 skle…...
:原子数组、)
并发编程学习(十一):原子数组、
1、数组类型的原子类 原子数组类型,这个其实和AtomicInteger等类似,只不过在修改时需要指明数组下标。 CAS是按照来根据地址进行比较。数组比较地址,肯定是不行的,只能比较下标元素。而比较下标元素,就和元素的…...
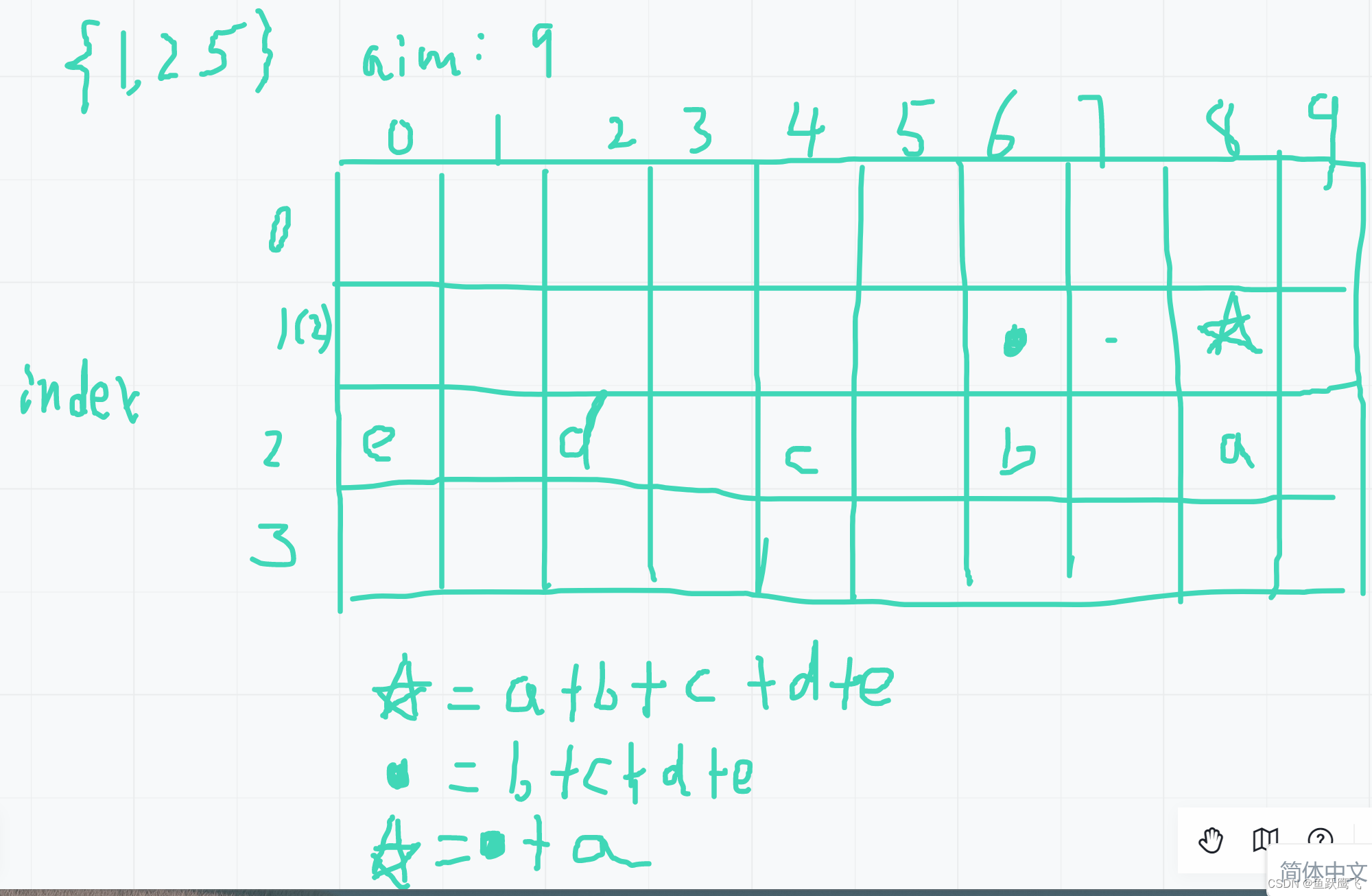
递归到动态规划:省去枚举行为
如果在动态规划的过程中没有枚举行为,那严格位置依赖和傻缓存的方式并没有太大区别,但是当有枚举行为的时候(一个位置依赖于多个位置),那严格位置依赖是有优化空间的,枚举行为也许可以省去,题目…...

服务(第二十一篇)mysql高级查询语句(二)
①视图表: 视图表是虚拟表,用来存储SQL语句的定义 如果视图表和原表的字段相同,是可以进行数据修改的; 如果两者的字段不通,不可以修改数据。 语法: 创建:create view 试图表名 as ... 查…...

MYSQL高可用配置(MHA)
1、什么是MHA MHA(Master High Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…...

单精度浮点数与十进制数据相互转换
一、float基础: Float类型占4个字节,也就是32bit,其中最高位是符号位,2~9位是指数位,后边的23bit是数值位.如下所示 大部分数据的二进制形式都可以用科学计数法表示,即1.m*2^n这种形式,只要知道m和n,就能确定一个数值 二、小数位如何转变为二进制: 下面…...

PMP敏捷-4大价值观、12原则
宣言及4大价值观 个体及互动 胜于 流程和工具 以人为本 工作的软件 胜于 完整的文档 以价值为导向 客户合作 胜于 合同谈判 合作共赢 应对变更 胜于 遵循计划 拥抱变化 12原则 工作原则:精益、至简,实现这种原则的方式是“定期反省”。9、10、12 …...
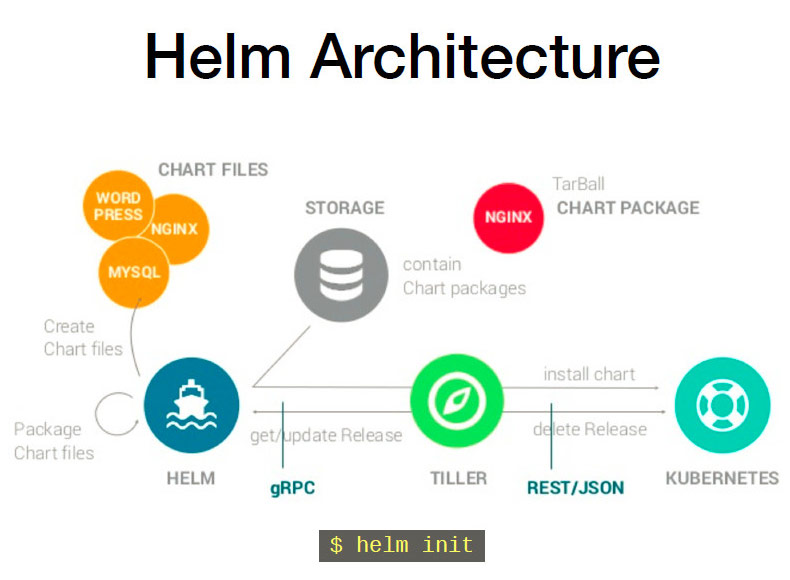
K8S—Helm
一、Helm介绍 helm通过打包的方式,支持发布的版本管理和控制,很大程度上简化了Kubernetes应用的部署和管理。 Helm本质就是让k8s的应用管理(Deployment、Service等)可配置,能动态生成。通过动态生成K8S资源清单文件&a…...

ALSA内部函数调用流程
ALSA内部函数调用流程 一直都有这样的一个疑问 就是在linux系统中我们调用snd_pcm_open后,就不知道alsa内部是怎么运行的了 用户的pcm_open()相当于先对ASoC各个驱动模块startup(),再做hw_params()。 pcm_open()pcm->fd open("/dev/snd/pcm…...

Python正则表达式详解,保姆式教学,0基础也能掌握正则
正则作为处理字符串的一个实用工具,在Python中经常会用到,比如爬虫爬取数据时常用正则来检索字符串等等。正则表达式已经内嵌在Python中,通过导入re模块就可以使用,作为刚学Python的新手大多数都听说”正则“这个术语。 今天来给…...

ChatGPT 接入飞书教程,创建自己的聊天机器人
ChatGPT 接入飞书教程,创建自己的聊天机器人 一、飞书进入开发者平台。点击创建应用。二、打开Aircode,点击创建应用,上面输入名字,下面选择Node.js v16三、配置环境,点击Environments,创建四个变量,全部要大写本教程收集于: AIGC从入门到精通教程 首先,准备三个账号…...
)
JS生成随机数(多种解决方案)
JS生成随机数 概述 随机数是编程语言中的重要组成部分。在JavaScript中,生成随机数是一项简单的任务。本文将介绍生成随机数的各种方法。 Math.random() Math.random()是JavaScript中生成随机数最常见的方法。该方法返回介于0和1之间的随机数。例如,…...

文件IO 函数 静态库和动态库的创建 5.11
5.11 文件IO函数 1.数据读写 ssize_t read(int fd,void *buf,size_t count); 功能: 从fd对应的文件中 读取前count个字节的数据到buf缓冲区中 头文件: #include <unistd.h> 参数: fd :文件描述符 buf…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
