14.贪心算法
一、算法内容
1.简介
贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择,而不考虑后续可能造成的影响。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
在贪心算法的应用当中,往往都会和排序联系起来,所以想要熟练使用贪心算法则必须首先能够熟练地应用排序。而由于贪心算法采取的是局部最优策略,故如果使用贪心算法之前往往需要证明算法的正确性,即证明在此题目/事件中,在每一步采取局部最优策略会得到整体最优的结果。
2.对比与联系
与此算法相对应的是后续我们会学到的动态规划,在动态规划中我们则必须要考虑一个选择对后续的影响。
贪心算法的应用非常广泛,很多其他的算法都需要贪心算法来作为基础。例如:哈夫曼编码、 K r u s k a l Kruskal Kruskal算法、 P r i m Prim Prim算法、 A ∗ A^* A∗算法等等。所以学好贪心算法是非常重要。
二、实例分析
1.最简单的例子
下面我们将以洛谷上的题目P1208为例,讲解贪心算法的最简单的使用方式。
(1)题目大意
- 公司需要收购一定量的牛奶
- 每一个奶农能卖出的牛奶的量和价格都不同
- 公司希望能以最少的钱买到足够量的牛奶
(2)题目分析
显然按照题目意思,我们只需要将牛奶价格排序好,然后从价格低的开始买,如果此价格的牛奶已经没了,那么才购买价格更高的牛奶,一直买到满足公司收购的量为止即可。
本题目的贪心非常浅显易懂,这里不再给出证明。
(3)正解程序
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdlib>
#include <cstdio>using namespace std;
typedef long long ll;
const ll maxn=5010;
ll n,m,ans=0;
struct node
{ll per,num;
}farmer[maxn];
bool cmp(node x,node y)
{if(x.per!=y.per)return x.per<y.per;elsereturn x.num>y.num;
}
int main()
{scanf("%lld%lld",&n,&m);for(ll i=1;i<=m;i++)scanf("%lld%lld",&farmer[i].per,&farmer[i].num);sort(farmer+1,farmer+1+m,cmp);ll pos=1;while(n){if(farmer[pos].num!=0){farmer[pos].num--;ans+=farmer[pos].per;n--;}elsepos++;}printf("%lld\n",ans);return 0;
}
2.稍微复杂一点的例子
下面我们将以洛谷上的题目P1094为例,讲解贪心算法的进一步应用,并给出证明的思路。
(1)题目大意
- 有一组物品需要进行分组,每个物品都有一个价格
- 希望保证每一组的价格总和小于某一固定值的情况下,使得分组数尽量小
- 每一组最多包含两个物品
(2)题目分析
- 首先我们能够想到,要使分组数尽可能小,那么一定是尽量两两组合
- 所以我们很容易能够想到一个贪心思路,那就是将物品按价格从小到大排序,然后尽量用价格小的和价格大的进行组合。
- 可以提前说明的是,这个贪心思路是正确的,然而问题并没有完全解决,为什么这样组合之后就能使得最后的分组数最小呢?
(3)贪心证明
-
根据我们前面所讲到的点,将使用反证法证明
-
设价格总和上限为 X X X,现有四个物品的价格为 v a , v b , v c , v d v_a,v_b,v_c,v_d va,vb,vc,vd,按从小到大排序
-
若 v a + v d ≤ X , v b + v c ≤ X v_a+v_d\leq X,v_b+v_c\leq X va+vd≤X,vb+vc≤X,此为贪心法得到的分组,最少分为两组。下面改变组合方式,因为 v a + v c ≤ X v_a+v_c\leq X va+vc≤X显然成立,所以仅考虑另一组的情况。
- 若 v b + v d ≤ X v_b+v_d\leq X vb+vd≤X,那么可以分为两组
- 若 v b + v d ≤ X v_b+v_d\leq X vb+vd≤X,那么仅能分为一组。因为 v a ≤ v b v_a\leq v_b va≤vb,所以此处情况完全可能出现。
-
若 v a + v d > X v_a+v_d> X va+vd>X则无论如何都只能分为一组
-
若 v a + v d ≤ X , v b + v c > X v_a+v_d\leq X,v_b+v_c> X va+vd≤X,vb+vc>X。下面考虑 v a + v c , v b + c d v_a+v_c,v_b+c_d va+vc,vb+cd这一种组合方式,显然 v b + v d > X v_b+v_d>X vb+vd>X,所以无论怎么分仍然只有一组。
-
可以看到,非贪心的情况有可能导致答案数变少。例如 v a = 1 , v b = 5 , v c = 6 , v d = 8 , X = 11 v_a=1,v_b=5,v_c=6,v_d=8,X=11 va=1,vb=5,vc=6,vd=8,X=11
(4)正解程序
#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <cstdlib>
#include <cstdio>using namespace std;
typedef long long ll;
const ll maxn=1000010;
ll num[maxn],ans;
int main()
{ll n,w;scanf("%lld%lld",&w,&n);for(ll i=0;i<n;i++)scanf("%lld",&num[i]);sort(num,num+n);ll z=0,y=n-1;while(z<=y){if(num[z]+num[y]<=w){ans++;z++;y--;}else{y--;ans++;}}printf("%lld\n",ans);return 0;
}
三、作业
1.基础题
P1094 [NOIP2007 普及组] 纪念品分组
P1208 [USACO1.3]混合牛奶 Mixing Milk
P3817 小A的糖果
P5019 [NOIP2018 提高组] 铺设道路
2.提高题
P1056 [NOIP2008 普及组] 排座椅
P1199 [NOIP2010 普及组] 三国游戏
相关文章:

14.贪心算法
一、算法内容 1.简介 贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择,而不考虑后续可能造成的影响。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。 贪心算法不是对所有问题都能得到整体最优…...

你知道营销人为什么要讲洞察吗?
用户洞察,是制定品牌和产品战略的基础,基于深刻的用户洞察,才能谈价值发现,目标规划,产品设计,全方位运营等。 可以这么说,没有洞察就没有营销,因为你的营销策略不能凭空想象&#…...
Neovim-配置教程
环境:Ubuntu 20.04 宿主机:windows (windows terminal)WSL2 NVIM:v0.10.0-dev 配置Neovim 需要保证流畅的github环境(以便于快速拉取插件),可以使用代理或是配置Github SSH key 本文…...
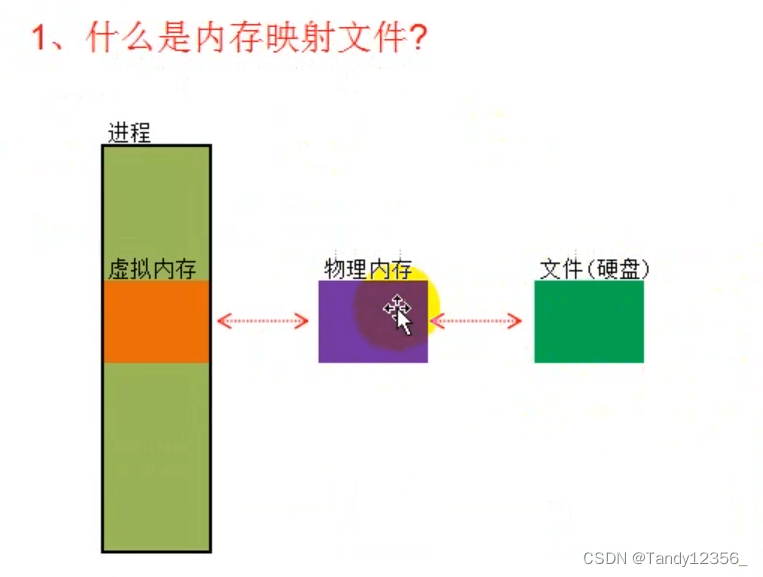
Windows管理内存的3种方式——堆、虚拟内存、共享内存
一、操作系统管理内存概述 在 Windows 操作系统中,每个进程都被分配了 4GB 的虚拟地址空间,这被称为进程的虚拟地址空间。虚拟地址空间提供了一个抽象的地址空间,使得每个进程都可以认为它拥有自己的独立内存空间。这个虚拟地址空间被分为两…...

PCM/FM解调原理与Matlab算法仿真
调制的作用是将调制信息的频谱从低频搬移到高频,以适合信道传输。关于调制的原理,在上一节中已经讲过了。在这一节中,主要讲解FM的解调原理。与调制相对应的是在接收端需要解调过程将调制信息复原,所以解调是影响通信系统性能的重要技术。 解调方法按照是否需要载波恢复的…...

我的『1024』创作纪念日
目录 ◐机缘 ◑收获 ◐日常 ◑成就 ◐憧憬 记得,2020年07月22日我撰写了第1篇技术博客:《遗传算法实例解析》在这平凡的一天,我赋予了它不平凡的意义也许是立志成为一名专业T作者、也许是记录一段刚实践的经验但在那一刻,我已…...
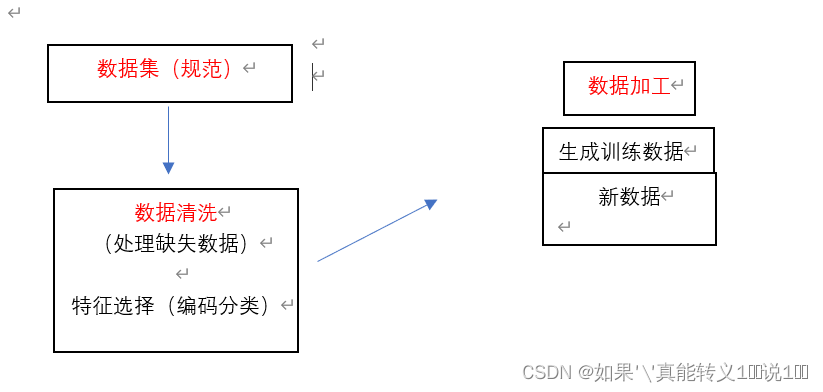
Python ---> 衍生的数据技术
我的个人博客主页:如果’真能转义1️⃣说1️⃣的博客主页 关于Python基本语法学习---->可以参考我的这篇博客:《我在VScode学Python》 随着人工智能技术的发展,挖掘和分析商业运用大数据已经成为一种推动应用, 推动社会发展起着…...

【27】linux进阶——rpm软件包的管理
大家好,这里是天亮之前ict,本人网络工程大三在读小学生,拥有锐捷的ie和红帽的ce认证。每天更新一个linux进阶的小知识,希望能提高自己的技术的同时,也可以帮助到大家 另外其它专栏请关注: 锐捷数通实验&…...
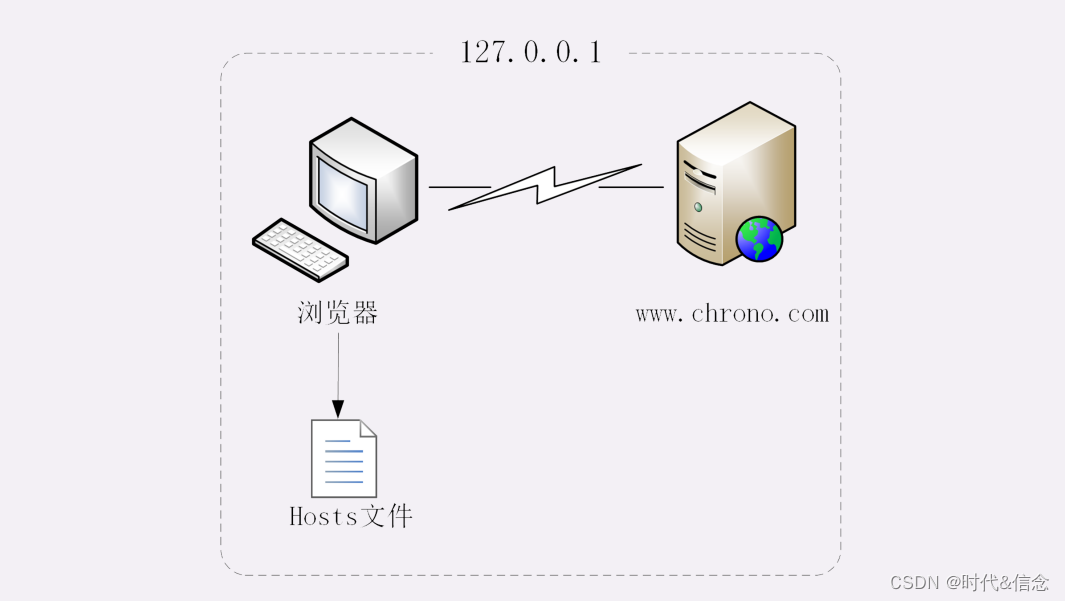
HTTP第六讲——键入网址再按下回车,后面究竟发生了什么?
使用 IP 地址访问 Web 服务器 首先我们运行 www 目录下的“start”批处理程序,启动本机的 OpenResty 服务器,启动后可以用“list”批处理确认服务是否正常运行。 然后我们打开 Wireshark,选择“HTTP TCP port(80)”过滤器,再鼠标…...

layui目录和项目引入
1.目录结构如下 ├─css //css目录 │ │─modules //模块css目录(一般如果模块相对较大,我们会单独提取,比如下面三个:) │ │ ├─laydate │ │ ├─layer │ │ └─layim │ └─layui.css //核心样式文件…...

Ubuntu22.04 将EFI启动分区迁移到另一块硬盘
机器上有两块硬盘, 一块已经安装了Win10, 另一块新装Ubuntu22.04, 在新硬盘上划分分区的时候, 有分出256M给 BOOT EFI, 但是安装的时候没注意, 启动分区不知道怎的跑到 Windows 所在的硬盘上了 记录一下将 /boot/efi 分区迁移至 Ubuntu 所在硬盘, 并创建 Grub 的记录. 预留的…...

只要学会这些AI工具,一个人就是一家营销咨询公司
本教程收集于:AIGC从入门到精通教程 只要学会这些AI工具,一个人就是一家营销咨询公司 随着AI工具的不断涌现,您只需掌握市面上热门的AI工具,便可独自开展营销咨询公司。通过一系列AI工具,您可以为企业提供全案服务,收获丰厚回报。 例如,在协助一家美妆初创公司出海时,…...

[离散数学] 函数
文章目录 函数判断函数的条件复合函数复合函数的性质 逆函数 函数 判断函数的条件 dom F A ⇔ \Leftrightarrow ⇔所有x 都有 F(x)与之对应 有唯一的与其对应 < x , y > ∈ f ∧ < y , z > ∈ f ⇒ y z <x,y>\in f \land <y,z…...

好家伙,又一份牛逼笔记面世了...
最近网传的一些裁员的消息,搞的人心惶惶。已经拿到大厂offer的码友来问我:大厂还能去,去了会不会被裁。 还在学习的网友来问我:现在还要冲互联网么? 我是认为大家不用恐慌吧,该看啥看啥,该学啥…...
基于nodejs+vue3 的高仿网易云音乐
大家好,我是小寻,欢迎大家关注我的公众号:工具优选,加入前端、java群聊哦! 今天给大家分享一个超高水准的项目:基于nodejsvue3研发的高仿网易云音乐,项目内容出自寻码网! 技术栈&a…...
MySQL数据库用户管理以及数据库用户授权
一、数据库用户管理 1、新建用户 CREATE USER 用户名来源地址 [IDENTIFIED BY [PASSWORD] 密码]; ---------------------------------------------------------------------------------------------------------- 用户名:指定将创建的用户名 来源地址:…...

全面分析生物技术的优缺点以及应用场景
一、 引言 生物识别技术具有不可撤销性、高度便利性和较低错误率等优势,在安全领域中也备受瞩目。然而,对于生物识别技术在应对安全挑战方面的可靠性和有效性,但争议并未被完全解决 二、生物识别技术的介绍 所谓生物识别技术就是,…...

OpenAI是什么?
OpenAI是一家人工智能技术公司,成立于2015年,总部位于美国旧金山。它的创始人包括埃隆马斯克等多名知名人士,公司的目标是推进人工智能技术的发展,同时确保人工智能的发展不会对人类造成负面影响。 OpenAI在研究和开发各种人工智能…...

量子计算——新兴领域的前沿技术
随着人类社会文明的不断进步,计算技术也在不断发展。传统计算机在过去的几十年中快速发展,计算速度、存储能力等方面发生了天翻地覆的变化。但随着大数据、人工智能、区块链等新兴领域的迅速崛起,传统计算机的发展似乎面临了瓶颈。在这样的背…...

.Net平台下OpenGL绘制图形(1)(VS2019,Winform,C#)
1、介绍 OpenGL(英语:Open Graphics Library,译名:开放图形库或者“开放式图形库”)是用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口(API)。这个接口由近350个不同的函数调用组成…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
