运算符重载函数作为类的成员函数——有理数的约分
目录
一、题目
二、代码
三、算法分析
(一)数学表达式
(二) 代码实现
一)+运算符重载函数
二)优化函数(实现有理数约分)
一、题目
通过运算符重载为类的成员函数来实现两个有理数对象的加减乘除运算;
有理数是一个可以化为分数的数,如2/3,533/920,都是有理数,而根号2、Π等就为无理数。
在C++中,并没有预先定义有理数,需要时可以声明一个有理数类,将有理数的分子和分母分别存放在nume和deno变量中,对有理数的各种操作都可以用重载运算符来实现。可以写一个优化函数optimize,它的作用时使有理数约去公分母,也就是说,使保存的有理数分子和分母之间没有公约数(除1以外)。在创建有理数对象时才能执行它,在执行各种运算之后也能执行它,从而保证所存储的有理数都是最优的。
二、代码
#include<iostream>
using namespace std;
#include<cmath>class Rational //定义有理数类
{public:Rational(int x=0,int y=1); //类的构造函数void print(); //打印出有理数Rational operator+(Rational a); //类的运算符重载函数(成员函数),实现有理数加法private:int nume; //分子int deno; //分母void optimize(); //优化函数,实现对有理数的约分
};
void Rational::optimize() //优化函数,实现对有理数的约分
{int gcd,i; //gcd存放分子和分母较大的一个,i记录更新的公约数if(nume==0) //①如果分子为0,则分母置1,返回,约分结束{deno=1;return;}//②分子不为0,继续约分操作gcd=(abs(nume)>abs(deno)?abs(nume):abs(deno)); //gcd为分子和分母中较大的一个if(gcd==0) //若为0,则无需约分,返回,结束约分操作return ;for(i=gcd;i>1;i--) //for循环,从gcd开始,逐次-1,判断是否为公约数,找到一个即返回(最大公约数){if((nume%i==0)&&(deno%i)==0) //判断是否为公约数break;}nume/=i; //根据找到的最大公约数,更新分子和分母deno/=i;if(nume<0&&deno<0) //若分子分母同为负数,则结果为正,所以均改为正{nume=-nume;deno=-deno;}else if(nume<0||deno<0) //若分子分母中有一个为负,则结果为负,分子调整为负,分母调整为正{nume=-abs(nume);deno=abs(deno);}
}
Rational::Rational(int x,int y) //构造函数的定义,同时调用优化函数,对有理数继续约分
{nume=x;deno=y;optimize();
}
void Rational::print() //打印有理数
{cout<<nume;if(nume!=NULL) //①分子不为0cout<<"/"<<deno<<endl;else //②分子为0cout<<endl;
}
//函数返回的不是引用类型,因为不可以作为左值
Rational Rational::operator+(Rational a) //+运算符重载函数,实现类(用户自定义的数据类型)的加法运算
{Rational r; //定义一个临时变量,自动调用类的构造函数,占有栈区,程序结束后系统自动调用析构函数,释放内存r.deno=a.deno*deno;r.nume=a.nume*deno+a.deno*nume;r.optimize(); //运算完也需要约分return r;
}
int main()
{Rational r1(3,14),r2(4,14),r3;r1.print();r2.print();r3=r1+r2;r3.print();return 0;
}
三、算法分析
有理数相加
(一)数学表达式
当两个有理数
和
相加时,可得到这样的算式
分子分母分开存放
分子=a*d+b*c
分母=b*d
运算完毕后,需要对词有理数继续优化,
此操作可通过重载运算符“+”实现。
(二) 代码实现
一)+运算符重载函数
代码
Rational Rational::operator+(Rational a) //+运算符重载函数,实现类(用户自定义的数据类型)的加法运算
{
Rational r; //定义一个临时变量,自动调用类的构造函数,占有栈区,程序结束后系统自动调用析构函数,释放内存
r.deno=a.deno*deno;
r.nume=a.nume*deno+a.deno*nume;
r.optimize(); //运算完也需要约分
return r;
}
分析
重载了运算符后,在进行有理数运算时,只需像基本类型的运算一样书写即可,这样给用户带来了很大的方便,并且很直观。
r3=r1+r2;
执行时,C++可以解释为
r3=r1.operator+(r2);
由此可以看出,C++系统在处理算术表达式“r1+r2”时,把对表达式的处理自动转化为对成员运算符重载函数operator+的调用(r1.operator+(r2)),通过“+”运算符左边的对象去调用operator+,“+”右边的对象作为函数调用的实参。
这样双目运算符左边的对象就由系统通过this指针隐含地传递给operator+函数。因此,如果将双目运算符函数重载为类的成员函数,其参数表只需写一个形参就可以了。
但必须要求运算表达式第一个参数(运算符左边的操作数)是一个类对象。而且与运算符函数的返回类型相同。这是因为必须通过类的对象去调用该类的成员函数,而且只要运算符重载函数返回值与改对象同类型,运算才有意义。
二)优化函数(实现有理数约分)
代码
void Rational::optimize() //优化函数,实现对有理数的约分
{
int gcd,i; //gcd存放分子和分母较大的一个,i记录更新的公约数
if(nume==0) //①如果分子为0,则分母置1,返回,约分结束
{
deno=1;
return;
}
//②分子不为0,继续约分操作
gcd=(abs(nume)>abs(deno)?abs(nume):abs(deno)); //gcd为分子和分母中较大的一个
if(gcd==0) //若为0,则无需约分,返回,结束约分操作
return ;
for(i=gcd;i>1;i--) //for循环,从gcd开始,逐次-1,判断是否为公约数,找到一个即返回(最大公约数)
{
if((nume%i==0)&&(deno%i)==0) //判断是否为公约数
break;
}
nume/=i; //根据找到的最大公约数,更新分子和分母
deno/=i;
if(nume<0&&deno<0) //若分子分母同为负数,则结果为正,所以均改为正
{
nume=-nume;
deno=-deno;
}
else if(nume<0||deno<0) //若分子分母中有一个为负,则结果为负,分子调整为负,分母调整为正
{
nume=-abs(nume);
deno=abs(deno);
}
}
分析
寻找最大公约数的步骤
①初始最大公约数gcd
gcd=(abs(nume)>abs(deno)?abs(nume):abs(deno)); //gcd为分子和分母中较大的一个
② 判断是否为公约数
for(i=gcd;i>1;i--) //for循环,从gcd开始,逐次-1,判断是否为公约数,找到一个即返回(最大公约数)
{
if((nume%i==0)&&(deno%i)==0) //判断是否为公约数
break;
}
相关文章:
运算符重载函数作为类的成员函数——有理数的约分
目录 一、题目 二、代码 三、算法分析 (一)数学表达式 (二) 代码实现 一)运算符重载函数 二)优化函数(实现有理数约分) 一、题目 通过运算符重载为类的成员函数来实现两个有…...

mysql数据库的内置函数--7
目录 内置函数 日期函数 字符串函数 数学函数 其它函数 内置函数 在mysql中这些函数用select进行使用 日期函数 函数描述NOW()返回当前的日期和时间CURDATE()返回当前的日期CURTIME()返回当前的时间DATE()从日期或日期/时间表达式中提取日期部分TIME()从日期或日期/时间…...

DS3800HPIB 有效执行任务的所有程序
DS3800HPIB是通用电气公司生产的Speedtronic Mark IV系列的一部分。这DS3800HPIB是一种大型电路板,具有八个连接端子,电路板两侧的尺寸各不相同。左下角有一个红色小方块,上面有一个拨动开关。这DS3800HPIB有大约50个天蓝色的小二极管。这DS3…...

图像比对、人像比对和人脸识别的区别是什么?
图像比对、人像比对和人脸识别都是图像处理技术,但是它们的实现方式和应用场景均有所不同。 图像比对 图像比对是指通过计算机视觉技术将两张或多张图片进行相似度比较。主要包括图像特征提取、匹配和评估等步骤,通常使用神经网络等深度学习技术来实现…...

python中的抽象基类
目录 协议和鸭子类型抽象基类定义抽象基类使用抽象基类直接继承通过注册(register) __subclasshook__魔法方法 协议和鸭子类型 python中有大量的魔法方法,python所谓基于协议编程,就是依赖这些魔法方法。 什么意思呢?…...

耗时几个月,终于决定把原本想用于商业的系统开源了
前言 嗨,大家好,我是希留,一个被迫致力于全栈开发的老菜鸟。 今天又来给小伙伴们分享一个基于 SpringBoot Vue 实现的前后端分离后台管理系统项目; 简介 这个项目是基于xiliu-tenant脚手架项目搭建而成,原本是帮朋…...
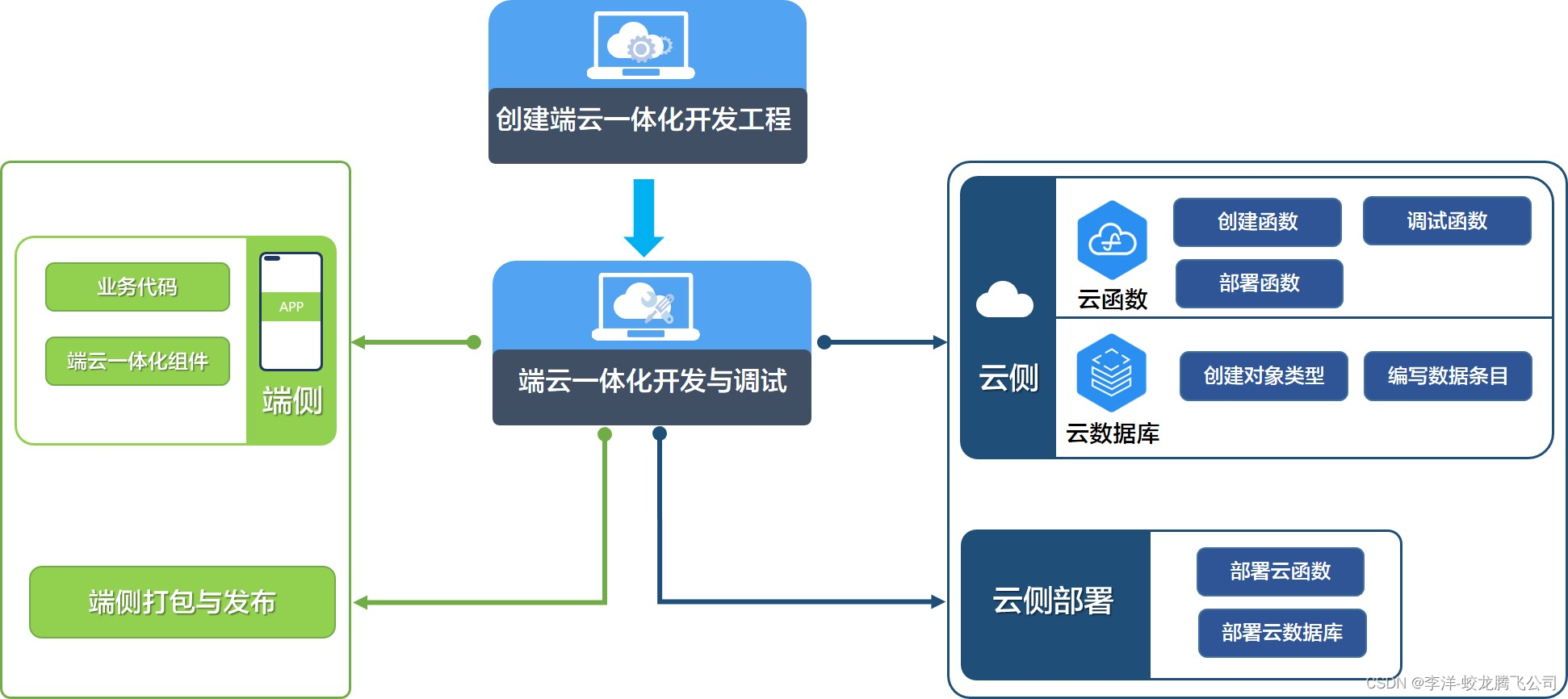
HarmonyOS应用端云一体化开发主要流程
图示 主要步骤 序号 阶段 任务 说明 1 创建端云一体化开发工程 选择工程类型与云开发模板 确定工程类型:选择“Application”或“Atomic Service”页签,确定创建的是HarmonyOS应用工程还是原子化服务工程。选择云开发模板,包括通用云开…...

NoSQL之 Redis配置与优化
NoSQL之 Redis配置与优化 ---------------------- 关系数据库与非关系型数据库 ---------------------------------------- ●关系型数据库: 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一…...

Redis哨兵模式
1.哨兵模式是什么 解释一 哨兵巡查监控 master主机是否故障,如果故障了,根据投票数自动将一个从库转换为新数据库,继续对外服务。 解释二 监控redis 的运行状态,包括master和slave当master宕机后,能自动将slave切换…...
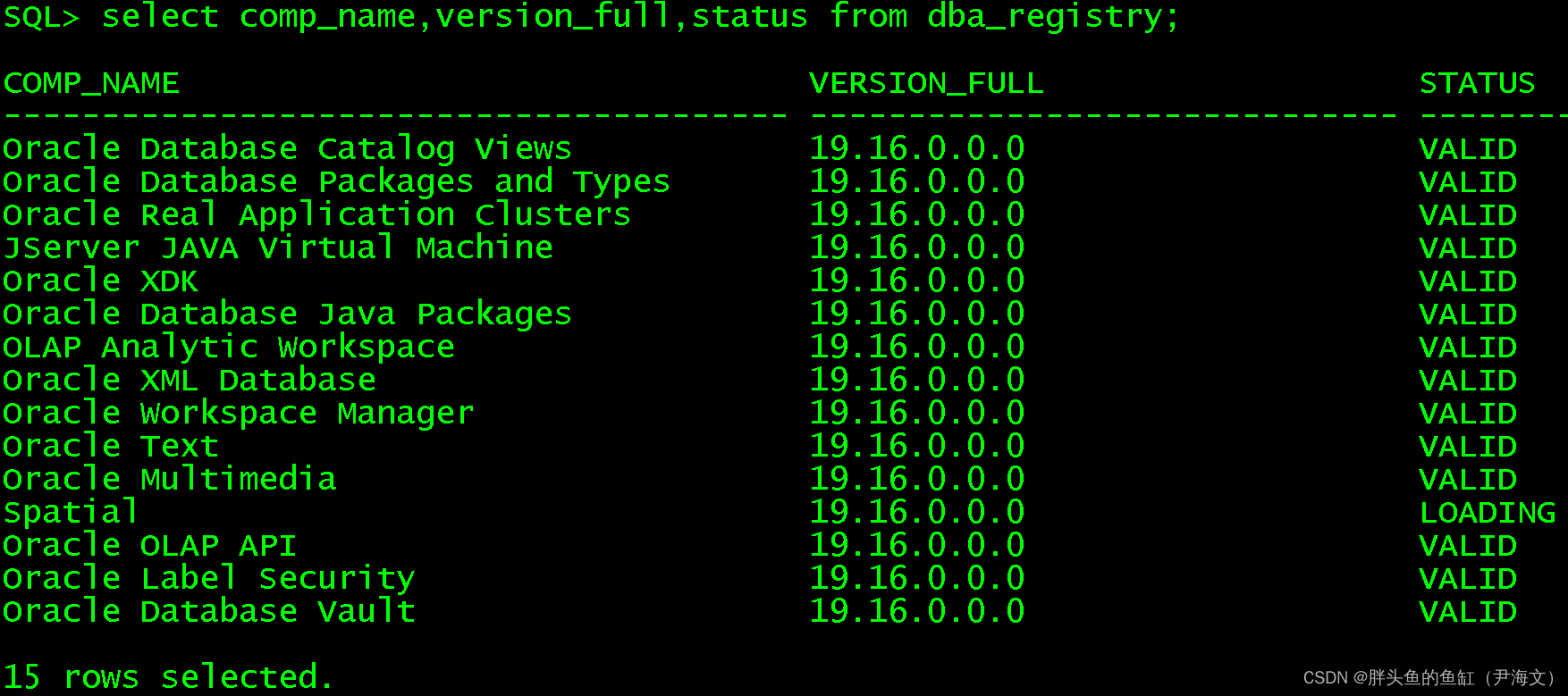
数据库管理-第七十六期 如何升级19c RAC(20230516)
数据库管理 2023-05-16 第七十六期 如何升级19c RAC1 回头处理2 升级AHF3 升级GI及DB3.1 拷贝所需文件3.2 升级OPatch3.3 升级GI与DB3.4 应用SQL变更 4 升级OJVM4.1 解压补丁4.2执行补丁冲突检查:4.3 升级OJVM4.4 应用SQL变更 5 最终验证总结 第七十六期 如何升级19…...
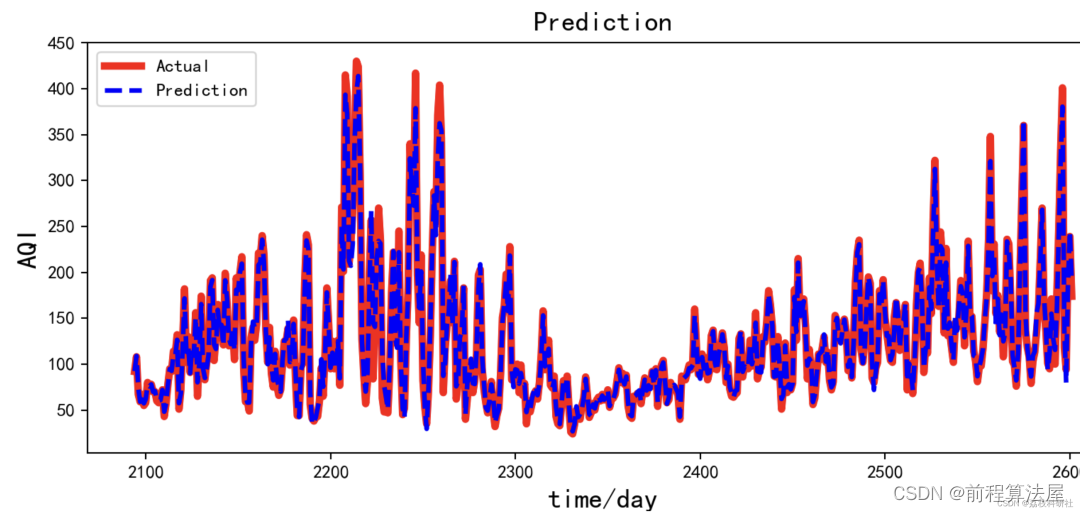
组合预测模型 | ARIMA-CNN-LSTM时间序列预测(Python)
组合预测模型 | ARIMA-CNN-LSTM时间序列预测(Python) 目录 组合预测模型 | ARIMA-CNN-LSTM时间序列预测(Python)预测结果基本介绍程序设计参考资料 预测结果 基本介绍 ARIMA-CNN-LSTM是一种结合了传统时间序列模型和深度学习模型的…...
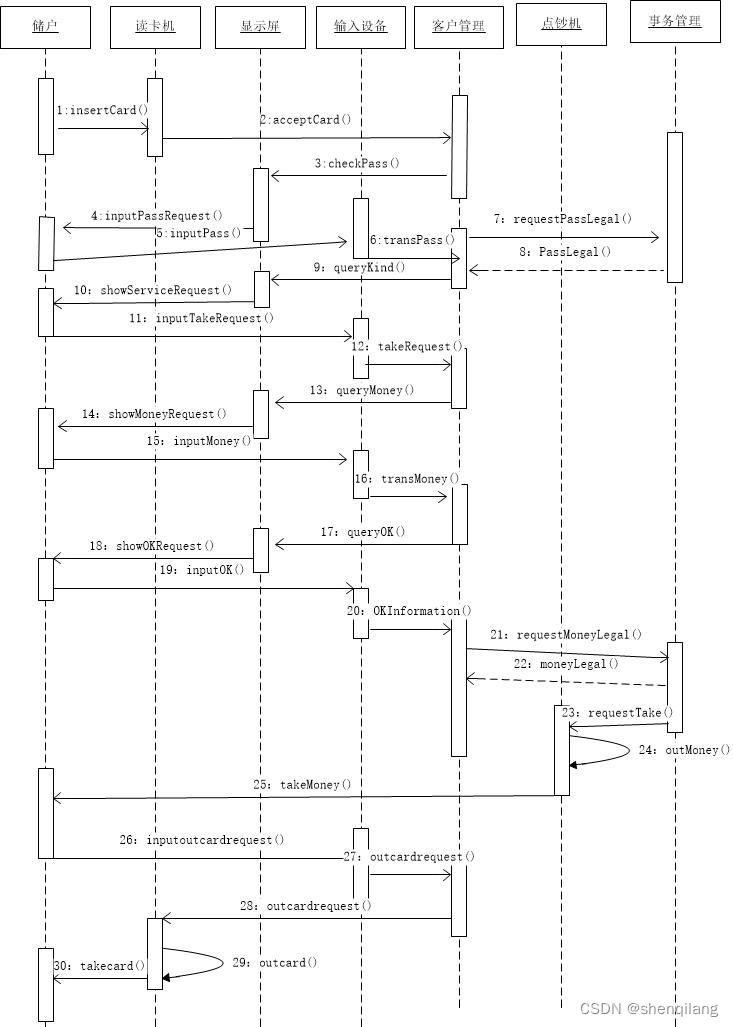
实验四 面向对象分析与设计——UML类图与时序图
一、实验目的: 掌握面向对象分析中静态结构模型与动态行为模型的基本思想。学会识别系统中的类、类的属性和操作以及类之间的关系,掌握UML类图的绘制方法。了解时序图的作用和组成元素,掌握UML时序图的绘制方法。 二、实验仪器及实验环境&a…...
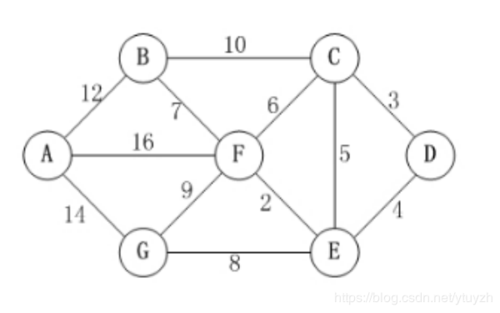
最短路径问题
如图,设定源点为D,终点为A,则D到A的最短路径是多少? 算法思路: 第一步,从源点D出发,此时能到达的选择是C和E,我们根据路径长度选择最少的作为下一个节点,于是选择C&…...

国内有哪些SAAS软件?SAAS软件有哪些优点?
国内有哪些SAAS软件?SAAS软件有哪些优点?不请自来答一下,通过SaaS软件与传统软件的对比来详细讲下SaaS软件有哪些优点? 配合以下内容食用更佳: 关于概念——深度详解什么是SaaS(软件即服务)关…...

分享两组不同的3D VR卡片
最近某音上出现了很多VR视频,转动手机可以看到手机界面未显示出来的场景。这种事情我觉得我们也可以做到。 所以两种不同的3D VR卡片来了: 第一种是横向或上下可以拖动极大的距离。卡片上的信息会随着拖动移动,但不会显示更多的信息&#x…...
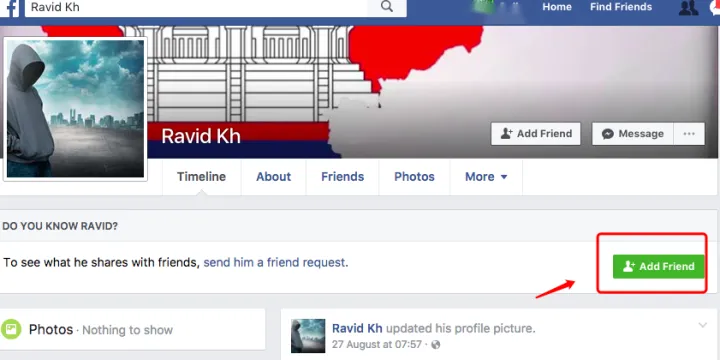
外贸人如何精准开发客户?Facebook开发客户全攻略
现在做跨境的都了解的一个社媒平台就是Facebook了,因为很多人都会拿Facebook来开发客户,忙里偷闲,今天东哥就来聊聊用Facebook开发客户的一些心得。 用Facebook开发客户的心得 1、利用关键词搜索 使用行业相关的关键词、产品特定的关键词、相…...

一、Git安装(Git+TortoiseGit图形化)
Git 是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。 Git 是 Linus Torvalds 为了帮助管理 Linux 内核开发而开发的一个开放源码的版本控制软件。 Git 与常用的版本控制工具 CVS, Subversion 等不同,它采用了分布式版本库的方式…...

mysql死锁,如何产生?如何发现?如何处理?
1 产生死锁 就是资源互斥 例子如下 好的,请参考以下 SQL 语句来创建 base_account_item 表和向表中插入一些数据: CREATE TABLE base_account_item (id INT(11) NOT NULL,account_item_name VARCHAR(50) NOT NULL,PRIMARY KEY (id) ) ENGINEInnoDB DEF…...
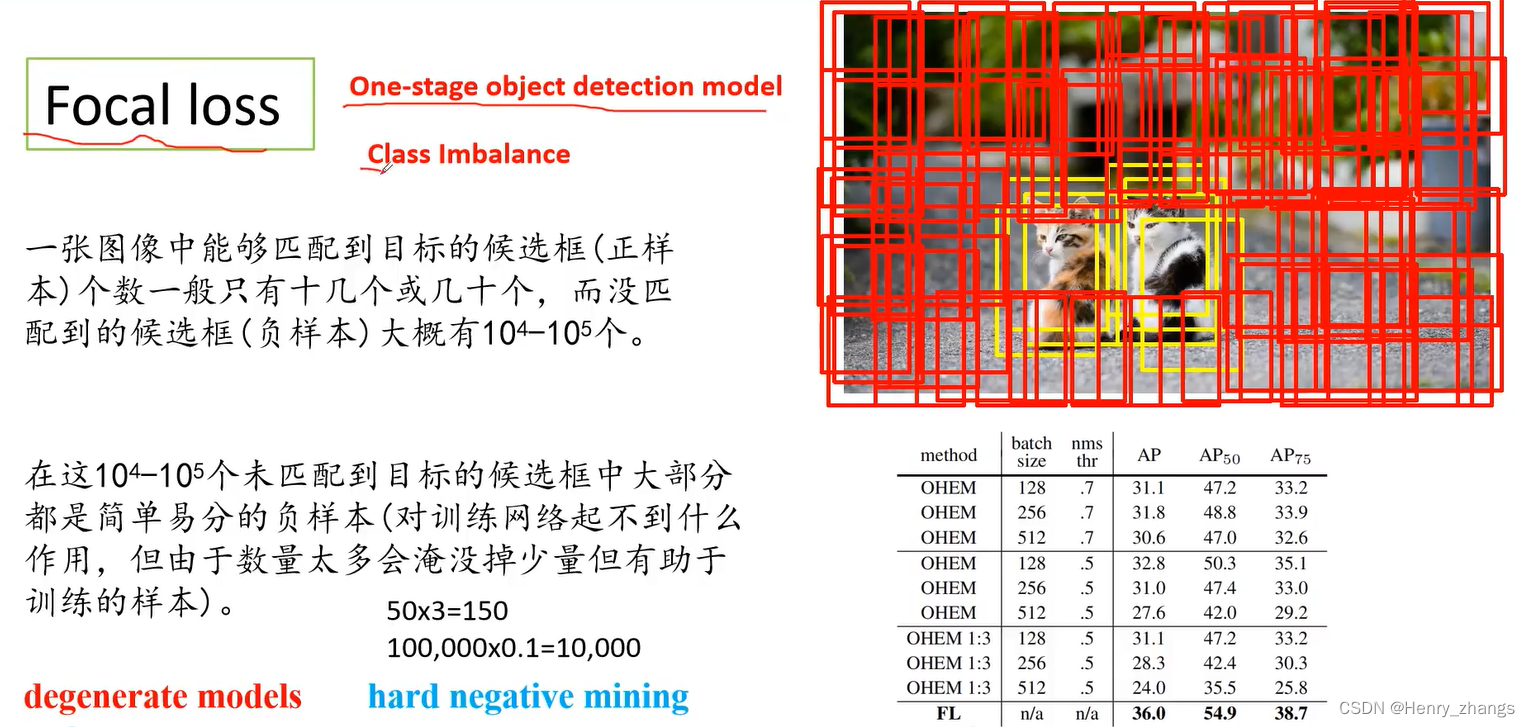
YOLO V1-V3 简单介绍
目录 1. YOLO 2. YOLO V1 3. YOLO V2 4. YOLO V3 5. YOLO V3 SPP网络 5.1 Mosaic 图像增强 5.2 SPP 模块 5.3 CIou Loss 5.4 Focal loss 1. YOLO YOLO 是目标检测任务强大的算法,将目标检测的问题转换边界框和相关概率的回归问题,是目标检测…...
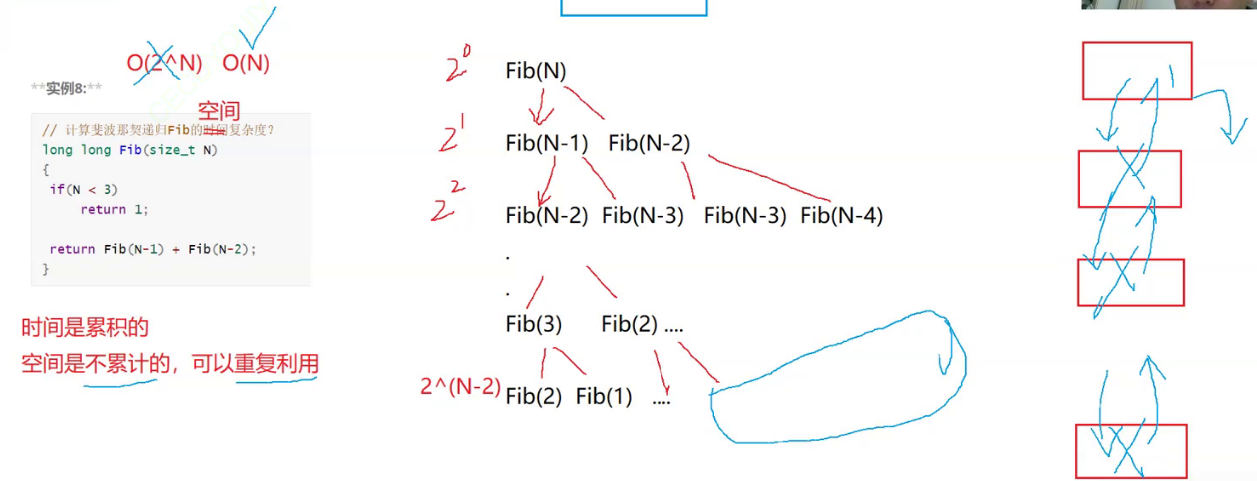
数据结构总结1:了解数据结构、时间复杂度、空间复杂度
后续可能会有补充和更改 目录 一、数据结构 1.算法介绍 二、时间复杂度、空间复杂度 三、练习 1.时间复杂度 2.空间复杂度 一、数据结构 数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。 数据结构和数据库的区…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
