最短路径问题
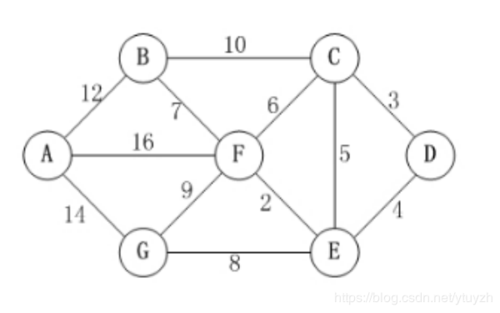
如图,设定源点为D,终点为A,则D到A的最短路径是多少?
算法思路:
第一步,从源点D出发,此时能到达的选择是C和E,我们根据路径长度选择最少的作为下一个节点,于是选择C,
第二步,到达C后,标记C已经走过了,后续再做选择时,排除C。然后将所有C能到达的节点告知D,也就是B、F、E。由D来分辨,B、F、E这些点,是通过C节点路最短,还是D现有方案最短。选择最短的方案记录下来。然后选择B、F、E中C节点最近的、没标记过的节点作为下一步。
第三步,重复第二步操作,直到选不到下一个节点而结束。
考虑特殊的情况,假如图不是闭环的,这个方式可能会被引导在断路的地方停止。于是记录走过的路,当找不到路的时候,确认end没有找到,且还有节点没被标记的情况下,退回上一个路口。
(1)如果节点都被标记或者已经找到终点了,就退出
(2)如果还有节点未被标记可以回退上一次选择的地方继续选择。
最后直接询问源节点D中对于终点A的方案是什么,最短路径是多少。
代码:
封装图中的节点
class Node {String name;//当前节点名称Map<String, Integer> path = new HashMap<>();//目标节点->最短路径public Node(String name) { this.name = name; }/*** 更新到达某个节点的最短路径* @param name 目标节点* @param len 最短路径*/public void update(String name, int len) {path.put(name, len);}/*** 获取指定节点的最短路径* @param name 目标节点* @return 最短路径*/public int getLen(String name) {return path.getOrDefault(name, Integer.MAX_VALUE);}}用到全局变量存储信息,方法里传递这些也行,就是不好看
Map<String, Node> map = new HashMap<>();//节点对象map
Map<String, Boolean> sign = new HashMap<>();//节点标记
List<String> list = new ArrayList<>();//记录走的路径,处理碰到死路的情况,可以退上一个节点初始化代码,将图上的数据跑入节点对象中。
Object[][] params = {{"A", "B", 12},{"A", "F", 16},{"A", "G", 14},{"B", "F", 7},{"B", "C", 10},{"C", "F", 6},{"C", "E", 5},{"C", "D", 3},{"D", "E", 4},{"E", "F", 2},{"E", "G", 8},{"F", "G", 9}
};
//导入路径数据
for(Object[] p:params){if(!map.containsKey((String)p[0]))map.put((String)p[0],new Node((String) p[0]));if(!map.containsKey((String)p[1]))map.put((String)p[1],new Node((String) p[1]));map.get((String)p[0]).update((String)p[1],(int)p[2]);map.get((String)p[1]).update((String)p[0],(int)p[2]);
}开始算法
/*** 选择它下面最小路径出发,更新自己到达最近节点位置** @param name*/boolean f(String name, Node start, String end) {Node now = map.get(name);//获取节点实体sign.put(name, true);//标记已经走过了list.add(name);/*** 更新源节点对能到达节点的最短路径,当前节点是源节点的时候不用更新*/if (!name.equals(start.name)) {int nowLen = start.getLen(name);//取出源节点到当前节点的最短路径,用于后续计算for (String key : now.path.keySet()) {//取出当前节点能直达的所有节点if (!key.equals(start.name)) {//将当前节点到达每一个节点的路径信息告知给到源节点,让源节点扩充自己的最短路径数据int newNodeLen = now.getLen(key) + nowLen;//源节点到新节点的路径长度if (start.getLen(key) > newNodeLen) { //源节点取出原有方案,对比,保留最短的方案start.update(key, newNodeLen);map.get(key).update(start.name, newNodeLen);//路径双方都更新}}}}String nextName = getNextName(now,end);if (nextName == null) return true;return f(nextName, start, end);}里面涉及到选择最近节点的方法以及包含死路的时候回退操作,
/*** 获取下一个路径节点* @param now* @param end* @return*/public static String getNextName(Node now,String end){String nextName = null;int min = Integer.MAX_VALUE;for (String key : now.path.keySet()) {if (sign.containsKey(key) && sign.get(key)) continue;if (now.getLen(key) < min) {min = now.getLen(key);nextName = key;}}if (nextName == null) {if (sign.containsKey(end) && sign.get(end)) return null;}else{return nextName;}list.remove(list.size()-1);return getNextName(map.get(list.get(list.size()-1)),end);}最后使用上面这些东西
String start="D";//源节点
String end="A";//目标节点
f(start, map.get(start), end);
System.out.println(map.get(start).getLen(end));无脑完整代码:
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;public class Main {public static Map<String, Node> map = new HashMap<>();//节点信息public static Map<String, Boolean> sign = new HashMap<>();//防止重复计算public static List<String> list = new ArrayList<>();//记录走的路径,处理碰到死路的情况,可以退上一个节点public static void main(String[] args) {init();//初始化数据String start = "D";//源节点String end = "A";//目标节点f(start, map.get(start), end);//算法寻找System.out.println(map.get(start).getLen(end));//拿出来始终节点的最短路径}/*** 初始化数据*/public static void init(){Object[][] params = {{"A", "B", 12},{"A", "F", 16},{"A", "G", 14},{"B", "F", 7},{"B", "C", 10},{"C", "F", 6},{"C", "E", 5},{"C", "D", 3},{"D", "E", 4},{"E", "F", 2},{"E", "G", 8},{"F", "G", 9}};//导入路径数据for (Object[] p : params) {if (!map.containsKey((String) p[0])) map.put((String) p[0], new Node((String) p[0]));if (!map.containsKey((String) p[1])) map.put((String) p[1], new Node((String) p[1]));map.get((String) p[0]).update((String) p[1], (int) p[2]);map.get((String) p[1]).update((String) p[0], (int) p[2]);}}/*** 选择它下面最小路径出发,更新自己到达最近节点位置** @param name*/public static boolean f(String name, Node start, String end) {Node now = map.get(name);//获取节点实体sign.put(name, true);//标记已经走过了list.add(name);/*** 更新源节点对能到达节点的最短路径,当前节点是源节点的时候不用更新*/if (!name.equals(start.name)) {int nowLen = start.getLen(name);//取出源节点到当前节点的最短路径,用于后续计算for (String key : now.path.keySet()) {//取出当前节点能直达的所有节点if (!key.equals(start.name)) {//将当前节点到达每一个节点的路径信息告知给到源节点,让源节点扩充自己的最短路径数据int newNodeLen = now.getLen(key) + nowLen;//源节点到新节点的路径长度if (start.getLen(key) > newNodeLen) { //源节点取出原有方案,对比,保留最短的方案start.update(key, newNodeLen);map.get(key).update(start.name, newNodeLen);//路径双方都更新}}}}String nextName = getNextName(now,end);if (nextName == null) return true;return f(nextName, start, end);}/*** 获取下一个路径节点* @param now* @param end* @return*/public static String getNextName(Node now,String end){String nextName = null;int min = Integer.MAX_VALUE;for (String key : now.path.keySet()) {if (sign.containsKey(key) && sign.get(key)) continue;if (now.getLen(key) < min) {min = now.getLen(key);nextName = key;}}if (nextName == null) {if (sign.containsKey(end) && sign.get(end)) return null;}else{return nextName;}list.remove(list.size()-1);return getNextName(map.get(list.get(list.size()-1)),end);}
}
class Node {String name;//当前节点名称Map<String, Integer> path = new HashMap<>();//目标节点->最短路径public Node(String name) {this.name = name;}/*** 更新到达某个节点的最短路径** @param name 目标节点* @param len 最短路径*/public void update(String name, int len) {path.put(name, len);}/*** 获取指定节点的最短路径** @param name 目标节点* @return 最短路径*/public int getLen(String name) {return path.getOrDefault(name, Integer.MAX_VALUE);}
}相关文章:

最短路径问题
如图,设定源点为D,终点为A,则D到A的最短路径是多少? 算法思路: 第一步,从源点D出发,此时能到达的选择是C和E,我们根据路径长度选择最少的作为下一个节点,于是选择C&…...

国内有哪些SAAS软件?SAAS软件有哪些优点?
国内有哪些SAAS软件?SAAS软件有哪些优点?不请自来答一下,通过SaaS软件与传统软件的对比来详细讲下SaaS软件有哪些优点? 配合以下内容食用更佳: 关于概念——深度详解什么是SaaS(软件即服务)关…...

分享两组不同的3D VR卡片
最近某音上出现了很多VR视频,转动手机可以看到手机界面未显示出来的场景。这种事情我觉得我们也可以做到。 所以两种不同的3D VR卡片来了: 第一种是横向或上下可以拖动极大的距离。卡片上的信息会随着拖动移动,但不会显示更多的信息&#x…...
外贸人如何精准开发客户?Facebook开发客户全攻略
现在做跨境的都了解的一个社媒平台就是Facebook了,因为很多人都会拿Facebook来开发客户,忙里偷闲,今天东哥就来聊聊用Facebook开发客户的一些心得。 用Facebook开发客户的心得 1、利用关键词搜索 使用行业相关的关键词、产品特定的关键词、相…...

一、Git安装(Git+TortoiseGit图形化)
Git 是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。 Git 是 Linus Torvalds 为了帮助管理 Linux 内核开发而开发的一个开放源码的版本控制软件。 Git 与常用的版本控制工具 CVS, Subversion 等不同,它采用了分布式版本库的方式…...

mysql死锁,如何产生?如何发现?如何处理?
1 产生死锁 就是资源互斥 例子如下 好的,请参考以下 SQL 语句来创建 base_account_item 表和向表中插入一些数据: CREATE TABLE base_account_item (id INT(11) NOT NULL,account_item_name VARCHAR(50) NOT NULL,PRIMARY KEY (id) ) ENGINEInnoDB DEF…...
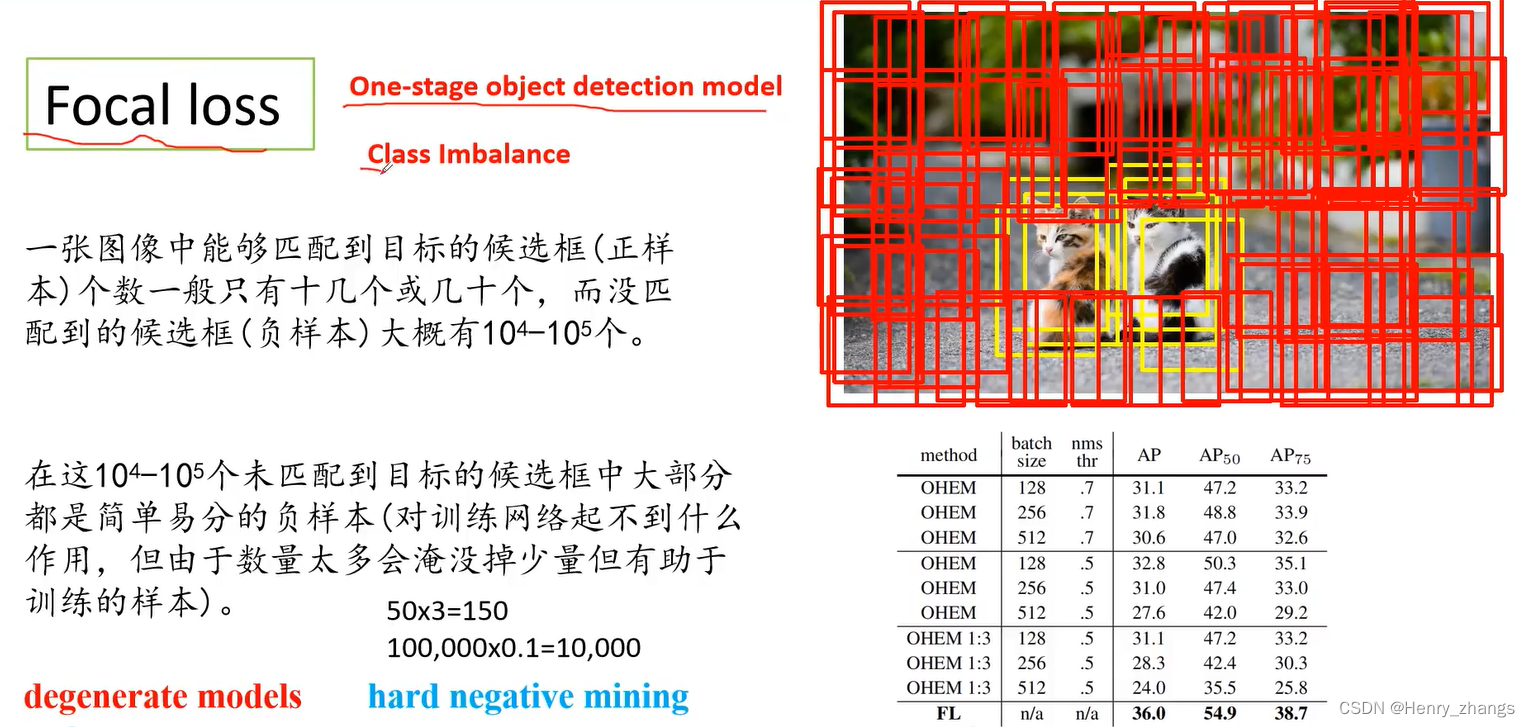
YOLO V1-V3 简单介绍
目录 1. YOLO 2. YOLO V1 3. YOLO V2 4. YOLO V3 5. YOLO V3 SPP网络 5.1 Mosaic 图像增强 5.2 SPP 模块 5.3 CIou Loss 5.4 Focal loss 1. YOLO YOLO 是目标检测任务强大的算法,将目标检测的问题转换边界框和相关概率的回归问题,是目标检测…...
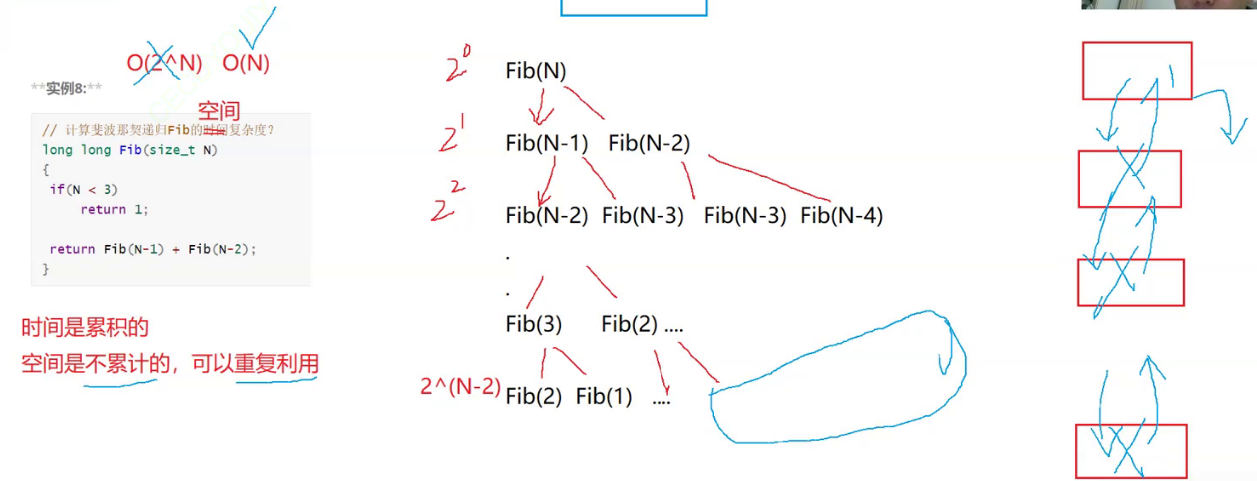
数据结构总结1:了解数据结构、时间复杂度、空间复杂度
后续可能会有补充和更改 目录 一、数据结构 1.算法介绍 二、时间复杂度、空间复杂度 三、练习 1.时间复杂度 2.空间复杂度 一、数据结构 数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。 数据结构和数据库的区…...

abstract class和interface有什么区别?
含有abstract修饰符的class即为抽象类,abstract 类不能创建的实例对象。含有abstract方法的类必须定义为abstract class,abstract class类中的方法不必是抽象的。abstract class类中定义抽象方法必须在具体(Concrete)子类中实现,所以…...
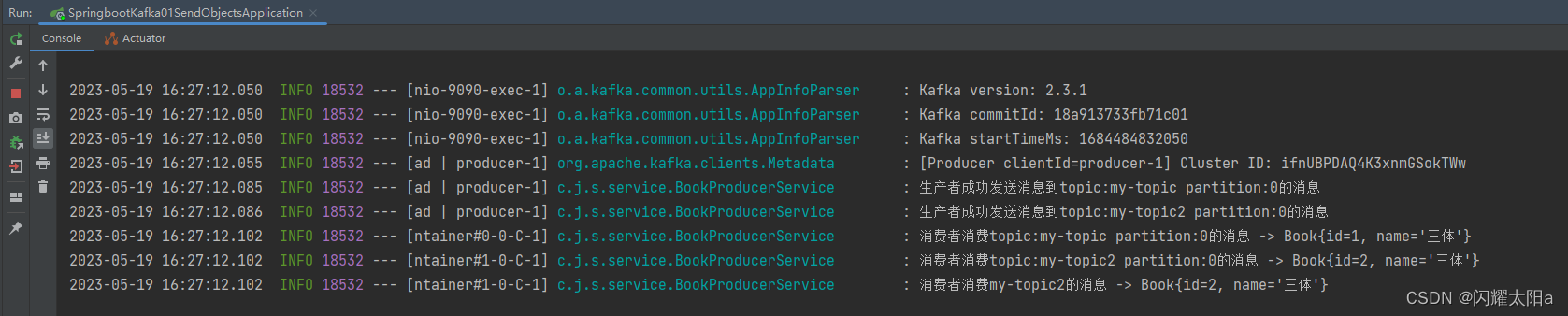
Kafka在Java项目中的应用
Kafka在Java项目中的应用 Docker 安装Kafka 一.首先需要安装docker,可看这篇文章安装docker 二.拉取zookeeper和KafKa镜像 docker pull wurstmeister/zookeeperdocker pull wurstmeister/kafkaKafka组件需要向zookeeper进行注册,所以也需要安装zookeeper 三.启动zookeeper…...

理解分布式id生成算法SnowFlake
理解分布式id生成算法SnowFlake 分布式id生成算法的有很多种,Twitter的SnowFlake就是其中经典的一种。 概述 SnowFlake算法生成id的结果是一个64bit大小的整数,它的结构如下图: } public function __construct(){ $this->rnew…...
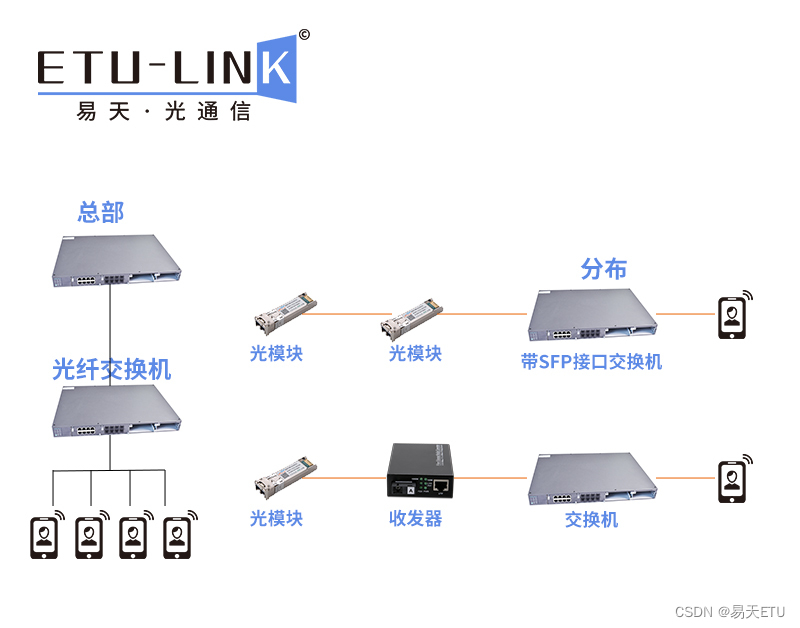
光纤收发器可以连接光模块吗?
随着科技的进步发展,城市信息化速度的加快,光通信产品在数据中心和安防监控等场景中的运用越来越广泛,而这之间的连接则需要光模块和光纤收发器来实现。很多用户对光模块和光纤收发器的使用有些疑虑,两者该如何连接?又…...
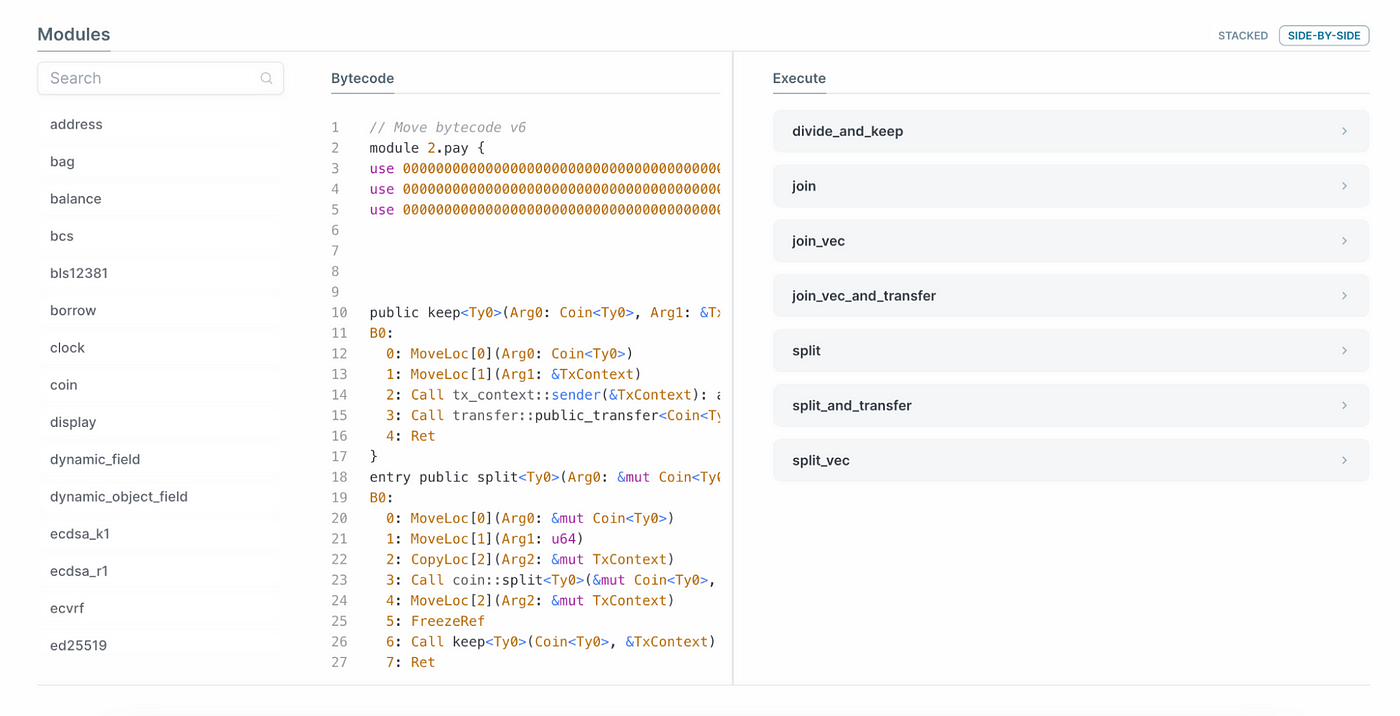
一文快速了解浏览器Sui Explorer
Sui作为一条基于第一原理重新设计和构建而成的L1公链,所有区块和交易信息皆公开透明,每个人都能自行查看。通过Sui链上浏览器,用户可以迅速了解链上的交易情况,比如当前的TPS和Gas价格,也可以使用Digest来查看特定交易…...

python中lambda、yield、map、filter、reduce的使用
1、 匿名函数lambda python中允许使用lambda关键字定义一个匿名函数。所谓的匿名函数就是说使用一次或者几次之后就不再需要的函数,属于“一次性”函数。 #例1:求两数之和 f lambda x, y: x y print(f(5, 1))#例2:求平方和 print((lambda…...

第十八章 使用LNMP架构部署动态网站环境
文章目录 第十八章 使用LNMP架构部署动态网站环境一、源码包程序1、源码包的优势2、基本步骤(1)、下载及解压源码包文件(2)、编译源码包代码(3)、生成二进制安装程序(4)、运行二进制…...
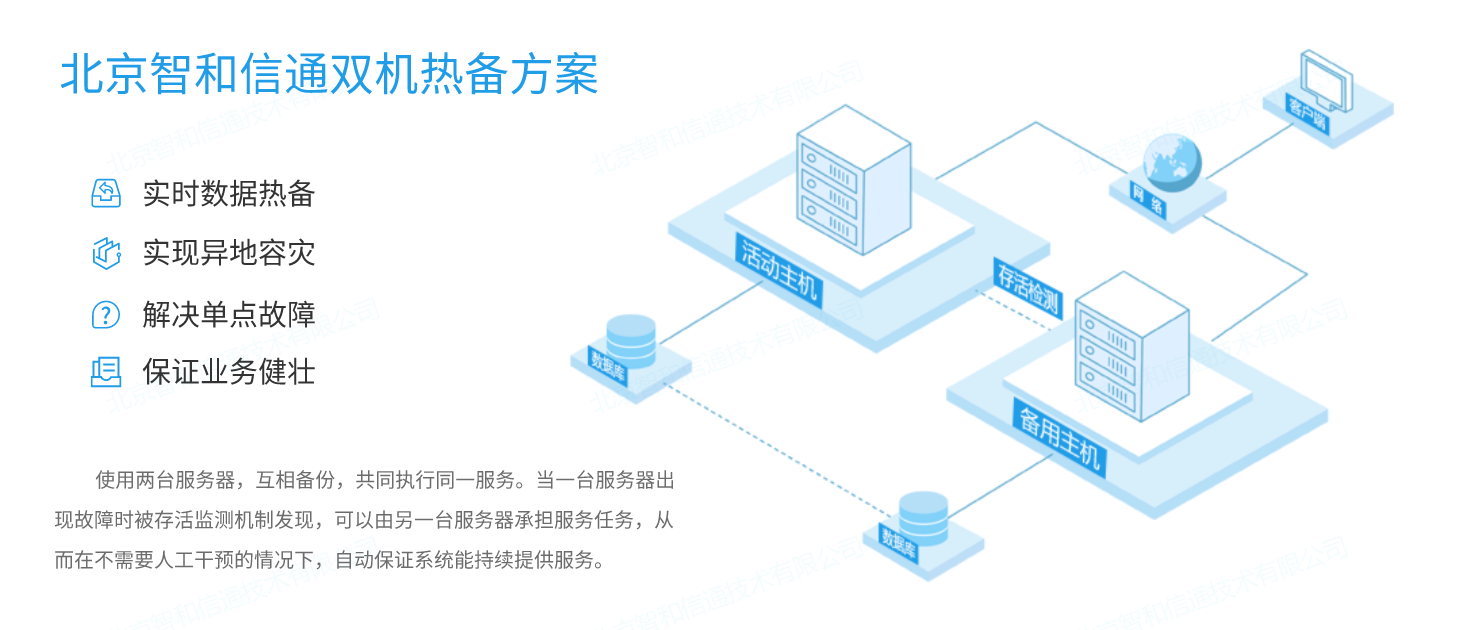
无人值守的IDC机房动环综合运维方案
企业数字化转型以及5G、物联网、云计算、人工智能等新业态带动了数据中心的发展,在国家一体化大数据中心及“东数西算”节点布局的推动下,数据中心机房已成为各大企事业单位维持业务正常运营的重要组成部分,网络设备、系统、业务应用数量与日…...
桌面远程工具推荐
目前市面上的远程工具多如牛毛,很多人不知道怎么选择,下面小编介绍两种桌面远程工具,它们都是跨平台的,均支持Windows,Mac OS,IOS和安卓,分别是RayLink,VNC,好用…...
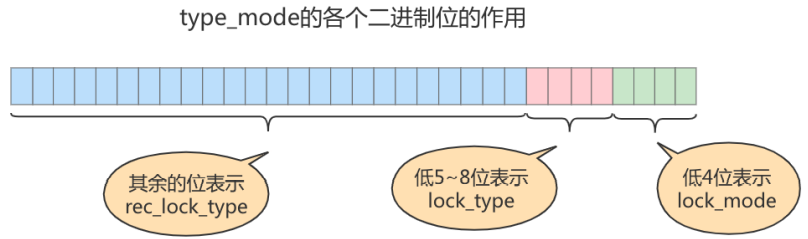
MySQL高级——第15章_锁
第15章_锁 1. 概述 锁是计算机协调多个进程或线程并发访问某一资源的机制。在程序开发中会存在多线程同步的问题,当多个线程并发访问某个数据的时候,尤其是针对一-些敏感的数据(比如订单、金额等),我们就需要保证这个数据在任何 时刻最多只…...
【ROS】Ubuntu22.04安装ROS2(Humble Hawksbill)
0、版本说明 Ubuntu22.04对应的ROS2的版本为Humble Hawksbill(ros-humble) 如果不是在Ubuntu22.04中安装ROS,请参考下面Ubuntu和ROS的版本对应关系 1、更新apt包列表 $ sudo apt update2、设置编码 将ubuntu环境语言编码设置为en_US en_…...
【ChatGPT】体验一下ChatGPT
体验一下ChatGPT 可以帮你写代码、写邮件、编故事的神器 最近OpenAI 发布了备受期待的原型通用 ChatGPT,这是一种基于对话的 AI 聊天界面,算是GPT-3(Generative Pre-trained Transformer 3)的继承者,今天记录一下体验的过程,以前…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
