小程序容器助力智能移动门户统一
智能移动统一门户遵循“统一规划,统一标准,统一建设,统一运维”的指导思想。它灵活运用前端展示平台,微服务后端平台,流程引擎,规则引擎,非结构化数据平台,即时通讯平台,无纸化平台和统一认证平台等基本平台工具来开放我们的生产作业。
统一门户的发展可以追溯到20世纪90年代初期,当时的企业和组织开始意识到信息技术可以用于整合和管理各种分散的应用程序和服务。随着互联网的普及和Web 2.0技术的兴起,统一门户的发展迅速加速。
在早期,统一门户主要采用定制化开发的方式实现,即通过编写自定义代码和脚本,将各种应用程序和服务整合到一个统一的Web界面中。这种方式虽然可以实现高度的定制化和集成化,但开发周期长、成本高、维护难度大。
随着开源技术和标准化协议的发展,统一门户开始采用基于开源平台和标准化协议的方式实现。例如,采用Liferay、Drupal、WordPress等开源平台,通过Web Services、RESTful API、OAuth等协议实现各种应用程序和服务的集成。这种方式具有开发周期短、成本低、维护简便、扩展性好等优点。

统一门户的必要性和价值
通俗易懂的说,统一门户是指一个集成了多种应用程序和服务的单一入口网站。它可以让用户通过一个登录认证界面,访问到他们所需要的各种信息资源、工具和应用程序,而无需再次进行身份验证或切换到其他应用程序。
统一门户通常是为了解决企业或组织内部的信息孤岛问题而创建的。许多组织拥有许多不同的应用程序和服务,这些应用程序和服务通常都有各自独立的登录认证和用户界面。这种分散的信息和服务对于用户来说可能很不方便,也会导致信息孤岛的问题。
一些常见的对外统一门户:
-
政府门户:许多国家和地区的政府都提供了对外的门户网站,这些网站通常包括政府部门的信息、公共服务、政策法规、数据统计等。例如,中国政府门户网站是www.gov.cn,美国政府门户网站是www.usa.gov。
-
学校门户:许多大学和学院都提供了对外的门户网站,这些网站通常包括学校的招生信息、课程信息、校园新闻、学术研究等。例如,哈佛大学门户网站是www.harvard.edu,北京大学门户网站是www.pku.edu.cn。
-
企业门户:许多企业也提供了对外的门户网站,这些网站通常包括企业的产品信息、服务信息、招聘信息等。例如,苹果公司门户网站是www.apple.com,亚马逊公司门户网站是www.amazon.com。
对于企业来说,对外的统一门户具有很多业务价值,包括以下几个方面:
-
提高客户满意度:企业可以通过门户网站提供的一站式服务,提高客户体验和满意度,从而增加客户忠诚度和业务量。
-
降低运营成本:企业可以通过门户网站提供的自助服务和在线交易,降低人力成本和运营成本,同时提高工作效率。
-
增加销售收入:企业可以通过门户网站提供的在线销售和促销活动,增加销售收入和市场份额。
-
改善信息传播:企业可以通过门户网站提供的新闻、公告和社交媒体,及时传播企业信息和品牌形象,从而提高品牌知名度和美誉度。
-
加强业务管理:企业可以通过门户网站提供的各种管理工具和数据分析,加强业务管理和决策支持,提高企业效益和竞争力。
小程序技术给统一门户的建设带来新的构想
随着小程序技术的发展,统一门户的功能也有了更广阔的想象空间。

先说说小程序生态:自2017年微信小程序正式上线以来,它迅速成为了中国移动互联网行业的一个重要的生态系统。截至2021年底,微信小程序月活跃用户已经超过1.2亿,覆盖了电商、金融、医疗、教育、旅游、出行等各个行业应用场景。微信小程序生态系统也不断完善,为开发者提供了丰富的开发工具、模板和开源组件等资源。
再说说小程序技术:相比于传统的原生应用开发技术,小程序技术具有轻量、快速开发、跨平台、无需安装、更便于用户使用等优势。小程序不需要用户下载安装即可使用,同时小程序的开发成本相对更低,开发速度更快,也更易于维护更新。小程序技术还支持跨平台运行,可以同时在多个移动设备上运行,极大地扩展了应用的覆盖范围,为企业和开发者带来更大的商业价值。市面上一些比较知名的小程序容器技术产品包括:微信、支付宝、百度、抖音小程序等,他们都是以完善大社交平台自有小程序生态的技术底座,能提供第三方进行私有化部署的有:FinClip、mPaaS等产品。据了解,FinClip自行研发的小程序容器技术,能够让企业的App能具备快速运行小程序的能力,他们家的SDK还能嵌入除App以外的职能设备终端中(如 Linux、Windows、MacOS、麒麟等操作系统上运行)。
小程序容器与企业统一门户的建设有很好的结合点,可以实现以下几个方面的结合:
-
提供更多的渠道:通过在小程序容器中发布企业统一门户,可以将企业的服务和内容扩展到更多的移动端用户,提供更便捷的渠道和更好的用户体验。
-
增强互动和用户参与:小程序容器中可以集成多种社交功能,例如朋友圈、评论、点赞等,可以增强用户的参与感和互动性,从而提高用户粘性和忠诚度。
-
实现在线交易和支付:小程序容器集成了微信支付等多种支付方式,可以实现在线交易和支付功能,为企业带来更多的销售机会和营收来源。
-
提供定制化服务:通过小程序容器中的用户数据分析和推荐算法,可以为用户提供更加个性化的服务和推荐,从而增强用户满意度和忠诚度。
-
加强管理和数据分析:小程序容器中集成了多种管理工具和数据分析功能,可以帮助企业实时掌握用户行为、交易数据等关键信息,从而实现更加精细化的管理和决策。
随着移动互联网的快速发展,企业需要更加关注移动端用户的需求和行为,以提供更好的服务和增强用户体验。而小程序容器和企业统一门户的结合,可以为企业带来更多的优势和机会。通过在小程序容器中发布企业统一门户,企业可以扩展更多的移动端渠道,提供更加便捷的服务和增强用户体验;同时,小程序容器也提供了多种社交和支付功能,为企业带来更多的销售机会和营收来源。除此之外,小程序容器还可以帮助企业实现更加个性化的服务和推荐,加强用户互动和参与,并提供更加精细化的管理和决策支持。因此,小程序容器和企业统一门户的结合是企业不可忽视的一部分,可以帮助企业实现更好的移动化服务和发展。
相关文章:

小程序容器助力智能移动门户统一
智能移动统一门户遵循“统一规划,统一标准,统一建设,统一运维”的指导思想。它灵活运用前端展示平台,微服务后端平台,流程引擎,规则引擎,非结构化数据平台,即时通讯平台,…...

opencv-python相机标定详解
文章目录 角点检测查看角点标定 opencv中内置了张正友的棋盘格标定法,通过一些姿态各异的棋盘格图像,就能标定相机的内外参数。 角点检测 第一步是角点检测,首先需要读取棋盘格图像 import numpy as np import cv2 import ospath imgs #…...

由斯坦福、Nautilus Chain等联合主办的 Hackathon 活动,现已接受报名
由 Stanford Blockchain Accelerator、Zebec Protocol、 Nautilus Chain、Rootz Lab 共同主办的黑客松活动,现已接受优秀项目提交参赛申请。 在加密行业发展早期,密码极客们就始终在对区块链世界基础设施,在发展方向的无限可能性进行探索。而…...
)
PBDB Data Service:Measurements of specimens(标本测量)
Measurements of specimens(标本测量) 描述参数以下参数可用于指定您感兴趣的标本种类以下参数可用于筛选所选内容以下参数还可用于根据分类筛选结果列表以下参数可用于生成数据存档您可以使用以下参数选择要检索的额外信息,以及要获取记录的…...
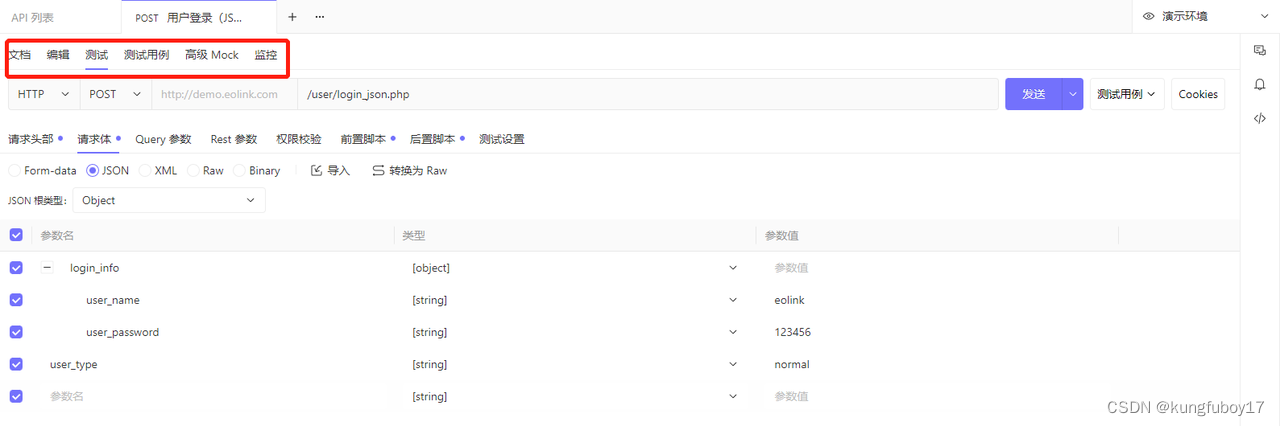
低调的接口工具 ApiKit
最近发现一款接口测试工具--ApiKit,我们很难将它描述为一款接口管理工具 或 接口自测试工具。 官方给了一个简单的说明,更能说明 Apikit 可以做什么。 ApiKit API 管理 Mock 自动化测试 异常监控 团队协作 ApiKit的特点: 接口文档定义&a…...
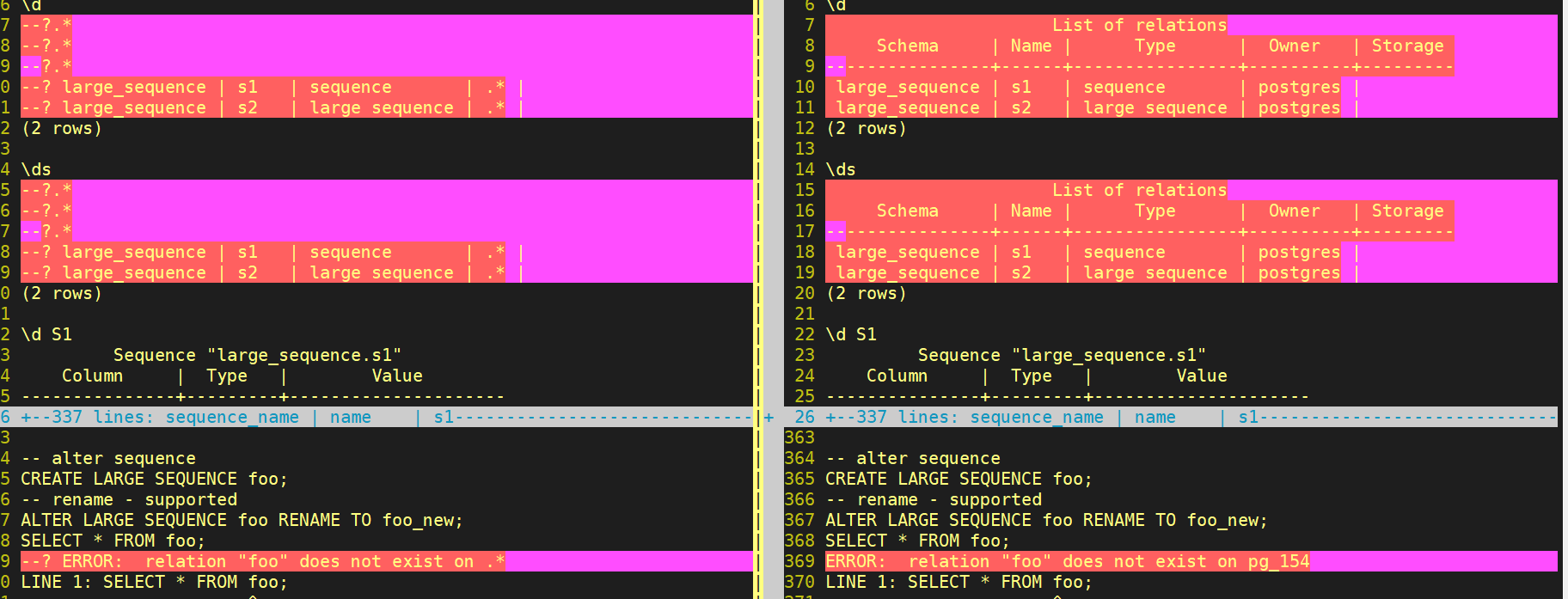
opengauss 的回归测试
目录 一、回归测试说明 二、单独执行测试用例(开发调试) 一、回归测试说明 opengauss/postgresql 的回归测试,通过执行SQL比较输出打印,判断代码修改是否改变了其它功能逻辑。 OG的回归测试大体上和PG类似,主要是通…...

计算机组成原理基础练习题第四章-计算机的运算方法
对真值0表示形式唯一的机器数是()。A、原码 B、补码和移码C、反码 D、以上都不对在整数定点机中,下述说法正确的是()。A、原码和反码不能表示-1,补码可以表示-1B、三种机器数均可表示-1C、三种机器数均可表示…...

SpringBoot定时任务里的多线程
SpringBoot定时任务里的多线程 提示前言遇到的问题验证与解决验证单线程执行单任务分析代码及结果 单线程执行多任务 解决实现单任务的多线程为每个任务创建一个子线程 解决多任务的多线程设定固定容量线程池动态设定容量线程池固定线程池和动态线程池的选择 简单总结借鉴及引用…...

YOLO V3 SPP ultralytics 第二节:根据yolo的数据集,生成准备文件和yolo的配置文件
目录 1. 介绍 2. 完整代码 3. 代码讲解 3.1 生成 my_train_data.txt和my_val_data.txt 3.2 生成 my_data.data 文件 3.3 生成 my_yolov3.cfg 3.4 关于my_data_label.names文件 1. 介绍 根据 第一节 的操作,已经生成了下图中圆圈中的部分,而本…...

camunda流程引擎connector如何使用
在 Camunda 中,Connector 是一种用于与外部系统或服务交互的机制。它允许 BPMN 模型中的 Service Task 节点与外部系统或服务进行通信,从而使流程更加灵活和可扩展。使用 Connector,可以将业务流程与外部系统集成在一起,而无需编写…...

ECO基本概念:pre-mask eco gen patch flow
使用conformal LEC 进行pre-mask eco 时,如何产生patch,参考以下步骤: 官方推荐 Flattened ECO Flow(FEF) Conformal支持Flattened ECO Flow和Hierarchical ECO Flow。Flattened下,工具会将 ECO 分析重点…...
【初学人工智能原理】【4】梯度下降和反向传播:能改(下)
前言 本文教程均来自b站【小白也能听懂的人工智能原理】,感兴趣的可自行到b站观看。 本文【原文】章节来自课程的对白,由于缺少图片可能无法理解,故放到了最后,建议直接看代码(代码放到了前面)。 代码实…...

微信小程序路由传参
微信小程序路由传参 在微信小程序中,可以通过路由传参将数据传递给目标页面。以下是一种常见的方式: 在源页面中,使用 wx.navigateTo 或 wx.redirectTo 方法跳转到目标页面,并通过 URL 参数传递数据。示例: wx.navi…...
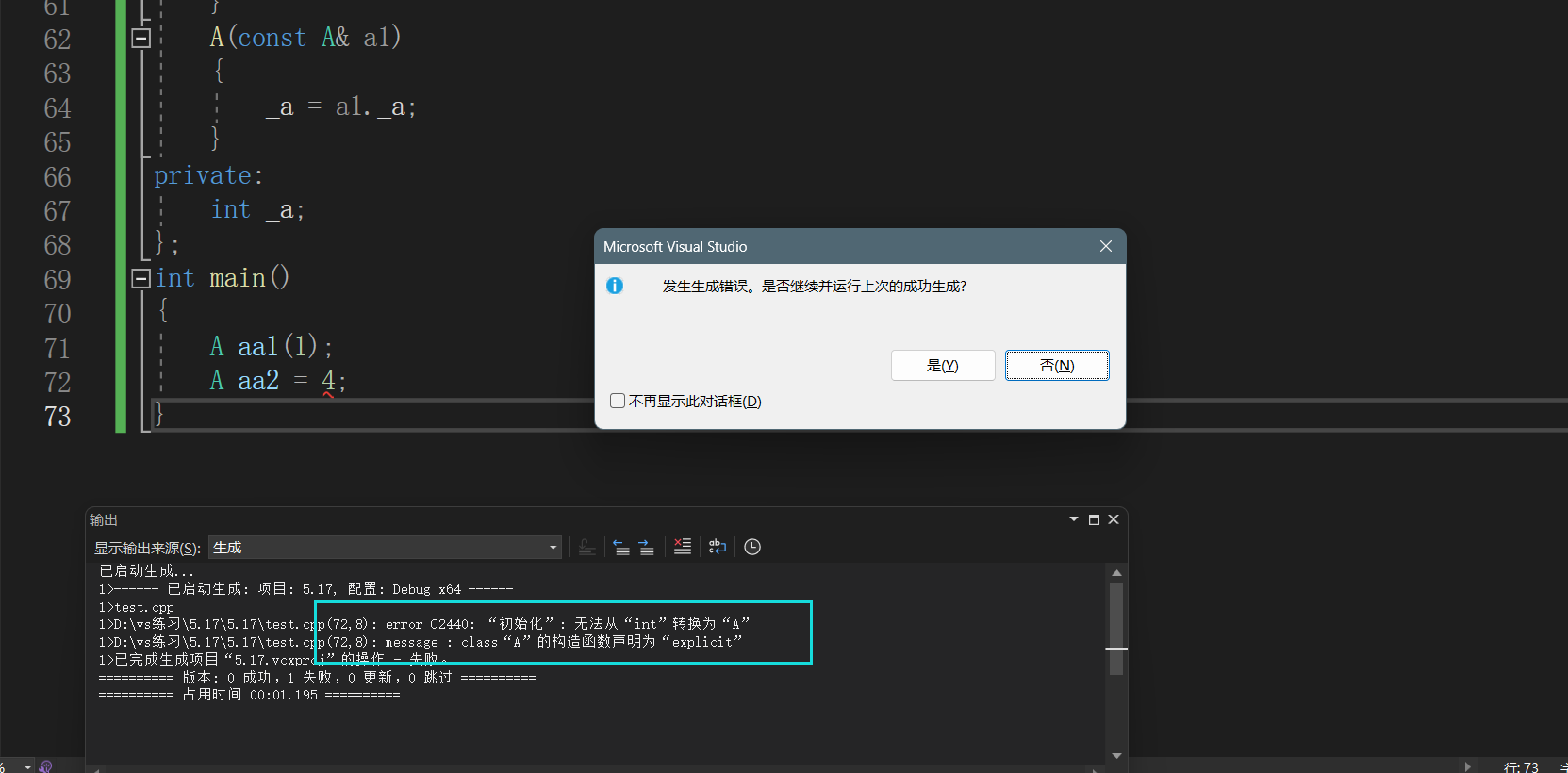
深入篇【C++】类与对象:再谈构造函数之初始化列表与explicit关键字
深入篇【C】类与对象:再谈构造函数之初始化列表与explicit关键字 Ⅰ.再谈构造函数①.构造函数体赋值②.初始化列表赋值【<特性分析>】1.至多性2.特殊成员必在性3.必走性:定义位置4.一致性5.不足性 Ⅱ.explicit关键字①.隐式类型转化②.作用 Ⅰ.再谈…...

广东棒球发展建设·棒球1号位
一、概述 棒球是一项源于美国的运动,自20世纪初开始传入中国,近年来在广东省的发展也逐渐受到关注。本文将就广东棒球的发展现状及未来发展方向进行分析。 二、发展现状 目前广东省内棒球赛事主要有以下几种: 1. 业余棒球联赛:…...

浅谈PMO对组织战略的支持︱美团骑行事业部项目管理中心负责人边国华
美团骑行事业部项目管理中心负责人边国华先生受邀为由PMO评论主办的2023第十二届中国PMO大会演讲嘉宾,演讲议题:浅谈PMO对组织战略的支持。大会将于6月17-18日在北京举办,更多内容请浏览会议日程 议题内容简要: 战略是组织运行的…...

互联网医院资质代办|互联网医院牌照的申请流程
随着互联网技术的不断发展,互联网医疗已经逐渐成为人们关注的热点话题。而互联网医院作为互联网医疗的一种重要形式,也越来越受到社会各界的关注。若想开展互联网医院业务,则需要具备互联网医院牌照。那么互联网医院牌照的申请流程和需要的资…...

网络:DPDK复习相关知识点_2
1.RTC运行至完成时模式,单核单模块 2.pipeline模式,多核多模块,每个模块都是一个处理引擎,但会有缓存一致性问题 3.Mbuff数据包内存操作对象,相当于是数据包的一个索引,对网络的处理都集中在这个Buff上 …...

阿里云大学考试Java中级题目及解析-java中级
阿里云大学考试Java中级题目及解析 1.servlet释放资源的方法是? A.int()方法 B.service()方法 C.close() 方法 D.destroy()方法 D servlet释放资源的方法是destroy() 2.order by与 group by的区别? A.order by用于排序,group by用于排序…...
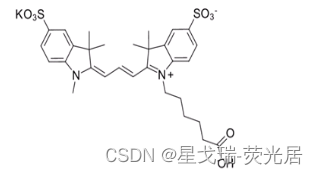
【星戈瑞】Sulfo-CY3-COOH磺化/水溶性Cyanine3羧酸1121756-11-3
Sulfo-CY3 COOH是一种荧光染料,其分子结构中含有COOH官能团,最大吸收波长为550纳米左右,可以通过分光光度计等设备进行检测。Sulfo-CY3 COOH是一种带有羧基的荧光染料,可以与含有氨基的生物分子通过偶联反应形成共价键,…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
