(浙大陈越版)数据结构 第三章 树(上) 3.1 树和树的表示
目录
3.1.1 引子(顺序查找)
什么是树
查找
3.1.2 引子 二分查找例子(BinarySearch)
二分查找
3.1.3 引子 二分查找实现
二分查找代码
二分查找的启示
3.1.4 树的定义
一些基本术语:
3.1.5 树的表示
3.1.1 引子(顺序查找)
什么是树
在客观世界上许多事物存在层次关系。如人类社会的家谱、社会组织管理结构、省市县乡镇的分级,计算机中为了还原这种结构,使用了树这种数据结构。
那么为什么要使用这种层次结构?因为分层组织在数据管理方面有更高的效率
下面以数据管理的基本操作之一:查找为例来分析,如何实现有效的查找?
查找
实质:根据某个给定的关键词K,从集合R中找出与关键词K相同的数据
1. 静态查找
- 定义:集合中的数据是固定的。没有插入和删除,对数据集的操作只有查找。——比如一本出版字典
- 实现:一般使用数组存放数据
- 方法:顺序查找
2. 动态查找
- 定义:集合中数据是动态变化的。对数据集的操作有查找、插入和删除。——比如一个论文数据库
顺序查找详解:(实际上就是遍历)时间复杂度:O(n)
typedef struct LNode *List;
struct LNode{ElementType Element[MaxSize];int length;
};int SequentialSearch(List Tbl,ElementType K)
{//遍历ElementType查找关键字为K的数据元素int i;Tbl->Element[0] = K;//建立哨兵,预先设立边界值而不需要每次都判断for(i = Tbl->Length; Tbl->Element[i] != K; i--);//查找成功返回下标,不成功返回0return i;
}//不用哨兵的
int SequentialSearch(List Tbl,ElementType K)
{int i;//两个退循环条件,i控制边界,tbl检测是否相等for(i = Tbl->Length; i>0 && Tbl->Element[i] != K; i--);return i;
}3.1.2 引子 二分查找例子(BinarySearch)
假设两个地点AB之间的高压电站有100w个,从A向B输电,某一天两个地方都突然停电了,现在需要排查是哪里的电站出问题。如果一个一个排查过去,平均需要50w次才能排查结束。如果先从最中央的一个电站开始排查,再向断电的那一半的中间...每次折半查找,那么只需要log2(1000000)=20次就可以排查完毕。
二分查找
- 前提:数据元素的关键字需要是有序且连续存放
- 退出条件:1.初始时right>left,结束时left>right,二者错位,说明查找失败2.查找成功,返回
3.1.3 引子 二分查找实现
二分查找代码
//函数参数表为存放着数据的列表Tbl和要找的元素K
int BinarySearch(List Tbl, ElementType K)
{//定义左中右标识变量,赋初值,-1为方便返回NoFoundint left,right,mid,NoFound = -1;//初始左右边界,先让左边界为最左侧元素,右边界为表尾left = 1;right = Tbl->length;while(left <= right){mid = (left + right)/2;//若中值大于要找的元素Kif(K < Tbl->Element[mid]){right = mid - 1;//说明应该往左半侧找,把右边界更新为此时的中值-1即可}else if(K > Tbl->Element[mid]){left = mid + 1;}else{return mid;}}//如果找到了会提前退出循环,没找到会返回NoFound即-1return NoFound;
}这个算法的时间复杂度是对数级的O(logN)
二分查找的启示
由二分查找判断元素的顺序可以绘制出如下判定树
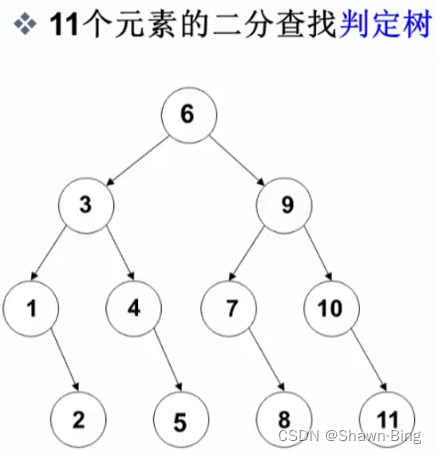
从图中可以发现:
- 每个结点需要查找的次数刚好等于这个结点所在的层数
- 查找次数的上限是这个判定树的深度
- 如果有n个结点,那么判定树的深度为[log2(N)]+1
- 平均查找次数ASL = (每层个数*层数之和)/总结点数。此树ASL = (1+2*2+4*3+4*4)/11=3
那么如果直接将数据存储成树这样的形式,会不会对数据的查找更有裨益呢?当然会。之后我们就将讲到查找树这种存储形式。
3.1.4 树的定义
树(Tree):n(n>=0)个结点构成的有限集合
空树:n=0,即没有结点。其对应的是非空树。
对于任意一颗非空树,它具备以下性质:
树中有一个称为根(Root)的特殊结点,用r表示
其余结点可分为m(m>0)个互不相交的有限集T1、T2、...、Tm,其中每个集合本身也是一棵树,称为原来树的子树(SubTree)
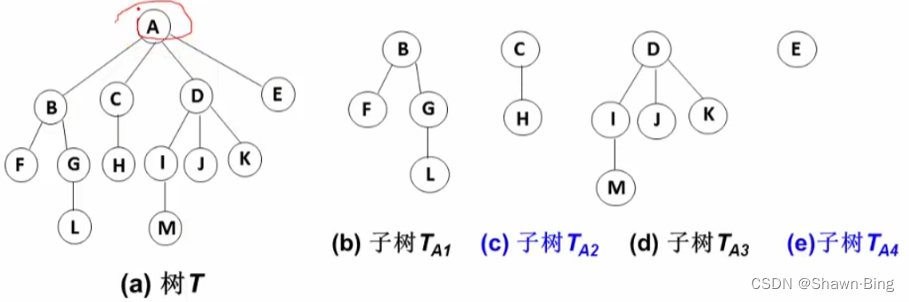
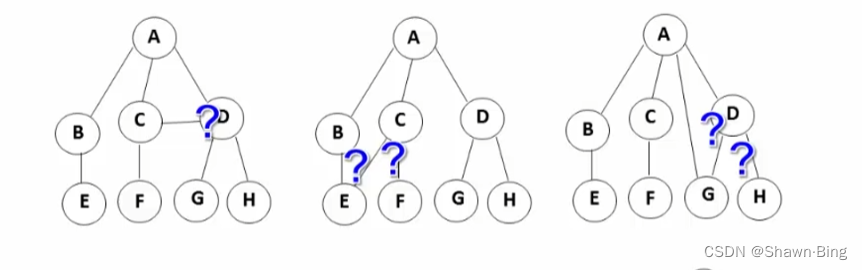
非树:
- 子树之间有相交
树:—— 一种保证结点联通方式最小的连接方式
- 子树之间不能相交
- 除根结点以外,每个结点有且仅有一个父结点
- 一颗N个结点的树有N-1条边
一些基本术语:
- 结点的度:结点子树个数(有几个直接相连的子结点)
- 树的度:树的所有结点中最大的度数(树所有结点里子树最多的那一项,子树的个数)
- 叶结点(Leaf):度为0的结点
- 父结点(Parent):有子树的结点是其子树的根节点的父结点
- 子结点(Child):也称孩子节点。若A结点是B结点的父结点,则称B结点是A结点的子结点。
- 兄弟结点(Sibiling):具有同一父结点的各结点彼此是兄弟结点
- 路径和路径长度:从结点n1到nk的路径为一个结点序列n1,n2,...,nk,ni是ni+1的父结点。路径所包含边的个数为路径的长度。
- 祖先结点(Ancestor):沿树根到某一结点路径上所有结点都是这个结点的祖先结点。(层数高的是层数低的祖先)
- 子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙
- 结点的层次(Level):规定根结点在一层,其它任一结点的层数是其父结点层数+1
- 树的深度(Depth):树中所有结点中的最大层次是这棵树的深度
3.1.5 树的表示
知道了树的抽象结构和基本概念,下面我们需要能在计算机中表示树这种结构。首先我们肯定是需要在已有的结构中选择一种。
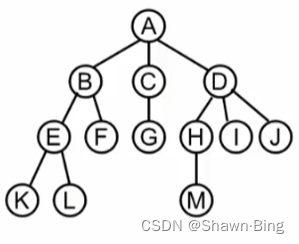
使用结构+链表
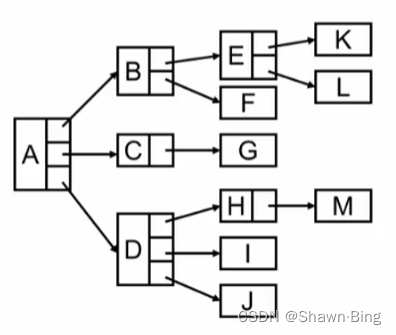
看似结构很像,实则在实现过程中,每个结点指向其他结点的个数并不相同,结构不一定能囊括所有情况。那如果将所有的结点都设计成一个形式,比如都留3个指针域,有的结点可能只用一个,但这样能保证结点结构统一,处理方便。但当树的体积非常庞大时候,这样的做法会造成巨大的浪费。
有一种较好的表示方法,同样是使用结构+链表的形式,所有结点结构相同。每个结点包含两个指针域,一个是FirstChild,指向这个结点的第一个孩子结点,另一个是NextSibiling,指向它的下一个兄弟结点。这种形式的树我们称为:二叉树(链表)
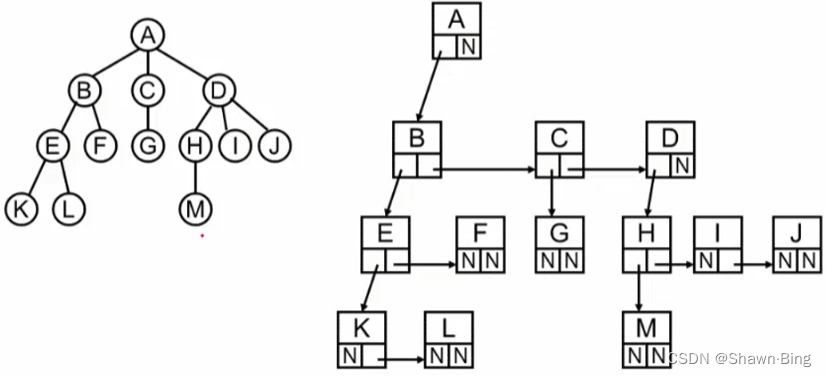
相关文章:

(浙大陈越版)数据结构 第三章 树(上) 3.1 树和树的表示
目录 3.1.1 引子(顺序查找) 什么是树 查找 3.1.2 引子 二分查找例子(BinarySearch) 二分查找 3.1.3 引子 二分查找实现 二分查找代码 二分查找的启示 3.1.4 树的定义 一些基本术语: 3.1.5 树的表示 3.1.1 引子(顺序查找…...

平抑风电波动的电-氢混合储能容量优化配置(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

#机器学习--重新看待线性回归
#机器学习--重新看待线性回归 引言普通视角的线性回归最大似然角度的线性回归总结 引言 本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简,适合二次学习的读者快速学习或查阅。 普通视角的线性回归 对于一组数据 { ( x 0 , y 0 ) , … ( x m…...

亚马逊,shopee,lazada卖家如何组建自己的测评团队
测评补单,这个话题在如今不管国内还是国外的电商行业已经是众所周知,它能够快速帮助自己的产品添加评论,获取排名,打造爆款,可以让用户更加真实、清晰、快捷的了解产品,以及产品的使用,快速上手…...

flink cdc 用mybatis-plus写到mysql5.6
背景 项目中需要做一个数据同步的功能, 在方案对比中,canal 与flink cdc 都有尝试。 起初在网上找的flink例子,要么只能支持mysql5.7以上版本,要么就是需要序列化各种bug,比如就不能直接使用 @Autowired xxxServer 来调用数据库层面的注入,getBaseMapper()为空 因为目…...
【C++】模板的一点简单介绍
模板 前言泛型编程函数模板概念格式函数模板的原理函数模板的实例化 类模板类模板的定义格式类模板的实例化 前言 这篇博客讲的是模板的一些基本知识,并没有那么深入,但是如果你是为了过期末考试而搜的这篇博客,我觉得下面讲的是够了的。 之…...
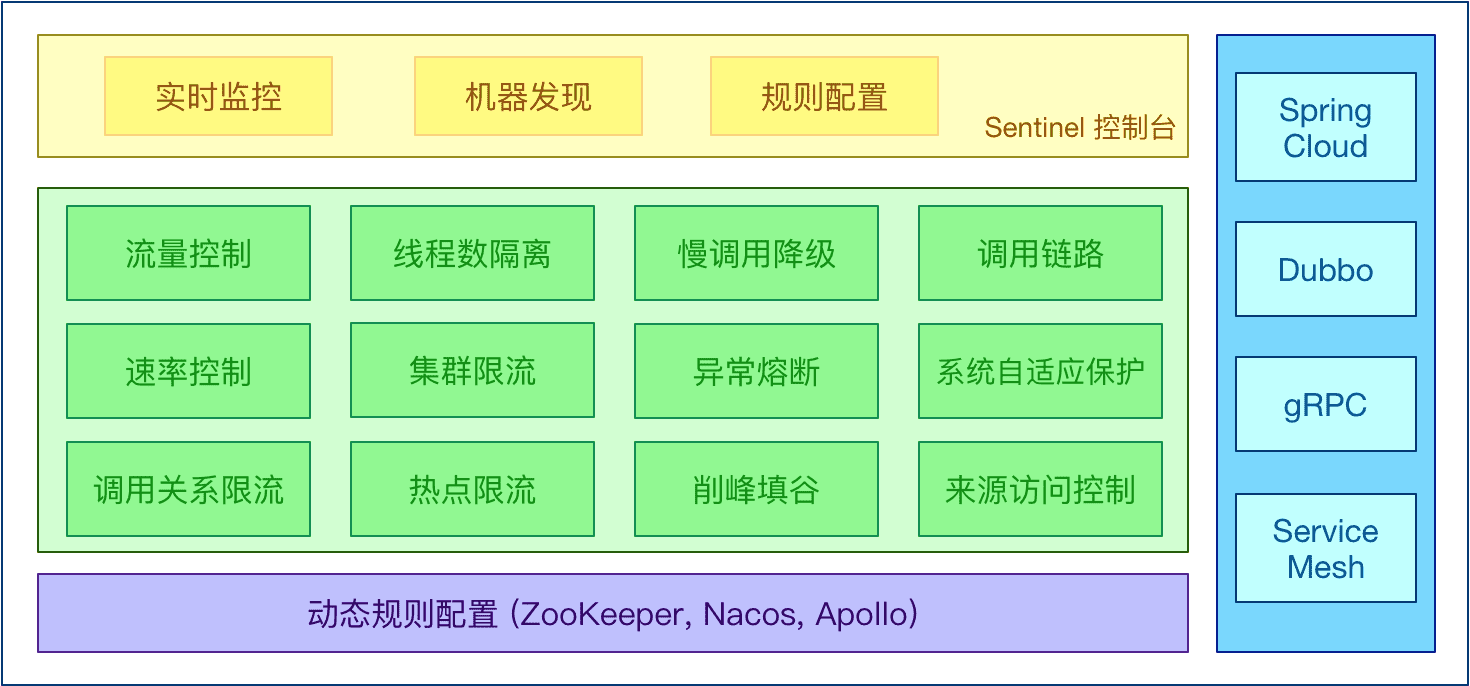
SpringCloud概述
前言 什么是微服务? 微服务是一种面向服务的架构(SOA)风格,其中,应用程序被构建为多个不同的小型服务的集合而不是单个应用程序。与单个程序不同的是,微服务让你可以同时运行多个独立的应用程序,而这些独立的应用…...

Metal入门学习:GPU并行计算大数组相加
一、编程指南PDF下载链接(中英文档) 1、Metal编程指南PDF链接 https://github.com/dennie-lee/ios_tech_record/raw/main/Metal学习PDF/Metal 编程指南.pdf 2、Metal着色语言(Metal Shader Language:简称MSL)编程指南PDF链接 https://github.com/dennie-lee/ios_te…...

关于在spyder,jupyter notebook下创建虚拟环境(pytorch,tensorflow)均有效
anaconda下载地址 https://www.anaconda.com/download/ 下载完成后打开anaconda目录下的 anaconda prompt 在命令行中输入下面的命令创建一个叫tf2.0的虚拟环境(“tf2.0”是建立的Conda虚拟环境的名字,可以自拟) conda create -n tf2.0 p…...

oracle 闪回恢复
oracle 闪回恢复 闪回恢复区主要通过3个初始化参数来设置和管理: db_recovery_file_dest:指定闪回恢复区的位置 db_recovery_file_dest_size:指定闪回恢复区的可用空间大小 db_flashback_retention_target:指定数据库可以回退的时…...

LeetCode 322 零钱兑换
题目: 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量…...

面试篇SpringMVC是什么以及工作原理
1,什么是SpringMVC呢? 它是Spring的一种设计模式,一款框架。 2,MVC分别代表什么? M代表模型即model的缩写,指业务逻辑层模型。V代表视图即View的缩写,指视图层。C则是controller的缩写ÿ…...

jQuery-层级选择器
<!DOCTYPE HTML> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"> <title>层级选择器</title> <style type"text/css"> …...

【Java数据结构】——第十节(下).选择排序与堆排序
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:Java初阶数据结构 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目…...
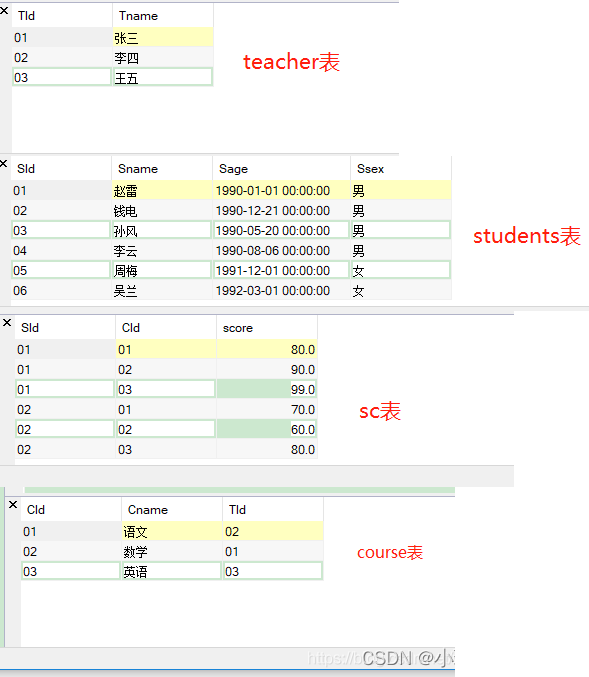
45道SQL题目陆续更新
文章目录 学习视频配置环境第一天内连接 外连接第二天第三天 学习视频 学习视频 配置环境 四张表 配置四张表的sql语句 #创建发据库 create database frogdata charsetutf8;use frogdata;# 学生表 Student create table Student( SId varchar(10), Sname var…...

在线PS软件有哪些不错的推荐
许多新的UI设计合作伙伴非常关心在线ps工具的选择。现在市场上有各种各样的ps网页替代工具,数量众多,令人眼花缭乱。本文简要介绍了10个在线PS工具,我相信一定有一个适合你! 1.即时设计 即时设计是一款在线 UI 设计工具…...
Java实现天气预报功能
如果要实现类似百度天气、手机App这样的天气预报功能该如何实现?首先想到的是百度... 背景: 最近公司做了一个项目,天气预报的功能也做上去了,不仅有实时天气、未来7天预报的功能、还有气象预警的功能。 天气包括基本天气、白天夜…...

python循环语句
while循环 Python中,while循环只要在条件(表达式)为真的情况下,就会一直重复执行相应的循环代码块。 while语句的语法格式如下: while 条件表达式:代码块while语句执行的具体流程为:首先判断…...
线程基础信息、synchronized 锁概念)
多线程基础(一)线程基础信息、synchronized 锁概念
1. 基本概念: 程序: 程序是一些保存在磁盘上的指令的有序集合,是静态的。程序包括:内存资源、IO资源、信号处理等。(如:XX.exe) 进程: 进程是程序执行的过程,包括了动态…...

JAVA期末考内容知识点的梳理
作者的话 前言:这些都是很基本的,还有很多没有写出来,重点在于考试复习,包括后四章的内容 前面内容请参考JAVA阶段考内容知识点的梳理 一、集合、流 课堂总结1集合 集合概念: 保存和盛装数据的容器,将许多…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
