#机器学习--重新看待线性回归
#机器学习--重新看待线性回归
- 引言
- 普通视角的线性回归
- 最大似然角度的线性回归
- 总结
引言
本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简,适合二次学习的读者快速学习或查阅。
普通视角的线性回归
对于一组数据 { ( x 0 , y 0 ) , … ( x m , y m ) } \{(x_{0},y_{0}),\dots(x_{m},y_{m})\} {(x0,y0),…(xm,ym)} 我们希望找到一个线性模型 y = w T x y=w^{T}x y=wTx 使得其在这组数据上拟合效果最好。既然要找最好,肯定就需要一个衡量指标。
最直观的理解就是,当所有点到直线的距离之和最小时,误差最小,拟合效果最好。即,使用 M S E t r a i n MSE_{train} MSEtrain 作为模型的衡量指标。此时我们得到优化目标: arg min w ∑ i m ( y i − w T x i ) 2 \argmin_{w}\sum_{i}^{m}(y_{i}-w^{T}x_{i})^{2} wargmini∑m(yi−wTxi)2
最大似然角度的线性回归
假设对于每个 y i y_{i} yi 都由正态分布 N ( w T x i , σ ) N(w^{T}x_{i},\sigma) N(wTxi,σ) 产生,其中 σ \sigma σ 是用户固定的某个常量。之所以这么假设,是因为如果要找到一个正态分布 N ( μ , σ ) N(\mu,\sigma) N(μ,σ) 能够使得点 ( x , y ) (x,y) (x,y) 被采样的概率最大,那么这个正态分布就是 N ( x , σ ) N(x,\sigma) N(x,σ) 。也就是说,对于每个样本都是由正态分布采样所得,根据最大似然的思想,令所有的 y i y_{i} yi 同时发生的可能性最大,即: arg max w ∑ i m l n [ 1 σ 2 π e − 1 2 ( y i − w T x i σ ) 2 ] \argmax_{w}\sum_{i}^{m}ln[\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{y_{i}-w^{T}x_{i}}{\sigma})^{2}}] wargmaxi∑mln[σ2π1e−21(σyi−wTxi)2] = > arg max w [ ∑ i m l n [ 1 σ 2 π ] − ∑ i m [ 1 2 σ 2 ( y i − w T x i ) 2 ] ] =>\argmax_{w}[\sum_{i}^{m}ln[\frac{1}{\sigma\sqrt{2\pi}}]-\sum_{i}^{m}[\frac{1}{2\sigma^{2}}(y_{i}-w^{T}x_{i})^{2}]] =>wargmax[i∑mln[σ2π1]−i∑m[2σ21(yi−wTxi)2]] = > arg min w ∑ i m ( y i − w T x i ) 2 =>\argmin_{w}\sum_{i}^{m}(y_{i}-w^{T}x_{i})^{2} =>wargmini∑m(yi−wTxi)2
总结
从最终结果来看,两者之间的优化目标是一样的,但从本质上来讲,最小二乘法只是最大似然在正态分布下的一种特殊情况。如果假设其它分布则会有不同的结果,如:
伯努利分布下,最大似然估计的结果就是逻辑回归。
多项式分布下,最大似然估计的结果就是softmax回归。
感兴趣的读者可以自行证明。
相关文章:

#机器学习--重新看待线性回归
#机器学习--重新看待线性回归 引言普通视角的线性回归最大似然角度的线性回归总结 引言 本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简,适合二次学习的读者快速学习或查阅。 普通视角的线性回归 对于一组数据 { ( x 0 , y 0 ) , … ( x m…...

亚马逊,shopee,lazada卖家如何组建自己的测评团队
测评补单,这个话题在如今不管国内还是国外的电商行业已经是众所周知,它能够快速帮助自己的产品添加评论,获取排名,打造爆款,可以让用户更加真实、清晰、快捷的了解产品,以及产品的使用,快速上手…...

flink cdc 用mybatis-plus写到mysql5.6
背景 项目中需要做一个数据同步的功能, 在方案对比中,canal 与flink cdc 都有尝试。 起初在网上找的flink例子,要么只能支持mysql5.7以上版本,要么就是需要序列化各种bug,比如就不能直接使用 @Autowired xxxServer 来调用数据库层面的注入,getBaseMapper()为空 因为目…...
【C++】模板的一点简单介绍
模板 前言泛型编程函数模板概念格式函数模板的原理函数模板的实例化 类模板类模板的定义格式类模板的实例化 前言 这篇博客讲的是模板的一些基本知识,并没有那么深入,但是如果你是为了过期末考试而搜的这篇博客,我觉得下面讲的是够了的。 之…...
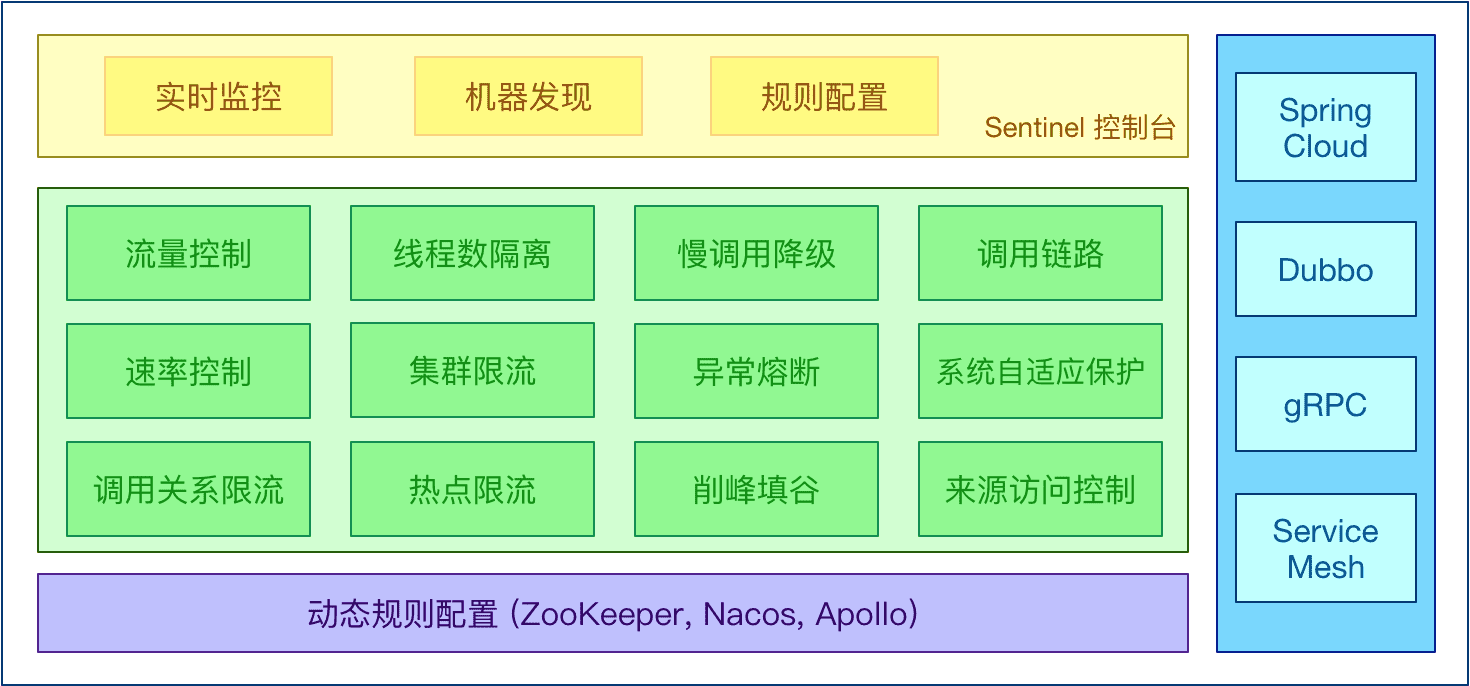
SpringCloud概述
前言 什么是微服务? 微服务是一种面向服务的架构(SOA)风格,其中,应用程序被构建为多个不同的小型服务的集合而不是单个应用程序。与单个程序不同的是,微服务让你可以同时运行多个独立的应用程序,而这些独立的应用…...

Metal入门学习:GPU并行计算大数组相加
一、编程指南PDF下载链接(中英文档) 1、Metal编程指南PDF链接 https://github.com/dennie-lee/ios_tech_record/raw/main/Metal学习PDF/Metal 编程指南.pdf 2、Metal着色语言(Metal Shader Language:简称MSL)编程指南PDF链接 https://github.com/dennie-lee/ios_te…...

关于在spyder,jupyter notebook下创建虚拟环境(pytorch,tensorflow)均有效
anaconda下载地址 https://www.anaconda.com/download/ 下载完成后打开anaconda目录下的 anaconda prompt 在命令行中输入下面的命令创建一个叫tf2.0的虚拟环境(“tf2.0”是建立的Conda虚拟环境的名字,可以自拟) conda create -n tf2.0 p…...

oracle 闪回恢复
oracle 闪回恢复 闪回恢复区主要通过3个初始化参数来设置和管理: db_recovery_file_dest:指定闪回恢复区的位置 db_recovery_file_dest_size:指定闪回恢复区的可用空间大小 db_flashback_retention_target:指定数据库可以回退的时…...

LeetCode 322 零钱兑换
题目: 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量…...

面试篇SpringMVC是什么以及工作原理
1,什么是SpringMVC呢? 它是Spring的一种设计模式,一款框架。 2,MVC分别代表什么? M代表模型即model的缩写,指业务逻辑层模型。V代表视图即View的缩写,指视图层。C则是controller的缩写ÿ…...

jQuery-层级选择器
<!DOCTYPE HTML> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"> <title>层级选择器</title> <style type"text/css"> …...

【Java数据结构】——第十节(下).选择排序与堆排序
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:Java初阶数据结构 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!! 文章目…...
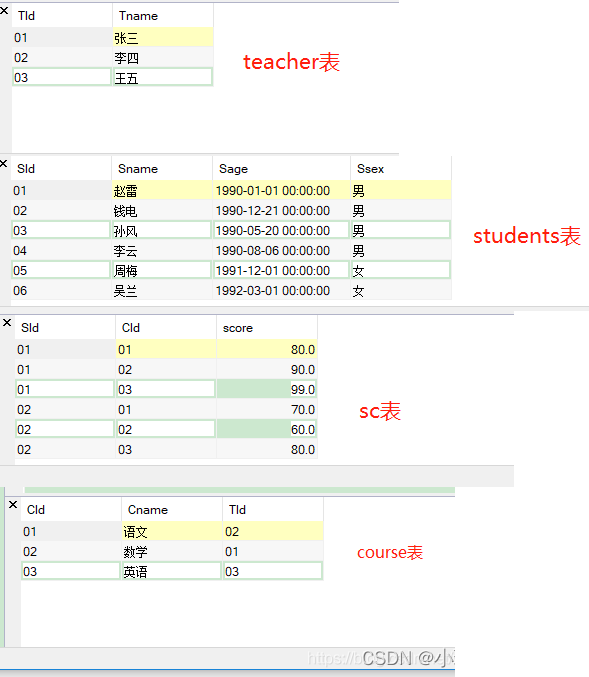
45道SQL题目陆续更新
文章目录 学习视频配置环境第一天内连接 外连接第二天第三天 学习视频 学习视频 配置环境 四张表 配置四张表的sql语句 #创建发据库 create database frogdata charsetutf8;use frogdata;# 学生表 Student create table Student( SId varchar(10), Sname var…...

在线PS软件有哪些不错的推荐
许多新的UI设计合作伙伴非常关心在线ps工具的选择。现在市场上有各种各样的ps网页替代工具,数量众多,令人眼花缭乱。本文简要介绍了10个在线PS工具,我相信一定有一个适合你! 1.即时设计 即时设计是一款在线 UI 设计工具…...
Java实现天气预报功能
如果要实现类似百度天气、手机App这样的天气预报功能该如何实现?首先想到的是百度... 背景: 最近公司做了一个项目,天气预报的功能也做上去了,不仅有实时天气、未来7天预报的功能、还有气象预警的功能。 天气包括基本天气、白天夜…...

python循环语句
while循环 Python中,while循环只要在条件(表达式)为真的情况下,就会一直重复执行相应的循环代码块。 while语句的语法格式如下: while 条件表达式:代码块while语句执行的具体流程为:首先判断…...
线程基础信息、synchronized 锁概念)
多线程基础(一)线程基础信息、synchronized 锁概念
1. 基本概念: 程序: 程序是一些保存在磁盘上的指令的有序集合,是静态的。程序包括:内存资源、IO资源、信号处理等。(如:XX.exe) 进程: 进程是程序执行的过程,包括了动态…...

JAVA期末考内容知识点的梳理
作者的话 前言:这些都是很基本的,还有很多没有写出来,重点在于考试复习,包括后四章的内容 前面内容请参考JAVA阶段考内容知识点的梳理 一、集合、流 课堂总结1集合 集合概念: 保存和盛装数据的容器,将许多…...
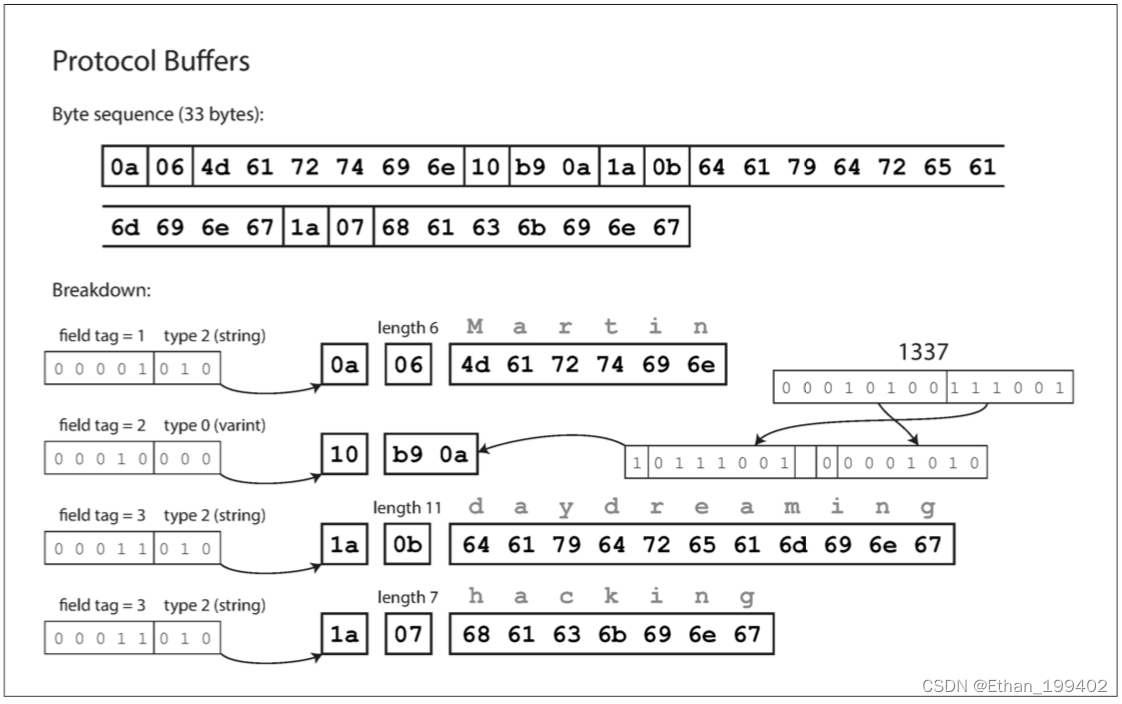
为什么要使用Thrift与Protocol Buffers?
编码数据的格式 程序通常(至少)使用两种形式的数据: 在内存中,数据保存在对象、结构体、列表、数组、散列表、树等中。 这些数据结构针对 CPU 的高效访问和操作进行了优化(通常使用指针)。如果要将数据写…...

oa是什么意思?oa系统哪个好用?
一、oa是什么意思 oa(Office Automation办公自动化)是一种将智能化科技应用于企业管理中的应用系统。它可以通过电脑网络、互联网等技术手段,将企业的各种业务流程、各种业务数据进行集成和处理,将各种业务流程和各种业务数据统一…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
