【数据结构】优先级队列----堆
优先级队列----堆
- 优先级队列
- 堆
- 堆的创建
- 堆的插入:
- 堆的删除:
- PriorityQueue的特性
- PriorityQueue的构造与方法
优先级队列
优先级队列: 不同于先进先出的普通队列,在一些情况下,优先级高的元素要先出队列。而这种队列需要提供两个基本的操作:返回最高优先级对象 和 添加新的对象。
(JDK1.8中,优先级队列底层使用的是 堆 数据结构,而堆则是在完全二叉树的基础上进行了调整)
堆
堆: 将一组集合的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 为 小堆,Ki >= K2i+1 且 Ki >= K2i+2 为 大堆。i = 0,1,2…,将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。例如:
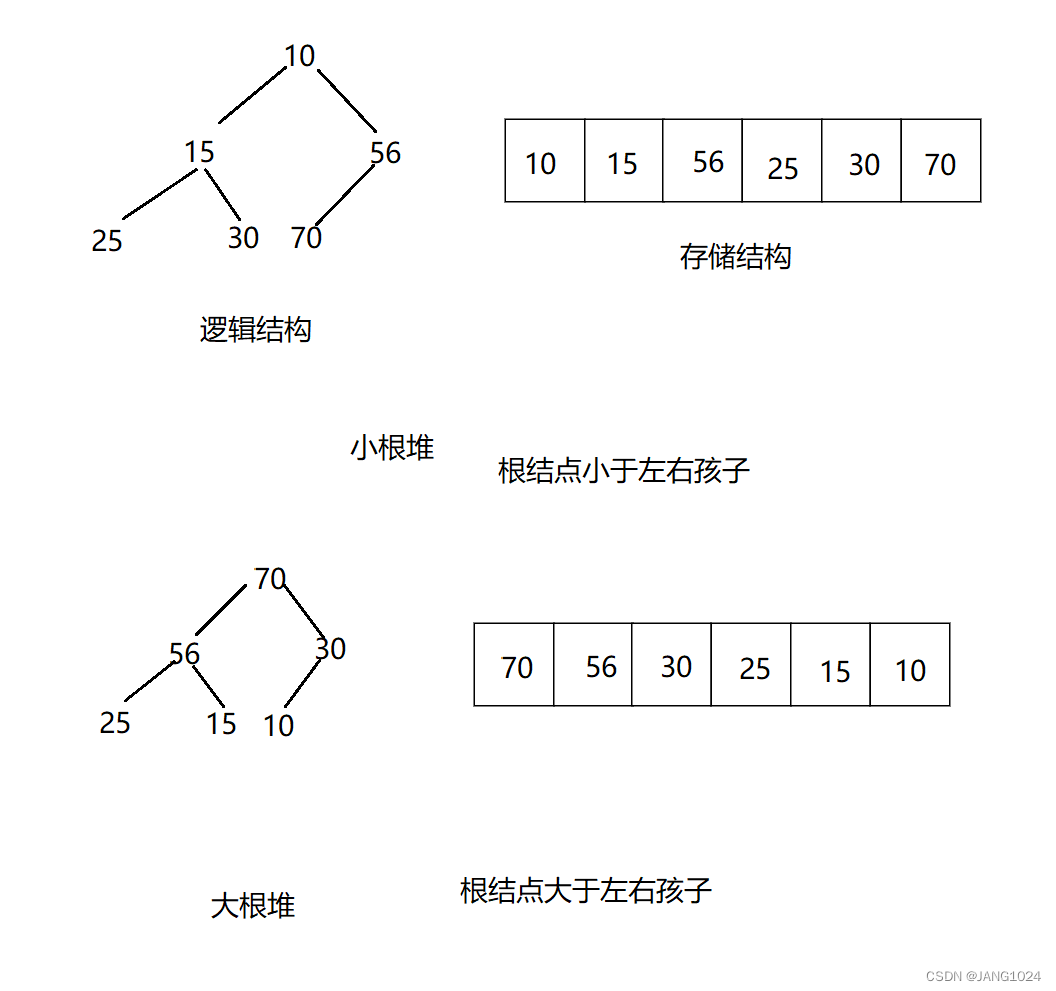
堆的两个性质:
堆中某个结点的值总是不大于或不小于其父节点的值。
堆总是一棵完全二叉树。
堆的存储方式:
堆是一棵完全二叉树,因此可以用层序的规则采用顺序的方式来高效存储,但对于非完全二叉树,就不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节
点,就会导致空间利用率比较低。
如果 i 表示孩子结点,则父节点为 (i - 1)/2。
如果 i 表示根结点,左孩子则为 2i + 1,右孩子为 2i + 2。
堆的创建
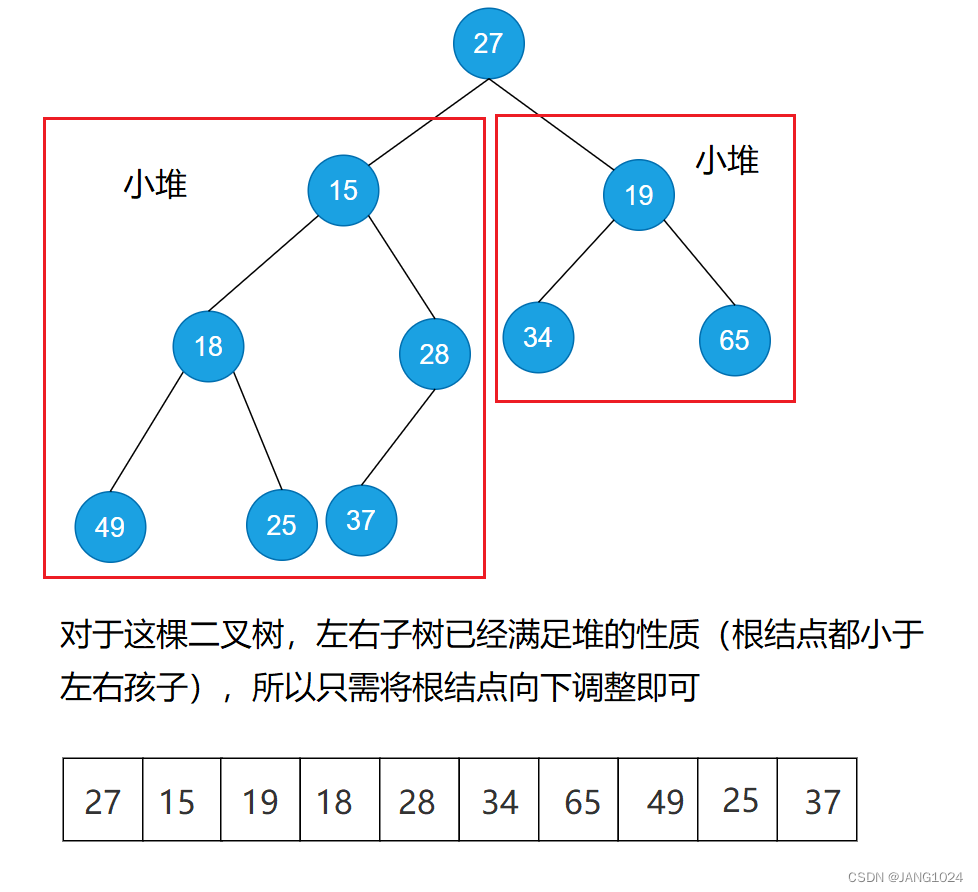
向下调整过程(以小根堆为例):
- 让 parent 标记需要调整的节点,child 标记 parent 的左孩子(完全二叉树中,一定先有左孩子)
- 如果 parent 的左孩子存在(child < size),进行以下操作,直到 parent 的左孩子不存在:
找到左右孩子中较小的结点,和 parent 进行比较,若 parent 小,则调整结束。若 parent 大,则进行交换。交换后,可能会使原来满足堆的子树发生改变,所以需要继续向下调整。
例如:
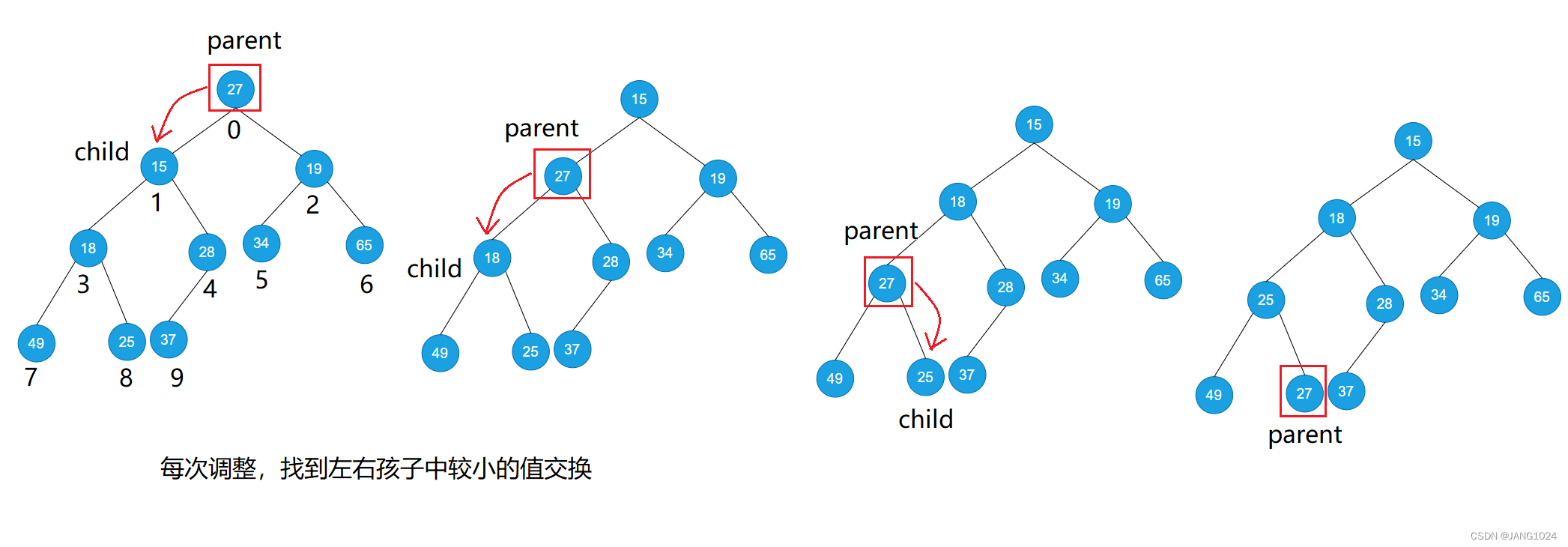
代码:
public class TestHeap {public int[] elem;public int usedSize;public TestHeap() {this.elem = new int[10];}//初始化public void initElem(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}public void createHeap() {//循环调用for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(parent, usedSize);}}//向下调整 len为当前有效数据个数private void shiftDown(int parent, int len) {int child = 2 * parent + 1;//最起码 要有左孩子while (child < len) {//一定是有右孩子的情况下if (child + 1 < len && elem[child] > elem[child + 1]) {//保证 child指向较小值child++;}if (elem[child] < elem[parent]) {//孩子结点小于父节点 交换int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//继续调整下面子树parent = child;child = 2 * parent + 1;} else {break;}}}
}
建堆的时间复杂度:

堆的插入:
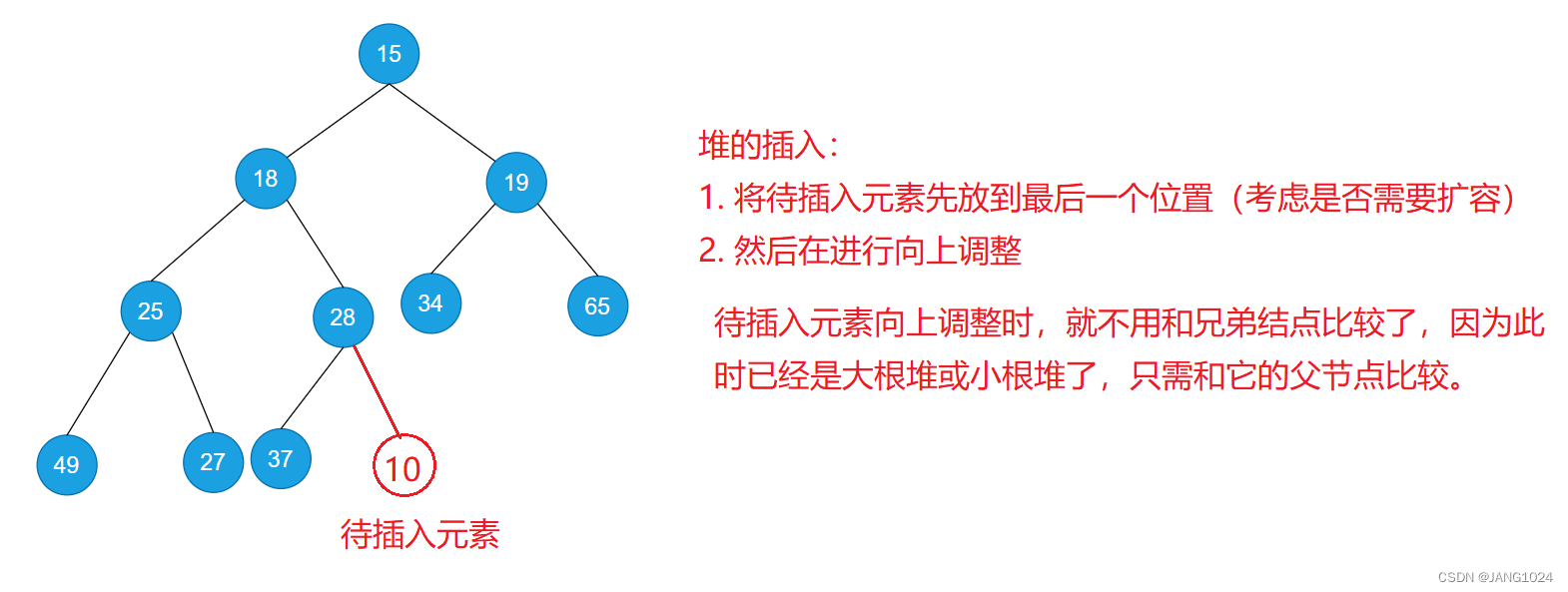
代码:
public void offer(int val) {if (isFull()) {//满了扩容elem = Arrays.copyOf(elem, 2 * elem.length);}//放到最后一个位置,长度加一elem[usedSize++] = val;//向上调整shiftUp(usedSize-1);}public boolean isFull() {return usedSize == elem.length;}private void shiftUp(int child) {int parent = (child - 1) / 2;while (child > 0) {if (elem[child] < elem[parent]) {int tmp = elem[child];elem[child] = elem[parent];elem[parent] = tmp;//继续往上走child = parent;parent = (child - 1) / 2;}else {break;}}}
堆的删除:
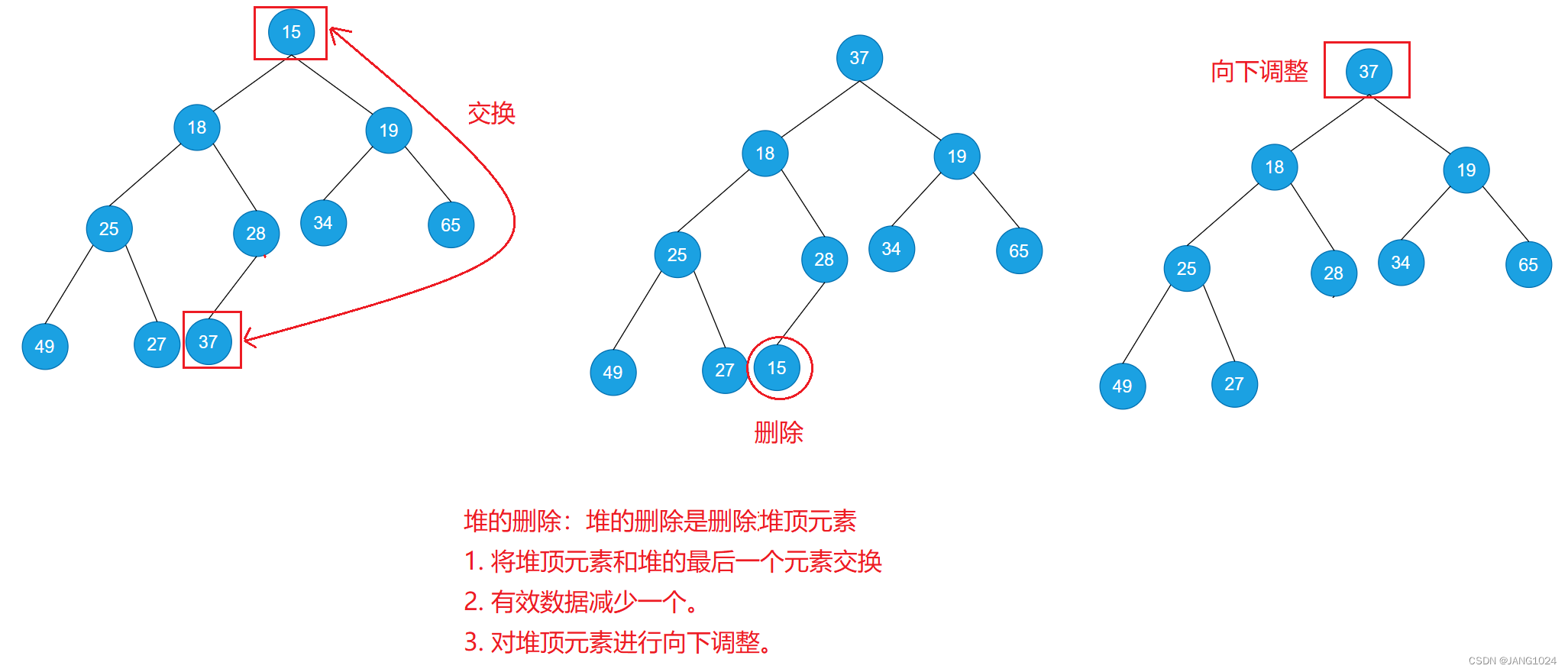
代码:
public void pop() {if (isEmpty()) {return;}//交换int tmp = elem[0];elem[0] = elem[usedSize - 1];elem[usedSize - 1] = tmp;//有效数据个数减一usedSize--;//向下调整shiftDown(0, usedSize);}public boolean isEmpty() {return usedSize == 0;}
PriorityQueue的特性
Java 集合框架中提供了 PriorityQueue 和 PriorityBlockingQueue 两种类型的优先级队列,PriorityQueue 是线程不安全的,PriorityBlockingQueue 是线程安全的,这里主要介绍PriorityQueue。
使用 PriorityQueue 需要注意:
-
使用时必须导入 PriorityQueue 所在的包(import java.util.PriorityQueue;)。
-
PriorityQueue 中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException 异常。
只插入一个元素时,并不会报错:
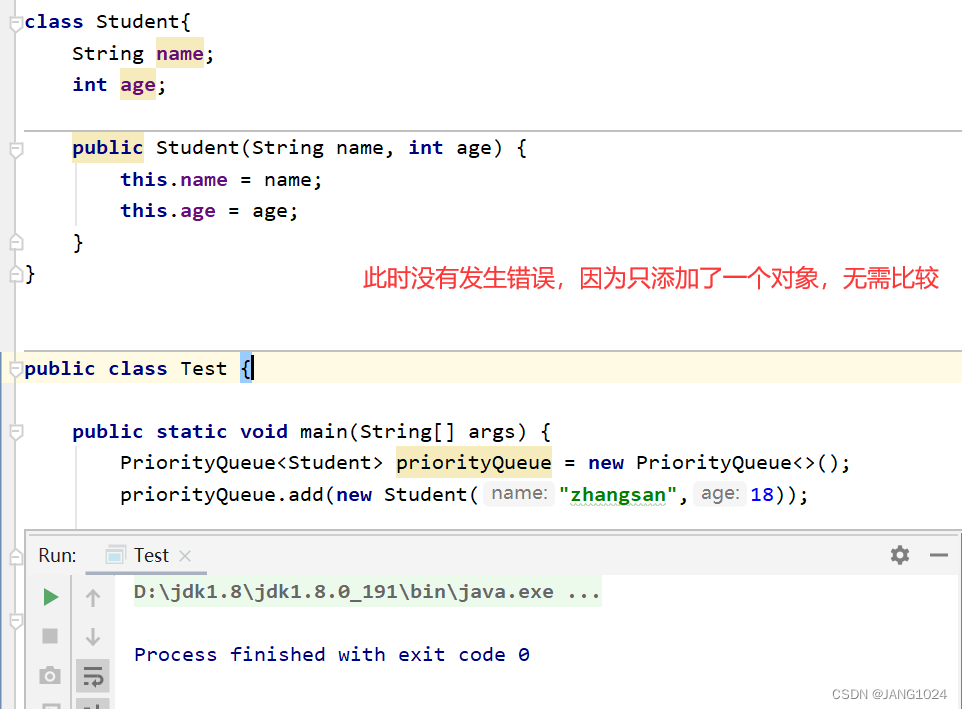
插入多个元素就会报错:
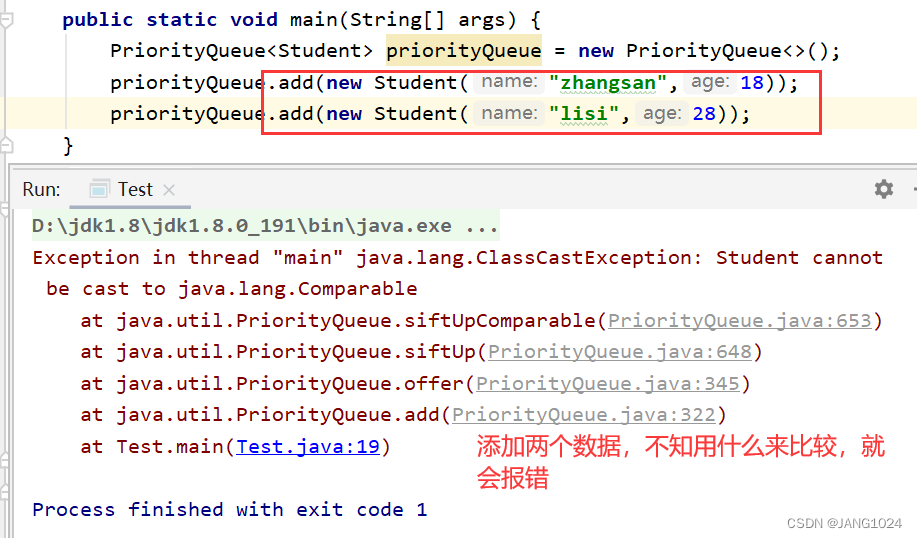
-
不能插入 null 对象,否则会抛出 NullPointerException。
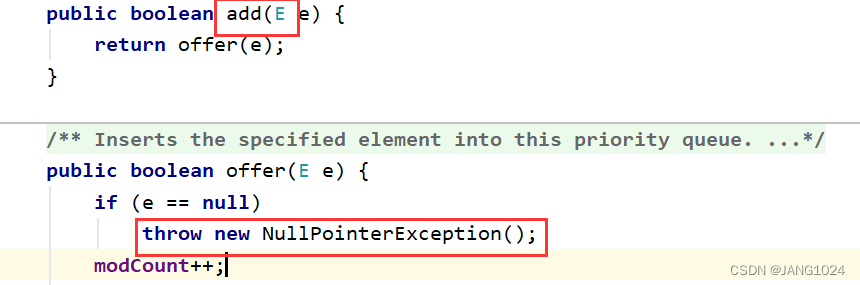
-
内部可以自动扩容。

-
插入和删除元素的时间复杂度为 O(log₂N)。
-
PriorityQueue 底层使用的是堆数据结构。
-
PriorityQueue 默认情况下是小堆。
PriorityQueue的构造与方法
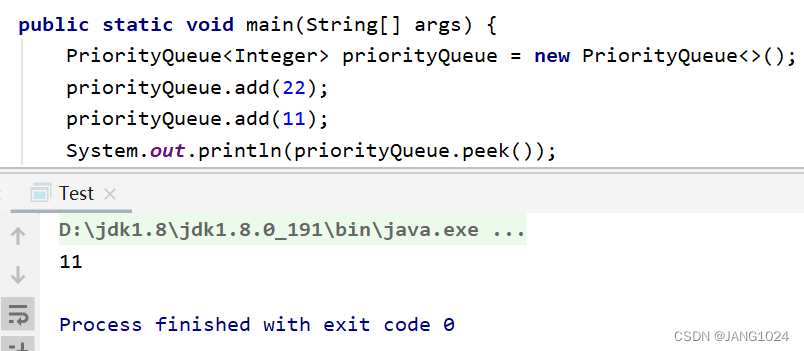
PriorityQueue 的几种构造方法:
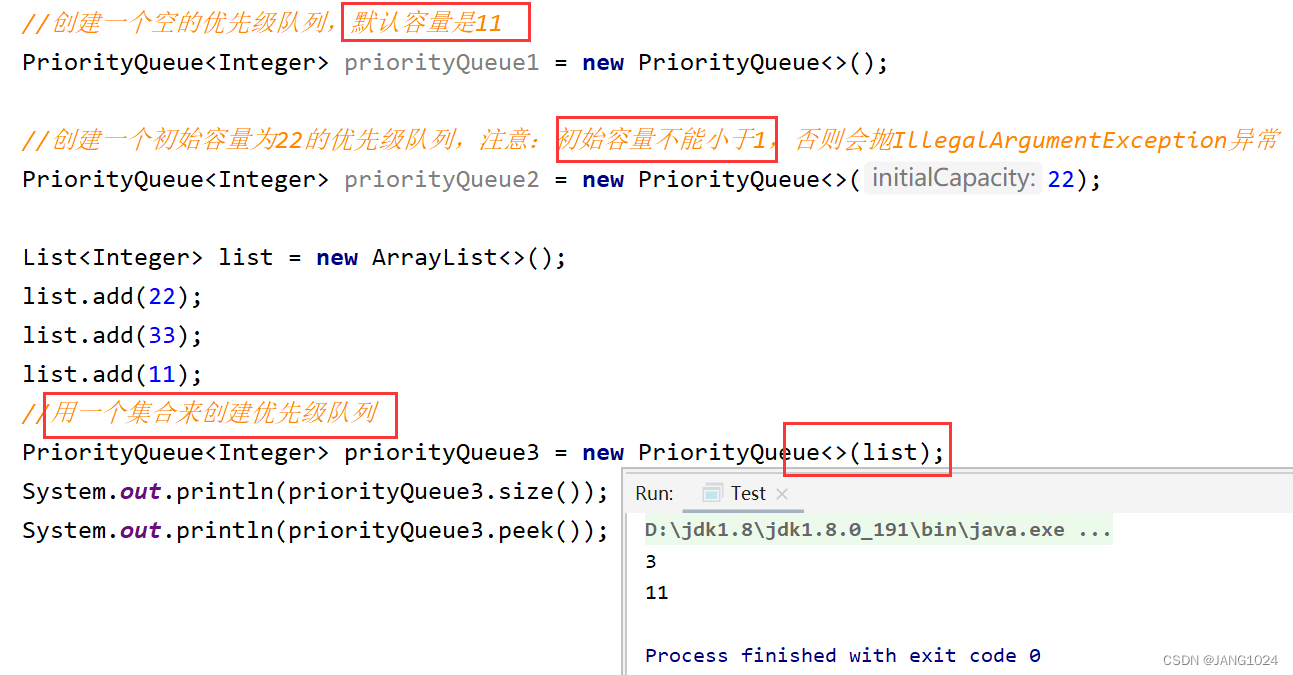
PriorityQueue 的方法:
PriorityQueue 的方法和其它数据结构类似:
Top-k 问题: 最大或者最小的前k个数据。例如求一组数据中前 k 个最小的数据。
题目链接:leetcode----面试题 17.14. 最小K个数
题目描述:
思路一:我们可以初始化一个数组大小的堆,然后遍历数组的同时将元素放进堆中,默认是小根堆,所以取 k 次堆顶元素即可(删除堆顶元素后,会调整堆中的数据)。
代码:
public int[] smallestK(int[] arr, int k) {//存储最小K个数的数组int[] ret = new int[k];if (arr == null || k == 0) {return ret;}// 以数组长度初始化一个小根堆Queue<Integer> minHeap = new PriorityQueue<>(arr.length);//遍历数组 放进小根堆for (int value : arr) {minHeap.offer(value);}//取 k个堆顶元素for (int i = 0; i < k; i++) {ret[i] = minHeap.poll();}return ret;
}
上面这段代码会使时间复杂度升高,每添加或删除一个元素,就会调整一个接近数组长度的堆。
思路二:要求最小 k 个数,我们将数组里的前 k 个元素添加到一个大小为 k 的大根堆,因为是大根堆,所以堆顶元素是堆中最大的元素,然后遍历数组剩下的元素,如果数组剩下的元素比堆顶元素小,我们就删除堆顶元素,并添加数组的元素,如果数组剩下的元素比堆顶元素大,它就不会是前 k 个最小数。
代码:
public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];if (arr == null || k == 0) {return ret;}//提供比较器,重写compare方法,此时建立的就是大根堆Queue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});//将数组前k个元素添加到大根堆中for (int i = 0; i < k; i++) {maxHeap.offer(arr[i]);}//遍历数组未添加到堆中的元素for (int i = k; i < arr.length; i++) {//因为是求最小值,所以如果比大根堆的堆顶元素小,就删除堆顶元素,并添加这个元素到堆中if (arr[i] < maxHeap.peek()) {maxHeap.poll();maxHeap.offer(arr[i]);}}//将堆中的k个元素添加中数组中for (int i = 0; i < k; i++) {ret[i] = maxHeap.poll();}return ret;
}
这段代码中,只建立了 k 个容量大小的堆,调整的个数就比第一段代码少。
对于求一组数据中前 k 个最大或最小的元素时,数据少时我们可以排序,但对于数据特别多时,还是采用堆的方式比较合适。步骤如下:
- 用数据集合中前K个元素来建堆。
求前 k 个最大的元素,则建小堆
求前 k 个最小的元素,则建大堆 - 用剩余的 N-K 个元素依次与堆顶元素来比较,不满足则替换堆顶元素,堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。
相关文章:

【数据结构】优先级队列----堆
优先级队列----堆优先级队列堆堆的创建堆的插入:堆的删除:PriorityQueue的特性PriorityQueue的构造与方法优先级队列 优先级队列: 不同于先进先出的普通队列,在一些情况下,优先级高的元素要先出队列。而这种队列需要提…...
Python深度学习实战PyQt5信号与槽的连接
本文讲解信号与槽的连接机制,详细示范各种类型的信号/槽连接的实现方法,这是图形用户界面的核心内容。还将介绍面向对象的程序设计,这是图形用户界面的基本思想目录1. 信号与槽(Signals and slots)信号与槽机制是 PyQt…...
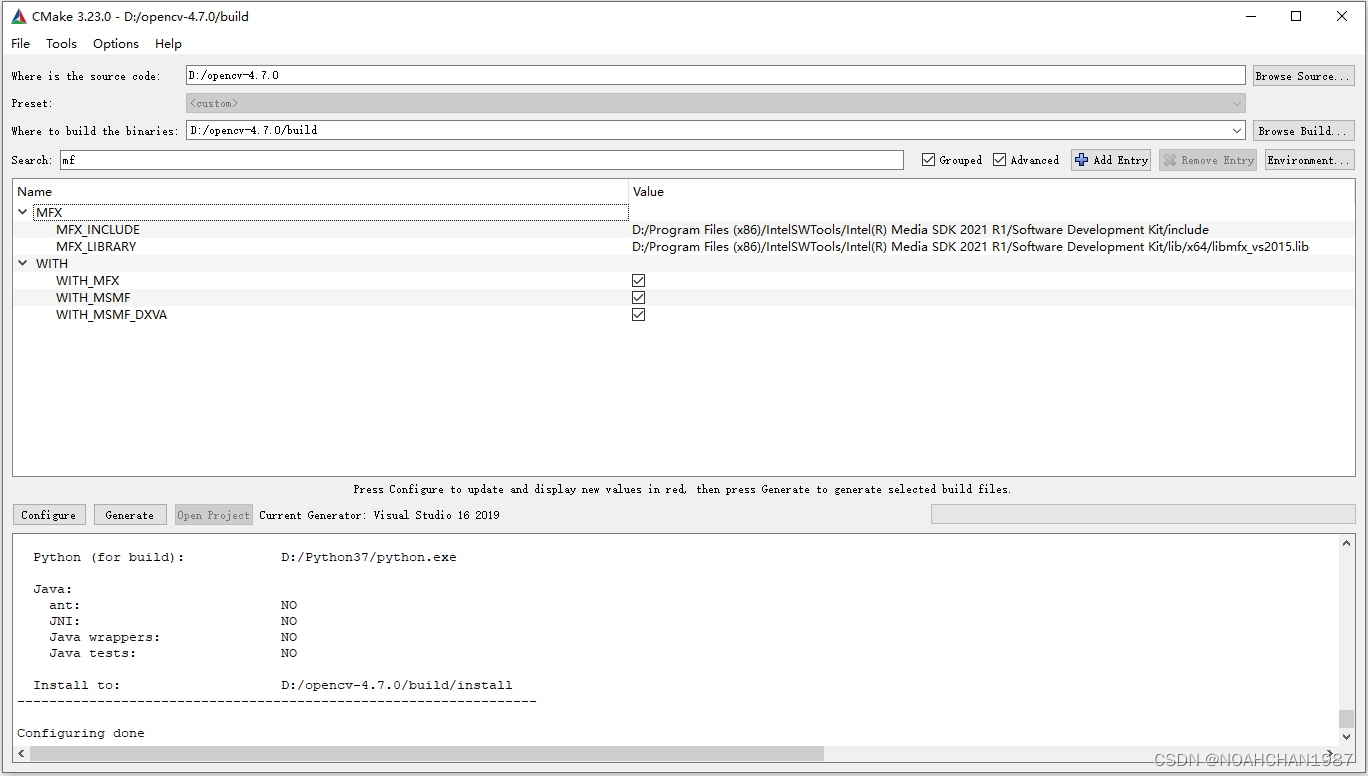
Window 10 OpenCV 打开罗技(Logitech)摄像头速度慢问题解决
采用最新版OpenCV 4.7.0 摄像头对罗技摄像头进行视频图像抓取时,发现存在打开摄像头慢的问题。 测试环境如下: 系统Windows 10 专业版CPUIntel i7-7700K 4.20GHz 摄像头型号罗技Logitech C930c 网络摄像头OpenCV版本4.7.0语言C 测试结果表明ÿ…...
基于yolo的小球位置实时检测
基于yolo的小球位置实时检测 Yolo安装 操作系统:ubuntu 安装cuda和opencv git clone https://github.com/pjreddie/darknet.git cd darknet 修改Makefile文件,使GPU1,OPENCV1 make 2. 数据集处理 2.1 制作数据集 将小球放在摄像头前…...
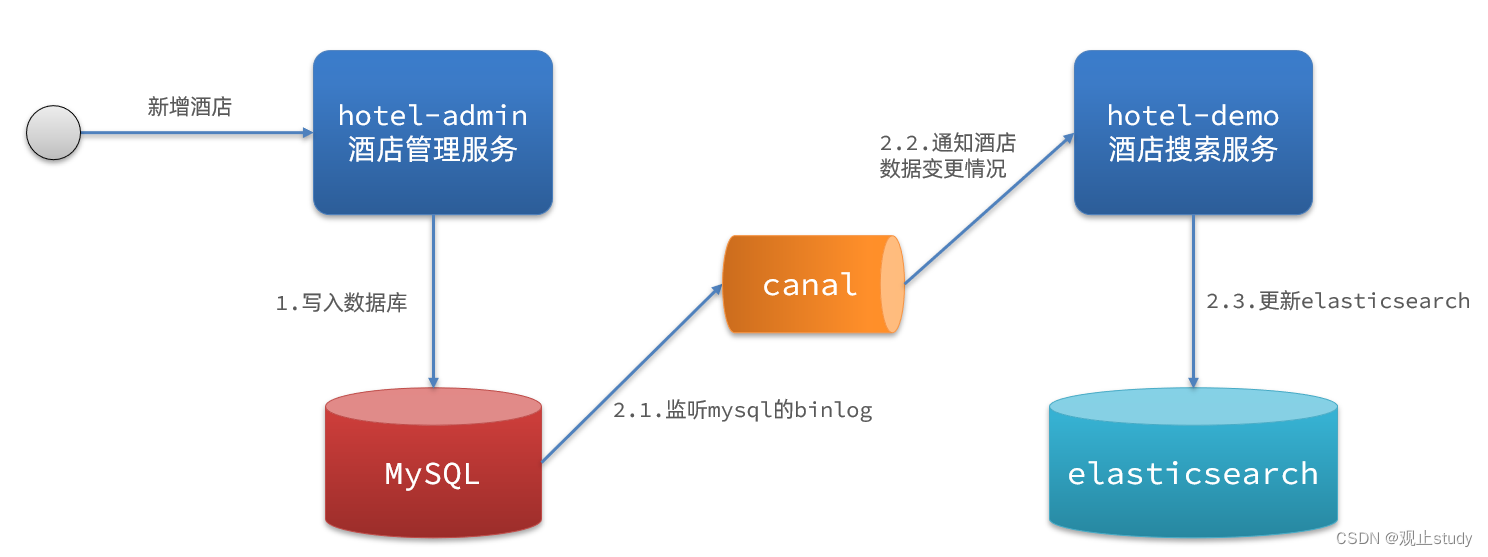
【微服务】Elasticsearch数据聚合自动补全数据同步(四)
🚗Es学习第四站~ 🚩Es学习起始站:【微服务】Elasticsearch概述&环境搭建(一) 🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 在第二站的学习中,我们已经导入了大量数据到es中&…...
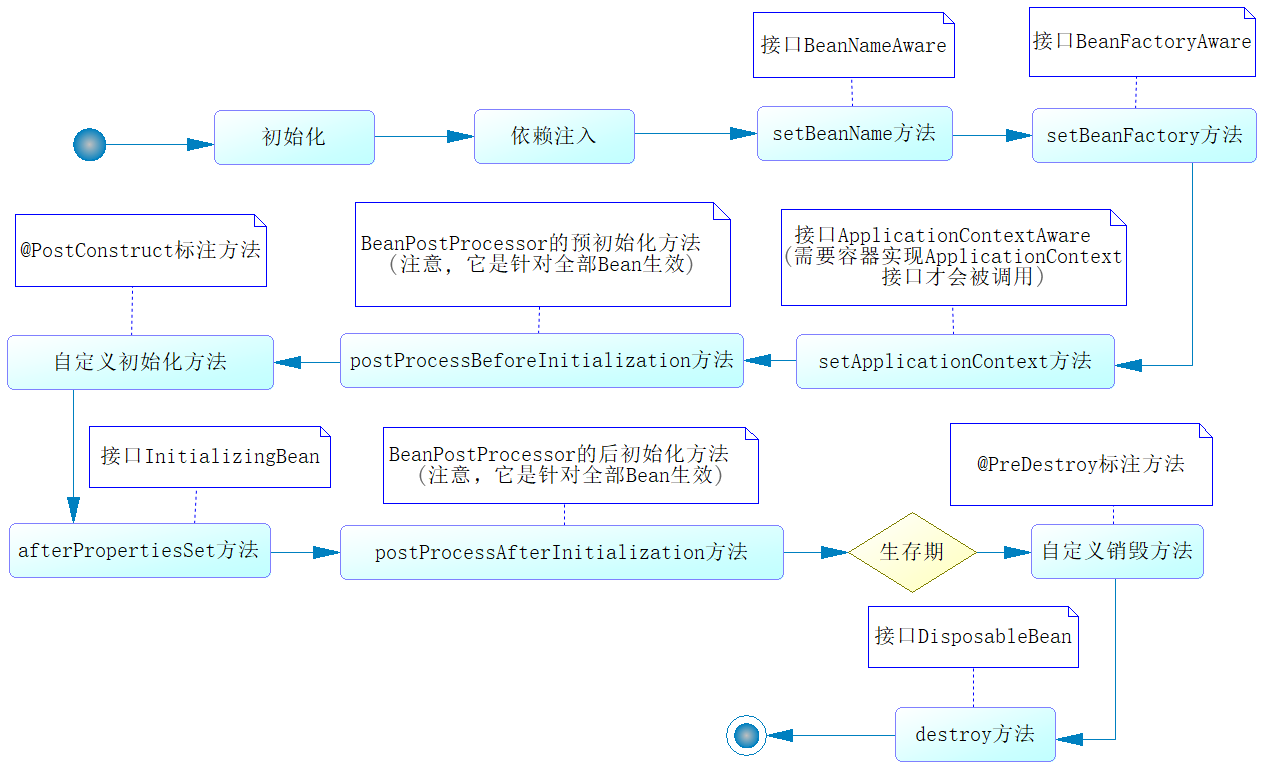
java面试题(十七)spring
2.1 请你说说Spring的核心是什么 参考答案 Spring框架包含众多模块,如Core、Testing、Data Access、Web Servlet等,其中Core是整个Spring框架的核心模块。Core模块提供了IoC容器、AOP功能、数据绑定、类型转换等一系列的基础功能,而这些功能…...

你知道 BI 是什么吗?关于 BI 系统的概述
BI 作为信息化建设中的关键一环,在企业中通常起到承上启下的作用,下能连接打通企业业务系统数据库,将各部门数据分类分级统一储存到数据仓库,简化存储取数流程,减少人力、时间成本;上能提供数据可视化报表…...
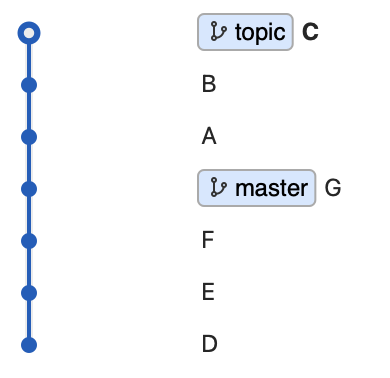
git:详解git rebase命令
背景 今天无意中打开 git 官网,发现 git 命令还是很多的,然而我们常用的就那几个,今天来学习一个也不怎么常用的命令 rebase 官网链接 都说学一个东西最好的方式就是读他的 官方文档,这里我读了一遍,把一些核心的地…...

第四章——随机变量的数字特征
文章目录1、数字特征的定义2、数学期望(均值)2.1、数学期望的定义及性质2.1.1、定义2.1.2、性质2.2、数学期望相关例题2.3、Yg(X)的数学期望2.4、Zg(X,Y)的数学期望2.5、随机变量函数的数学期望例题3、方差3.1、方差的定义与性质3.2、相关例题3.3、切比雪…...

vue2源码阅读理解-响应式数据原理
首先明确,vue2是如何实现响应式的? 通过object.defineProperty观察者模式实现,在创建vue实例的过程中,也就是介于beforecomputed~computed的过程中,会执行如下函数initState export function initState (vm: Componen…...
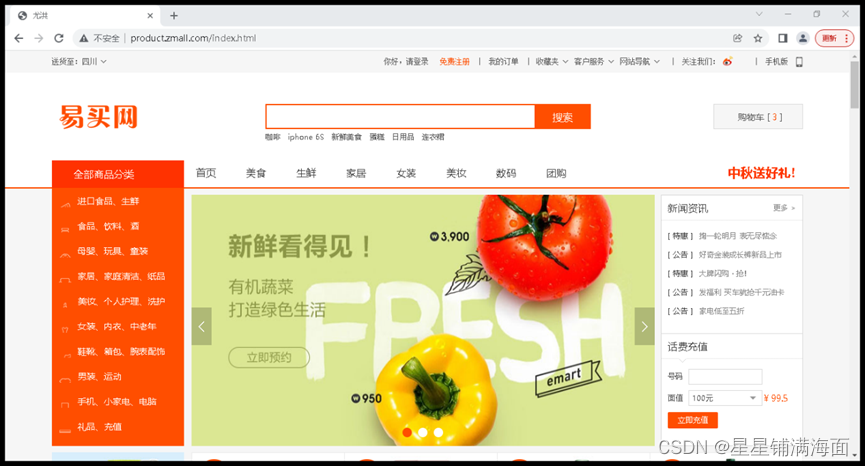
服务调用分布式session
目录一、nginx动静分离二、服务调用1、创建配置zmall-cart购物车模块2、创建配置zmall-order订单模块3、服务调用三、spring session实战1、什么是Spring Session2、为什么要使用Spring Session3、错误案例展示4、配置spring-session四、二级域名问题五、用户登录一、nginx动静…...

Maven知识点-插件-maven-surefire-plugin简介
Maven本身并不是一个单元测试框架,Java 世界中主流的单元测试框架为JUnit 和TestNG。 Maven 所做的只是在构建执行到特定生命周期阶段的时候,通过插件来执行JUnit或者TestNG的测试用例。 这一插件就是maven-surefire-plugin,可以称之为测试…...

如何借力Alluxio推动大数据产品性能提升与成本优化?
内容简介 随着数字化不断发展,各行各业数据呈现海量增长的趋势。存算分离将存储系统和计算框架拆分为独立的模块,Alluxio作为如今主流云数据编排软件之一,为计算型应用(如 Apache Spark、Presto)和存储系统࿰…...
(脚本包含,父子脚本))
linux shell脚本被包含是什么意思?.命令和source命令(在脚本中运行脚本,脚本中调用脚本)(脚本包含,父子脚本)
在 shell 编程中,当一个 shell 脚本被另一个 shell 脚本包含,即用 . 或 source 命令包含,则被包含的脚本在当前 shell 进程内执行,并且可以访问当前 shell 进程的环境变量和函数。 此时,$0 代表的是主脚本的名称&#…...

MySQL进阶篇之锁(lock)
05、锁 5.1、概述 1、介绍 锁是计算机协调多个进程或线程并发访问某一资源的机制。在数据库中,除传统的计算资源(CPU、RAM、I/O)的争用以外,数据也是一种供许多用户共享的资源。如何保证数据并发访问的一致性、有效性是所有数据…...

TMDSEVM6657LS评估板恢复出厂默认状态
TMDSEVM6657LS评估板恢复出厂默认状态 前言 TMDSEVM6657LS评估板特别适用于DSP开发的初学者,但有时候拿到手的开发板几经流转,被别人修改过,也可能自己烧录过程出错,导致开发板的状态未知等原因,需要恢复到出厂默认状…...

聊一聊,我对DDD的关键理解
作者:闵大为 阿里业务平台解决方案团队 当我们在学习DDD的过程中,感觉学而不得的时候,可能会问:我们还要学么?这的确引人深思。本文基于工作经验,尝试谈谈对DDD的一些理解。 一、序 《阿甘正传》中…...
—— 认识复杂度和简单排序算法)
算法笔记(一)—— 认识复杂度和简单排序算法
时间复杂度是在一个算法流程中,常数操作的数量级指标。(最差情况下的算法表现) 比较两个算法的优劣,在足够的空间下,看时间复杂度指标,若相同,需要在大数据运行下来判断两个算法的“常数项指标…...
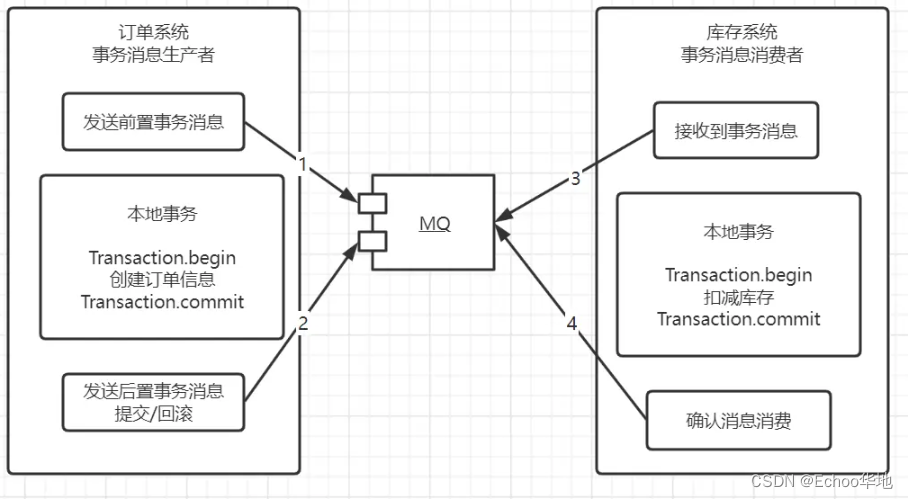
MQ消息中间件常见题及解决办法
目录儿常见MQRocketMQ2、RocketMQ测试可用MQ常见问题1、幂等性问题2、如何保证消息不丢失3、消息积压问题4、事务消息设计分析常见MQ RocketMQ RocketMQ又四部分组成 NameServer 同步Broker服务信息,给消费者和生产者提供可用Broker的服务信息。Broker 消息存储业…...
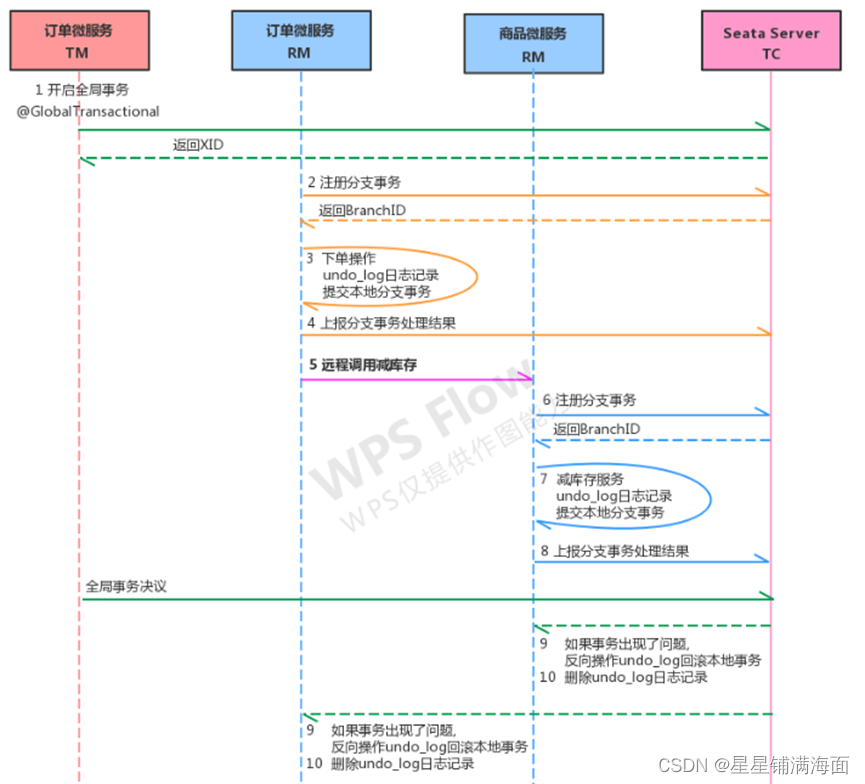
网关服务限流熔断降级分布式事务
目录一、网关服务限流熔断降级二、Seata--分布式事务1、分布式事务基础①事务②本地事物③分布式事务④分布式事务的场景2、分布式事务解决方案①全局事务②最大努力通知③TCC事务3、Seata介绍4、Seata实现分布式事务控制①案例基本代码(异常模拟)②启动…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
