【计算机网络期末复习】第六章 应用层
✍个人博客:https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📣专栏定位:为想复习学校计算机网络课程的同学提供重点大纲,帮助大家渡过期末考~
📚专栏地址:https://blog.csdn.net/Newin2020/article/details/129036672
❤️如果有收获的话,欢迎点赞👍收藏📁,您的支持就是我创作的最大动力💪
第六章 应用层
考点
- DNS解析,背后的运行机制需要清楚,可能是大题也可能是小题
- 电子邮件会考,考得比较基础,知道基础的即可
- 文件传输协议,可能会有小题像选择判断
- 万维网考得很少,很简单,稍微了解即可
- 协议传输的时间计算考试考得很少,考研考得多
- HTTP考得也少
- HTML不会考

1. 应用层概述
应用层对应用程序的通信提供服务。
应用层的功能:
- 文件传输、访问和管理
- 电子邮件
- 虚拟终端
- 查询服务和远程作业登录
应用层的重要协议:
- FTP
- SMTP、POP3
- HTTP
- DNS

2. 域名解析系统DNS
域名解析: 根据域名找IP地址
域名结构:
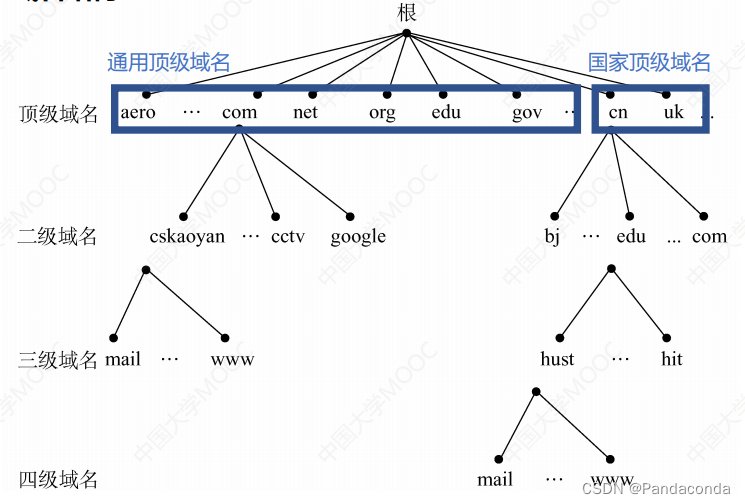
两种查询方式:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bJQyJVvY-1676336471042)(计网笔记.assets/image-20221214214837863.png)]](https://img-blog.csdnimg.cn/55d486e3cb47415f93524967d38ca9fb.png)
考点: 大题可能会考具体的实现过程。
3. FTP协议
FTP是基于客户/服务器(C/S)的协议。
用户通过一个客户机程序连接至在远程计算机上运行的服务器程序。
依照FTP 协议提供服务,进行文件传送的计算机就是FTP 服务器。
连接FTP服务器,遵循FTP协议与服务器传送文件的电脑就是FTP客户端。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DQzbGETm-1676336471044)(计网笔记.assets/image-20221214215445949.png)]](https://img-blog.csdnimg.cn/8b1791a5798d4753a1c16c25edf8a83e.png)
TFTP: 是TCP/IP协议族中的一个用来在客户机与服务器之间进行简单文件传输的协议,提供不复杂、开销不大的文件传输服务。端口号为69。
4. 电子邮件
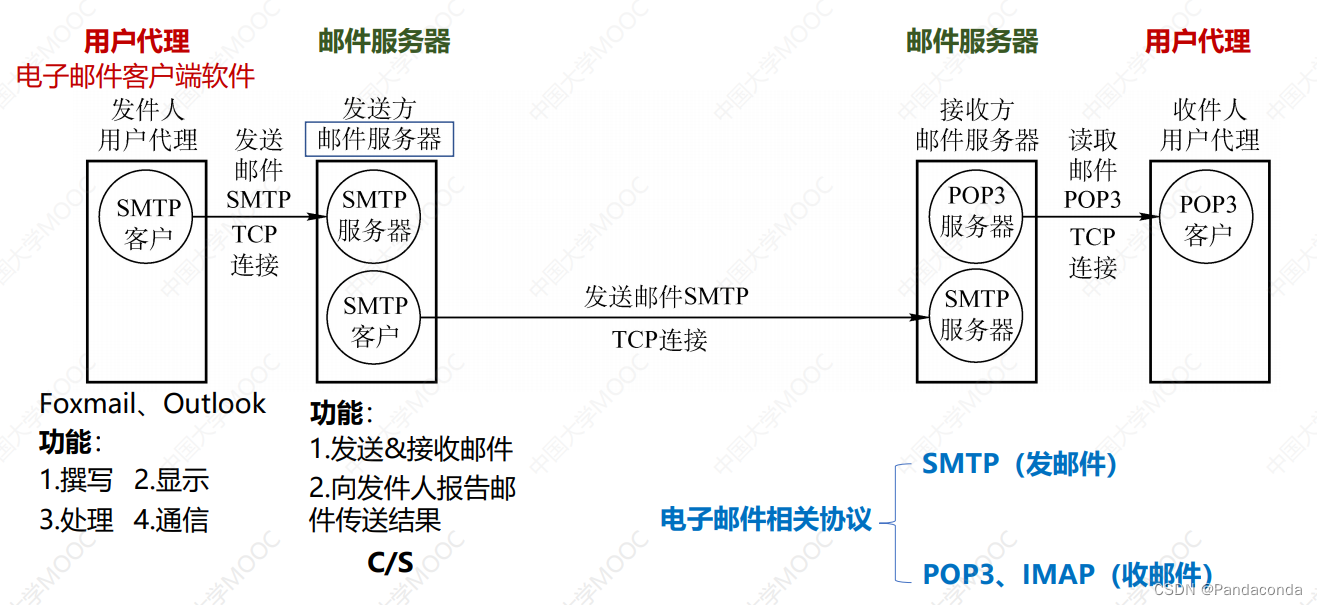
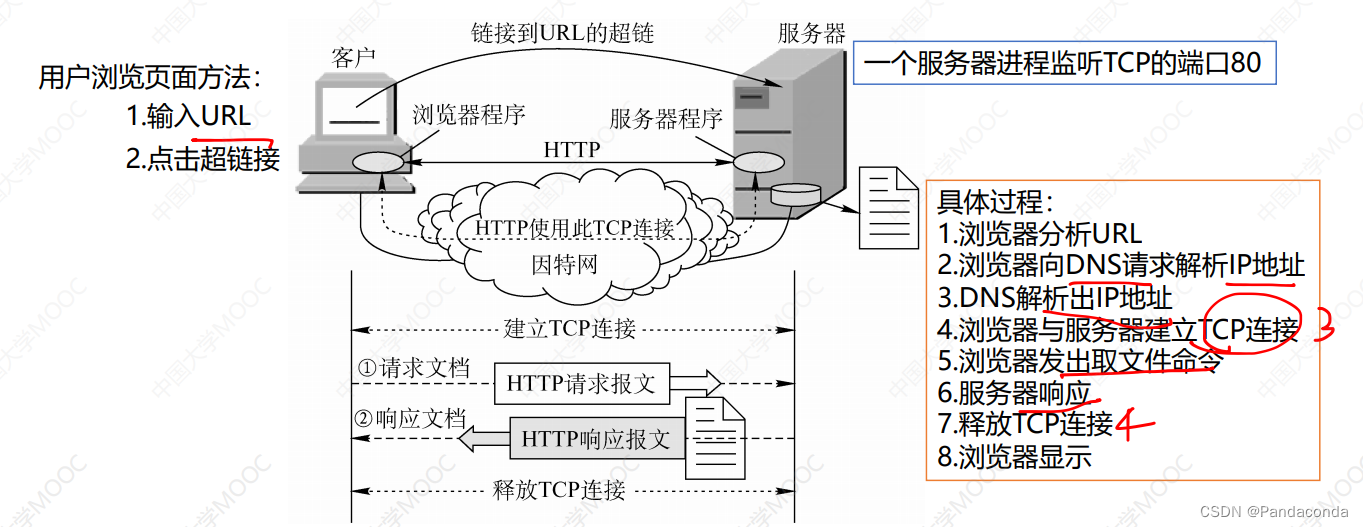
5. 万维网和HTTP协议
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v7uXTpPM-1676336471046)(计网笔记.assets/image-20221214215755085.png)]](https://img-blog.csdnimg.cn/bdb84016826841b0bb9dc8a7019fffc2.png)
HTTP协议定义了浏览器(万维网客户进程)怎样向万维网服务器请求万维网文档,以及服务器怎样把文档传送给浏览器。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M3jHCBiK-1676336471048)(计网笔记.assets/image-20221214215818417.png)]](https://img-blog.csdnimg.cn/6df0445199c84fc1b1a669c11c4ad65f.png)
考点: 大题可能会让你简单描述一下具体过程。
相关文章:
【计算机网络期末复习】第六章 应用层
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📣专栏定位:为想复习学校计算机网络课程的同学提供重点大纲,帮助大家渡过期末考~ 📚专栏地址:https://blog.csdn.net/Newin2020/arti…...

TypeScript基本教程
TS是JS的超集,所以JS基础的类型都包含在内 起步安装 npm install typescript -g运行tsc 文件名 基础类型 Boolean、Number、String、null、undefined 以及 ES6 的 Symbol 和 ES10 的 BigInt。 1 字符串类型 字符串是使用string定义的 let a: string 123 //普…...

使用Windows API实现本地音频采集
Windows API提供了Winmm(Windows多媒体)库,其中包括了音频设备相关的函数,可以用来实现音频设备的枚举和测试。 下面是一个简单的示例代码,演示了如何使用Winmm库中的waveInGetNumDevs()函数来枚举计算机上的音频输入…...

实用的费曼学习法 | 一些思考
文章目录 一、前言二、费曼学习法CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 大数据与人工智能背景下,最重要的是:捕捉机会和快速学习的能力 一、前言 费曼学习法是美国著名的物理学家,理查德 ∙ \bullet ∙ 费曼总结出来的学习方法。 这个方法的核心是:当你学习了…...

Linux安装Docker配置docker-compose 编排工具【超详细】
一、介绍Docker Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Linux或Windows操作系统的机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有…...

iTerm2 + Oh My Zsh 打造舒适终端体验
最终效果图: 因为powerline以及homebrew均需要安装command line tool,网络条件优越的同学在执行本文下面内容之前,可以先安装XCode并打开运行一次(会初始化安装components),省去以后在iterm2中的等待时间。…...
和dia_matrix()的区别)
【scipy.sparse】diags()和dia_matrix()的区别
【scipy.sparse】diags()和dia_matrix()的区别 文章目录【scipy.sparse】diags()和dia_matrix()的区别1. 介绍2. 代码示例2.1 sp.diags()2.1.1 第一种用法(dataoffsets)2.1.2 广播(需要指定shape)2.1.3 只有一条对角线2.2 sp.dia_…...
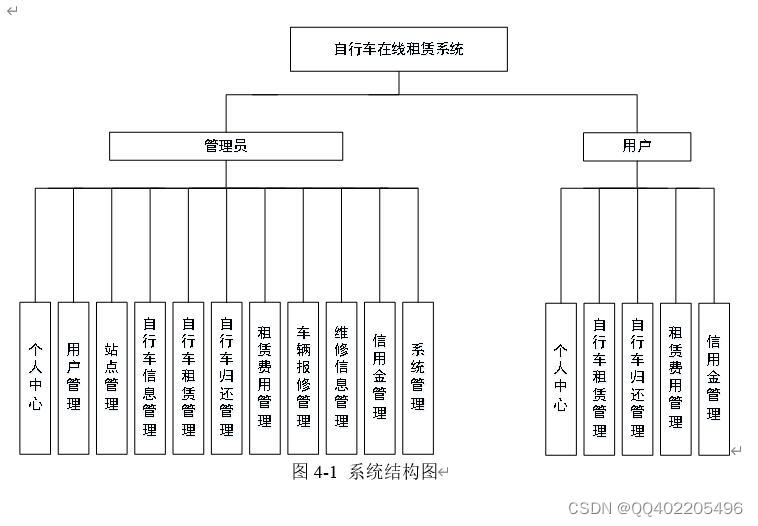
java ssm自行车在线租赁系统idea
当前自行车在社会上广泛使用,但自行车的短距离仍旧不能完全满足广大用户的需求。自行车在线租赁系统可以为用户提供租赁用车等功能,拥有较好的用户体验.能实时在线租赁提供更加快捷方便的租车方式,解决了常见自行车在线租赁系统较为局限的自行车归还功能。 通过使用本系统&…...

GAN和CycleGAN
文章目录1. GAN 《Generative Adversarial Nets》1.1 相关概念1.2 公式理解1.3 图片理解1.4 熵、交叉熵、KL散度、JS散度1.5 其他相关(正在补充!)2. Cycle GAN 《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Ne…...
源码项目中常见设计模式及实现
原文https://mp.weixin.qq.com/s/K8yesHkTCerRhS0HfB0LeA 单例模式 单例模式是指一个类在一个进程中只有一个实例对象(但也不一定,比如Spring中的Bean的单例是指在一个容器中是单例的) 单例模式创建分为饿汉式和懒汉式,总共大概…...
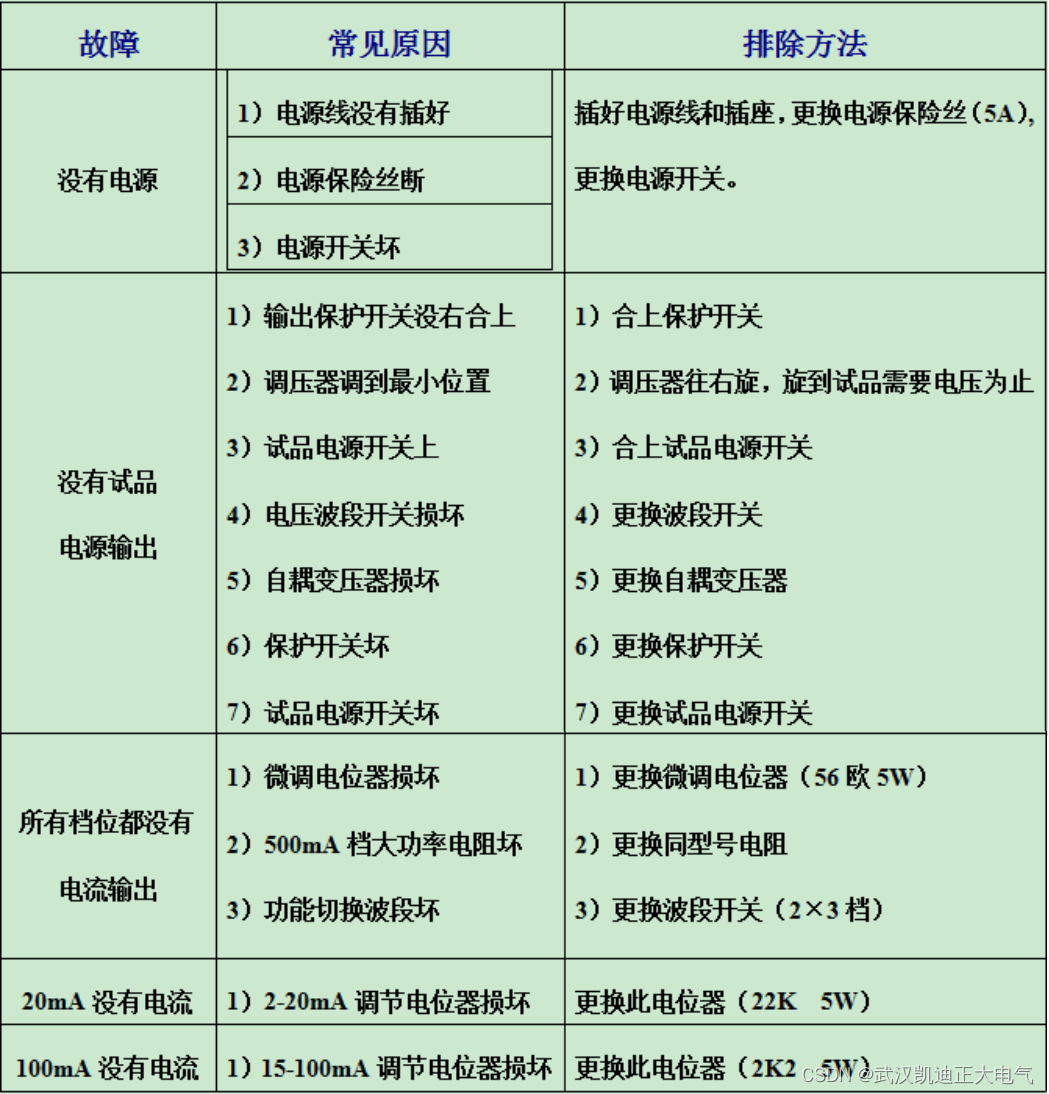
KDNM5000-10A-2剩余电流保护器测试仪
一、产品概述 KDNM5000-10A-2型剩余电流保护器测试仪(以下简称测试仪),是本公司改进产品,是符合国家标准《剩余电流动作保护器》(GB6829—95)中第8.3条和GB16917.1—1997中第9.9条验证AC型交流脱扣器动作特性要求的专用测试仪器。…...

C++实现线程池
C实现线程池一、前言二、线程池的接口设计2.1、类封装2.2、线程池的初始化2.3、线程池的启动2.4、线程池的停止2.5、线程的执行函数run()2.6、任务的运行函数2.7、等待所有线程结束三、测试线程池四、源码地址总结一、前言 C实现的线程池,可能涉及以下知识点&#…...
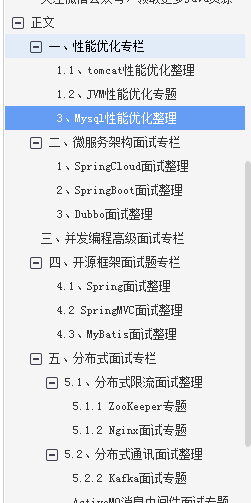
2023最新Java面试手册(性能优化+微服务架构+并发编程+开源框架)
Java面试手册 一、性能优化面试专栏 1.1、 tomcat性能优化整理 1.2、JVM性能优化整理 1.3、Mysql性能优化整理 二、微服务架构面试专栏 2.1、SpringCloud面试整理 2.2、SpringBoot面试整理 2.3、Dubbo面试整理 三、并发编程高级面试专栏 四、开源框架面试题专栏 4.1、Sprin…...

对灵敏度分析技术进行建模(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
完整爬虫学习笔记(第一章)
文章目录前言:fu:. 爬虫概述:hotdog:原理解剖:one: 服务器渲染:two: 前端JS渲染:fire: 第一个爬虫程序案例总结前言 最近正在学习Python网络爬虫的相关知识,鉴于本人Python水平有限 , 对Python并无太深的理解,所以此文章的主要目的在于抛砖引玉…...
会计师项目管理软件是什么,哪些必不可少的功能
欢迎阅读现代金融专业人士的会计师项目管理指南。在本文中,我们将深入探讨在基于项目的会计的各个方面使用项目管理方法的好处。我们还将教您面临哪些挑战以及如何为您的团队选择最佳工具。 为什么会计师的项目管理很重要? 在会计方面,目标始…...

第 8 章 优化
目录 8.1 优化概述 8.2 优化 SQL 语句 8.3 优化和指标 8.4 优化数据库结构 8.5 优化 InnoDB 表 8.6 优化 MyISAM 表 8.7 内存表的优化 8.8 了解查询执行计划 8.9 控制查询优化器 8.10 缓冲和缓存 8.11 优化锁定操作 8.12 优化 MySQL 服务器 8.13 衡量性能ÿ…...

剑指offer -- java题解
剑指offer -- java题解刷题地址1、数字在升序数组中出现的次数2、二叉搜索树的第k个节点3、二叉树的深度4、数组中只出现一次的两个数字5、和为S的两个数字6、左旋转字符串7、滑动窗口的最大值8、扑克牌顺子9、孩子们的游戏(圆圈中最后剩下的数)10、买卖股票的最好时机(一)刷题…...

若依ruoyi——手把手教你制作自己的管理系统【二、修改样式】
阿里图标一( ̄︶ ̄*)) 图片白嫖一((* ̄3 ̄)╭ ********* 专栏略长 爆肝万字 细节狂魔 请准备好一键三连 ********* 运行成功后: idea后台正常先挂着 我习惯用VScode操作 当然如果有两台机子 一个挂后台一个改前端就更好…...

2023.2.14每日一题——455. 分发饼干
每日一题题目描述解题核心解法一:双指针题目描述 题目链接:455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
