AtCoder Regular Contest 137 题解(A~C)
A-Coprime Pair
思路
我们知道两个质数之间并不会相隔太远,于是我们直接用暴力就可以通过这题。
先从大到小枚举答案,并且枚举所有可能的起点,当枚举到的两个值满足条件输出并结束程序即可。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL x, y, ans;
LL gcd(LL a, LL b) { return b == 0 ? a : gcd(b, a % b); }
int main() {scanf("%lld%lld", &x, &y);for (LL i = y - x; i; i--) {for (LL j = x; j + i <= y; j++) {if (gcd(j, j + i) == 1) {printf("%d", i);return 0;}}}return 0;
}
B-Count 1’s
思路
假设我们所能得到的分数的最大值为 ansmaxansmaxansmax ,最小值为 ansminansminansmin ,则答案一定为 max−min+1max - min + 1max−min+1 ,因为每次多改变一个节点,所能取到的分数只会改变一,在整数情况下看他是连续的。
再稍微转换一下,就会发现,其实也就是求变换之后所能对原分数产生的改变的最大值和最小值的差。
于是我们将问题变为了如何求改变的最大值和最小值。
我们先将原数组按一下方式处理:
- 如果 aia_iai 为 111 ,则将 bib_ibi 设为 −1-1−1
- 如果 aia_iai 为 000 ,则将 bib_ibi 设为 111
此时的 bbb 数组记录的就是如果改变这个节点,会对当前分数产生的影响。
我们再将 bbb 数组取一个前缀和,此时 bbb 数组表示的就是从第一个节点到这个节点全部改变对分数产生的影响。
我们记录一个从起点开始改变,所能得到分数的最大值为 maxnmaxnmaxn ,最小值为 minnminnminn 。
我们从一开始枚举,对于每个节点,我们都将 ansmaxansmaxansmax 和 ansminansminansmin 更新一下,然后更新一下 maxnmaxnmaxn 和 minnminnminn 就可以了。
更新方式看代码。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, a[300005], b[300005], maxn, minn, ansmax, ansmin;
int main() {scanf("%d", &n);for (int i = 1; i <= n; i++)scanf("%d", &a[i]), b[i] = b[i - 1] + (a[i] == 0 ? 1 : -1);for (int i = 1; i <= n; i++) {ansmax = max(ansmax, b[i] - minn);//b[i]-minn就是以当前节点为结尾所能产生的最大值ansmin = min(ansmin, b[i] - maxn);//b[i]-maxn就是以当前节点为结尾所能产生的最小值maxn = max(maxn, b[i]);minn = min(minn, b[i]);}printf("%d", ansmax - ansmin + 1);return 0;
}
C-Distinct Numbers
思路
我们先看最大两个点。
然后我们分情况讨论。
首先假设两个点之间的距离超过 111 ,此时如果我们将最大值移到次大值加一的位置后,我们必赢,则就移过去。
如果我们必输呢?
因为我们移到次大值加一后,对方必须移到前面一个空位处,我们假设对方移到一个点 aaa 后我们必输,则我们第一次移动就不移到次大值加一,直接移到点 aaa ,此时的局面和我们移到次大值加一的位置然后对方再移到点 aaa 是一样的,因为这个局面先手的人必败,所以我们移到点 aaa 后对方必败。
通过上面两种情况,我们知道如果最大值和次大值之间的差大于一,则无论如何先手必胜。
我们再看看最大值和次大值之间的差等于一的时候。
因为如果我们移到一个位置使得移完后这个节点到最大值之间有空格,此时就会回到我们先前讨论的情况,这是对方是必胜的。
于是我们和对方的每次移动都得要移到前面离最大值最近的空格。
于是我们可以根据空格数来判断谁赢。
如果空格数是偶数,则最后一下是对方移动,那我们必输。
如果空格数是奇数,则最后一下是我们移动,那我们必赢。
于是我们就可以做这道题了。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, m, a[3000005];
int main() {scanf("%d", &n);for (int i = 1; i <= n; i++) scanf("%d", &a[i]);if (a[n] - a[n - 1] > 1)printf("Alice");else {if ((a[n] - n) % 2)//a[n]-n就相当于空格数printf("Bob");elseprintf("Alice");}return 0;
}
相关文章:
)
AtCoder Regular Contest 137 题解(A~C)
A-Coprime Pair 思路 我们知道两个质数之间并不会相隔太远,于是我们直接用暴力就可以通过这题。 先从大到小枚举答案,并且枚举所有可能的起点,当枚举到的两个值满足条件输出并结束程序即可。 代码 #include <bits/stdc.h> using n…...

【C语言】预处理指令
C语言预处理指令一、什么是预处理指令二、预处理指令特点三、文件包含四、C标准库<stdio.h>一、什么是预处理指令 C语言的源文件(.c文件)需要经过编译生成可执行程序,编译操作会将源文件转换成目标文件,对于 VC、VS&#x…...

Java基础之多线程JUC全面学习笔记
目录初识多线程多线程的实现方式常见的成员方法线程安全的问题死锁生产者和消费者线程池自定义线程池初识多线程 什么是多线程? 线程 线程是操作系统能够进行运算调度的最小单位。线程被包含在进程之中,是进程中的实际运作单位。 简单理解:应用软件中互相独立&…...

13.CSS文本样式
文本样式 h1 {color: blue; }● 回顾上一节的内容,我们让h1标题的文字变成了蓝色,注意如果html中有多个h1标签,那我们这种写法所有的h1标签都会变成蓝色,除了颜色,本节我们将学习更多的CSS属性 文字大小font-size h…...

西恩科技更新招股书:IPO前大手笔分红“套现”, 赵志安为实控人
2月14日,上海西恩科技股份有限公司(下称“西恩科技”)更新了招股书(申报稿)。据贝多财经了解,西恩科技于2022年8月12日递交上市申请材料,准备在创业板上市,此次是西恩科技第二次更新…...
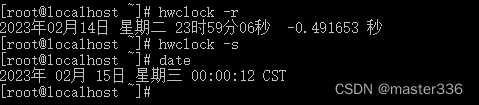
【CentOS】有关时间的设置
目录环境信息date语法信息查看时间设置时间设置日期tzselecttimedatectl语法显示当前及所有时区修改时区hwclock语法读取硬件时钟使用硬件时钟设置系统时间使用系统时间设置硬件时钟如何理解硬件时钟和系统时钟环境信息 CentOS 7 date 语法信息 date --help用法:…...

OpenCV制作Mask图像掩码
一、掩膜(mask) 在有些图像处理的函数中有的参数里面会有mask参数,即此函数支持掩膜操作,首先何为掩膜以及有什么用,如下: 数字图像处理中的掩膜的概念是借鉴于PCB制版的过程,在半导体制造中&am…...
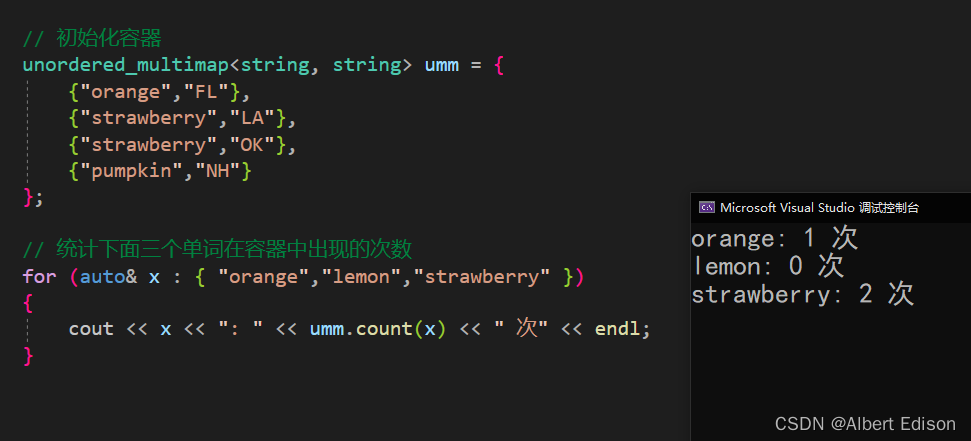
C++STL剖析(九)—— unordered_map和unordered_multimap的概念和使用
文章目录1. unordered_map的介绍和使用🍑 unordered_map的构造🍑 unordered_map的使用🍅 insert🍅 operator[ ]🍅 find🍅 erase🍅 size🍅 empty🍅 clear🍅 sw…...

Android无菜单键,如何触发onCreateOptionsMenu(Menu menu)
文章目录小结问题及解决无法触发onCreateOptionsMenu(Menu menu)修改配置文件解决使用一个按钮来触发其它办法参考小结 现在的Android有三个键: 任务键,Home键,返回键,也就是没有菜单键了,那么如何如何触发onCreateOp…...

“黑洞”竟是外星人的量子计算机?
宇宙中的黑洞可以用作终极量子计算机,我们可以从中探索它们的特征。(图片来源:网络)我们完全有理由怀疑生命在我们的宇宙中很常见,但是为什么我们从未发现过其他生命存在的迹象?这个问题几乎自现代天文学诞…...

计算机网络入门
一,计算机网络在信息时代中的作用 21世纪的一些重要特征就是数字化,网络化和信息化,它是一个以网络为核心的信息时代。有三类大家很熟悉的网络,即电信网络,有线电视网络和计算机网络。按照最初的服务分工,…...
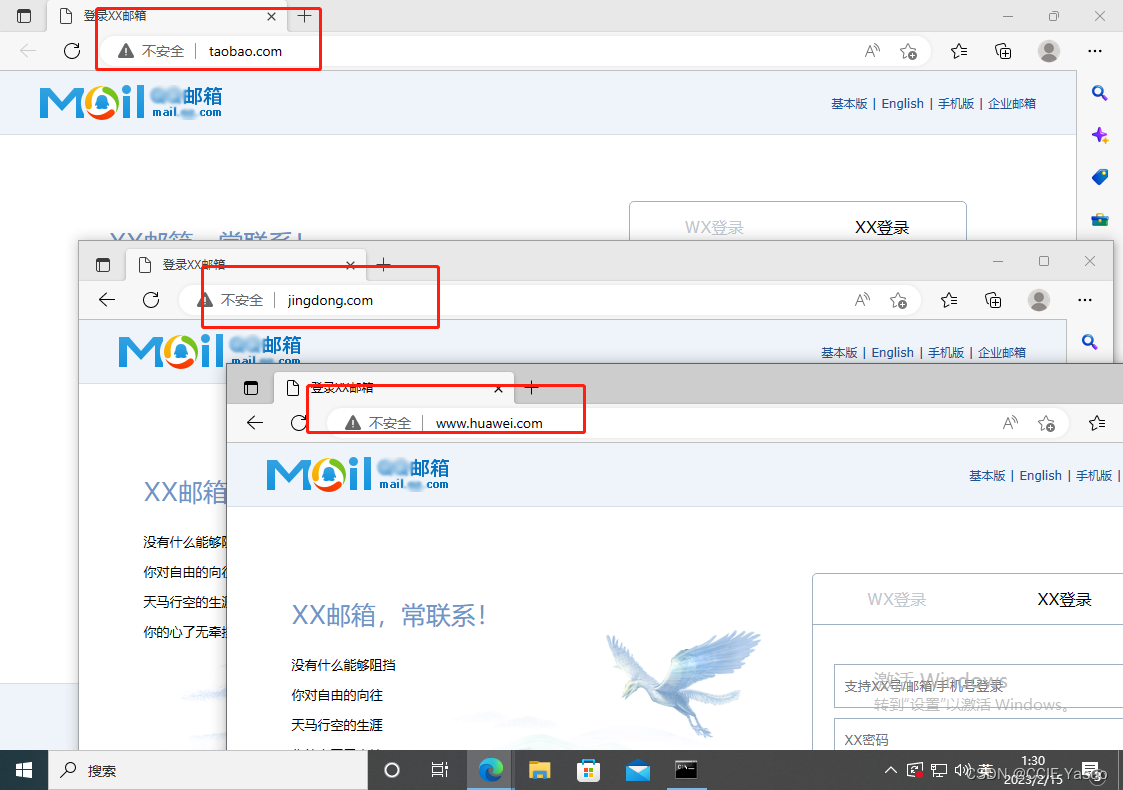
网络安全-内网DNS劫持-ettercap
网络安全-内网DNS劫持-ettercap 前言 一,我也是初学者记录的笔记 二,可能有错误的地方,请谨慎 三,欢迎各路大神指教 四,任何文章仅作为学习使用 五,学习网络安全知识请勿适用于违法行为 学习网络安全知识请…...

synchronized和Lock的区别
synchronized和lock的区别 synchronized和Lock,我已经通过源码级别的介绍过了,下面我们来总结下他们的区别 区别: 1.synchronized是关键字,Lock是接口,synchronized是JVM层实现,Lock是JDK中JUC包下的实现;…...

SpringBoot 指标监控 Actuator
Spring Boot Actuator为 Micrometer 提供了依赖管理和自动配置,Micrometer是一个支持 众多监控系统 的应用程序指标接口 该功能与:java\jdk\bin 下的 Jconsole 功能雷同 1、pom文件中引入依赖(使用的springboot是2.7.2) <dep…...

面试浅谈之十大排序算法
面试浅谈之十大排序算法 HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是面试浅谈系列,收录在专栏面试中 😜😜😜 本系列将记录一些阿呆个人整理的面试题 🏃&…...

LeetCode-1250. 检查「好数组」【数论,裴蜀定理】
LeetCode-1250. 检查「好数组」【数论,裴蜀定理】题目描述:解题思路一:裴蜀定理是:a*xb*y1。其中a,b是数组中的数,x,y是任意整数。如果a,b互质那么一定有解。问题即转换为寻找互质的数。解题思路二:简化代码…...

【Linux】NTP时间同步服务与NFS网络文件共享存储服务器(配置、测试)
一、NTP时间同步服务1、NTP介绍NTP服务器【Network Time Protocol(NTP)】是用来使计算机时间同步化的一种协议,它可以使计机对其服务器或时钟源(如石英钟,GPS等等)做同步化,它可以提供高精准度的时间校正&a…...
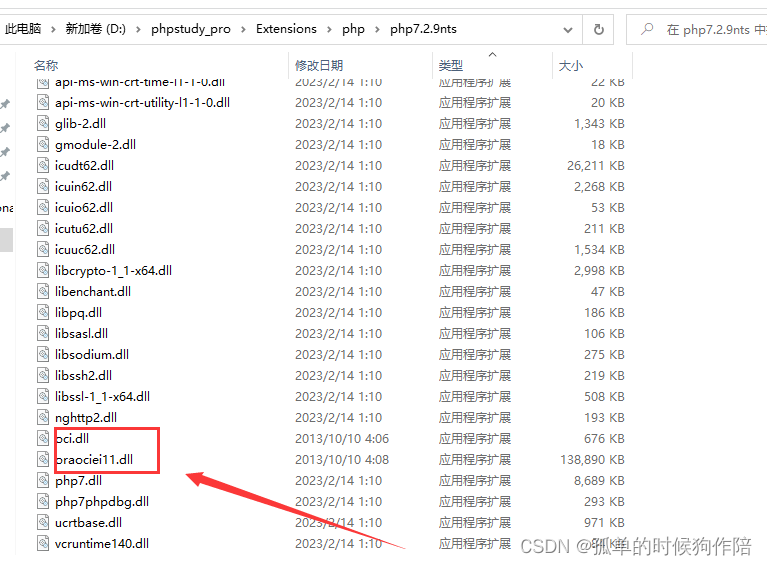
windows下php连接oracle安装oci8扩展报错(PHP Startup: Unable to load dynamic library ‘oci8_11g‘)
记录一下php7.29安装oci8的艰苦过程,简直就是唐僧西天取经历经九九八十一难。 使用的是phpstudy_pro安装的ph扩展wnmp环境下; 1 、安装oralce Instant Client 首先,安装oci8和pdo_oci扩展依赖的Oracle client。了解到需要连接的Oracle版…...

TensorRT的功能
TensorRT的功能 文章目录TensorRT的功能2.1. C and Python APIs2.2. The Programming Model2.2.2. The Runtime Phase2.3. Plugins2.4. Types and Precision2.5. Quantization2.6. Tensors and Data Formats2.7. Dynamic Shapes2.8. DLA2.9. Updating Weights2.10. trtexec本章…...
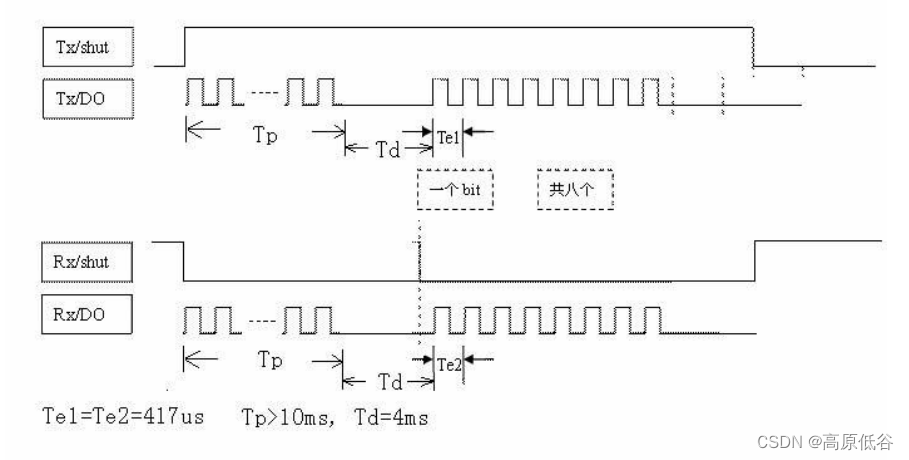
433MHz无线通信--模块RXB90
1、接收模块RXB90简介 两个数据输出是联通的。 2、自定义一个编码解码规则 组数据为“0x88 0x03 0xBD 0xB6”。 3、发射模块 如何使用示波器得到捕捉一个周期的图像? 通过date引脚连接示波器CH1,以及示波器探针的接地端接芯片的GND,分…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
