LeetCode-1250. 检查「好数组」【数论,裴蜀定理】
LeetCode-1250. 检查「好数组」【数论,裴蜀定理】
- 题目描述:
- 解题思路一:裴蜀定理是:a*x+b*y=1。其中a,b是数组中的数,x,y是任意整数。如果a,b互质那么一定有解。问题即转换为寻找互质的数。
- 解题思路二:简化代码1
- 解题思路三:三行代码!
题目描述:
给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。
假如该和结果为 1,那么原数组就是一个「好数组」,则返回 True;否则请返回 False。
示例 1:
输入:nums = [12,5,7,23]
输出:true
解释:挑选数字 5 和 7。
53 + 7(-2) = 1
示例 2:
输入:nums = [29,6,10]
输出:true
解释:挑选数字 29, 6 和 10。
291 + 6(-3) + 10*(-1) = 1
示例 3:
输入:nums = [3,6]
输出:false
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
https://leetcode.cn/problems/check-if-it-is-a-good-array/description/
解题思路一:裴蜀定理是:ax+by=1。其中a,b是数组中的数,x,y是任意整数。如果a,b互质那么一定有解。问题即转换为寻找互质的数。
class Solution {
public:bool isGoodArray(vector<int>& nums) {int s=0;for (int x : nums) {s=gcd(x,s);if(s==1) return true;//剪枝}return s==1;}int gcd(int a, int b) {//辗转相除法if(b==0) return a;return gcd(b,a%b);}
};
时间复杂度:O(n)
空间复杂度:O(1)
解题思路二:简化代码1
class Solution {
public:bool isGoodArray(vector<int>& nums) {int s=0;for (int x : nums) {s=gcd(x,s);if(s==1) return true;//剪枝}return s==1;}
};
时间复杂度:O(n)
空间复杂度:O(1)
解题思路三:三行代码!
class Solution {
public:bool isGoodArray(vector<int>& nums) {int s=0;for (int x : nums) s=gcd(x,s);return s==1;}
};
时间复杂度:O(n)
空间复杂度:O(1)
相关文章:

LeetCode-1250. 检查「好数组」【数论,裴蜀定理】
LeetCode-1250. 检查「好数组」【数论,裴蜀定理】题目描述:解题思路一:裴蜀定理是:a*xb*y1。其中a,b是数组中的数,x,y是任意整数。如果a,b互质那么一定有解。问题即转换为寻找互质的数。解题思路二:简化代码…...

【Linux】NTP时间同步服务与NFS网络文件共享存储服务器(配置、测试)
一、NTP时间同步服务1、NTP介绍NTP服务器【Network Time Protocol(NTP)】是用来使计算机时间同步化的一种协议,它可以使计机对其服务器或时钟源(如石英钟,GPS等等)做同步化,它可以提供高精准度的时间校正&a…...
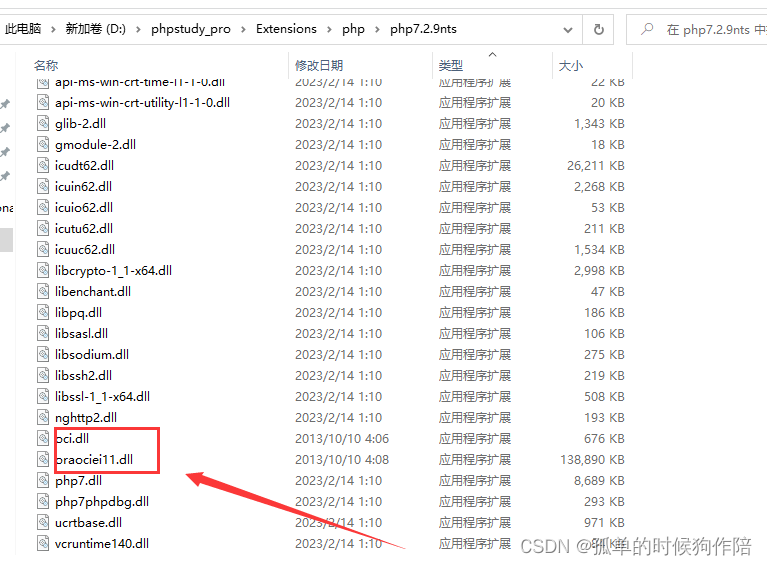
windows下php连接oracle安装oci8扩展报错(PHP Startup: Unable to load dynamic library ‘oci8_11g‘)
记录一下php7.29安装oci8的艰苦过程,简直就是唐僧西天取经历经九九八十一难。 使用的是phpstudy_pro安装的ph扩展wnmp环境下; 1 、安装oralce Instant Client 首先,安装oci8和pdo_oci扩展依赖的Oracle client。了解到需要连接的Oracle版…...

TensorRT的功能
TensorRT的功能 文章目录TensorRT的功能2.1. C and Python APIs2.2. The Programming Model2.2.2. The Runtime Phase2.3. Plugins2.4. Types and Precision2.5. Quantization2.6. Tensors and Data Formats2.7. Dynamic Shapes2.8. DLA2.9. Updating Weights2.10. trtexec本章…...
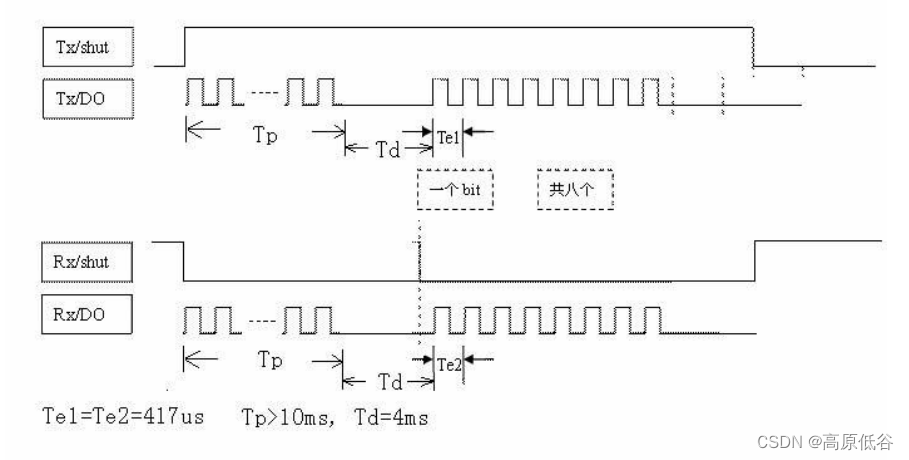
433MHz无线通信--模块RXB90
1、接收模块RXB90简介 两个数据输出是联通的。 2、自定义一个编码解码规则 组数据为“0x88 0x03 0xBD 0xB6”。 3、发射模块 如何使用示波器得到捕捉一个周期的图像? 通过date引脚连接示波器CH1,以及示波器探针的接地端接芯片的GND,分…...
-2PC核心源码解读)
Seata源码学习(三)-2PC核心源码解读
Seata源码分析-2PC核心源码解读 2PC提交源码流程 上节课我们分析到了GlobalTransactionalInterceptor全局事务拦截器,一旦执行拦截器,我们就会进入到其中的invoke方法,在这其中会做一些GlobalTransactional注解的判断,如果有注解…...

IO流概述
🏡个人主页 : 守夜人st 🚀系列专栏:Java …持续更新中敬请关注… 🙉博主简介:软件工程专业,在校学生,写博客是为了总结回顾一些所学知识点 目录IO流概述IO 流的分类总结流的四大类字…...

【node.js】node.js的安装和配置
文章目录前言下载和安装Path环境变量测试推荐插件总结前言 Node.js是一个在服务器端可以解析和执行JavaScript代码的运行环境,也可以说是一个运行时平台,仍然使用JavaScript作为开发语言,但是提供了一些功能性的API。 下载和安装 Node.js的官…...

Python优化算法—遗传算法
Python优化算法—遗传算法一、前言二、安装三、遗传算法3.1 自定义函数3.2 遗传算法进行整数规划3.3 遗传算法用于旅行商问题3.4 使用遗传算法进行曲线拟合一、前言 优化算法,尤其是启发式的仿生智能算法在最近很火,它适用于解决管理学,运筹…...
的应用价值剖析)
数据埋点(Data buried point)的应用价值剖析
一、什么是数据埋点?数据埋点指在应用中特定的流程中收集一些信息,用来跟踪应用使用的状况,后续用来进一步优化产品或是提供运营的数据支撑。比如访问数(Visits),访客数(Visitor),停…...

一文弄懂硬链接、软链接、复制的区别
复制 命令:cp file1 file2 作用:实现对file1的一个拷贝。 限制:可以跨分区,文件夹有效。 效果:修改file1,对file2无影响;修改file2,对file1无影响。删除file1,对file…...
界面组件Telerik ThemeBuilder R1 2023开创应用主题研发新方式!
Telerik DevCraft包含一个完整的产品栈来构建您下一个Web、移动和桌面应用程序。它使用HTML和每个.NET平台的UI库,加快开发速度。Telerik DevCraft提供最完整的工具箱,用于构建现代和面向未来的业务应用程序,目前提供UI for ASP.NET包含一个完…...

在FederatedScope 如何查看clientserver之间的传递的参数大小(通讯量)? 对源码的探索记录
在FederatedScope 如何查看client/server之间的传递的参数大小(通讯量)? 对源码的探索记录 背景需求 想给自己的论文补一个通讯开销对比实验:需要计算出client和server之间传递的信息(例如,模型权重、embedding)总共…...

2023爱分析 · 数据科学与机器学习平台厂商全景报告 | 爱分析报告
报告编委 黄勇 爱分析合伙人&首席分析师 孟晨静 爱分析分析师 目录 1. 研究范围定义 2. 厂商全景地图 3. 市场分析与厂商评估 4. 入选厂商列表 1. 研究范围定义 研究范围 经济新常态下,如何对海量数据进行分析挖掘以支撑敏捷决策、适应市场的快…...

20230215_数据库过程_高质量发展
高质量发展 —一、运营结果 SQL_STRING:‘delete shzc.np_rec_lnpdb a where exists (select * from tbcs.v_np_rec_lnpdbbcv t where a.telnumt.telnum and a.outcarriert.OUTCARRIER and a.incarriert.INCARRIER and a.owncarriert.OWNCARRIER and a.starttimet.STARTTIME …...

【百度 JavaScript API v3.0】LocalSearch 位置检索、Autocomplete 结果提示
地名检索移动到指定坐标 需求 在输入框中搜索,在下拉列表中浮动,右侧出现高亮的列表集。选中之后移动到指定坐标。 技术点 官网地址: JavaScript API - 快速入门 | 百度地图API SDK 开发文档:百度地图JSAPI 3.0类参考 实现 …...

运用Facebook投放,如何制定有效的竞价策略?
广告投放中,我们经常会遇到一个问题,就是不知道什么样的广告适合自己的业务。其实,最简单的方法就是根据我们业务本身进行定位并进行投放。当你了解了广告主所处行业及目标受众后,接下来会针对目标市场进行搜索和定位(…...

大数据框架之Hadoop:HDFS(五)NameNode和SecondaryNameNode(面试开发重点)
5.1NN和2NN工作机制 5.1.1思考:NameNode中的元数据是存储在哪里的? 首先,我们做个假设,如果存储在NameNode节点的磁盘中,因为经常需要进行随机访问,还有响应客户请求,必然是效率过低。因此&am…...

计算机网络 - 1. 体系结构
目录概念、功能、组成、分类概念功能组成分类分层结构概念总结OSI 七层模型应用层表示层会话层传输层网络层数据链路层物理层TCP/IP 四层模型OSI 与 TCP/IP 相同点OSI 与 TCP/IP 不同点为什么 TCP/IP 去除了表示层和会话层五层参考模型概念、功能、组成、分类 概念 …...

银行业上云进行时,OLAP 云服务如何解决传统数仓之痛?
本文节选自《中国金融科技发展概览:创新与应用前沿》,从某国有大行构建大数据云平台的实践出发,解读了 OLAP 云服务如何助力银行实现技术平台化、组件化和云服务化,降低技术应用门槛,赋能业务创新。此外,本…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...
