面试浅谈之十大排序算法
面试浅谈之十大排序算法
HELLO,各位博友好,我是阿呆 🙈🙈🙈
这里是面试浅谈系列,收录在专栏面试中 😜😜😜
本系列将记录一些阿呆个人整理的面试题 🏃🏃🏃
OK,兄弟们,废话不多直接开冲 🌞🌞🌞
一 🏠 概述
排序定义
对一序列对象根据某个关键字进行排序
术语
- 稳定:如果 a 在 b 前,且 a = b,排序后 a 仍在 b 前
- 不稳定:如果 a 在 b 前,且 a = b,排序后 a 可能在 b 后
- 内排序:所有排序操作在内存中完成
- 外排序:数据太大,因此放在磁盘中,排序通过磁盘和内存数据传输进行
- 时间复杂度: 算法执行所耗费时间
- 空间复杂度:算法执行所耗费内存
算法总结
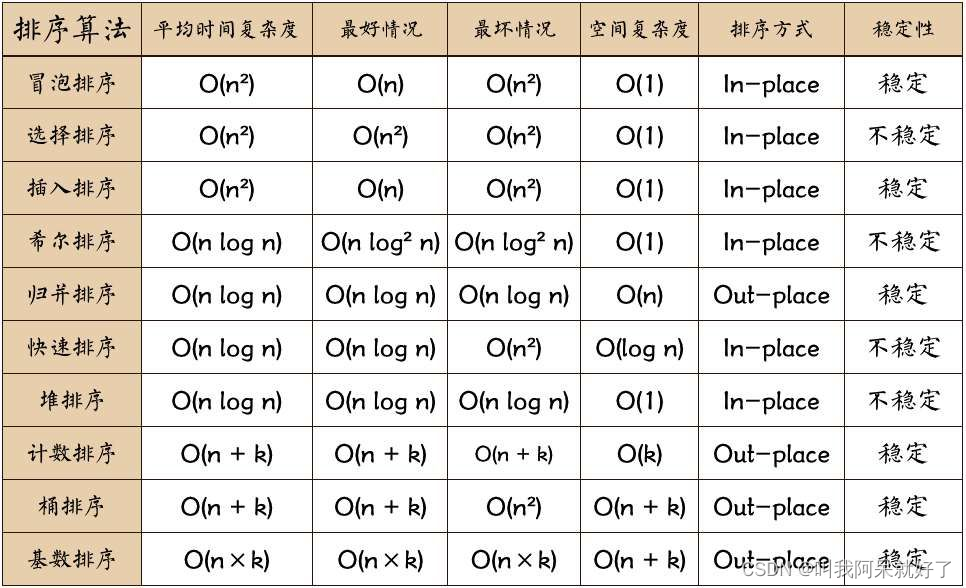
名词解释
- n : 数据规模
- k : 桶个数
- In-place : 占用常数内存,不占用额外内存
- Out-place : 占用额外内存
算法分类
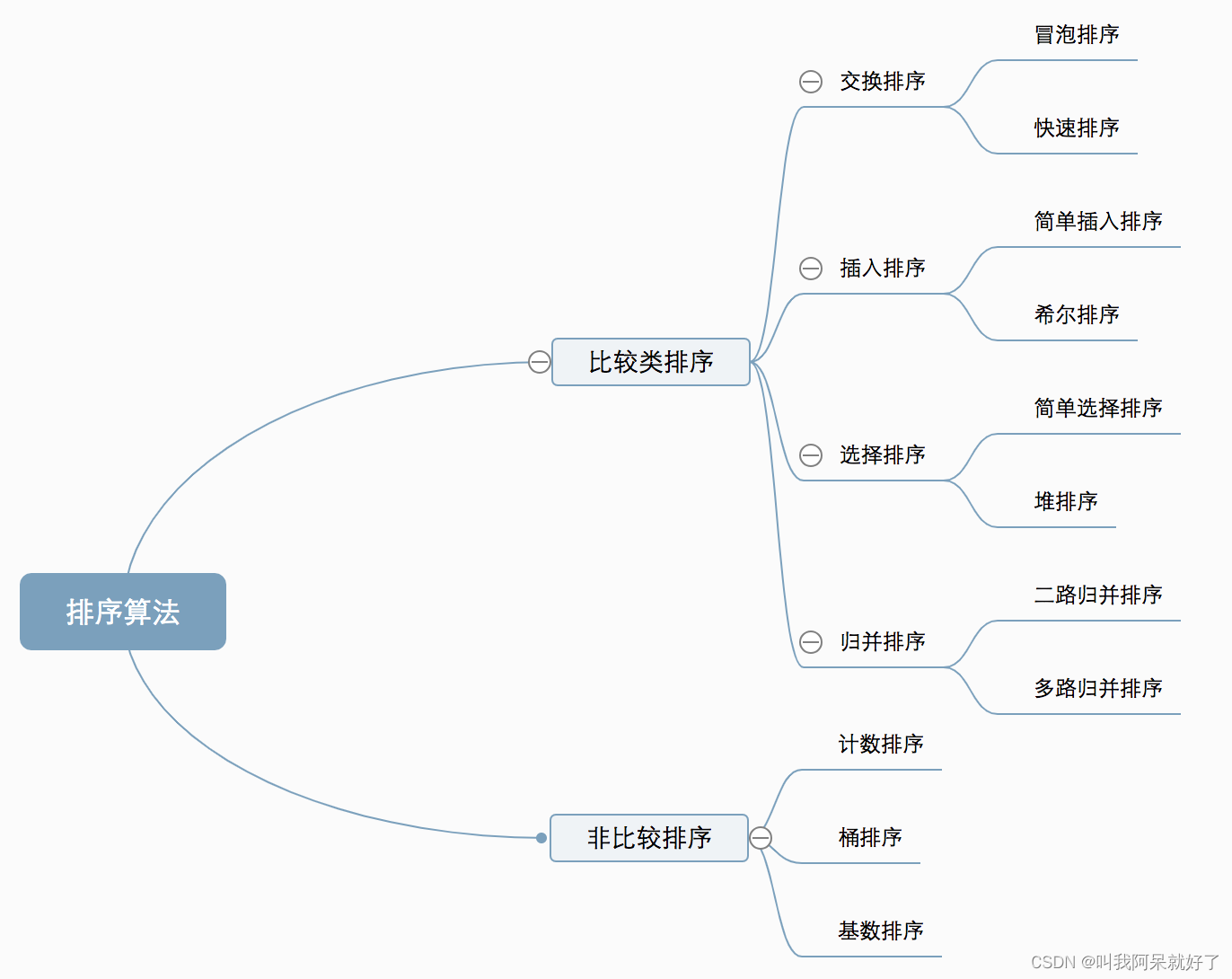
比较和非比较区别
常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较,才能确定自己的位置
在冒泡排序之类的排序中,问题规模为 n,又因为需要比较n次,所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中,问题规模通过分治法消减为logN次,所以时间复杂度平均O(nlogn)
比较排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况
计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置。非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)
非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求
二 🏠 核心
冒泡排序(Bubble Sort)
冒泡排序,重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来
算法描述
- 比较相邻的元素,如果第一个比第二个大,就交换它们两个
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数
- 针对所有的元素重复以上的步骤,除了最后一个
- 重复步骤1~3,直到排序完成
代码实现
// 两数交换
void mySwap(int &a, int &b) {int tmp = a;a = b;b = tmp;
}// 冒泡排序
void BubbleSort(vector<int> &num) {bool sortFlag; //某趟排序后已有序, 则不需要再空跑趟int len = num.size();for (int i = 0; i < len; ++i) {for (int j = 0; j < len - i - 1; ++j) {if (num[j + 1] < num[j])mySwap(num[j + 1], num[j]);}if (!sortFlag) return vec;}
}
选择排序(Selection Sort)
首先找到数组最小元素,将它和数组第一个元素交换位置。在剩下元素中找到最小元素,将它与数组第二个元素交换位置,如此往复,直至 n - 1 结束
算法描述
- 初始状态 :无序区为 R[1…n],有序区为空
- 第 i 趟排序 (i = 1, 2, 3 … n - 1) 开始时,当前有序区和无序区分别为R [1 … i - 1] 和 R (i … n)。该趟排序从当前无序区中选出关键字最小的记录 R[k],将它与无序区的第 1 个记录 R 交换,使 R[1 … i] 和 R[i+1 … n) 分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n - 1 趟结束,数组有序化了
代码实现
// 选择排序
void SelectionSort(vector<int> &num) {int len = num.size();for (int i = 0; i < len - 1; ++i) {int minPos = i;for (int j = i + 1; j < len; ++j) {if (num[j] < num[minPos])minPos = j;}mySwap(num[i], num[minPos]);}
}
算法分析
时间复杂度:O ( n 2 )
空间复杂度:O ( 1 )
稳定性:不稳定排序
直接插入排序(Insertion Sort)
把第一个元素作为有序部分,从第二个元素开始将剩余元素逐个插入有序部分的合适位置
算法描述
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
代码实现
// 直接插入排序
void InsertionSort(vector<int> &num) {int len = num.size();for (int i = 1; i < len; ++i) {int tmp = num[i];int j = i - 1;while (j >= 0 && num[j] > tmp) { //在找合适位置num[j + 1] = num[j]; //移动元素位置--j; //移动索引}num[j + 1] = tmp; //插入合适位置}
}
算法分析
时间复杂度:O ( n 2 )
空间复杂度:O ( 1 )
稳定性:稳定排序
希尔排序(Shell Sort)
希尔排序是简单插入排序改进后的版本
把记录按增量分组,对每组使用直接插入排序;当增量减至 1 时,整个文件恰被分成一组
算法描述
- 选择一个增量序列 t1,t2,…,tk,其中 ti > tj,tk = 1;
- 按增量序列个数 k,对序列进行 k 趟排序
- 每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
动图演示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AWdpSoyP-1676381476583)(https://cdn-1301239564.cos.ap-beijing.myqcloud.com/image/programming/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F.jpg)]](https://img-blog.csdnimg.cn/94489542f44840bb9d8c586d4fa93096.png)
代码实现
void ShellSort(vector<int> &num) {int len = num.size();// 逐渐缩小间隔,最终为1for (int step = len / 2; step > 0; step /= 2) {for (int i = step; i < len; ++i) {int tmp = num[i];int j = i - step;while (j >= 0 && tmp < num[j]) {num[j + step] = num[j];j -= step;}num[j + step] = tmp;}}
}
算法分析
时间复杂度:O ( n 2 )
空间复杂度:O ( 1 ) O(1)O(1)
稳定性:不稳定排序
归并排序(Merge Sort)
即先使子序列有序,再使子序列段间有序
算法描述
- 长度为 n 输入序列分成两个长度为 n/2 子序列
- 对两个子序列分别采用归并排序
- 将两个排序好子序列合并成一个最终序列
代码实现
void Merge(int *arr, int n) {int temp[n]; // 辅助数组int b = 0; // 辅助数组的起始位置int mid = n / 2; // mid将数组从中间划分,前一半有序,后一半有序int first = 0, second = mid; // 两个有序序列的起始位置while (first < mid && second < n) {if (arr[first] <= arr[second]) // 比较两个序列temp[b++] = arr[first++];elsetemp[b++] = arr[second++];}while(first < mid) temp[b++] = arr[first++]; // 将剩余子序列复制到辅助序列中 while(second < n) temp[b++] = arr[second++];for (int i = 0; i < n; ++i) // 辅助序列复制到原序列arr[i] = temp[i];
}void MergeSort(int *arr, int n) {if (n <= 1) return; // 递归出口if (n > 1) {MergeSort(arr, n / 2); // 对前半部分进行归并排序MergeSort(arr + n / 2, n - n / 2); // 对后半部分进行归并排序Merge(arr, n); // 归并两部分}
}
算法分析
时间复杂度:O ( n ∗ l o g n )
空间复杂度:O ( n )
稳定性:稳定排序
快速排序(Quick Sort)
从数组中选择一个元素,称为 基准。把数组中所有小于 基准 元素放左边,所有大于或等于 基准 元素放右边(此时 基准 元素位置有序,即无需再移动 基准 位置)
以 基准 为界把大数组切割成两个小数组(分割操作,partition),对 基准 左右两边数组进行递归操作,直到数组大小为1。此时每个元素都处于有序位置
算法描述
- 从数列中挑出一个元素,称为 基准(pivot)
- 重新排序数列,比基准值小在前,比基准值大在后
- 递归把小于基准值子数列和大于基准值子数列排序
代码实现
// 分割操作
int Partition(vector<int> &num, int left, int right) {int pivot = num[left];int i = left + 1, j = right;while (true) {// 向右找到第一个小于等于 pivot 的元素位置while (i <= j && num[i] <= pivot)++i;// 向左找到第一个大于等于 pivot 的元素位置while(i <= j && num[j] >= pivot ) --j;if(i >= j)break;// 交换两个元素的位置,使得左边的元素不大于pivot,右边的不小于pivotmySwap(num[i], num[j]);}// 使中轴元素处于有序的位置num[left] = num[j]; num[j] = pivot; //经过上面的循环, j 后面就全是大于或等于 pivot 的数return j;
}// 快速排序
void QuickSort(vector<int> &num, int left, int right) {if (left < right) {// 获取中轴元素所处的位置并进行分割int mid = Partition(num, left, right);// 递归处理QuickSort(num, left, mid - 1);QuickSort(num, mid + 1, right);}
}
算法分析
时间复杂度:O ( n ∗ l o g n )
空间复杂度:O ( l o g n )
稳定性:不稳定排序
堆排序(Heap Sort)
堆的定义
本文的堆是指数据结构堆,不是内存模型的堆。堆是树型结构,满足 ① 堆是一棵完全树 ② 堆中任意节点值总不大于(不小于)其子节点值 ; 大顶堆的堆顶是最大值,小顶堆则是最小值 ,常见堆有二叉堆、左倾堆、斜堆、二项堆、斐波那契堆等
二叉堆定义
堆通过 数组 实现,父节点和子节点位置存在一定关系
有时将二叉堆第一个元素放在数组索引 0 位置,有时放在 1 位置
若第一个元素放在数组索引 0 位置,则父节点和子节点关系如下:
1、索引为 i 的左孩子的索引是 (2 * i + 1)
2、索引为 i 的左孩子的索引是 (2 * i + 2)
3、索引为 i 的父结点的索引是 floor(( i - 1) / 2) 向下取整
![[[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-csIiN8dX-1676381476585)(E:\2022年MD文档\2023 年 MD文档\二月\浅谈系列\面试浅谈之十大排序算法.assets\182342224903953.jpg)]]](https://img-blog.csdnimg.cn/ce50292363f14c8980efdea8ef771611.png)
若第一个元素放在数组索引 1 位置,则父节点和子节点关系如下:
1、索引为 i 左孩子的索引是
2*i2、索引为 i 右孩子的索引是
2 * i + 13、索引为 i 父结点的索引是
floor( i / 2)
![[[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NJUgULJO-1676381476585)(E:\2022年MD文档\2023 年 MD文档\二月\浅谈系列\面试浅谈之十大排序算法.assets\182343402241540.jpg)]]](https://img-blog.csdnimg.cn/cac26fd9230040bf8ddfb8501769312b.png)
二叉堆的图文解析
二叉堆核心是 添加 和 删除,以 最大堆 举例
添加
在最大堆 [90, 80, 70, 60, 40, 30, 20, 10, 50] 种添加 85,步骤如下
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-075Yte6K-1676381476586)(E:\2022年MD文档\2023 年 MD文档\二月\浅谈系列\面试浅谈之十大排序算法.assets\182345301461858.jpg)]](https://img-blog.csdnimg.cn/11f51e17181d4e7dad4ad1ca98d14489.png)
向最大堆添加数据时 :先将数据加到最大堆末尾,然后尽可能把这个元素往上挪,直至挪不动
删除
在最大堆 [90, 85, 70, 60, 80, 30, 20, 10, 50, 40] 中删除 90,步骤如下
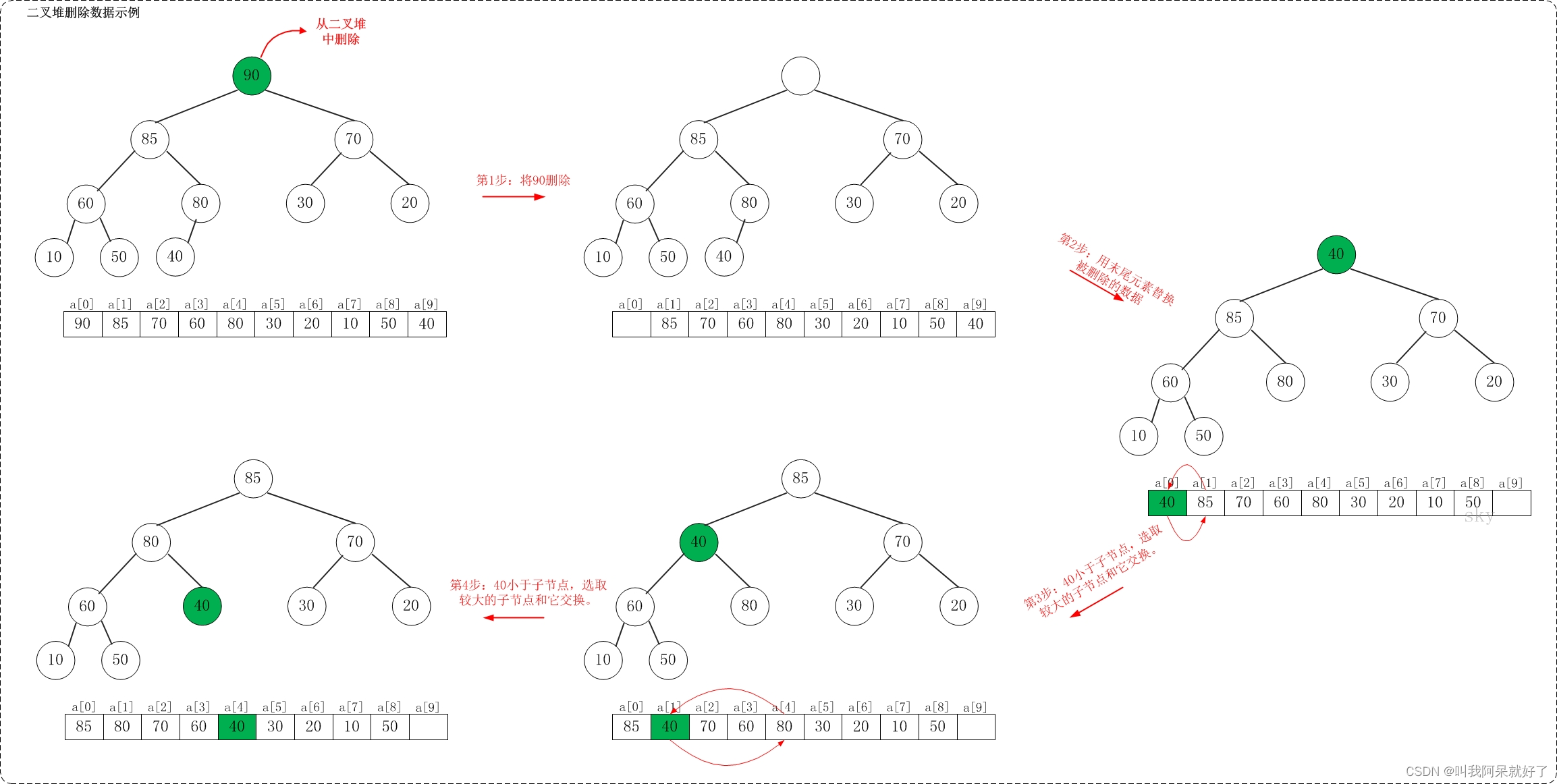
从最大堆中删除数据,先删除该数据,然后用最大堆中最后一个元素插入这个空位;接着,把这个 空位 尽量往上挪,直到剩余数据变成一个最大堆(替换后树仍要是最大堆)
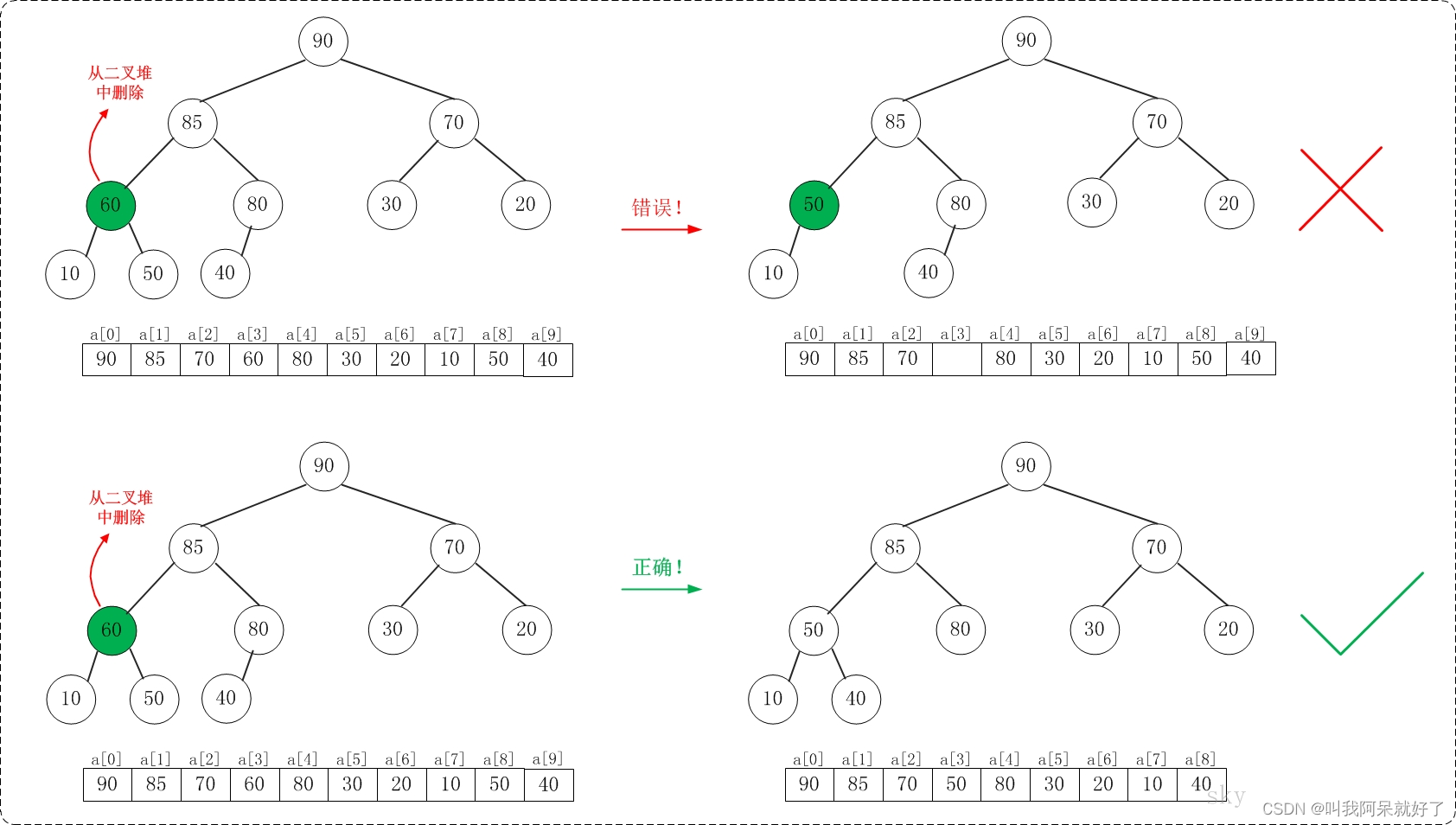
堆排,把堆顶元素与最后一个元素交换,交换后破坏堆特性,把堆中元素再次构成大顶堆,然后把堆顶元素与最后第二个元素交换,循环至剩余元素只有一个
// 下沉操作
void downAdjust(vector<int> &num, int parent, int n) { // 临时保存要下沉的元素 int temp = num[parent]; // 定位左孩子节点的位置int child = 2 * parent + 1; // 开始下沉while (child <= n) {// 如果右孩子节点比左孩子大,则定位到右孩子if (child + 1 <= n && num[child] < num[child + 1])++child;// 如果孩子节点小于或等于父节点,则下沉结束if (num[child] <= temp) break;// 父节点进行下沉num[parent] = num[child];parent = child;child = 2 * parent + 1;}num[parent] = temp; //更新当前下沉值
}void HeapSort(vector<int> &num) {int len = num.size();// 构建大顶堆for (int i = (len - 2) / 2; i >= 0; --i) {downAdjust(num, i, len - 1);}// 进行堆排序for (int i = len - 1; i >= 1; --i) {// 把堆顶元素与最后一个元素交换mySwap(num[0], num[i]);// 把打乱的堆进行调整,恢复堆的特性downAdjust(num, 0, i - 1);}
}
算法分析
时间复杂度:O ( n ∗ l o g n )
空间复杂度:O ( 1 )
稳定性:不稳定排序
计数排序(Counting Sort)
适合最大值和最小值差值不是很大的情况。把数组元素作为数组的下标,然后用一个临时数组统计该元素出现的次数,例如 temp[i] = m, 表示元素 i 一共出现了 m 次。最后再把临时数组统计的数据从小到大汇总起来,此时汇总起来是数据是有序的
代码实现
// 计数排序
void CountingSort(vector<int> &num) { int len = num.size();// 得到数列的最大和最小值int max = num[0], min = num[0]; for (int i = 1; i < len; ++i) { if(num[i] > max) max = num[i]; if (num[i] < min)min = num[i];}// 根据数列最大值确定统计数组的长度vector<int> countArray(max - min + 1, 0);// 遍历数列,填充统计数组for (int i = 0; i < len; ++i) {countArray[num[i] - min]++;}// 遍历统计数组,输出结果 int index = 0; for (int i = 0; i < countArray.size(); ++i) {for (int j = 0; j < countArray[i]; ++j) {num[index++] = i + min;}}
}
算法分析
时间复杂度:O ( n + k ) ,其中 k 为临时数组大小
空间复杂度:O ( k )
稳定性:稳定排序
桶排序(Bucket Sort)
把最大值和最小值之间数进行瓜分,例如分成 10 个区间,10个区间对应10个桶,把各元素放到对应区间桶中,再对每个桶中的数进行排序,可以采用归并排序、快速排序等方法。之后每个桶里面的数据就是有序的了,按顺序遍历各桶即可得到排序序列(桶排序也可用于浮点数排序)
动图演示
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2kGVW6pt-1676381476587)(https://cdn-1301239564.cos.ap-beijing.myqcloud.com/image/programming/%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95/%E6%A1%B6%E6%8E%92%E5%BA%8F%E6%AD%A5%E9%AA%A4.png)]](https://img-blog.csdnimg.cn/77179cb949a141d3ae246acd501a5464.png)
代码实现
// 桶排序
// 有负数的话需要进行预处理, 本函数包含预处理部分
void BucketSort(vector<int> &num) { int len = num.size();// 得到数列的最大最小值int max = num[0], min = num[0]; for(int i = 1; i < len; ++i) { if(num[i] > max) max = num[i]; if (num[i] < min)min = num[i];}// 计算桶的数量并初始化int bucketNum = (max - min) / len + 1;vector<int> vec;vector<vector<int>> bucket;for (int i = 0; i < bucketNum; ++i)bucket.push_back(vec);// 将每个元素放入桶for (int i = 0; i < len; ++i) {// 减去最小值,处理后均为非负数int pos = (num[i] - min) / len;bucket[pos].push_back(num[i]);}// 对每个桶进行排序,此处可选择不同排序方法for (int i = 0; i < bucket.size(); ++i) sort(bucket[i].begin(), bucket[i].end());// 将桶中的元素赋值到原序列int index = 0;for (int i = 0; i < bucketNum; ++i)for(int j = 0; j < bucket[i].size(); ++j)num[index++] = bucket[i][j];
}
算法分析
时间复杂度:O ( n + k )
空间复杂度:O ( k )
稳定性:稳定排序
基数排序(Radix Sort)
先以个位数的大小来对数据进行排序,接着以十位数的大小来进行排序,接着以百位数的大小 ……
以某位数进行排序时,用 桶 来排序,由于某位数(个位/十位….,不是一整个数)的大小范围为0~9,所以我们需要10个桶,然后把具有相同数值数放进同一个桶里,之后再把桶里的数按照 0 号桶到 9 号桶的顺序取出来。一趟下来按照某位数的排序就完成了
代码实现
// 基数排序
// 有负数的话需要进行预处理,本函数不包含预处理部分
void RadixSort(vector<int> &num) {int len = num.size();// 得到数列的最大值int max = num[0]; for (int i = 1; i < len; ++i) { if(num[i] > max) max = num[i];}// 计算最大值是几位数int times = 1;while (max / 10 > 0) {++times;max /= 10;}// 创建10个桶vector<int> vec;vector<vector<int>> bucket;for (int i = 0; i < 10; ++i) {bucket.push_back(vec);}// 进行每一趟的排序,从个位数开始排for (int i = 1; i <= times; i++) {for (int j = 0; j < len; j++) {// 获取每个数最后第 i 位对应桶的位置int radio = (num[j] / (int)pow(10,i-1)) % 10;// 放进对应的桶里bucket[radio].push_back(num[j]);}// 合并放回原数组int k = 0;for (int j = 0; j < 10; j++) {for (int& t : bucket[j]) {num[k++] = t;}//合并之后清空桶bucket[j].clear();} }
}
算法分析
时间复杂度:O ( k ∗ n )
空间复杂度:O ( k + n )
稳定性:稳定排序
三 🏠 结语
身处于这个浮躁的社会,却有耐心看到这里,你一定是个很厉害的人吧 👍👍👍
各位博友觉得文章有帮助的话,别忘了点赞 + 关注哦,你们的鼓励就是我最大的动力
博主还会不断更新更优质的内容,加油吧!技术人! 💪💪💪
相关文章:

面试浅谈之十大排序算法
面试浅谈之十大排序算法 HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是面试浅谈系列,收录在专栏面试中 😜😜😜 本系列将记录一些阿呆个人整理的面试题 🏃&…...

LeetCode-1250. 检查「好数组」【数论,裴蜀定理】
LeetCode-1250. 检查「好数组」【数论,裴蜀定理】题目描述:解题思路一:裴蜀定理是:a*xb*y1。其中a,b是数组中的数,x,y是任意整数。如果a,b互质那么一定有解。问题即转换为寻找互质的数。解题思路二:简化代码…...

【Linux】NTP时间同步服务与NFS网络文件共享存储服务器(配置、测试)
一、NTP时间同步服务1、NTP介绍NTP服务器【Network Time Protocol(NTP)】是用来使计算机时间同步化的一种协议,它可以使计机对其服务器或时钟源(如石英钟,GPS等等)做同步化,它可以提供高精准度的时间校正&a…...
windows下php连接oracle安装oci8扩展报错(PHP Startup: Unable to load dynamic library ‘oci8_11g‘)
记录一下php7.29安装oci8的艰苦过程,简直就是唐僧西天取经历经九九八十一难。 使用的是phpstudy_pro安装的ph扩展wnmp环境下; 1 、安装oralce Instant Client 首先,安装oci8和pdo_oci扩展依赖的Oracle client。了解到需要连接的Oracle版…...

TensorRT的功能
TensorRT的功能 文章目录TensorRT的功能2.1. C and Python APIs2.2. The Programming Model2.2.2. The Runtime Phase2.3. Plugins2.4. Types and Precision2.5. Quantization2.6. Tensors and Data Formats2.7. Dynamic Shapes2.8. DLA2.9. Updating Weights2.10. trtexec本章…...
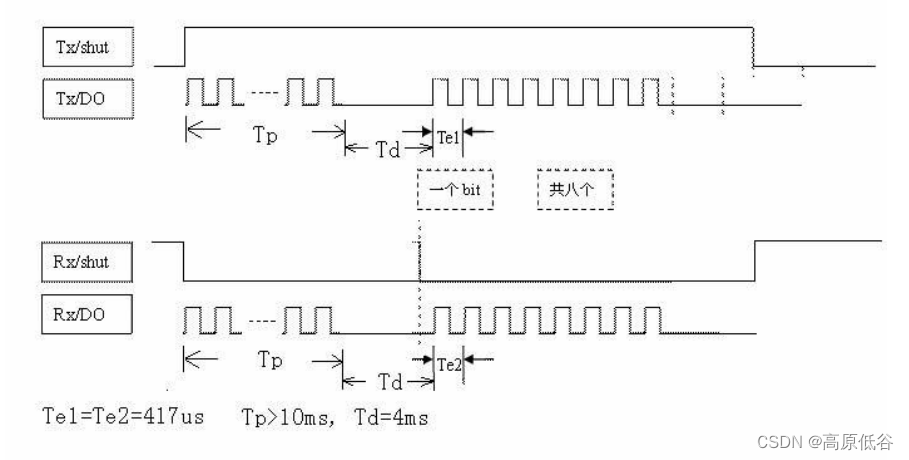
433MHz无线通信--模块RXB90
1、接收模块RXB90简介 两个数据输出是联通的。 2、自定义一个编码解码规则 组数据为“0x88 0x03 0xBD 0xB6”。 3、发射模块 如何使用示波器得到捕捉一个周期的图像? 通过date引脚连接示波器CH1,以及示波器探针的接地端接芯片的GND,分…...
-2PC核心源码解读)
Seata源码学习(三)-2PC核心源码解读
Seata源码分析-2PC核心源码解读 2PC提交源码流程 上节课我们分析到了GlobalTransactionalInterceptor全局事务拦截器,一旦执行拦截器,我们就会进入到其中的invoke方法,在这其中会做一些GlobalTransactional注解的判断,如果有注解…...

IO流概述
🏡个人主页 : 守夜人st 🚀系列专栏:Java …持续更新中敬请关注… 🙉博主简介:软件工程专业,在校学生,写博客是为了总结回顾一些所学知识点 目录IO流概述IO 流的分类总结流的四大类字…...

【node.js】node.js的安装和配置
文章目录前言下载和安装Path环境变量测试推荐插件总结前言 Node.js是一个在服务器端可以解析和执行JavaScript代码的运行环境,也可以说是一个运行时平台,仍然使用JavaScript作为开发语言,但是提供了一些功能性的API。 下载和安装 Node.js的官…...

Python优化算法—遗传算法
Python优化算法—遗传算法一、前言二、安装三、遗传算法3.1 自定义函数3.2 遗传算法进行整数规划3.3 遗传算法用于旅行商问题3.4 使用遗传算法进行曲线拟合一、前言 优化算法,尤其是启发式的仿生智能算法在最近很火,它适用于解决管理学,运筹…...
的应用价值剖析)
数据埋点(Data buried point)的应用价值剖析
一、什么是数据埋点?数据埋点指在应用中特定的流程中收集一些信息,用来跟踪应用使用的状况,后续用来进一步优化产品或是提供运营的数据支撑。比如访问数(Visits),访客数(Visitor),停…...

一文弄懂硬链接、软链接、复制的区别
复制 命令:cp file1 file2 作用:实现对file1的一个拷贝。 限制:可以跨分区,文件夹有效。 效果:修改file1,对file2无影响;修改file2,对file1无影响。删除file1,对file…...
界面组件Telerik ThemeBuilder R1 2023开创应用主题研发新方式!
Telerik DevCraft包含一个完整的产品栈来构建您下一个Web、移动和桌面应用程序。它使用HTML和每个.NET平台的UI库,加快开发速度。Telerik DevCraft提供最完整的工具箱,用于构建现代和面向未来的业务应用程序,目前提供UI for ASP.NET包含一个完…...

在FederatedScope 如何查看clientserver之间的传递的参数大小(通讯量)? 对源码的探索记录
在FederatedScope 如何查看client/server之间的传递的参数大小(通讯量)? 对源码的探索记录 背景需求 想给自己的论文补一个通讯开销对比实验:需要计算出client和server之间传递的信息(例如,模型权重、embedding)总共…...

2023爱分析 · 数据科学与机器学习平台厂商全景报告 | 爱分析报告
报告编委 黄勇 爱分析合伙人&首席分析师 孟晨静 爱分析分析师 目录 1. 研究范围定义 2. 厂商全景地图 3. 市场分析与厂商评估 4. 入选厂商列表 1. 研究范围定义 研究范围 经济新常态下,如何对海量数据进行分析挖掘以支撑敏捷决策、适应市场的快…...

20230215_数据库过程_高质量发展
高质量发展 —一、运营结果 SQL_STRING:‘delete shzc.np_rec_lnpdb a where exists (select * from tbcs.v_np_rec_lnpdbbcv t where a.telnumt.telnum and a.outcarriert.OUTCARRIER and a.incarriert.INCARRIER and a.owncarriert.OWNCARRIER and a.starttimet.STARTTIME …...

【百度 JavaScript API v3.0】LocalSearch 位置检索、Autocomplete 结果提示
地名检索移动到指定坐标 需求 在输入框中搜索,在下拉列表中浮动,右侧出现高亮的列表集。选中之后移动到指定坐标。 技术点 官网地址: JavaScript API - 快速入门 | 百度地图API SDK 开发文档:百度地图JSAPI 3.0类参考 实现 …...

运用Facebook投放,如何制定有效的竞价策略?
广告投放中,我们经常会遇到一个问题,就是不知道什么样的广告适合自己的业务。其实,最简单的方法就是根据我们业务本身进行定位并进行投放。当你了解了广告主所处行业及目标受众后,接下来会针对目标市场进行搜索和定位(…...

大数据框架之Hadoop:HDFS(五)NameNode和SecondaryNameNode(面试开发重点)
5.1NN和2NN工作机制 5.1.1思考:NameNode中的元数据是存储在哪里的? 首先,我们做个假设,如果存储在NameNode节点的磁盘中,因为经常需要进行随机访问,还有响应客户请求,必然是效率过低。因此&am…...

计算机网络 - 1. 体系结构
目录概念、功能、组成、分类概念功能组成分类分层结构概念总结OSI 七层模型应用层表示层会话层传输层网络层数据链路层物理层TCP/IP 四层模型OSI 与 TCP/IP 相同点OSI 与 TCP/IP 不同点为什么 TCP/IP 去除了表示层和会话层五层参考模型概念、功能、组成、分类 概念 …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
