05- 线性回归算法 (LinearRegression) (算法)
- 线性回归算法(LinearRegression)就是假定一个数据集合预测值与实际值存在一定的误差, 然后假定所有的这些误差值符合正太分布, 通过方程求这个正太分布的最小均值和方差来还原原数据集合的斜率和截距。
- 当误差值无限接近于0时, 预测值与实际值一致, 就变成了求误差的极小值。
from sklearn.linear_model import LinearRegression
model = LinearRegression() # 使用模型
model.fit(X,y)w_ = model.coef_ # 斜率
b_ = model.intercept_ # 截距θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # [[3.97] [7.19]] 矩阵求解1、基本概念
线性回归是机器学习中有监督机器学习下的一种算法。 回归问题主要关注的是因变量(需要预测的值,可以是一个也可以是多个)和一个或多个数值型的自变量(预测变量)之间的关系。
- 需要预测的值:即目标变量,target,y,连续值预测变量。
- 影响目标变量的因素:
,可以是连续值也可以是离散值。
- 因变量和自变量之间的关系:即模型,model,是我们要求解的。
1.1、连续值和离散值
比如人的身高和全国的省份分布
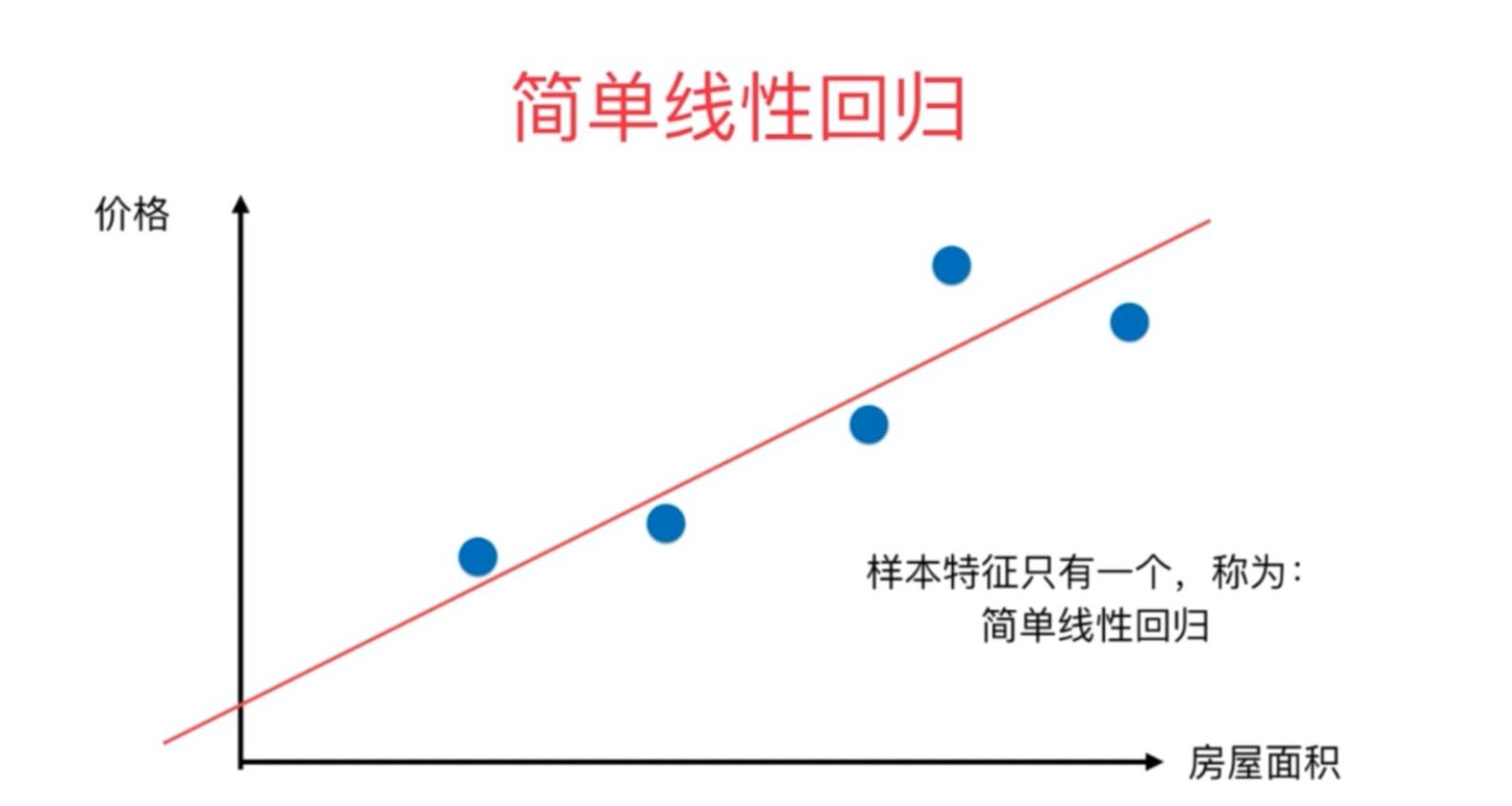
1.2、简单线性回归
简单线性回归属于一个算法,它所对应的公式。
1.3、最优解
最优解:尽可能的找到一个模型使得整体的误差最小,整体的误差通常叫做损失 Loss。
- Actual value: 真实值,一般使用 y 表示,实际值。
- Predicted value: 预测值,是把已知的 x 带入到公式里面和猜出来的参数 w,b 计算得到的,一般使用y_表示。
- error: 误差,预测值和真实值的差距,一般使用 ϵ 表示。
- 最优解: 尽可能的找到一个模型使得整体的误差最小,整体的误差通常叫做损失 Loss。
- Loss: 整体的误差,Loss 通过损失函数 Loss function 计算得到。
1.4、多元线性回归
现实生活中,往往影响结果 y 的因素不止一个,这时 x 就从一个变成了 n 个,X1,X2…Xn同时简单线性回归的公式也就不在适用了。多元线性回归公式如下:
b是截距,也可以使用来表示
使用向量来表示, 表示所有的变量,是一维向量;
表示所有的系数(包含
),是一维向量,根据向量乘法规律:

2、正规方程
2.1、最小二乘法矩阵表示
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下:
或者
,其中的
和
即使方程的解!
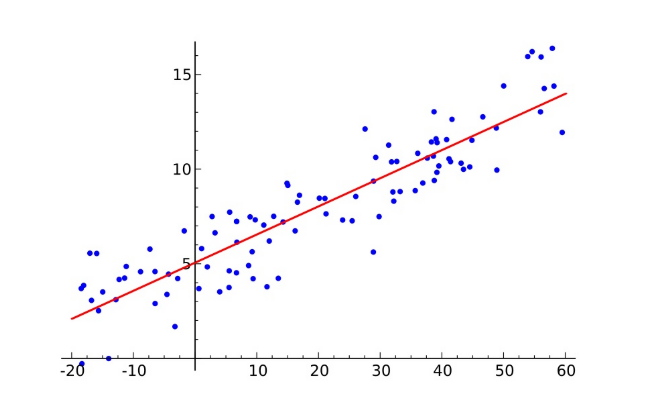
最小二乘法公式:
使用矩阵表示:

2.2、多元一次方程举例
三元一次方程 :
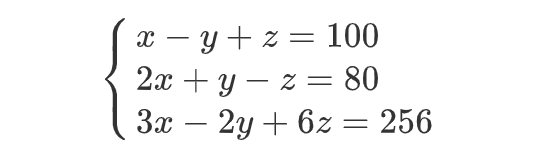
通过矩阵可以直接求解: # 通过逆矩阵进行求解
# 上面八元一次方程对应的X数据
X = np.array( [[1, -1, 1], [2, 1, -1], [2, -2, 6]])
# 对应的y
y = np.array([100, 80, 256])
np.linalg.solve(X,y).round(2) # array([ 60., -26., 14.])2.3、推导正规方程  的解
的解
- 矩阵乘法公式展开
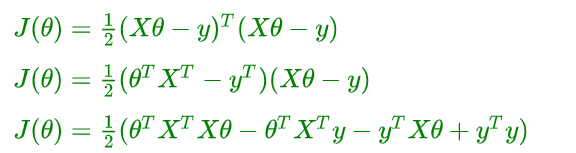
- 使用逆矩阵进行转化

2.4、凸函数判定
判定损失函数是凸函数的好处在于我们可能很肯定的知道我们求得的极值即最优解,一定是全局最优解。

判定凸函数的方式: 判定凸函数的方式非常多,其中一个方法是看黑塞矩阵是否是半正定的。
- 黑塞矩阵(hessian matrix)是由目标函数在点 X 处的二阶偏导数组成的对称矩阵。在导函数的基础上再次对θ来求偏导,结果全为正时为正定,如果结果大于等于0, 就是半正定。判定极小值.

- 在机器学习中往往损失函数都是凸函数,到深度学习中损失函数往往是非凸函数,即找到的解未必是全局最优,只要模型堪用就好!机器学习特点是:不强调模型 100% 正确,只要是有价值的,堪用的,就Okay!
3、线性回归算法推导
人类社会很多事情都被大自然这种神奇的力量只配置:身高、体重、智商、相貌……这种神秘的力量就叫正态分布。大数学家高斯,深入研究了正态分布,最终推导出了线性回归的原理:最小二乘法!
3.1、误差分析
误差等于第 i 个样本实际的值减去预测的值,公式可以表达为如下:
或
假定所有的样本的误差都是独立的,有上下的震荡,震荡认为是随机变量,足够多的随机变量叠加之后形成的分布,它服从的就是正态分布,因为它是正常状态下的分布,也就是高斯分布!均值是某一个值,方差是某一个值。 方差我们先不管,均值我们总有办法让它去等于零 0 的,因为我们这里是有截距b, 所有误差我们就可以认为是独立分布的,1<=i<=n,服从均值为 0,方差为某定值的高斯分布。机器学习中我们假设误差符合均值为0,方差为定值的正态分布.将误差定义到正太分布中.当样本足够多的时候,取样本的均值则为实际值.
3.2、最大似然估计
最大似然估计(maximum likelihood estimation, MLE)一种重要而普遍的求估计量的方法。最大似然估计明确地使用概率模型,其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然估计是一类完全基于统计的系统发生树重建方法的代表。
3.3、高斯分布-概率密度函数
最常见的连续概率分布是正态分布,也叫高斯分布,而这正是我们所需要的,其概率密度函数如下:

正态分布 公式如下:

随着参数μ和σ变化,概率分布也产生变化。 下面重要的步骤来了,我们要把一组数据误差出现的总似然,也就是一组数据之所以对应误差出现的整体可能性表达出来了,因为数据的误差我们假设服从一个高斯分布,并且通过截距项来平移整体分布的位置从而使得μ=0.
3.4、误差总似然, 最小二乘法MSE
这种最小二乘法估计,其实我们就可以认为,假定了误差服从正太分布,认为样本误差的出现是随机的,独立的,使用最大似然估计思想,利用损失函数最小化 MSE 就能求出最优解!所以反过来说,如果我们的数据误差不是互相独立的,或者不是随机出现的,那么就不适合去假设为正太分布,就不能去用正太分布的概率密度函数带入到总似然的函数中,故而就不能用 MSE 作为损失函数去求解最优解了!
还有譬如假设误差服从泊松分布,或其他分布那就得用其他分布的概率密度函数去推导出损失函数了。
所以有时我们也可以把线性回归看成是广义线性回归。比如,逻辑回归,泊松回归都属于广义线性回归的一种,这里我们线性回归可以说是最小二乘线性回归。
4、线性回归实战
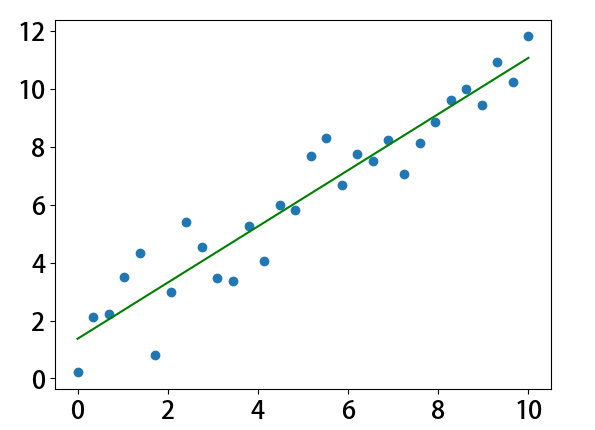
4.1、简单线性回归
一元一次方程,在机器学习中一元表示一个特征,b表示截距,y表示目标值。
import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 重新构造X,b截距,相当于系数w0,前面统一乘以1
X = np.concatenate([X,np.full(shape = (30,1),fill_value= 1)],axis = 1)
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # 根据公式计算
print('一元一次方程真实的斜率和截距是:',w, b)
print('通过正规方程求解的斜率和截距是:',θ)
# 根据求解的斜率和截距绘制线性回归线型图
plt.plot(X[:,0],X.dot(θ),color = 'green')
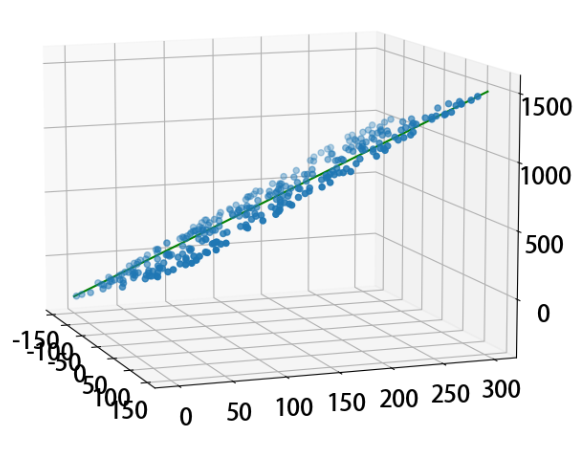
4.2、多元线性回归
二元一次方程,x1, x2相当于两个特征,b是方程截距
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X,将x1、x2以及截距b,相当于系数w0,前面统一乘以1进行数据合并
X = np.concatenate([x1,x2,np.full(shape = (300,1),fill_value=1)],axis = 1)
w = np.concatenate([w,b])
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # 计算公式
print('二元一次方程真实的斜率和截距是:',w)
print('通过正规方程求解的斜率和截距是:',θ.reshape(-1))
# # 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * θ[0] + y * θ[1] + θ[2]
ax.plot(x,y,z ,color = 'red')

4.3、机器学习库scikit-learn
一元线性回归:
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 使用scikit-learn中的线性回归求解
model = LinearRegression() # 使用模型
model.fit(X,y)
w_ = model.coef_
b_ = model.intercept_
print('一元一次方程真实的斜率和截距是:',w, b)
print('通过scikit-learn求解的斜率和截距是:',w_,b_)
plt.plot(X,X.dot(w_) + b_,color = 'green')

多元线性回归:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
from sklearn.linear_model import LinearRegression
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X,将x1、x2以及截距b,相当于系数w0,前面统一乘以1进行数据合并
X = np.concatenate([x1,x2],axis = 1)
# 使用scikit-learn中的线性回归求解
model = LinearRegression() # 使用模型
model.fit(X,y)
w_ = model.coef_.reshape(-1)
b_ = model.intercept_
print('二元一次方程真实的斜率和截距是:',w,b) # [2, 4] [1]
print('通过scikit-learn求解的斜率和截距是:',w_,b_) # [1.99997 3.99976] [0.88129]
# 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * w_[0] + y * w_[1] + b_
ax.plot(x,y,z ,color = 'green')
相关文章:

05- 线性回归算法 (LinearRegression) (算法)
线性回归算法(LinearRegression)就是假定一个数据集合预测值与实际值存在一定的误差, 然后假定所有的这些误差值符合正太分布, 通过方程求这个正太分布的最小均值和方差来还原原数据集合的斜率和截距。当误差值无限接近于0时, 预测值与实际值一致, 就变成了求误差的极小值。 fr…...

JAVA补充知识01之枚举enum
目录 1. 枚举类的使用 1.1 枚举类的理解 1.2 举例 1.3 开发中的建议: 1.4 Enum中的常用方法 1.5 熟悉Enum类中常用的方法 1.6 枚举类实现接口的操作 1.7 jdk5.0之前定义枚举类的方式 (了解即可) 1.8 jdk5.0之后定义枚举类的方式 1…...
jenkins下配置maven
1. 先在jenkins服务器上安装maven 下载-解压-重命名-启动 [rootVM-0-12-centos local]# wget https://mirrors.aliyun.com/apache/maven/maven-3/3.9.0/binaries/apache-maven-3.9.0-bin.tar.gz [rootVM-0-12-centos local]# tar xf apache-maven-3.9.0-bin.tar.gz [rootVM-0…...

春季开学即将到来!大学生活必备数码清单奉上
马上就要开学了,你的返校装备是否已经准备齐全了呢?对于高校学生来说,很多数码产品都属于必备装备,比如下面这几款产品就受到了大量年轻消费者的喜爱,在它们的帮助下能够让大家的学习时光变得更快乐。1、不入耳黑科技骨…...
ubuntu18.04 天选2 R95900hx 3060显卡驱动安装
天选2 R95900hx 3060显卡驱动安装需求问题解决内核集显显卡驱动需求 外接显示器,安装nvidia驱动 问题 由于一开始直接在软件和更新中附加读懂安装了nvidia-470,导致系统黑屏。 解决 grub页面系统选择进入ubuntu recovery模式,选择root&a…...
Harbor安装部署实战详细手册
文章目录前言一、安装docker二、安装docker-compose1.下载2.赋权3.测试三、安装harbor1.下载2.解压3.修改配置文件4.部署5.配置开机自启动6.登录验证7.补充说明四、harbor使用问题1.docker login问题:Error response from daemon: Get https://: http: server gave …...
)
华为OD机试真题JAVA实现【箱子之形摆放】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述示例一输入输出说明备注解题思路Code运行结果版权说明...
| 真题+思路+考点+代码+岗位)
华为OD机试 - 事件推送(Python)| 真题+思路+考点+代码+岗位
事件推送 题目 同一个数轴 X 上有两个点的集合 A={A1, A2, …, Am} 和 B={B1, B2, …, Bn}, Ai 和 Bj 均为正整数,A、B 已经按照从小到大排好序,A、B 均不为空, 给定一个距离 R (正整数), 列出同时满足如下条件的所有(Ai, Bj)数对: Ai <= BjAi, Bj 之间的距离小于…...

【Linux】信号量
🎇Linux: 博客主页:一起去看日落吗分享博主的在Linux中学习到的知识和遇到的问题博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 看似不起波澜的日复一日,一定会在某一天让你看见坚持…...

android-java同步方法和异步方法
接口 Java接口是一系列方法的声明,是一些方法特征的集合,一个接口只有方法的特征没有方法的实现,因此这些方法可以在不同的地方被不同的类实现,而这些实现可以具有不同的行为(功能)。 两种含义:…...
:请求和响应)
Flask入门(5):请求和响应
目录5.请求和响应5.1 请求5.2 响应5.请求和响应 5.1 请求 request对象封装解析了请求报文中的数据,其大部分功能是由依赖包werkzeug完成的,并且每个request对象都是线程隔离的,保证了数据的安全性。 request对象的属性 1.request.method …...
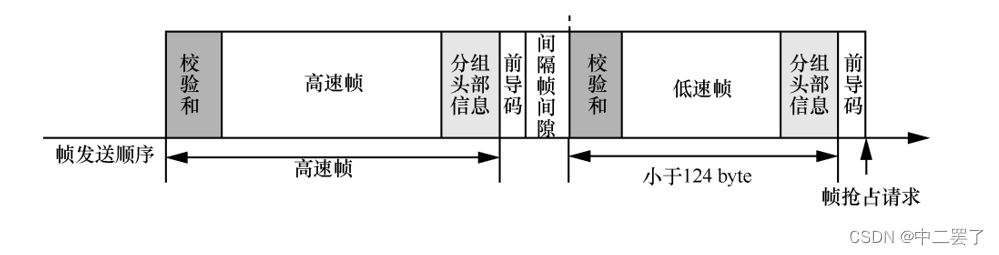
记进组后第五次组会汇报
2023年2月14日 日记一、小组组会二、实验室组会1、汇报内容(1)参考文献(2)CQF机制a.研究现状b.相关思考(3)研究计划2、汇报反馈一、小组组会 上午十点整,小组组会开始,有两个同学我…...
)
nil Foundation的Placeholder证明系统(2)
前序博客: nil Foundation的Placeholder证明系统(1) nil; Foundation团队2022年11月论文《Placeholder证明系统》。[2022年11月29日版本] 8. 优化 8.1 Batched FRI 不同于单独检查每个commitment,可对其进行FRI聚合。如对多项…...
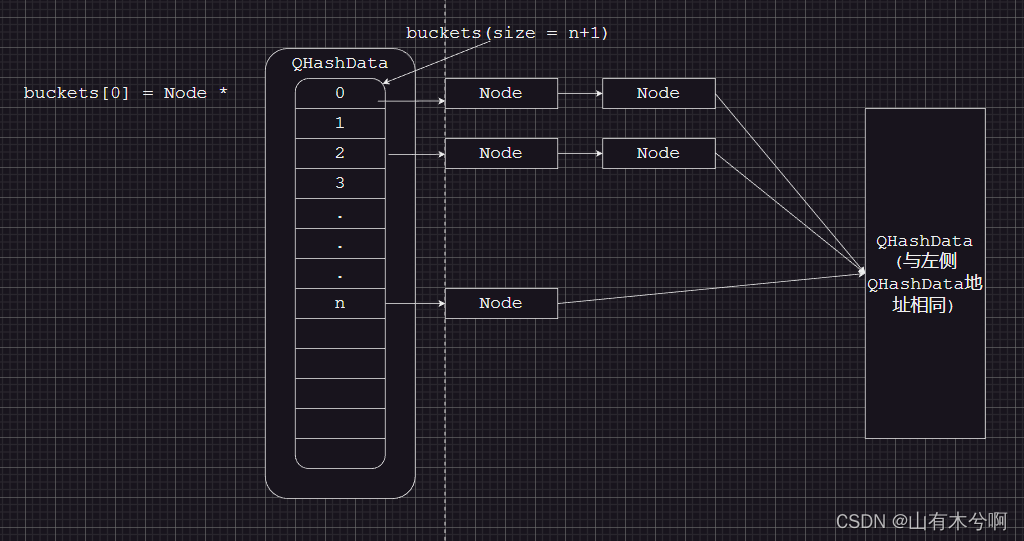
QHash源码解读
QT版本 v5.12.10 元素 // 重点说明QHashData的函数,QHashData是QHash的基础 struct QHashData {struct Node {Node *next;uint h;};Node *fakeNext; // 永为nullNode **buckets; // Node *数组QtPrivate::RefCount ref;int size; // node个数int nodeSize; /…...

【Unity细节】RigidBody中Dynamic和Kinematic的区别
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity细节和bug ⭐Dynamic和Kinematic的区别⭐ 文章目录⭐Dynamic和Kinematic的区别⭐dz…...

【C++、数据结构】哈希 — 闭散列与哈希桶的模拟实现
文章目录📖 前言1. STL中哈希表的两个应用⚡1.1 🌟unordered_set1.2 🌟unordered_map2. 常见查找的性能对比💥3. 哈希表模拟实现🏁3.1 哈希的概念:3.2 哈希函数:3.3 哈希冲突:3.4 闭…...
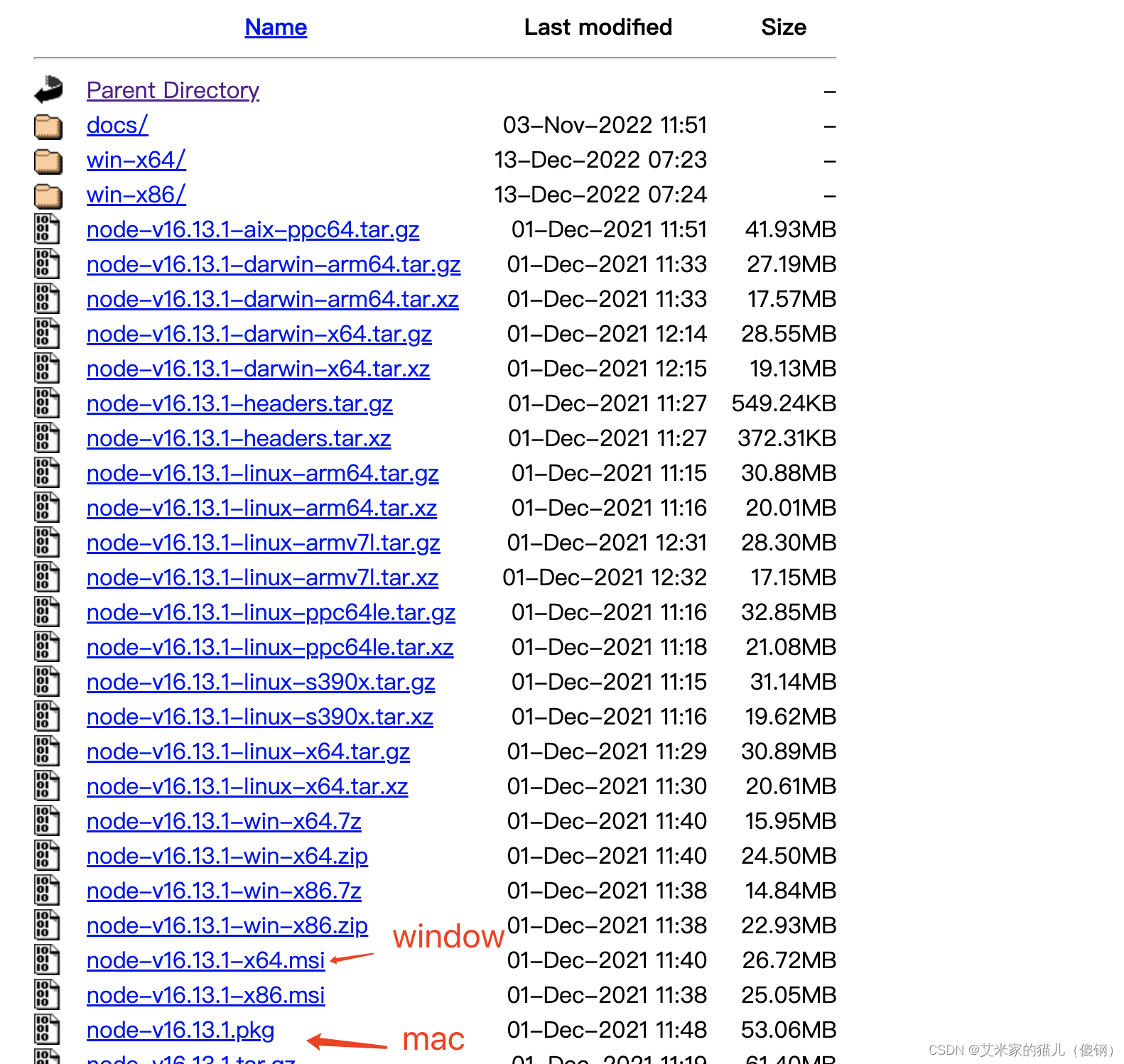
vue 开发环境 卸载node 版本 切换新的 node 版本 mac电脑
注意:操作的机器当前是mac,先卸载,再安装 1.查看现有 node 版本 node -v2.卸载现有 node 版本, 1.卸载从node官网下载pkg安装的node sudo rm -rf /usr/local/{bin/{node,npm},lib/node_modules/npm,lib/node,share/man/*/node…...
在Linux和Windows上安装Nacos-2.1.1
记录:377场景:在CentOS 7.9操作系统安装Nacos-2.1.1。在Windows操作系统上安装Nacos-2.1.1。Nacos:Nacos: Dynamic Naming and Configuration Service。Nacos提供动态配置服务、服务发现及管理、动态DNS服务功能。版本:JDK 1.8 Na…...
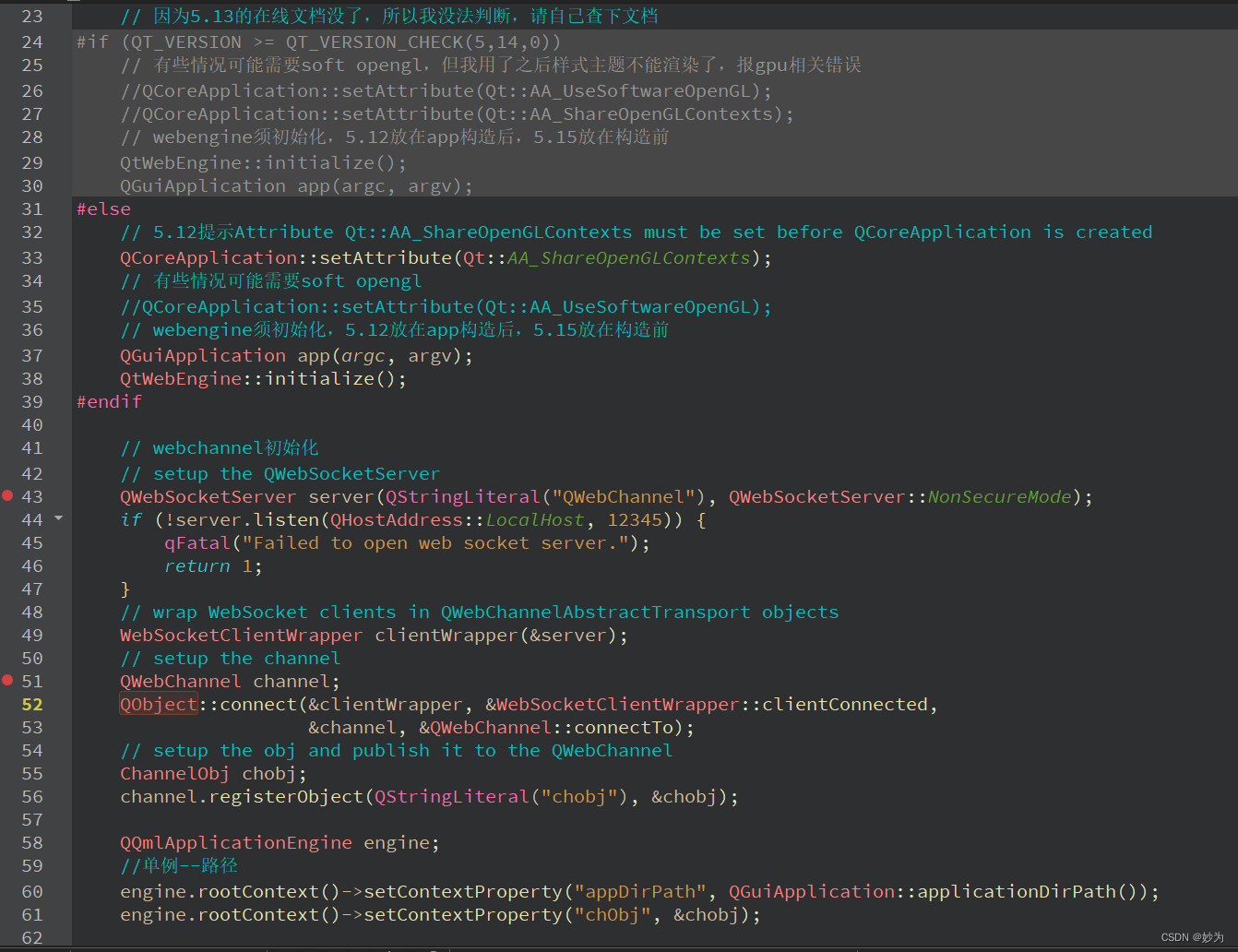
解决QML debugging is enabled.Only use this in a safe environment.警告
系列文章目录 文章目录系列文章目录前言一、警告原因二、解决办法参考前言 我试图运行一个非常简单的程序,当单击退出按钮时关闭窗口,但获取以下输出,前提是包含按钮的应用程序窗口不显示: 您已启用QML调试(实际上它默认启用)&…...
)
华为OD机试真题JAVA实现【N进制减法】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述示例一输入输出说明解题思路Code代码运行结果版权说明<...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
