nil Foundation的Placeholder证明系统(2)
前序博客:
- nil Foundation的Placeholder证明系统(1)
=nil; Foundation团队2022年11月论文《Placeholder证明系统》。[2022年11月29日版本]
8. 优化
8.1 Batched FRI
不同于单独检查每个commitment,可对其进行FRI聚合。如对多项式f0,⋯,fkf_0,\cdots,f_kf0,⋯,fk:
- 1)从transcript中获取θ\thetaθ。
- 2)计算f=f0⋅θk−1+⋯+fkf=f_0\cdot \theta^{k-1}+\cdots+f_kf=f0⋅θk−1+⋯+fk。
- 3)基于fff运行FRI,using oracles to f0,⋯,fkf_0,\cdots,f_kf0,⋯,fk。
从而可对所有committed polynomials只允许依次FRI实例。详细参看RedShift论文。
8.2 Hash By Column
不同于对每个多项式都进行commit,可对多个多项式采用相同的Merkle tree,这样可降低Prover所需提供的Merkle tree paths数量。
详细参看RedShift论文。
8.3 Hash By Subset
每个i+1i+1i+1 FRI round假定Prover发送all elements from a coset H∈D(i)H\in D^{(i)}H∈D(i)。每个Merkle leaf可包含the whole coset instead of separate values。
详细参看RedShift论文。不过RedShift作者在每个leaf中使用了更多的values,从而具有更好的性能。
8.4 FRI PoW
待续。。。。
9. Placeholder参数
本节重点讨论Placeholder参数 及其对协议安全和性能的影响。
9.1 FRI参数
令RS[F,D,ρ]\mathbf{RS}[\mathbb{F},D,\rho]RS[F,D,ρ]为Reed-Solomon code family。此处有∣D∣=n=2k,ρ=2−R(k,RN)|D|=n=2^k,\rho=2^{-R}(k,R\mathbb{N})∣D∣=n=2k,ρ=2−R(k,RN)。这意味着committing polynomials的degree bound为d=2k−Rd=2^{k-R}d=2k−R。
令r∈[1,logd=n^]r\in [1,\log d=\hat{n}]r∈[1,logd=n^]为FRI inner rounds数,lll为repetition参数。
相应的:
- Prover:O(n)\mathcal{O}(n)O(n)
- Verifier:O(logn)\mathcal{O}(\log n)O(logn)
对于每个ϵ∈(0,1]\epsilon\in (0,1]ϵ∈(0,1],令Jϵ:[0,1]→[0,1]J_{\epsilon}:[0,1]\rightarrow [0,1]Jϵ:[0,1]→[0,1]函数为:
Jϵ(X)=1−1−X(1−ϵ)J_{\epsilon}(X)=1-\sqrt{1-X(1-\epsilon)}Jϵ(X)=1−1−X(1−ϵ)
假设Δ(f,RS)=δ>0\Delta(f,\mathbf{RS})=\delta>0Δ(f,RS)=δ>0,则根据Eli Ben-Sasson 2019年论文 DEEP-FRI: Sampling Outside the Box Improves Soundness,相应的soundness error上限为:
err(δ)=2log∣D∣ϵ3∣F∣+(1−min{δ0,Jϵ(1−ρ)}+ϵlog∣D∣)l\mathbf{err}(\delta)=\frac{2\log |D|}{\epsilon^3|\mathbb{F}|}+(1-\min\{\delta_0,J_{\epsilon}(1-\rho)\}+\epsilon \log |D|)^lerr(δ)=ϵ3∣F∣2log∣D∣+(1−min{δ0,Jϵ(1−ρ)}+ϵlog∣D∣)l
9.2 Placeholder参数
当前可将circuit parameters用于FRI commitments。
令ddd为the smallest power of two,使得d≥Nrowsd\geq N_{rows}d≥Nrows。在Placeholder中,ddd定义为the highest degree of polynomials that can be committed by FRI instance。
令www为ddd-th root of unity。有d=2n^d=2^{\hat{n}}d=2n^,且n^≥Nrows\hat{n}\geq N_{rows}n^≥Nrows。
用RS[F,D,ρ]\mathbf{RS}[\mathbb{F},D,\rho]RS[F,D,ρ]来表示FRI commitments,其中:
- F\mathbb{F}F:与PLONK arithmetization中的field相同。
- DDD:为domain of n=2k=2n^+Rn=2^k=2^{\hat{n}+R}n=2k=2n^+R root of unity。
- ρ=2−R\rho=2^{-R}ρ=2−R:为可调整的参数。
Soundness error定义为:
ϵπ(δ)≤max(ϵFRI(δ),ϵIOPN,1F)\epsilon_{\pi}(\delta)\leq\max(\epsilon_{FRI}(\delta),\epsilon_{IOP}^N, \frac{1}{\mathbb{F}})ϵπ(δ)≤max(ϵFRI(δ),ϵIOPN,F1)
其中,ϵIOPN=(Jp,ν)8⋅4nF/D\epsilon_{IOP}^N=(J_{p,\nu })^8\cdot \frac{4n}{\mathbb{F}/D}ϵIOPN=(Jp,ν)8⋅F/D4n
令log∣F∣=255,ν=∣F∣−1/20,D=228\log |\mathbb{F}|=255,\nu=|\mathbb{F}|^{-1/20},D=2^{28}log∣F∣=255,ν=∣F∣−1/20,D=228,其对ϵIOPN\epsilon_{IOP}^NϵIOPN的error contribution量级为2−1282^{-128}2−128。
令ρ=1/16\rho=1/16ρ=1/16,根据上面的FRI error公式,为达到80 bits security ,需要40个verifier queries(λ\lambdaλ)。
【注意,以上参数并未考虑借助”grinding“技术,可进一步降低queries数量。】
10. Circuit性能评估
关键标识有:
| 标识 | 含义 |
|---|---|
| nnn(对应之前NrowsN_{rows}Nrows) | Rows的数量 |
| NwitnessN_{witness}Nwitness | Witness Columns(又名”Advice Columns“)的数量 |
| NpermN_{perm}Nperm | 包含在Permutation Argument中的Witness Columns数量 |
| NselN_{sel}Nsel | Circuit中所使用的Selectors数量 |
| NlookupN_{lookup}Nlookup | |
| NcN_cNc | |
| NPIN_{PI}NPI | |
| wiw_iwi | |
| cj(i)c_j^{(i)}cj(i) | |
| gatei\mathbf{gate}_igatei | Gate Polynomials,0≤i<Nsel0\leq i<N_{sel}0≤i<Nsel。 |
| PIiPI_iPIi | |
| σ(col:i,row:j)=(col:i′,row:j′)\sigma(col:\ i, row:\ j)=(col:\ i', row:\ j')σ(col: i,row: j)=(col: i′,row: j′) | Permutation over the Table |
| o\mathbf{o}o | |
| fi\mathbf{f}_ifi | Witness polynomials,0≤i<Nwitness0\leq i < N_{witness}0≤i<Nwitness |
| fci\mathbf{f}_{c_i}fci | Constant-related polynomials,0≤i<Nconst0\leq i < N_{const}0≤i<Nconst |
| HcH_cHc | Commitment hash |
| HrH_rHr | Random Oracle hash |
| lHcl_{H_c}lHc | Number of bits in commitment hash |
| lHrl_{H_r}lHr | Number of bits in random oracle hash |
10.1 Proof Size
Proof中包含:
- f0,comm,⋯,fNwitness−1,commf_{0,comm},\cdots,f_{N_{witness}-1,comm}f0,comm,⋯,fNwitness−1,comm:对witness多项式的承诺值。
- Acomm′,Scomm′A'_{comm},S'_{comm}Acomm′,Scomm′:为lookup承诺值。
- Pcomm,QcommP_{comm},Q_{comm}Pcomm,Qcomm
- VcommV_{comm}Vcomm:lookup相关
- T0,comm,⋯,TNperm−1,commT_{0,comm},\cdots,T_{N_{perm}-1,comm}T0,comm,⋯,TNperm−1,comm
- Values and paths with size logn\log nlogn:
- fi(y)f_i(y)fi(y) for i∈[0,Nwitness−1]i\in [0, N_{witness}-1]i∈[0,Nwitness−1]
- P(y),P(yw),Q(y),Q(yw)P(y), P(yw),Q(y), Q(yw)P(y),P(yw),Q(y),Q(yw)
- Tj(y)T_j(y)Tj(y) for j∈[0,Nperm−1]j\in [0, N_{perm}-1]j∈[0,Nperm−1]
- A′(y),S′(y),V(y),A′(yw−1),V(yw)A'(y),S'(y), V(y), A'(yw^{-1}),V(yw)A′(y),S′(y),V(y),A′(yw−1),V(yw)
- Gate-depending fi(ywμ)f_i(yw^{\mu})fi(ywμ)
- For circuit polynomials:区分point values
- Evaluation proof for the values above(lll次):
附录 nil Foundation系列博客
- nil Foundation的Solana-Ethereum Bridge Based on Light-Client State Proof Verification
- nil Foundation的基于Solana light client实现的zk-bridge方案
- nil Foundation的Mina->以太坊 bridge原型已完成
- nil Foundation的Mina-Ethereum State Proof Verification Applications
- nil Foundation的in-EVM Full Mina State Verification
- nil Foundation的Placeholder证明系统(1)
- zkLLVM:nil Foundation开发的电路编译器
参考资料
[1] ZCash Halo2 Lookup argument
[2] ZCash Halo2 Permutation argument
相关文章:
)
nil Foundation的Placeholder证明系统(2)
前序博客: nil Foundation的Placeholder证明系统(1) nil; Foundation团队2022年11月论文《Placeholder证明系统》。[2022年11月29日版本] 8. 优化 8.1 Batched FRI 不同于单独检查每个commitment,可对其进行FRI聚合。如对多项…...
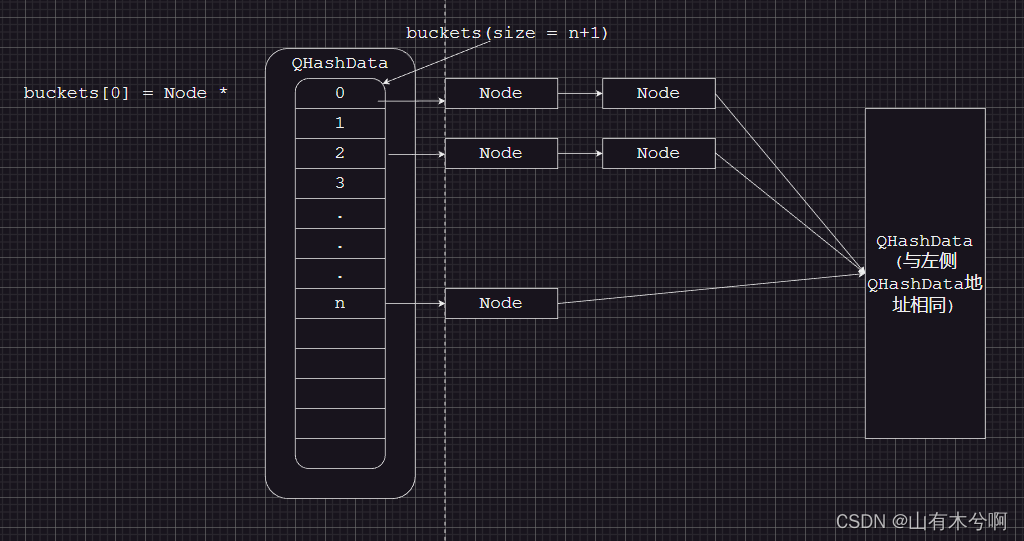
QHash源码解读
QT版本 v5.12.10 元素 // 重点说明QHashData的函数,QHashData是QHash的基础 struct QHashData {struct Node {Node *next;uint h;};Node *fakeNext; // 永为nullNode **buckets; // Node *数组QtPrivate::RefCount ref;int size; // node个数int nodeSize; /…...

【Unity细节】RigidBody中Dynamic和Kinematic的区别
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity细节和bug ⭐Dynamic和Kinematic的区别⭐ 文章目录⭐Dynamic和Kinematic的区别⭐dz…...

【C++、数据结构】哈希 — 闭散列与哈希桶的模拟实现
文章目录📖 前言1. STL中哈希表的两个应用⚡1.1 🌟unordered_set1.2 🌟unordered_map2. 常见查找的性能对比💥3. 哈希表模拟实现🏁3.1 哈希的概念:3.2 哈希函数:3.3 哈希冲突:3.4 闭…...
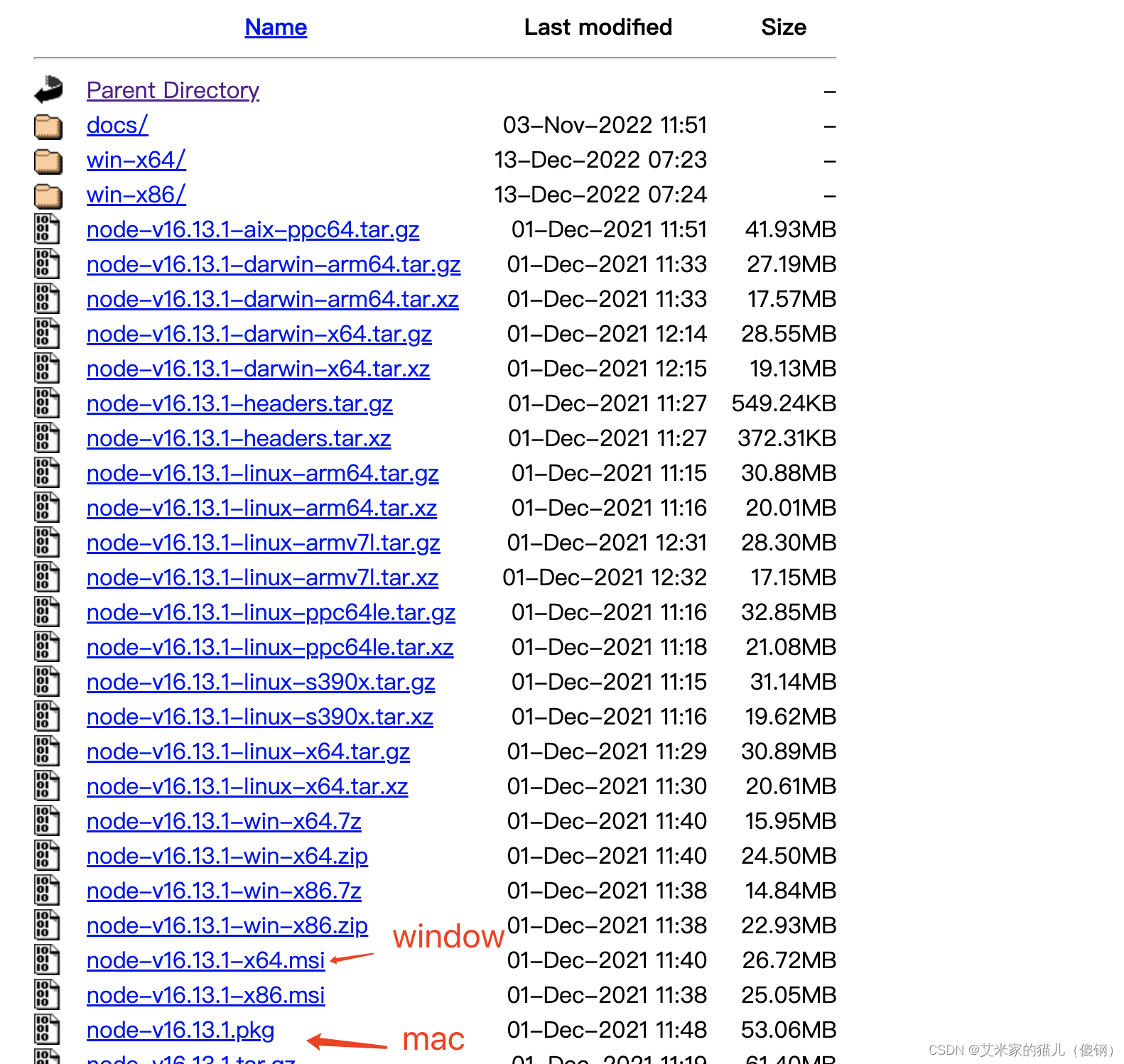
vue 开发环境 卸载node 版本 切换新的 node 版本 mac电脑
注意:操作的机器当前是mac,先卸载,再安装 1.查看现有 node 版本 node -v2.卸载现有 node 版本, 1.卸载从node官网下载pkg安装的node sudo rm -rf /usr/local/{bin/{node,npm},lib/node_modules/npm,lib/node,share/man/*/node…...
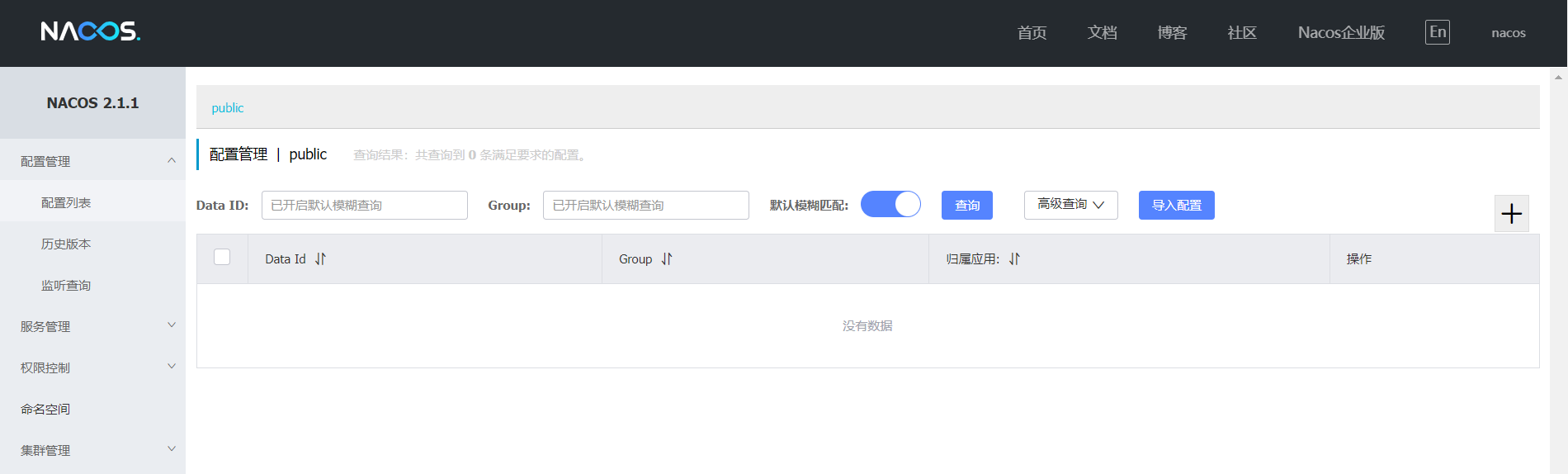
在Linux和Windows上安装Nacos-2.1.1
记录:377场景:在CentOS 7.9操作系统安装Nacos-2.1.1。在Windows操作系统上安装Nacos-2.1.1。Nacos:Nacos: Dynamic Naming and Configuration Service。Nacos提供动态配置服务、服务发现及管理、动态DNS服务功能。版本:JDK 1.8 Na…...
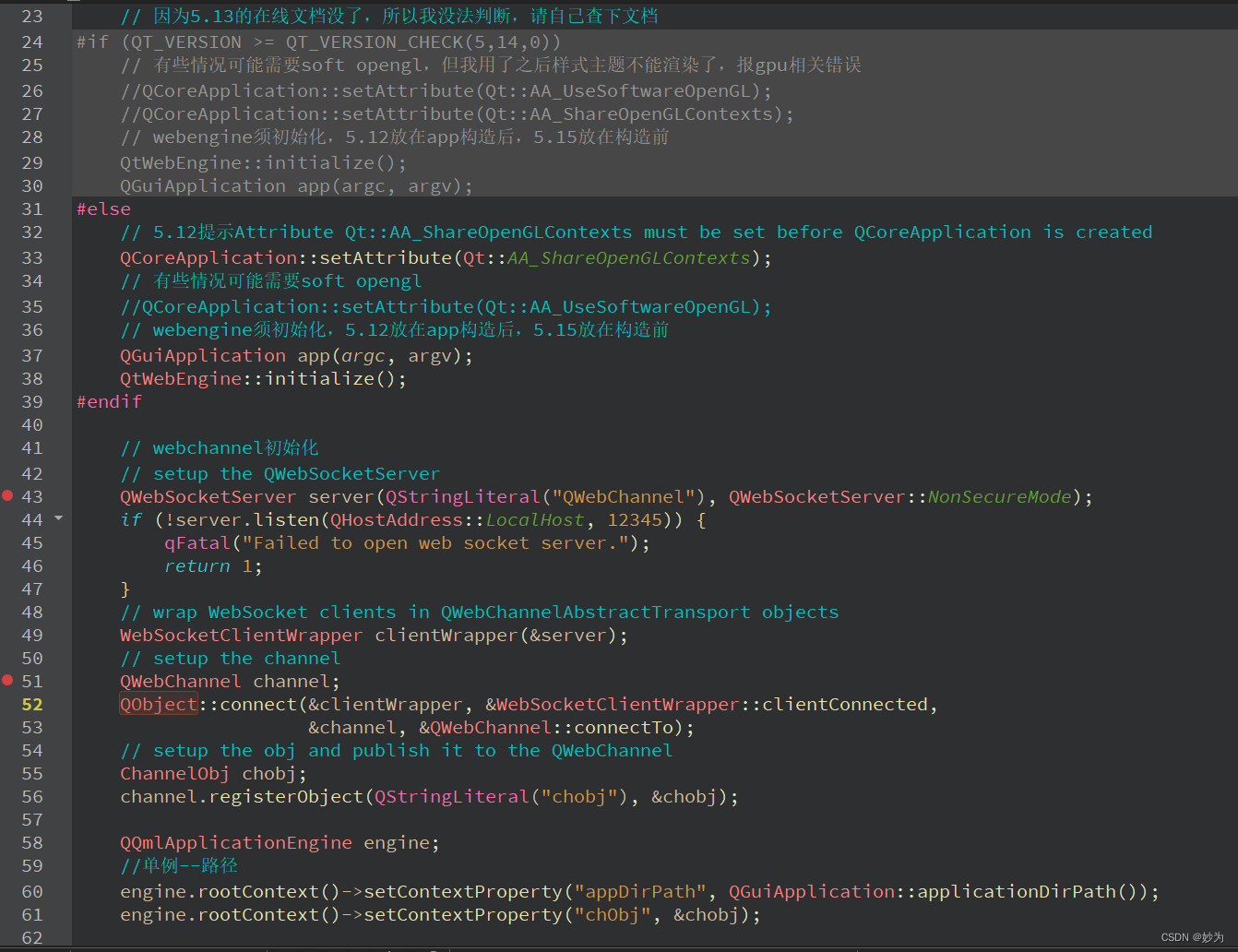
解决QML debugging is enabled.Only use this in a safe environment.警告
系列文章目录 文章目录系列文章目录前言一、警告原因二、解决办法参考前言 我试图运行一个非常简单的程序,当单击退出按钮时关闭窗口,但获取以下输出,前提是包含按钮的应用程序窗口不显示: 您已启用QML调试(实际上它默认启用)&…...
)
华为OD机试真题JAVA实现【N进制减法】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出描述示例一输入输出说明解题思路Code代码运行结果版权说明<...

ACM第一周---周训---题目合集.
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...

SCI学术论文的基本架构,以及Results、Discussion、Conclusion这三者的区别
SCI论文七大部分,各自应包含哪些内容 SCI写作——论文的结构 一篇SCI论文的大致框架包括Title, Abstract, Introduction, Methods/Methodology, Results, Discussion, Conclusion。不同的学科会有细微的变化,但大体框架基本不变。 1、标题Title 标题用…...

二叉树性质
在二叉树的第i层上至多有2^(i-1)个结点(i≥1)深度为k的二叉树至多有2^k-1个结点(k≥1)对任何一颗二叉树T,如果其叶子数为n0,度为2的结点数位n2,则n0n21满二叉树ÿ…...

二维数组操作示例
给定一个二维字符串数组,求对其按每个一维数组升序排列并按矩阵输出 //创建 String[][] twoDimension {{"A1","A2","A3"},{"B1","B2","B3"}}; List<String> arrayToList null; List<St…...
Spring Boot邮件发送(powernode CD2207)(内含教训视频+源代码)
Spring Boot邮件发送(powernode CD2207)(内含教训视频源代码) 教学视频源代码下载链接地址:https://download.csdn.net/download/weixin_46411355/87452056 目录Spring Boot邮件发送(powernode CD2207&…...

FortiTalk | “三英论安全”之OT安全热门话题解读
OT安全热门话题解读 在数字化转型时代,OT/IT融合已经成为主旋律,可能很多人还没有意识到“工厂”已经不是以前的“工厂”。从封闭走向互联、从现场走向远程、从手动走向自动,这种变革带来的不仅是便捷和效率,更潜藏着巨大的网络安…...
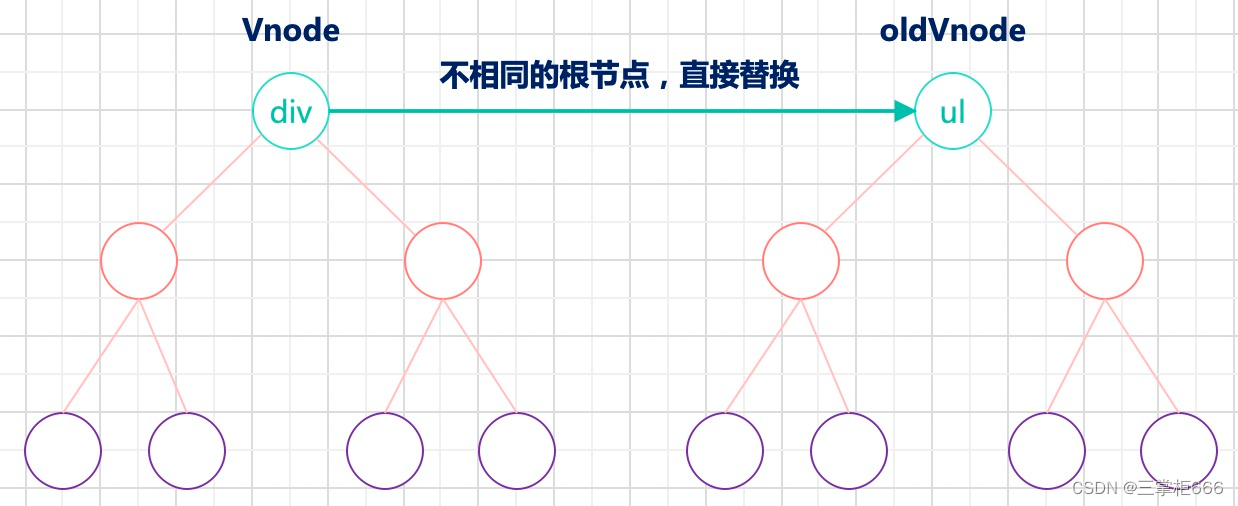
前端开发:关于diff算法详解
前言 前端开发中,关于JS原生的内容和前端算法相关的内容一直都是前端工作中的核心,不管是在实际的前端业务开发还是前端求职面试,都是非常重要且必备的内容。那么本篇博文来分享一个关于前端开发中必备内容:diff算法,d…...
如何为报表开发工具 FastReport .NET 设置 Apache 2 Web 服务器?
FastReport .NET是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。专业版和企业版包括Fast…...
)
华为OD机试真题JAVA实现【出租车计费】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出说明示例二输入输出说明...

MySQL 查看版本的 5 种方法
MySQL 提供了几种用于查看服务器版本的方法,本文给大家做个简单的介绍。 方法一:登录 MySQL 每次通过 mysql 客户端连接服务器之后,都会显示一个欢迎信息,里面包含了服务器的版本: mysql -uroot Enter password: **…...
【软件测试】稳定性测试怎么做,这篇文章彻底讲透了~
稳定性对产品的重要性不言而喻。 而作为质量保障,在稳定性测试方面的探索也在不断演化。记得两年前我们做稳定性测试还是基于恒定的压力,7*24小时长时间运行,关注的指标无非是吞吐量TPS的抖动、响应时间的变化趋势,以及各种资源是…...
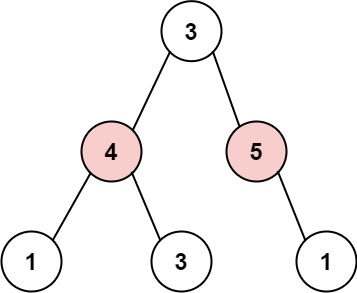
Leetcode:198. 打家劫舍、213. 打家劫舍 II、337. 打家劫舍 III(C++)
目录 198. 打家劫舍 问题描述: 实现代码与解析: 动态规划(版本一): 原理思路: 动态规划(版本二): 原理思路: 213. 打家劫舍 II 问题描述:…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
