机器学习笔记之生成模型综述(五)重参数化技巧(随机反向传播)
机器学习笔记之生成模型综述——重参数化技巧[随机反向传播]
- 引言
- 回顾
- 神经网络的执行过程
- 变分推断——重参数化技巧
- 重参数化技巧(随机反向传播)介绍
- 示例描述——联合概率分布
- 示例描述——条件概率分布
- 总结
引言
本节将系统介绍重参数化技巧。
回顾
神经网络的执行过程
上一节比较了概率图模型与神经网络结构,介绍了它们的各自特点。神经网络(这里指前馈神经网络结构)本质上是一个 函数逼近器:
- 基于一个复杂函数Y=f(X)\mathcal Y = f(\mathcal X)Y=f(X),可通过神经网络进行学习,并对该函数进行近似描述。

- 根据具体任务以及输出信息Y\mathcal YY的性质,去构建对应策略(目标函数/损失函数):
例如线性回归(Linear Regression\text{Linear Regression}Linear Regression)任务中,使用最小二乘估计对预测结果WTx(i)\mathcal W^Tx^{(i)}WTx(i)和真实标签y(i)y^{(i)}y(i)之间的关联关系进行描述:
这里省略了偏置信息bbb,并且(x(i),y(i))(x^{(i)},y^{(i)})(x(i),y(i))是数据集合中的一个样本。
L(W)=∑i=1N∣∣WTx(i)−y(i)∣∣2\mathcal L(\mathcal W) = \sum_{i=1}^N ||\mathcal W^Tx^{(i)} - y^{(i)}||^2L(W)=i=1∑N∣∣WTx(i)−y(i)∣∣2 - 在确定目标函数后,使用梯度下降(Gradient Descent,GD\text{Gradient Descent,GD}Gradient Descent,GD)方法配合反向传播算法(Backward Propagation,BP\text{Backward Propagation,BP}Backward Propagation,BP)对神经网络内部权重、偏置参数进行学习与更新。
变分推断——重参数化技巧
在变分推断——重参数化技巧中,我们同样介绍过重参数化技巧:
- 针对难求解的(Intractable\text{Intractable}Intractable)关于隐变量Z\mathcal ZZ的后验概率分布P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X),通过变分推断(Variational Inference,VI\text{Variational Inference,VI}Variational Inference,VI)的手段,人为定义一个概率分布Q(Z)\mathcal Q(\mathcal Z)Q(Z)去近似P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X):
需要注意的是,这里的Q(Z)\mathcal Q(\mathcal Z)Q(Z)并非指的关于隐变量Z\mathcal ZZ‘边缘概率分布’,而是条件概率分布Q(Z∣X)\mathcal Q(\mathcal Z \mid \mathcal X)Q(Z∣X)缩写而成。
logP(X)=∫ZQ(Z)⋅[P(X,Z)Q(Z)]dZ−∫ZQ(Z)⋅[P(Z∣X)Q(Z)]dZ=ELBO+KL[Q(Z)∣∣P(Z∣X)]\begin{aligned} \log \mathcal P(\mathcal X) & = \int_{\mathcal Z} \mathcal Q(\mathcal Z) \cdot \left[\frac{\mathcal P(\mathcal X,\mathcal Z)}{\mathcal Q(\mathcal Z)}\right] d\mathcal Z - \int_{\mathcal Z} \mathcal Q(\mathcal Z) \cdot \left[\frac{\mathcal P(\mathcal Z \mid \mathcal X)}{\mathcal Q(\mathcal Z)}\right] d\mathcal Z \\ & = \text{ELBO} + \text{KL} [\mathcal Q(\mathcal Z)||\mathcal P(\mathcal Z \mid \mathcal X)] \\ \end{aligned}logP(X)=∫ZQ(Z)⋅[Q(Z)P(X,Z)]dZ−∫ZQ(Z)⋅[Q(Z)P(Z∣X)]dZ=ELBO+KL[Q(Z)∣∣P(Z∣X)] - 将证据下界(Evidence of Lower Bound,ELBO\text{Evidence of Lower Bound,ELBO}Evidence of Lower Bound,ELBO)看作关于Q(Z)\mathcal Q(\mathcal Z)Q(Z)的一个函数。称作Q(Z)\mathcal Q(\mathcal Z)Q(Z)的变分(Variation\text{Variation}Variation)。记作L[Q(Z)]\mathcal L[\mathcal Q(\mathcal Z)]L[Q(Z)]:
ELBO=∫ZQ(Z)⋅[P(X,Z)Q(Z)]dZ=L[Q(Z)]\begin{aligned} \text{ELBO} = \int_{\mathcal Z} \mathcal Q(\mathcal Z) \cdot \left[\frac{\mathcal P(\mathcal X,\mathcal Z)}{\mathcal Q(\mathcal Z)}\right] d\mathcal Z = \mathcal L[\mathcal Q(\mathcal Z)] \end{aligned}ELBO=∫ZQ(Z)⋅[Q(Z)P(X,Z)]dZ=L[Q(Z)] - 在随机梯度变分推断(Stochastic Gradient Variational Inference, SGVI\text{Stochastic Gradient Variational Inference, SGVI}Stochastic Gradient Variational Inference, SGVI)的思路中,将条件概率分布Q(Z)\mathcal Q(\mathcal Z)Q(Z)视作一个关于参数ϕ\phiϕ的函数形式Q(Z;ϕ)\mathcal Q(\mathcal Z;\phi)Q(Z;ϕ),那么对应变分L[Q(Z)]\mathcal L[\mathcal Q(\mathcal Z)]L[Q(Z)]也可描述成关于ϕ\phiϕ的函数形式:
此时将求解分布Q(Z)\mathcal Q(\mathcal Z)Q(Z)的问题转化为求解最优参数ϕ^\hat \phiϕ^的问题。
L[Q(Z)]=L[Q(Z;ϕ)]⇒L(ϕ)\mathcal L[\mathcal Q(\mathcal Z)] = \mathcal L[\mathcal Q(\mathcal Z;\phi)] \Rightarrow \mathcal L(\phi)L[Q(Z)]=L[Q(Z;ϕ)]⇒L(ϕ)
基于L(ϕ)\mathcal L(\phi)L(ϕ)求解最大值,使用梯度上升(Gradient Ascent,GA\text{Gradient Ascent,GA}Gradient Ascent,GA)方法近似求解。对应函数梯度表示如下:
{ϕ(t+1)⇐ϕ(t)+η∇ϕL(ϕ)∇ϕL(ϕ)=EQ(Z;ϕ){∇ϕlogQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}\begin{cases} \phi^{(t+1)} \Leftarrow \phi^{(t)} + \eta \nabla_{\phi} \mathcal L(\phi) \\ \nabla_{\phi} \mathcal L(\phi) = \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left\{\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi) \cdot [\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)] \right\} \end{cases}{ϕ(t+1)⇐ϕ(t)+η∇ϕL(ϕ)∇ϕL(ϕ)=EQ(Z;ϕ){∇ϕlogQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]} - 在使用蒙特卡洛方法进行采样近似过程中,关于∇ϕlogQ(Z;ϕ)\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi)∇ϕlogQ(Z;ϕ)极容易出现高方差现象(High Variance\text{High Variance}High Variance),导致采样出的梯度结果∇ϕL(ϕ)\nabla_{\phi} \mathcal L(\phi)∇ϕL(ϕ)极不稳定:
∇ϕL(ϕ)≈1N∑n=1N{∇ϕlogQ(z(n);ϕ)⏟High Variance[logP(X,z(n))−logQ(z(n);ϕ)]}\nabla_{\phi}\mathcal L(\phi) \approx \frac{1}{N} \sum_{n=1}^N \left\{\underbrace{\nabla_{\phi} \log \mathcal Q(z^{(n)};\phi)}_{\text{High Variance}} \left[\log \mathcal P(\mathcal X,z^{(n)}) - \log \mathcal Q(z^{(n)};\phi)\right]\right\}∇ϕL(ϕ)≈N1n=1∑N⎩⎨⎧High Variance∇ϕlogQ(z(n);ϕ)[logP(X,z(n))−logQ(z(n);ϕ)]⎭⎬⎫
针对已经被视作函数的Q(Z;ϕ)\mathcal Q(\mathcal Z;\phi)Q(Z;ϕ),通过重参数化技巧,通过构建一个 随机变量ϵ\epsilonϵ,使得ϵ\epsilonϵ与隐变量Z\mathcal ZZ之间存在如下函数关系:
Z=G(ϵ,X;ϕ)\mathcal Z = \mathcal G(\epsilon,\mathcal X ;\phi)Z=G(ϵ,X;ϕ)
从而使得ϵ\epsilonϵ对应的概率分布P(ϵ)\mathcal P(\epsilon)P(ϵ)与分布Q(Z;ϕ)\mathcal Q(\mathcal Z;\phi)Q(Z;ϕ)之间存在如下关系:
EQ(Z;ϕ)[f(Z)]=EP(ϵ){f[G(ϵ,X;ϕ)]}\mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left[f(\mathcal Z)\right] = \mathbb E_{\mathcal P(\epsilon)} \left\{f[\mathcal G(\epsilon,\mathcal X;\phi)]\right\}EQ(Z;ϕ)[f(Z)]=EP(ϵ){f[G(ϵ,X;ϕ)]}
将上述关系带回原式,通过链式求导法则,可以表示成如下形式:将期望形式化简回积分形式。牛顿-莱布尼兹公式,将∇ϕ\nabla_{\phi}∇ϕ提到积分号前,后面再带回去。将Z=G(ϵ,X;ϕ)\mathcal Z = \mathcal G(\epsilon,\mathcal X;\phi)Z=G(ϵ,X;ϕ)代入,并将采样分布Q(Z;ϕ)\mathcal Q(\mathcal Z;\phi)Q(Z;ϕ)替换为P(ϵ)\mathcal P(\epsilon)P(ϵ).
∇ϕL(ϕ)=EQ(Z;ϕ){∇ϕlogQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}=∇ϕ∫ZQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]dZ=EP(ϵ)[∇ϕ(logP(X,Z)−logQ(Z;ϕ))]=EP(ϵ)[∇Z(logP(X,Z)−logQ(Z;ϕ))⋅∇ϕG(ϵ,X;ϕ)]\begin{aligned} \nabla_{\phi}\mathcal L(\phi) & = \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left\{\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi) \cdot [\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)] \right\} \\ & = \nabla_{\phi} \int_{\mathcal Z} \mathcal Q(\mathcal Z;\phi) \cdot \left[\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)\right] d\mathcal Z \\ & = \mathbb E_{\mathcal P(\epsilon)} \left[\nabla_{\phi}(\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi))\right] \\ & = \mathbb E_{\mathcal P(\epsilon)} [\nabla_{\mathcal Z}(\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)) \cdot \nabla_{\phi}\mathcal G(\epsilon,\mathcal X;\phi)] \end{aligned}∇ϕL(ϕ)=EQ(Z;ϕ){∇ϕlogQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}=∇ϕ∫ZQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]dZ=EP(ϵ)[∇ϕ(logP(X,Z)−logQ(Z;ϕ))]=EP(ϵ)[∇Z(logP(X,Z)−logQ(Z;ϕ))⋅∇ϕG(ϵ,X;ϕ)]
通过这种重参数化技巧——将 变量Z\mathcal ZZ 与 简单分布对应变量ϵ\epsilonϵ 之间构建关联关系的方式,仅需要从简单分布P(ϵ)\mathcal P(\epsilon)P(ϵ)中进行采样,也可以采集出∇ϕL(ϕ)\nabla_{\phi}\mathcal L(\phi)∇ϕL(ϕ)中的样本。
重参数化技巧(随机反向传播)介绍
关于神经网络,可以通过通用逼近定理(Universal Approximation Theorem\text{Universal Approximation Theorem}Universal Approximation Theorem)来逼近任意函数。那么神经网络是否也可以用来 逼近概率分布 呢?
从概率图模型的视角,概率分布P(X)\mathcal P(\mathcal X)P(X)就是概率图模型结构的表示(Representation\text{Representation}Representation)。如果能够直接使用神经网络直接将P(X)\mathcal P(\mathcal X)P(X)描述出来,就称之为随机反向传播(Stochastic Backward Propagation\text{Stochastic Backward Propagation}Stochastic Backward Propagation),也称重参数化技巧(Reparametrization Trick\text{Reparametrization Trick}Reparametrization Trick)。
在上面关于变分推断——重参数化技巧的过程中,关于Z=G(ϵ,X;ϕ)\mathcal Z = \mathcal G(\epsilon,\mathcal X;\phi)Z=G(ϵ,X;ϕ)中的函数G\mathcal GG,同样可以描述成如下结构:
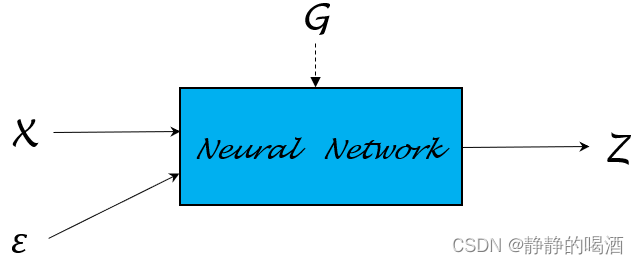
这里从简单的概率分布开始,观察如何使用重参数化技巧对概率分布进行描述的。
示例描述——联合概率分布
假设某随机变量Y\mathcal YY服从均值为μ\muμ,方差为σ2\sigma^2σ2的一维正态分布:
P(Y)=N(μ,σ2)\mathcal P(\mathcal Y) = \mathcal N(\mu,\sigma^2)P(Y)=N(μ,σ2)
如果直接从这个分布中进行采样,可能是复杂的。但是如果可以假定一个变量Z\mathcal ZZ服从标准正态分布N(0,1)\mathcal N(0,1)N(0,1),并且Y,Z\mathcal Y,\mathcal ZY,Z之间满足如下关系:
Y=μ+σ×Z\mathcal Y = \mu + \sigma \times \mathcal ZY=μ+σ×Z
那么则有:
该部分推导过程详见:变分推断——重参数化技巧
EP(Y)[f(Y)]=EP(Z)[f(μ+σ×Z)]\mathbb E_{\mathcal P(\mathcal Y)} [f(\mathcal Y)] = \mathbb E_{\mathcal P(\mathcal Z)} [f(\mu + \sigma \times \mathcal Z)]EP(Y)[f(Y)]=EP(Z)[f(μ+σ×Z)]
这种替换采样分布的操作意味着:在给定Z\mathcal ZZ分布的条件下,完全可以通过采样Z\mathcal ZZ分布,得到Y\mathcal YY分布的样本:
这里的Z(i),Y(i)\mathcal Z^{(i)},\mathcal Y^{(i)}Z(i),Y(i)分别表示概率分布P(Z),P(Y)\mathcal P(\mathcal Z),\mathcal P(\mathcal Y)P(Z),P(Y)中采集的样本。
{Z(i)∼N(0,1)Y(i)=μ+σ×Z(i)\begin{cases} \mathcal Z^{(i)} \sim \mathcal N(0,1) \\ \mathcal Y^{(i)} = \mu + \sigma \times \mathcal Z^{(i)} \end{cases}{Z(i)∼N(0,1)Y(i)=μ+σ×Z(i)
重新观察Y=μ+σ×Z\mathcal Y = \mu + \sigma \times \mathcal ZY=μ+σ×Z,这明显就是一个简单的一次函数。从广义的角度观察,可以将Y,Z\mathcal Y,\mathcal ZY,Z之间满足如下函数关系:
其中Z\mathcal ZZ在函数中表示变量;μ,σ\mu,\sigmaμ,σ在函数中表示权重参数。
Y=f(Z;μ,σ)\mathcal Y = f(\mathcal Z;\mu,\sigma)Y=f(Z;μ,σ)
这意味着:我们不否认变量Y\mathcal YY具有随机性,只不过变量Y\mathcal YY的随机性由变量Z\mathcal ZZ决定。也就是说,除了Z\mathcal ZZ的随机性,其他变量(这里指的Y\mathcal YY)都是确定性变换,那么完全可以使用神经网络对函数f(Z;μ,σ)f(\mathcal Z;\mu,\sigma)f(Z;μ,σ)进行逼近:
这里的‘确定性变换’是指:当变量Z\mathcal ZZ确定的条件下,那么变量Y\mathcal YY根据函数f(Z;μ,σ)f(\mathcal Z;\mu,\sigma)f(Z;μ,σ)也跟着确定。也就是说Z,Y\mathcal Z,\mathcal YZ,Y之间存在明确的映射关系。使用神经网络逼近函数,完全不用担心原始函数中的参数μ,σ\mu,\sigmaμ,σ,因为被替代的神经网络权重参数θ\thetaθ本身没有实际意义。
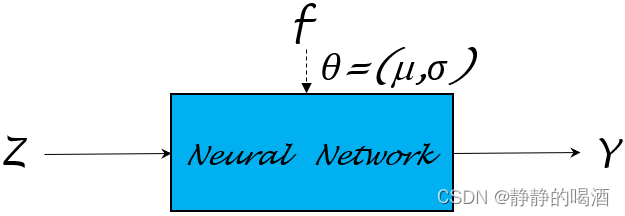
如果定义J(Y)\mathcal J(\mathcal Y)J(Y)为目标函数,在对目标函数求解极值的过程中,对模型参数θ\thetaθ求解梯度。根据链式求导法则,梯度∇θJ(Y)\nabla_{\theta}\mathcal J(\mathcal Y)∇θJ(Y) 可表示为如下形式:
{J(Y)=J[f(Z;μ,σ)]∇θJ(Y)=∇YJ(Y)⋅∇θf(Z;μ,σ)\begin{cases} \mathcal J(\mathcal Y) = \mathcal J[f(\mathcal Z;\mu,\sigma)] \\ \nabla_{\theta} \mathcal J(\mathcal Y) = \nabla_{\mathcal Y} \mathcal J(\mathcal Y) \cdot \nabla_{\theta}f(\mathcal Z;\mu,\sigma) \end{cases}{J(Y)=J[f(Z;μ,σ)]∇θJ(Y)=∇YJ(Y)⋅∇θf(Z;μ,σ)
示例描述——条件概率分布
假设给定随机变量X\mathcal XX条件下,随机变量Y\mathcal YY的条件概率分布满足如下关系:
P(Y∣X)=N(μ,σ2∣X)\mathcal P(\mathcal Y \mid \mathcal X) = \mathcal N(\mu,\sigma^2 \mid \mathcal X)P(Y∣X)=N(μ,σ2∣X)
与上面描述对应,可以根据分布N(μ,σ2∣X)\mathcal N(\mu,\sigma^2 \mid \mathcal X)N(μ,σ2∣X),可以将随机变量Y\mathcal YY与随机变量X\mathcal XX之间描述成如下函数关系:
{Z∼N(0,1)Y=μ(X)+σ(X)×Z\begin{cases} \mathcal Z \sim \mathcal N(0,1) \\ \mathcal Y = \mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z \end{cases}{Z∼N(0,1)Y=μ(X)+σ(X)×Z
同样可以使用上述方法,对随机变量Y\mathcal YY与随机变量Z\mathcal ZZ之间的关系进行验证:
关键点1:从概率密度函数的角度观察,由于X\mathcal XX是条件,是已知量。因而可以将N(μ,σ2∣X)\mathcal N(\mu,\sigma^2 \mid \mathcal X)N(μ,σ2∣X)看作是随机变量X\mathcal XX参与的概率密度函数:N[μ(X),σ2(X)]\mathcal N[\mu(\mathcal X),\sigma^2(\mathcal X)]N[μ(X),σ2(X)]证明期望EP(Y∣X)[f(Y)]\mathbb E_{\mathcal P(\mathcal Y \mid \mathcal X)} [f(\mathcal Y)]EP(Y∣X)[f(Y)]转换成期望EP(Z){f[μ(X)+σ(X)×Z]}\mathbb E_{\mathcal P(\mathcal Z)} \{f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z]\}EP(Z){f[μ(X)+σ(X)×Z]}的过程实际上是描述Y\mathcal YY被替换成μ(X)+σ(X)×Z\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Zμ(X)+σ(X)×Z后,其采样分布也会由P(Y∣X)\mathcal P(\mathcal Y \mid \mathcal X)P(Y∣X)转换成P(Z)\mathcal P(\mathcal Z)P(Z),而不仅仅是单纯意义上的替换。关键点2:将Y=μ(X)+σ(X)×Z\mathcal Y = \mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal ZY=μ(X)+σ(X)×Z代入的过程中,由于是对Z\mathcal ZZ求解偏导,因而有dY=d[μ(X)+σ(X)×Z]=σ(X)dZd\mathcal Y = d[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] = \sigma(\mathcal X) d\mathcal ZdY=d[μ(X)+σ(X)×Z]=σ(X)dZ
EP(Y∣X)[f(Y)]=∫YP(Y∣X)⋅f(Y)dY=∫Y1σ(X)⋅2πexp{−[Y−μ(X)]22σ2(X)}⏟N[μ(X),σ2(X)]⋅f(Y)dY=∫Z1σ(X)⋅2πexp{−[μ(X)+σ(X)×Z−μ(X)]22σ2(X)}⋅f[μ(X)+σ(X)×Z]⋅σ(X)dZ⏟d[μ(X)+σ(X)×Z]=∫Z12π⋅exp(−Z22)⏟P(Z)=N(0,1)⋅f[μ(X)+σ(X)×Z]dZ=∫ZP(Z)⋅f[μ(X)+σ(X)×Z]dZ=EP(Z){f[μ(X)+σ(X)×Z]}\begin{aligned} \mathbb E_{\mathcal P(\mathcal Y \mid \mathcal X)} [f(\mathcal Y)] & = \int_{\mathcal Y} \mathcal P(\mathcal Y \mid \mathcal X) \cdot f(\mathcal Y) d\mathcal Y \\ & = \int_{\mathcal Y} \underbrace{\frac{1}{\sigma(\mathcal X) \cdot \sqrt{2\pi}}\exp \left\{-\frac{[\mathcal Y - \mu(\mathcal X)]^2}{2\sigma^2(\mathcal X)}\right\}}_{\mathcal N[\mu(\mathcal X),\sigma^2(\mathcal X)]} \cdot f(\mathcal Y) d\mathcal Y \\ & = \int_\mathcal Z \frac{1}{\sigma(\mathcal X) \cdot \sqrt{2\pi}} \exp \left\{-\frac{[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z - \mu(\mathcal X)]^2}{2\sigma^2(\mathcal X)}\right\} \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] \cdot \underbrace{\sigma(\mathcal X) d\mathcal Z}_{d[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z]} \\ & = \int_{\mathcal Z} \underbrace{\frac{1}{\sqrt{2\pi}} \cdot \exp \left(-\frac{\mathcal Z^2}{2}\right)}_{\mathcal P(\mathcal Z) = \mathcal N(0,1)} \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] d\mathcal Z \\ & = \int_{\mathcal Z}\mathcal P(\mathcal Z) \cdot f[\mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal Z] d\mathcal Z \\ & = \mathbb E_{\mathcal P(\mathcal Z)} \{f[\mu(\mathcal X) +\sigma(\mathcal X) \times \mathcal Z]\} \end{aligned}EP(Y∣X)[f(Y)]=∫YP(Y∣X)⋅f(Y)dY=∫YN[μ(X),σ2(X)]σ(X)⋅2π1exp{−2σ2(X)[Y−μ(X)]2}⋅f(Y)dY=∫Zσ(X)⋅2π1exp{−2σ2(X)[μ(X)+σ(X)×Z−μ(X)]2}⋅f[μ(X)+σ(X)×Z]⋅d[μ(X)+σ(X)×Z]σ(X)dZ=∫ZP(Z)=N(0,1)2π1⋅exp(−2Z2)⋅f[μ(X)+σ(X)×Z]dZ=∫ZP(Z)⋅f[μ(X)+σ(X)×Z]dZ=EP(Z){f[μ(X)+σ(X)×Z]}
同理,基于上述的神经网络描述,同样也可以随机变量X,Z∼N(0,1)\mathcal X,\mathcal Z \sim \mathcal N(0,1)X,Z∼N(0,1)为输入,Y\mathcal YY作为输出,学习并逼近函数Y=μ(X)+σ(X)×Z\mathcal Y = \mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal ZY=μ(X)+σ(X)×Z:
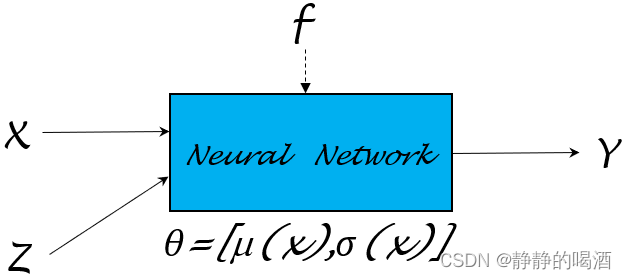
继续向下观察。从Y=μ(X)+σ(X)×Z\mathcal Y = \mu(\mathcal X) + \sigma(\mathcal X) \times \mathcal ZY=μ(X)+σ(X)×Z中可以观察到:
- Y\mathcal YY是关于Z\mathcal ZZ的函数,其中参数是μ(X),σ(X)\mu(\mathcal X),\sigma(\mathcal X)μ(X),σ(X);
- 而μ,σ\mu,\sigmaμ,σ均是关于X\mathcal XX的函数。
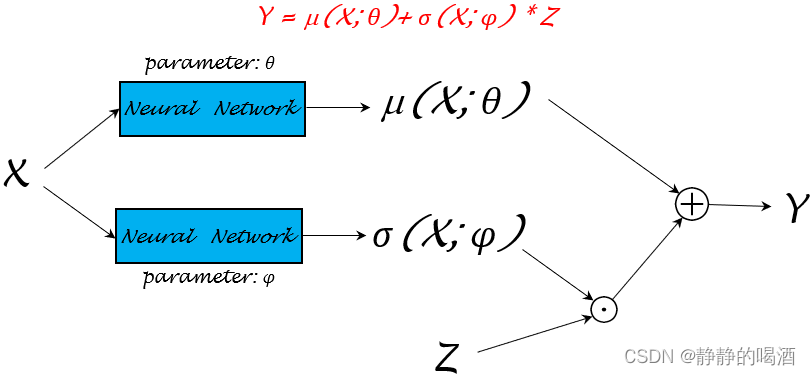
既然μ,σ\mu,\sigmaμ,σ函数均以随机变量X\mathcal XX作为输入,这里将这两个函数的参数统一描述成θ\thetaθ。即:μ(X;θ),σ(X;θ)\mu(\mathcal X;\theta),\sigma(\mathcal X;\theta)μ(X;θ),σ(X;θ)。这种变换意味着:仅通过学习模型参数θ\thetaθ,就可以将μ(X),σ(X)\mu(\mathcal X),\sigma(\mathcal X)μ(X),σ(X)均给表示出来。上述神经网络结构可细化成如下形式:
其中⊙\odot⊙表示点乘;⊕\oplus⊕表示数学加法。
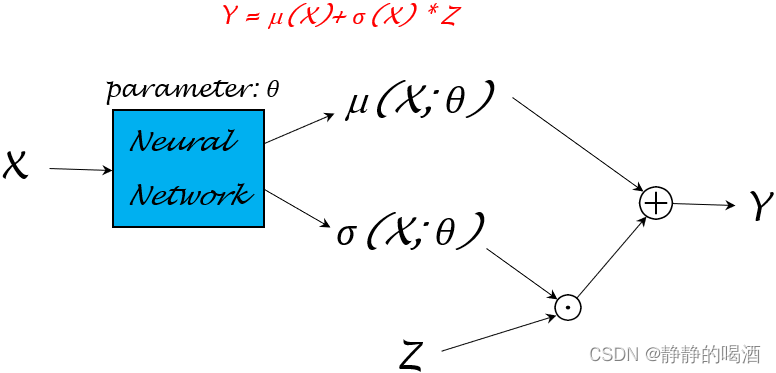
关于模型参数θ\thetaθ的参数学习过程可以很灵活。关于函数μ(X),σ(X)\mu(\mathcal X),\sigma(\mathcal X)μ(X),σ(X)可以再详细分成不同的模型参数μ(X;θ),σ(X;ϕ)\mu(\mathcal X;\theta),\sigma(\mathcal X;\phi)μ(X;θ),σ(X;ϕ)进行学习:
神经网络仅是一个‘函数逼近器’的作用,如何将模型参数学习的更好,可以有很深的挖掘空间。只不过这里我们事先知道Y\mathcal YY的分布是N(μ,σ∣X)\mathcal N(\mu,\sigma\mid \mathcal X)N(μ,σ∣X),这里的μ,σ\mu,\sigmaμ,σ被赋予了实际意义。但真实情况是,这个条件概率分布Y\mathcal YY可能非常复杂。我们对模型参数组成可能一无所知。
同样可以构建一个目标函数J(Y)\mathcal J(\mathcal Y)J(Y),通过链式求导法则,将对应的模型参数梯度进行求解。
示例:如果通过重参数化技巧产生样本所代表的概率分布Ypred\mathcal Y_{pred}Ypred与真实分布Y\mathcal YY之间的差距(可以看成一个基于分布的回归任务),可以通过最小二乘估计对差距进行描述:
这里以第一种模型结构为例。其中Ygene(i)\mathcal Y_{gene}^{(i)}Ygene(i)就是图中Y\mathcal YY通过上述模型结构产生的一个样本(幻想粒子),与对应真实分布中的Y(i)\mathcal Y^{(i)}Y(i)样本进行比较。
J(Ygene;θ)=∑i=1N∣∣Ygene(i)−Y(i)∣∣2\mathcal J(\mathcal Y_{gene};\theta) = \sum_{i=1}^N ||\mathcal Y_{gene}^{(i)} - \mathcal Y^{(i)}||^2J(Ygene;θ)=i=1∑N∣∣Ygene(i)−Y(i)∣∣2
对应梯度∇θJ(Ygene;θ)\nabla_{\theta}\mathcal J(\mathcal Y_{gene};\theta)∇θJ(Ygene;θ)可表示为:
∇θJ(Ygene;θ)=∂J(Ygene;θ)∂Ygene⋅∂Ygene∂μ(X;θ)⋅∂μ(X;θ)∂θ+∂J(Ygene;θ)∂Ygene⋅∂Ygene∂σ(X;θ)⋅∂σ(X;θ)∂θ\nabla_{\theta} \mathcal J(\mathcal Y_{gene};\theta) = \begin{aligned} \frac{\partial \mathcal J(\mathcal Y_{gene};\theta)}{\partial \mathcal Y_{gene}} \cdot \frac{\partial \mathcal Y_{gene}}{\partial \mu(\mathcal X;\theta)} \cdot \frac{\partial \mu(\mathcal X;\theta)}{\partial \theta} + \frac{\partial \mathcal J(\mathcal Y_{gene};\theta)}{\partial \mathcal Y_{gene}} \cdot \frac{\partial \mathcal Y_{gene}}{\partial \sigma(\mathcal X;\theta)} \cdot \frac{\partial \sigma(\mathcal X;\theta)}{\partial \theta} \end{aligned} ∇θJ(Ygene;θ)=∂Ygene∂J(Ygene;θ)⋅∂μ(X;θ)∂Ygene⋅∂θ∂μ(X;θ)+∂Ygene∂J(Ygene;θ)⋅∂σ(X;θ)∂Ygene⋅∂θ∂σ(X;θ)
总结
通过上面的描述,通过重参数化技巧构造神经网络去逼近联合概率分布、条件概率分布。关于这种表示方式,对于生成分布Y\mathcal YY是存在约束条件的。即:Y\mathcal YY是一个 连续分布。这才能使∂Ygene∂μ(X;θ),∂Ygene∂σ(X;θ)\frac{\partial \mathcal Y_{gene}}{\partial \mu(\mathcal X;\theta)},\frac{\partial \mathcal Y_{gene}}{\partial \sigma(\mathcal X;\theta)}∂μ(X;θ)∂Ygene,∂σ(X;θ)∂Ygene有解。
至此,生成模型部分介绍结束,下一节将介绍流模型(Flow-based Model\text{Flow-based Model}Flow-based Model)。
相关参考:
生成模型6-重参数化技巧(随机后向传播)
相关文章:

机器学习笔记之生成模型综述(五)重参数化技巧(随机反向传播)
机器学习笔记之生成模型综述——重参数化技巧[随机反向传播]引言回顾神经网络的执行过程变分推断——重参数化技巧重参数化技巧(随机反向传播)介绍示例描述——联合概率分布示例描述——条件概率分布总结引言 本节将系统介绍重参数化技巧。 回顾 神经网络的执行过程 上一节…...
1、创建第一个Android项目
1.1、创建Android工程项目:双击打开Android Studio。在菜单栏File中new-->new project3、在界面中选择Empty Activity,然后选择next4、在下面界面中修改工程名称,工程保存路径选择java语言,然后点击finishAndroid studio自动为…...
【python百炼成魔】手把手带你学会python数据类型
文章目录前言一. python的基本数据类型1.1 如何查看数据类型1.2 数值数据类型1.2.1 整数类型1.2.2 浮点数类型1.2.3 bool 布尔数值类型1.2.4 字符串类型二. 数据类型强制转换2.1 强制转换为字符串类型2.2 强制转换为int类型2.3 强制转换函数之float() 函数三. 拓展几个运算函数…...
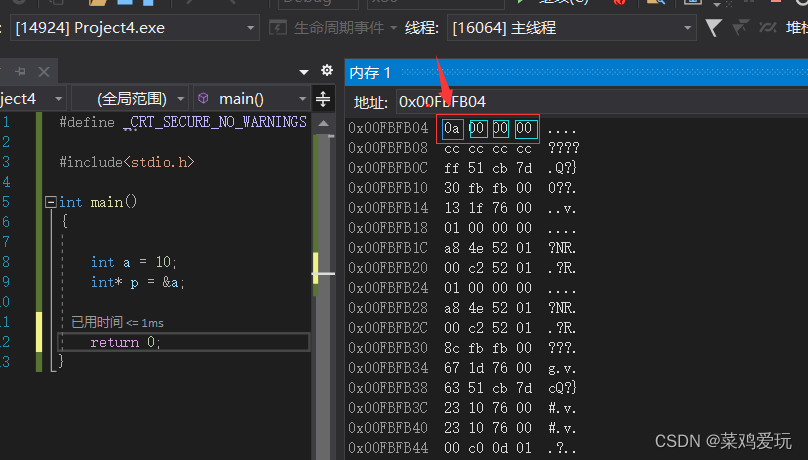
数据储存以及大小端判断
目录 数据存储 1,二进制存储方式(补码,反码,源码) 2,指针类型 3,大端,小段判断 1,二进制存储方式(补码,反码,源码) 我…...

GRASP设计原则
GRASP设计原则介绍9种基本原则创建者 Creator问题解决方法何时不使用?好处信息专家 Information Expert问题解决方法信息怎么做优点低耦合 Low Coupling耦合问题解决方法原则何时不使用?控制器 Controller问题解决方法外观控制器会话控制器优点臃肿控制器的解决方法高内聚 Hi…...

再遇周杰伦隐私协议
本隐私信息保护政策版本:2021 V1 一、重要提示 请您(以下亦称“用户”)在使用本平台App时仔细阅读本协议之全部条款,并确认您已完全理解本协议之规定,尤其是涉及您的重大权益及义务的加粗或划线条款。如您对协议有任…...

关于项目上的一些小操作记录
一 如何在项目的readme.md文件中插入图片说明 1 准备一张图片命名为test.png 2 在maven项目的resources目录下新建文件夹picture,将图片放入该目录下 3 在readme.md文件中期望插入图片的地方编辑如下:  此时&#…...
)
sql查询不以某些指定字符开头(正则表达式)
我们用到的最多的是:查询以特定字符或字符串开头的记录 字符^用来匹配以特定字符或字符串开头的记录。 例 1 在 tb_students_info 表中,查询 name 字段以“J”开头的记录,SQL 语句和执行过程如下。 mysql> SELECT * FROM tb_students_…...
35.网络结构与模型压缩、加速-2
35.1 Depthwise separable convolution Depthwise separable convolution是由depthwise conv和pointwise conv构成depthwise conv(DW)有效减少参数数量并提升运算速度 但是由于每个feature map只被一个卷积核卷积,因此经过DW输出的feature map不能只包含输入特征图的全部信息,…...
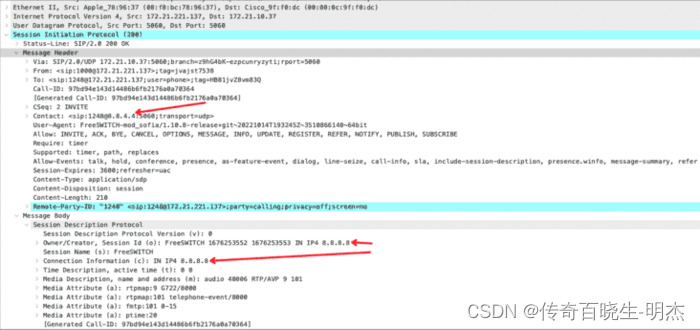
FreeSWITCH跨NAT部署配置详解
本文仅讨论FreeSWITCH部署在NAT之后(里面)这种场景,假设私网地址与公网地址有一个确定的映射关系。这里只涉及mod_sofia(SIP信令及媒体)相关配置,其他模块不在本文讨论之列。配置mod_sofia默认提供两个prof…...
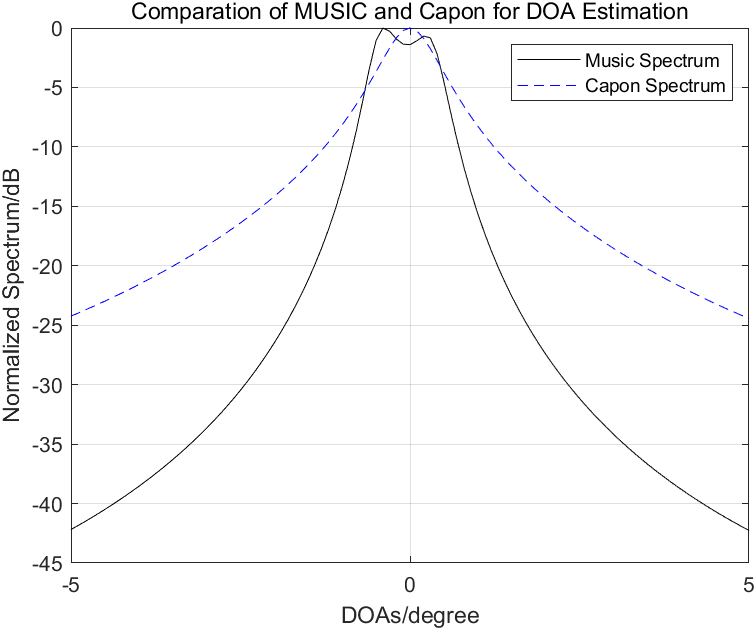
【精选论文 | Capon算法与MUSIC算法性能的比较与分析】
本文编辑:调皮哥的小助理 【正文】 首先说结论: 当信噪比(SNR)足够大时,Capon算法和MUSIC算法的空间谱非常相似,因此在SNR比较大时它们的性能几乎一样,当不同信号源的入射角度比较接近时&…...
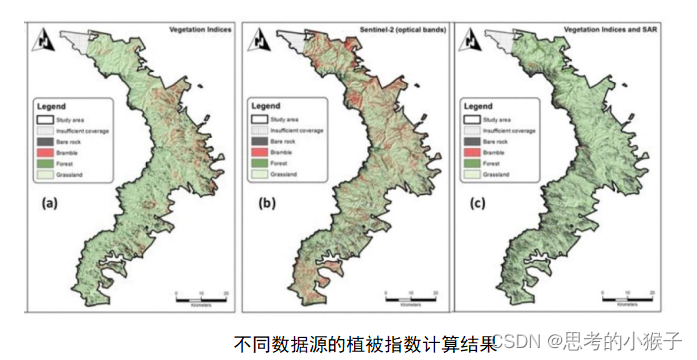
卫星、无人机平台的多光谱数据在地质、土壤调查和农业等需要用什么?
近年来,Python编程语言受到越来越多科研人员的喜爱,在多个编程语言排行榜中持续夺冠。同时,伴随着深度学习的快速发展,人工智能技术在各个领域中的应用越来越广泛。机器学习是人工智能的基础,因此,掌握常用…...
30个题型+代码(冲刺2023蓝桥杯)
愿意的可以跟我一起刷,每个类型做1~5题 ,4月前还可以回来系统复习 2月13日 ~ 3月28日,一共32天 一个月时间,0基础省三 --> 省二;基础好点的,省二 --> 省一 目录 🌼前言 🌼…...
快速且有效减小代码包的方法
前言当我们在发布一些APP或者小程序等比较小的程序时候,常常会对其主包大小进行一定的规定,若超过推荐的主包大小则性能会被大大影响,或者再严重一点就不给你过审。如微信小程序中也对主包有一定的大小要求。对此一些比较复杂的小程序就需要考…...

基于matlab评估星载合成孔径雷达性能
一、前言本示例展示了如何评估星载合成孔径雷达 (SAR) 的性能,并将理论极限与 SAR 系统的可实现要求进行比较。SAR利用雷达天线在目标区域上的运动来提供更精细的方位角分辨率。给定雷达的主要参数(例如工作频率、天线尺寸和带宽&…...

Linux_基本指令
新的专栏Linux入门来啦!欢迎各位大佬补充指正!! Linux_基本指令导入文件绝对路径与相对路径隐藏的文件指令ls查看stat查看文件属性cd进入路径mkdir创建目录touch创建文件rm删除man查询手册cp复制mv移动cat查看文件morelessheadtail时间相关的…...

Keras深度学习实战——使用深度Q学习进行SpaceInvaders游戏
Keras深度学习实战——使用深度Q学习进行SpaceInvaders游戏 0. 前言1. 问题与模型分析2. 使用深度 Q 学习进行 SpaceInvaders 游戏相关链接0. 前言 在《深度Q学习算法详解》一节中,我们使用了深度 Q 学习来进行 Cart-Pole 游戏。在本节中,我们将利用深度Q学习来玩“太空侵略…...
从事架构师岗位快2年了,聊一聊我对架构的一些感受和看法
从事架构师岗位快2年了,聊一聊我和ChatGPT对架构的一些感受和看法 职位不分高低,但求每天都能有新的进步,永远向着更高的目标前进。 文章目录踏上新的征程架构是什么?架构师到底是干什么的?你的终极目标又是什么&#…...

零基础机器学习做游戏辅助第十二课--原神自动钓鱼(二)
一、模拟训练环境 上节课我们已经能够判断人物的钓鱼状态,接下来我们就需要对鱼儿上钩后的那个受力框进行DQN训练。 方案有两个: 使用卷积神经网络直接输入图像对网络进行训练。使用普通网络,自己写代码模拟出图像中三个点的动态并把值给神经网络进行训练。这里我们选用第二…...
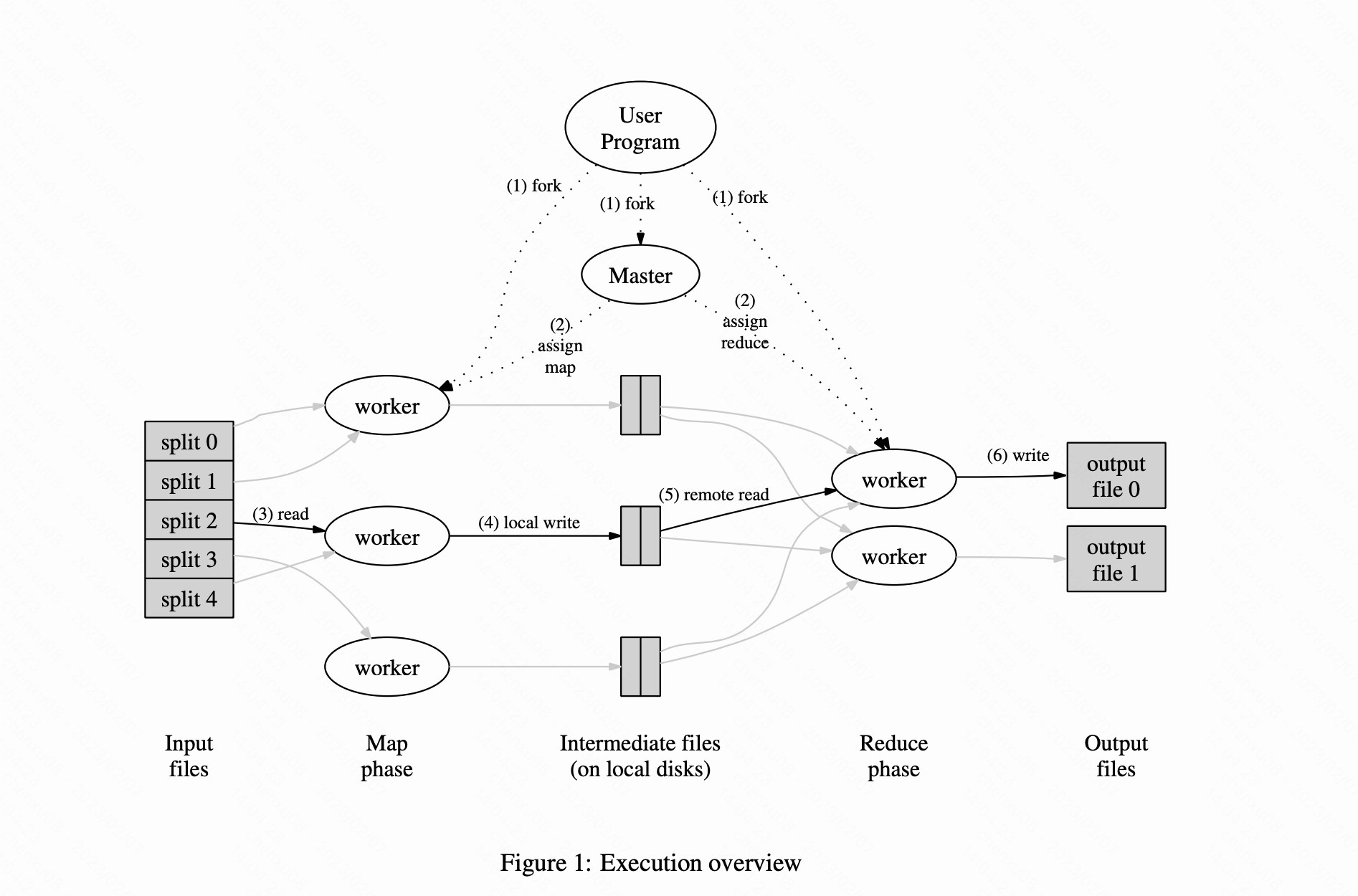
MapReduce paper(2004)-阅读笔记
文章目录前言摘要(Abstract)一、引言( Introduction)二、编程模型(Programming Model)三、实现(Implementation)3.1、执行概述(Execution Overview)3.2、主节点数据结构(Master Data…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
