【精选论文 | Capon算法与MUSIC算法性能的比较与分析】
本文编辑:调皮哥的小助理

【正文】
首先说结论:
当信噪比(SNR)足够大时,Capon算法和MUSIC算法的空间谱非常相似,因此在SNR比较大时它们的性能几乎一样,当不同信号源的入射角度比较接近时,MUSIC算法的性能优于Capon,这也是MUSIC算法(或者说子空间类算法)被称为高分辨率算法的原因。
原文:On one hand, if the SNR is large enough, the spectrums of Capon and MUSIC are approximately the same, and hence their performances may be similar. On the other hand, MUSIC algorithm performs better than Capon algorithm when the separation angle of sources is quite small, and this is why MUSIC (or saying subspace-based methods) is called as high-resolution algorithm.
这个结论要记住,记得这个问题之前找工作被面试官问过。
下面我们会用论文《The Difference Between Capon and MUSIC Algorithm》中的内容论述这个结论,并给出仿真示例。
1、Capon算法原理
Capon是一位科学家的名字,因为他提出了Capon这种算法,是以他的名字来命名的。我们将数据模型考虑为:
x(t)=As(t)+n(t)\mathbf{x}(t)=\mathbf{A} \mathbf{s}(t)+\mathbf{n}(t)x(t)=As(t)+n(t)(1)
其中,x(t)是观测数据向量,A是阵列信号处理中所谓的导向矩阵,s(t)和n(t)分别代表信号和噪声向量,t表示时间索引。将一个权重向量w放到观察向量x(t)上,我们得到的输出为:
y(t)=wHx(t)y(t)=\mathbf{w}^H \mathbf{x}(t)y(t)=wHx(t)(2)
因此,阵列输出的功率可以公式化如下:
Ry=E{∣y(t)∣2}=wHRxwR_y=\mathrm{E}\left\{|y(t)|^2\right\}=\mathbf{w}^H \mathbf{R}_{\mathbf{x}} \mathbf{w}Ry=E{∣y(t)∣2}=wHRxw(3)
其中E{·}和·H分别表示数学期望和埃尔米特转置。此外,Rx=E{x(t)xH(t)}\mathbf{R}_{\mathbf{x}}=\mathrm{E}\left\{\mathbf{x}(t) \mathbf{x}^H(t)\right\}Rx=E{x(t)xH(t)} 是观测数据的协方差矩阵。Capon算法[1]可以描述为:最小化输出功率,同时保持视线方向的单位增益,其公式如下:
minwwHRxwsubject to wHa(θ)=1.\begin{aligned} & \min _{\mathbf{w}} \quad \mathbf{w}^H \mathbf{R}_{\mathbf{x}} \mathbf{w} \\ & \text { subject to } \quad \mathbf{w}^H \mathbf{a}(\theta)=1 .\end{aligned}wminwHRxw subject to wHa(θ)=1.
我的理解,这里其实类似于波束形成(本质上就是),保持视线方向的单位增益就是波束形成后的最大增益方向。上述公式可使用拉格朗日乘数法求解,其解为:
wLag=Rx−1a(θ)aH(θ)Rx−1a(θ)\mathbf{w}_{L a g}=\frac{\mathbf{R}_{\mathbf{x}}^{-1} \mathbf{a}(\theta)}{\mathbf{a}^H(\theta) \mathbf{R}_{\mathbf{x}}^{-1} \mathbf{a}(\theta)}wLag=aH(θ)Rx−1a(θ)Rx−1a(θ)(4)
将上式代入方程(3),可以得到与方向相关的输出功率,如 :
PCapon (θ)=1aH(θ)Rx−1a(θ)P_{\text {Capon }}(\theta)=\frac{1}{\mathbf{a}^H(\theta) \mathbf{R}_{\mathbf{x}}^{-1} \mathbf{a}(\theta)}PCapon (θ)=aH(θ)Rx−1a(θ)1(5)
经过角度搜索,即可得到Capon算法的测角结果。
2、MUSIC算法原理
MUSIC是多重信号分类的英文缩写(MUltiple SIgnal Classification),信号模型如前所述,一旦我们得到观测数据的协方差矩阵Rx,我们就对其进行特征值分解,并获得信号和噪声分量,如下:
Rx=UsΣsUsH+UnΣnUnH=∑σsususH+∑σnununH\begin{aligned} \mathbf{R}_{\mathbf{x}} & =\mathbf{U}_{\mathbf{s}} \boldsymbol{\Sigma}_{\mathbf{s}} \mathbf{U}_{\mathbf{s}}{ }^H+\mathbf{U}_{\mathbf{n}} \boldsymbol{\Sigma}_{\mathbf{n}} \mathbf{U}_{\mathbf{n}}{ }^H \\ & =\sum \sigma_s \mathbf{u}_{\mathbf{s}} \mathbf{u}_{\mathbf{s}}{ }^H+\sum \sigma_n \mathbf{u}_{\mathbf{n}} \mathbf{u}_{\mathbf{n}}{ }^H\end{aligned}Rx=UsΣsUsH+UnΣnUnH=∑σsususH+∑σnununH(6)
根据信号和噪声子空间之间的正交性[2],我们可以如下形成MUSIC空间谱 :
PMUSIC (θ)=1aH(θ)UnUnHa(θ)P_{\text {MUSIC }}(\theta)=\frac{1}{\mathbf{a}^H(\theta) \mathbf{U}_{\mathbf{n}} \mathbf{U}_{\mathbf{n}}{ }^H \mathbf{a}(\theta)}PMUSIC (θ)=aH(θ)UnUnHa(θ)1(7)
3、算法比较与分析
很容易发现方程式(5)中的 Rx−1R_x^{-1}Rx−1 可以写成:
Rx−1=(UsΣsUsH+UnΣnUnH)−1=UsΣs−1UsH+UnΣn−1UnH=∑1σsususH+∑1σnununH\begin{aligned} \mathbf{R}_{\mathbf{x}}^{-1} & =\left(\mathbf{U}_{\mathbf{s}} \boldsymbol{\Sigma}_{\mathbf{s}} \mathbf{U}_{\mathbf{s}}{ }^H+\mathbf{U}_{\mathbf{n}} \boldsymbol{\Sigma}_{\mathbf{n}} \mathbf{U}_{\mathbf{n}}{ }^H\right)^{-1} \\ & =\mathbf{U}_{\mathbf{s}} \boldsymbol{\Sigma}_{\mathbf{s}}{ }^{-1} \mathbf{U}_{\mathbf{s}}{ }^H+\mathbf{U}_{\mathbf{n}} \boldsymbol{\Sigma}_{\mathbf{n}}{ }^{-1} \mathbf{U}_{\mathbf{n}}{ }^H \\ & =\sum \frac{1}{\sigma_s} \mathbf{u}_{\mathbf{s}} \mathbf{u}_{\mathbf{s}}{ }^H+\sum \frac{1}{\sigma_n} \mathbf{u}_{\mathbf{n}} \mathbf{u}_{\mathbf{n}}{ }^H\end{aligned}Rx−1=(UsΣsUsH+UnΣnUnH)−1=UsΣs−1UsH+UnΣn−1UnH=∑σs1ususH+∑σn1ununH
即等于“信号”项+“噪声”项。当SNR足够大,即σs/σn足够大,则噪声项可以被忽略不计。上述公式(5)可以被近似改写为:
PCapon (θ)≃1aH(θ)UnΣn−1UnHa(θ)P_{\text {Capon }}(\theta) \simeq \frac{1}{\mathbf{a}^H(\theta) \mathbf{U}_{\mathbf{n}} \boldsymbol{\Sigma}_{\mathbf{n}}{ }^{-\mathbf{1}} \mathbf{U}_{\mathbf{n}}{ }^H \mathbf{a}(\theta)}PCapon (θ)≃aH(θ)UnΣn−1UnHa(θ)1
因为求和符号并不改变频谱, 则存在:
PCapon (θ)≃1aH(θ)UnUnHa(θ)=PMUSIC (θ)P_{\text {Capon }}(\theta) \simeq \frac{1}{\mathbf{a}^H(\theta) \mathbf{U}_{\mathbf{n}} \mathbf{U}_{\mathbf{n}}{ }^H \mathbf{a}(\theta)}=P_{\text {MUSIC }}(\theta)PCapon (θ)≃aH(θ)UnUnHa(θ)1=PMUSIC (θ)
即Caopn算法的性能近似等于MUSIC算法的性能,这是由数学上得到证明的。因此,我们得出的结论是:如果SNR足够大,Capon和MUSIC的频谱大致相同,因此它们的性能可能相似。
两种算法在10°和20°的DOA RMSE与SNR的关系:
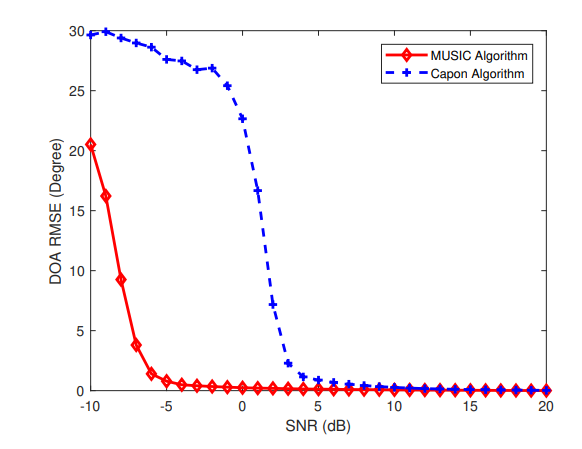
两种算法在SNR=10dB时,Capon和MUSIC算法的目标分离角度与DOA RMSE的关系:
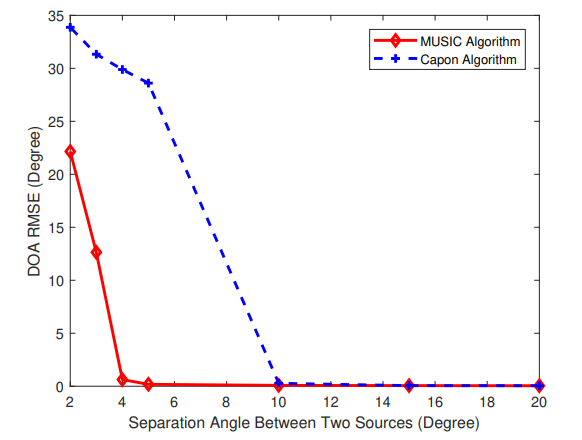
4、MATLAB仿真
设置阵元数为10,阵元间隔为半波长,信源数为3(-10度,0度,20度),快拍数为1024,下图为估计得到的信号谱,低信噪比设置为-8dB,高信噪比设置为10dB。
低信噪比:
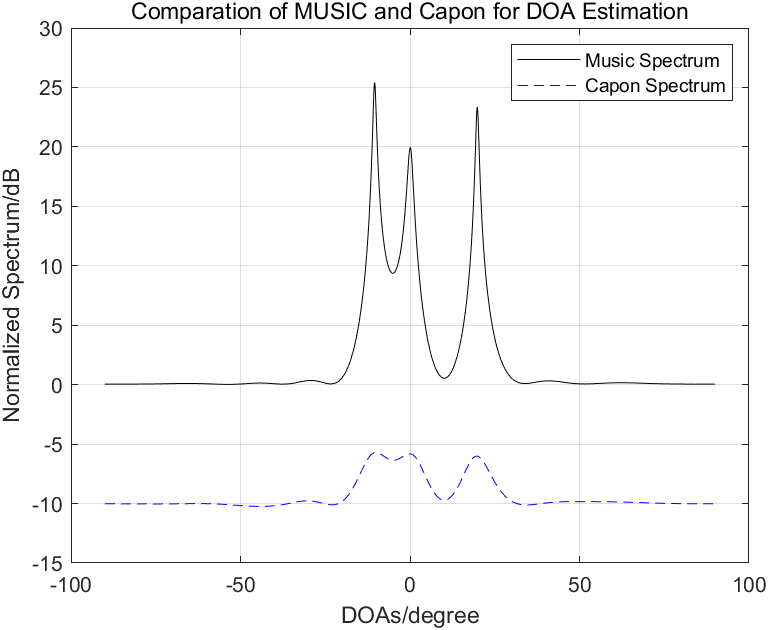
高信噪比:
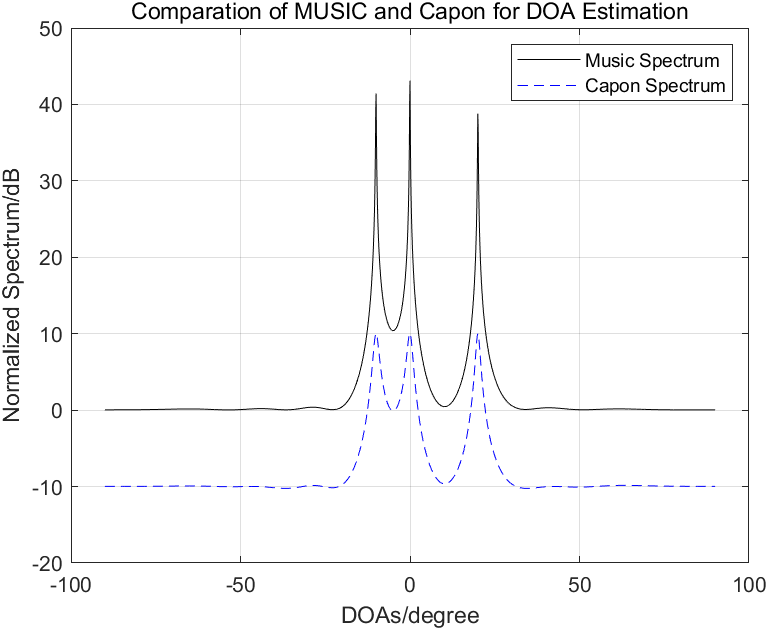
从上图可以看出,在信噪比较低时两种估计算法性能都急剧下降,但是MUSIC算法略优于Capon,而当信噪比较大时,两种算法基本一致。MUSIC谱峰只反映阵列流形矢量与噪声子空间的正交性,与信噪比无关;Capon谱峰是真正的输出功率,与信噪比有关,这就是我前面说Capon其实本质上是波束形成。
仿真代码:
%MUSIC ALOGRITHM
%DOA ESTIMATION BY CLASSICAL_MUSIC
% 运行环境:MATLAB2022b
clear all;
%close all;
clc;
source_number=3;%信元数
sensor_number=10;%阵元数
N_x=1024; %信号长度
snapshot_number=N_x;%快拍数
w=[pi/4 pi/6 pi/3].';%信号频率
l=sum(2*pi*3e8./w)/3;%信号波长
d=0.5*l;%阵元间距
snr=10;%信噪比source_doa=[-10 0 20];%两个信号的入射角度A=[exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(1)*pi/180)/l);exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(2)*pi/180)/l);exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(3)*pi/180)/l)].';%阵列流型s=sqrt(10.^(snr/10))*exp(1j*w*[0:N_x-1]);%仿真信号
%x=awgn(s,snr);
x=A*s+(1/sqrt(2))*(randn(sensor_number,N_x)+1j*randn(sensor_number,N_x));%加了高斯白噪声后的阵列接收信号R=x*x'/snapshot_number;
iR=inv(R);
%[V,D]=eig(R);
%Un=V(:,1:sensor_number-source_number);
%Gn=Un*Un';
[U,S,V]=svd(R);
Un=U(:,source_number+1:sensor_number);
Gn=Un*Un';searching_doa=-90:0.1:90;%线阵的搜索范围为-90~90度for i=1:length(searching_doa)a_theta=exp(-1j*(0:sensor_number-1)'*2*pi*d*sin(pi*searching_doa(i)/180)/l);Pmusic(i)=a_theta'*a_theta./abs((a_theta)'*Gn*a_theta);Pcapon(i)=1./abs((a_theta)'*iR*a_theta);end
plot(searching_doa,10*log10(Pmusic),'k-',searching_doa,10*log10(Pcapon),'b--');
%axis([-90 90 -90 15]);
xlabel('DOAs/degree');
ylabel('Normalized Spectrum/dB');
legend('Music Spectrum','Capon Spectrum');
title('Comparation of MUSIC and Capon for DOA Estimation');
grid on;
5、角度分辨率/精度
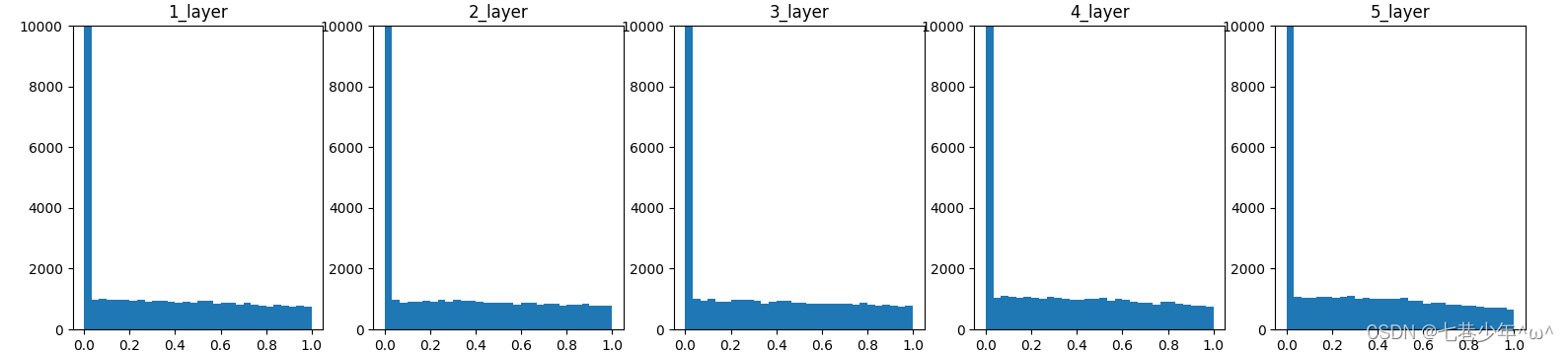
设置阵元数为10,阵元间隔为半波长,信源数为3(-0.5°,0°,0.5°),快拍数为1024,信噪比设置为20dB,下图为估计得到的信号谱,为方便观察进行了归一化。
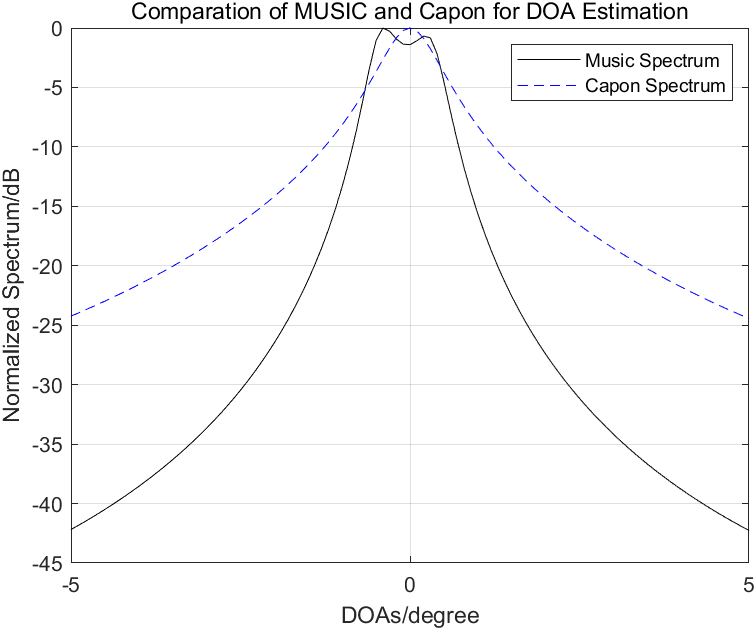
可以看到这种情况下,MUSIC的分辨率是优于Capon法的。具体代码详见https://MLiyPUV6F。
相关文章:

【精选论文 | Capon算法与MUSIC算法性能的比较与分析】
本文编辑:调皮哥的小助理 【正文】 首先说结论: 当信噪比(SNR)足够大时,Capon算法和MUSIC算法的空间谱非常相似,因此在SNR比较大时它们的性能几乎一样,当不同信号源的入射角度比较接近时&…...
卫星、无人机平台的多光谱数据在地质、土壤调查和农业等需要用什么?
近年来,Python编程语言受到越来越多科研人员的喜爱,在多个编程语言排行榜中持续夺冠。同时,伴随着深度学习的快速发展,人工智能技术在各个领域中的应用越来越广泛。机器学习是人工智能的基础,因此,掌握常用…...
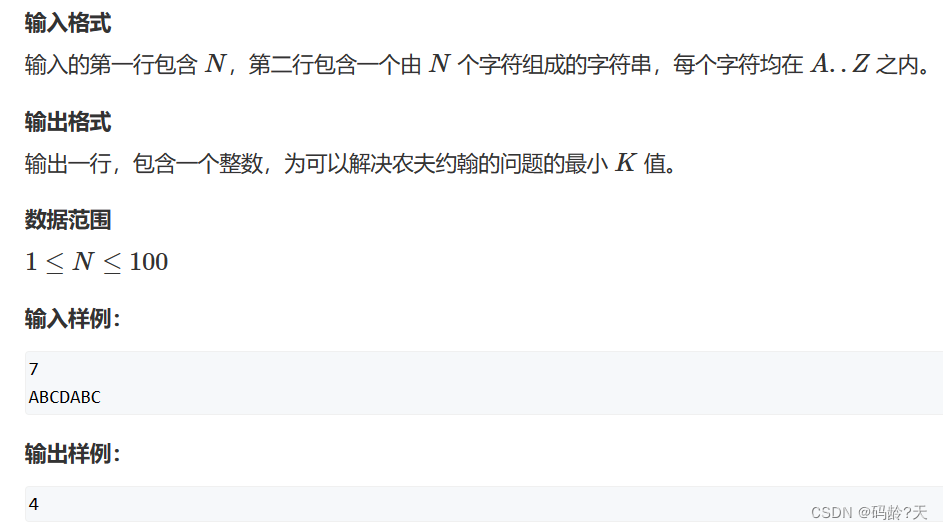
30个题型+代码(冲刺2023蓝桥杯)
愿意的可以跟我一起刷,每个类型做1~5题 ,4月前还可以回来系统复习 2月13日 ~ 3月28日,一共32天 一个月时间,0基础省三 --> 省二;基础好点的,省二 --> 省一 目录 🌼前言 🌼…...
快速且有效减小代码包的方法
前言当我们在发布一些APP或者小程序等比较小的程序时候,常常会对其主包大小进行一定的规定,若超过推荐的主包大小则性能会被大大影响,或者再严重一点就不给你过审。如微信小程序中也对主包有一定的大小要求。对此一些比较复杂的小程序就需要考…...

基于matlab评估星载合成孔径雷达性能
一、前言本示例展示了如何评估星载合成孔径雷达 (SAR) 的性能,并将理论极限与 SAR 系统的可实现要求进行比较。SAR利用雷达天线在目标区域上的运动来提供更精细的方位角分辨率。给定雷达的主要参数(例如工作频率、天线尺寸和带宽&…...

Linux_基本指令
新的专栏Linux入门来啦!欢迎各位大佬补充指正!! Linux_基本指令导入文件绝对路径与相对路径隐藏的文件指令ls查看stat查看文件属性cd进入路径mkdir创建目录touch创建文件rm删除man查询手册cp复制mv移动cat查看文件morelessheadtail时间相关的…...

Keras深度学习实战——使用深度Q学习进行SpaceInvaders游戏
Keras深度学习实战——使用深度Q学习进行SpaceInvaders游戏 0. 前言1. 问题与模型分析2. 使用深度 Q 学习进行 SpaceInvaders 游戏相关链接0. 前言 在《深度Q学习算法详解》一节中,我们使用了深度 Q 学习来进行 Cart-Pole 游戏。在本节中,我们将利用深度Q学习来玩“太空侵略…...
从事架构师岗位快2年了,聊一聊我对架构的一些感受和看法
从事架构师岗位快2年了,聊一聊我和ChatGPT对架构的一些感受和看法 职位不分高低,但求每天都能有新的进步,永远向着更高的目标前进。 文章目录踏上新的征程架构是什么?架构师到底是干什么的?你的终极目标又是什么&#…...

零基础机器学习做游戏辅助第十二课--原神自动钓鱼(二)
一、模拟训练环境 上节课我们已经能够判断人物的钓鱼状态,接下来我们就需要对鱼儿上钩后的那个受力框进行DQN训练。 方案有两个: 使用卷积神经网络直接输入图像对网络进行训练。使用普通网络,自己写代码模拟出图像中三个点的动态并把值给神经网络进行训练。这里我们选用第二…...
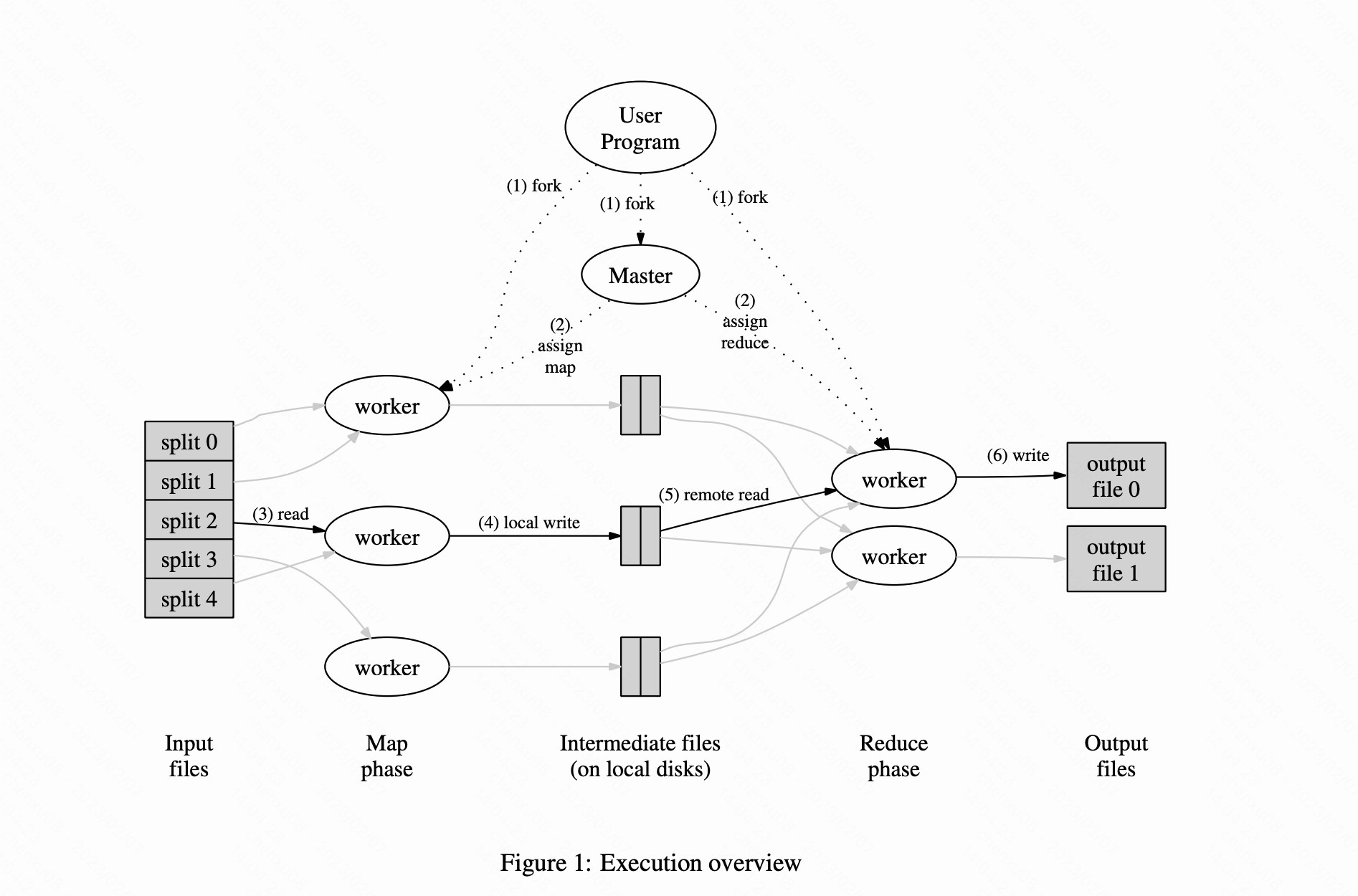
MapReduce paper(2004)-阅读笔记
文章目录前言摘要(Abstract)一、引言( Introduction)二、编程模型(Programming Model)三、实现(Implementation)3.1、执行概述(Execution Overview)3.2、主节点数据结构(Master Data…...
【蒸滴C】C语言指针入门很难?看这一篇就够了
目录 一、前言 二、指针是什么 小结: 三、指针变量是什么 小结: 四、指针在32位机器和64位机器中的差别 32位机器: 64位机器: 小结: 五、指针和指针类型 (1)指针的意义 (2ÿ…...

C++11新的类功能
文章首发公众号:iDoitnow 1. 特殊的成员函数 C11在原有的4个特殊成员函数(默认构造函数、复制构造函数、复制赋值运算符和析构函数)的基础上新增了移动构造函数和移动赋值运算符。这些特殊成员函数在各种情况下是会通过编译器自动提供的。 …...
Laravel创建定时任务
创建一个任务,创建成功后会在App/Console/Commands中生成一个以Test命名的文件,我们可以在这里面写我们的任务指令。 php artisan make:command Test 运行这个定时任务 run 是运行一次,我们可以用来测试是否成功,work是一直运行&a…...

SaveInstanceState
1. 保存与读取当前状态,MainActivity.java public class MainActivity extends AppCompatActivity {private String TAG "MyLog";TextView textView;Button button;Overrideprotected void onCreate(Bundle savedInstanceState) {super.onCreate(savedI…...

Fluent Python 笔记 第 16 章 协程
从句法上看,协程与生成器类似,都是定义体中包含 yield 关键字的函数。可是,在协程中,yield通常出现在表达式的右边(例如,datum yield),可以产出值,也可以不产出——如果 yield 关键字后面没有表…...
山东科技大学校历 代码分析 获得以前学期学年的老版校历
校历-山东科技大学网络安全与信息化办公室http://tech.sdust.edu.cn/wlfw/xl.htm JavaScript var studyStart new Date(2021, 8-1, 30);//8-1 -1没有意义,30代表30号,2021年8月30号开始这个学期 var commonWeeks 19;//这个学期有多少周 var s…...
第五章.与学习相关技巧—权重初始值(随机初始值,Xavier初始值,He初始值)
第五章.与学习相关技巧 5.2 权重初始值 本节将介绍权重初始值的推荐值,并通过实验确认神经网络的学习是否会快速进行。 1.权值衰减 权值衰减就是一种以减少权重参数的值为目的进行学习的方法,通过减少权重参数值来抑制过拟合的情况发生。 2.权重初始值不…...

Linux进程间通信(管道)
进程间通信的目的 数据传输:一个进程需要将它的数据发送给另一个进程 资源共享:多个进程之间共享同样的资源。 通知事件:一个进程需要向另一个或一组进程发送消息,通知它(它们)发生了某种事件(如…...
)
写一个基于node.js的api后台管理系统(三)
创建登录页面 在项目目录下创建一个名为public的文件夹,并在其中创建一个HTML文件login.html。添加以下代码: <!DOCTYPE html> <html> <head><title>Login - Task Management</title> </head> <body><h1…...

【23种设计模式】行为型模式详细介绍(上)
前言 本文为 【23种设计模式】行为型模式 相关内容介绍,下边将对访问者模式,模板模式,策略模式,状态模式,观察者模式,备忘录模式,中介者模式,迭代器模式,解释器模式&…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
