【C语言】编程初学者入门训练(11)
文章目录
- 101. 矩阵相等判定
- 102. 上三角矩阵判定
- 103. 矩阵转置
- 104. 矩阵交换
- 105. 杨辉三角
- 106. 井字棋
- 107. 小乐乐与进制转换
- 108. 小乐乐求和
- 109. 小乐乐定闹钟
- 110. 小乐乐排电梯
101. 矩阵相等判定
-
问题描述:KiKi得到了两个n行m列的矩阵,他想知道两个矩阵是否相等,请你回答他。(当两个矩阵对应数组元素都相等时两个矩阵相等)。
-
输入描述:
- 第一行包含两个整数n和m,表示两个矩阵包含n行m列,用空格分隔。
- 从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
- 从n+2行到2n+1,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第二个矩阵中的元素。
- 1 < n,m < 10
-
输出描述:一行,如果两个矩阵相等输出"Yes"并换行,否则输出"No"并换行。
-
示例:
输入:2 21 23 41 23 4
输出:Yes
- 代码实现:
#include <stdio.h>
int main()
{int n,m,i,j;int arr1[10][10]= {0};int arr2[10][10]= {0};scanf("%d %d",&n,&m);//录入第一个矩阵for(i = 0;i < n;i++){for(j = 0;j < m;j++){scanf("%d",&arr1[i][j]);}}//录入第二个矩阵for(i = 0;i < n;i++){for(j = 0;j < m;j++){scanf("%d",&arr2[i][j]);}}//比较两个数组对应位置的元素for(i = 0;i < n;i++){for(j = 0;j < m;j++){if(arr1[i][j] != arr2[i][j]){printf("No\n");return 0;}}}printf("Yes\n");return 0;
}
102. 上三角矩阵判定
-
问题描述:KiKi想知道一个n阶方矩是否为上三角矩阵,请帮他编程判定。上三角矩阵即主对角线以下的元素都为0的矩阵,主对角线为从矩阵的左上角至右下角的连线。
-
输入描述:第一行包含一个整数n,表示一个方阵包含n行n列,用空格分隔。 (1≤n≤10)从2到n+1行,每行输入n个整数(范围-231~231-1),用空格分隔,共输入n*n个数。
-
输出描述:一行,如果输入方阵是上三角矩阵输出"YES"并换行,否则输出"NO"并换行。
-
示例:
输入:31 2 30 4 50 0 6
输出:YES
- 解题思路:对角线以下的元素都是 0 的,则为上三角矩阵。
- 所有为 0 元素的坐标的特点是:i > j,也就是说只要判断当 i > j 时的所有元素是否为 0 即可。
- 代码实现:
#include <stdio.h>
int main()
{int n,i,j;int arr[10][10];scanf("%d",&n);for(i = 0;i < n;i++){for(j = 0;j < n;j++){scanf("%d",&arr[i][j]);}}for(i = 0;i < n;i++){for(j = 0;j < n;j++){if(i > j){if(0 != arr[i][j]){printf("NO\n");return 0;}}}}printf("YES\n");return 0;
}
103. 矩阵转置
-
问题描述:KiKi有一个矩阵,他想知道转置后的矩阵(将矩阵的行列互换得到的新矩阵称为转置矩阵),请编程帮他解答。
-
输入描述:第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10),从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
-
输出描述:输出m行n列,为矩阵转置后的结果。每个数后面有一个空格。
-
示例:
输入:2 31 2 34 5 6
输出:1 4 2 5 3 6
-
解题思路:原来的列变成行,行则变成列。
-
代码实现:
#include <stdio.h>
int main()
{int n,m,i,j;int arr[10][10];scanf("%d %d",&n,&m);for(i = 0;i < n;i++){for(j = 0;j < m;j++){scanf("%d",&arr[i][j]);}}for(i = 0;i < m;i++){for(j = 0;j < n;j++){printf("%d ",arr[j][i]);//行变成了用j控制,列则由i控制}putchar('\n');} return 0;
}
104. 矩阵交换
- 问题描述:KiKi有一个矩阵,他想知道经过k次行变换或列变换后得到的矩阵。请编程帮他解答。
- 输入描述:
- 第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10)
- 从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
- 接下来一行输入k,表示要执行k次操作(1≤k≤5)。接下来有k行,每行包括一个字符t和两个数a和b,中间用空格格分隔,t代表需要执行的操作,当t为字符’r’时代表进行行变换,当t为字符’c’时代表进行列变换,a和b为需要互换的行或列(1≤a≤b≤n≤10,1≤a≤b≤m≤10)。
- 提示:当t为别的字符时不需要处理
- 输出描述:输出n行m列,为矩阵交换后的结果。每个数后面有一个空格。
- 示例1:
输入:
2 21 23 41r 1 2
输出:3 4 1 2
- 示例2:
输入:2 21 36 82c 1 2t 1 2
- 代码实现:
#include <stdio.h>
int main()
{int n,m,i,j;int arr[10][10];scanf("%d %d",&n,&m);for(i = 0;i < n;i++){for(j = 0;j < m;j++){scanf("%d",&arr[i][j]);}} int k;//操作k次 scanf("%d",&k);//k\n,输入k次之后敲回车还剩个\nchar t;int a,b;for(i = 0;i < k;i++)//每一次操作的过程{scanf(" %c %d %d",&t,&a,&b);//%c前多个空格能消化掉上面剩下的\n//不让t接收到的值变成\nif(t == 'r')//交换a和b行{for(j = 0;j < m;j++){int tmp = arr[a-1][j];arr[a-1][j]= arr[b-1][j];arr[b-1][j]= tmp;}}else if(t == 'c')//交换a和b列{for(j = 0;j < n;j++){int tmp = arr[j][a-1];arr[j][a-1]= arr[j][b-1];arr[j][b-1]= tmp;}} }//交换完之后打印for(i = 0;i < n;i++){for(j = 0;j < m;j++){printf("%d ",arr[i][j]);}putchar('\n');}return 0;
}
105. 杨辉三角
-
问题描述:KiKi知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他解答。杨辉三角,本质上是二项式(a+b)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1, 一个数也为1;每个数等于它左上方和上方的两数之和。
-
输入描述:第一行包含一个整数数n。 (1≤n≤30)
-
输出描述:包含n行,为杨辉三角的前n行,每个数输出域宽为5。
-
示例:
输入:6
输出:11 11 2 11 3 3 11 4 6 4 11 5 10 10 5 1
- 解题思路:
- 前提:每行端点与结尾的数为1。
- 每个数为上方的两数之和,且头两行无需计算全都是1。
- 行列相等的位置的值为1。
- 在框起来的三角形内行都是>=2的,列都是>=1的。当行列都在范围内的时候才需要去计算。
- 代码实现:
#include <stdio.h>
int main()
{int n,i,j;int arr[30][30];scanf("%d",&n);for(i = 0;i < n;i++){for(j = 0;j < n;j++){if(0 == j)//将第0列的值置为1{arr[i][j] = 1;}if(i == j)//将对角线的值置为1{arr[i][j] = 1;}if(i >= 2 && j >= 1){arr[i][j] = arr[i-1][j-1]+ arr[i-1][j];}}}for(i = 0;i < n;i++){//要打印三角形,i打印多少j就打印多少for(j = 0;j <= i;j++){printf("%5d",arr[i][j]);}putchar('\n');}return 0;
}
106. 井字棋
- 问题描述:KiKi 和 BoBo 玩 “井”字棋。也就是在九宫格中,只要任意行、列,或者任意对角线上面出现三个连续相同的棋子,就能获胜。请根据棋盘状态,判断当前输赢。
- 输入描述:三行三列的字符元素,代表棋盘状态,字符元素用空格分开,代表当前棋盘,其中元素为K代表KiKi玩家的棋子,为O表示没有棋子,为B代表BoBo玩家的棋子。
- 输出描述:
- 如果KiKi获胜,输出“KiKi wins!”;
- 如果BoBo获胜,输出“BoBo wins!”;
- 如果没有获胜,输出“No winner!”。
- 示例:
输入:K O BO K BB O K
输出:KiKi wins!
- 解题思路:判断横3、竖3、对角线上的元素是否相等即可。
- 代码实现:
#include <stdio.h>
int main()
{int i,j;char arr[3][3];for(i = 0;i < 3;i++){for(j = 0;j < 3;j++){scanf(" %c",&arr[i][j]);//记得消化掉按下回车之后剩余的\n}}//判断输赢char flag = 'O';for(i = 0;i < 3;i++){//判断某一行的三个是否相等且不为'O'if(arr[i][0]==arr[i][1]&&arr[i][1]==arr[i][2]&&arr[i][1]!='O'){flag = arr[i][1];break;}//判断某一列的三个是否相等且不为'O'if(arr[0][i]==arr[1][i]&&arr[1][i]==arr[2][i]&&arr[1][i]!='O'){flag = arr[1][i];break;}}//判断对角线上的三个是否相等if(arr[0][0]== arr[1][1]&&arr[1][1]==arr[2][2]&&arr[1][1]!='O'){flag = arr[1][1];}//判断另一条对角线if(arr[0][2]== arr[1][1]&&arr[1][1]==arr[2][0]&&arr[1][1]!='O'){flag = arr[1][1];}if('K' == flag) printf("KiKi wins!\n");else if('B' == flag) printf("BoBo wins!\n");else printf("No winner!\n");return 0;
}
107. 小乐乐与进制转换
-
问题描述:小乐乐在课上学习了二进制八进制与十六进制后,对进制转换产生了浓厚的兴趣。因为他的幸运数字是6,所以他想知道一个数表示为六进制后的结果。请你帮助他解决这个问题。
-
输入描述:输入一个正整数n (1 ≤ n ≤ 109)
-
输出描述:输出一行,为正整数n表示为六进制的结果
-
示例1:
- 输入:6
- 输出:10
-
示例2:
- 输入:120
- 输出:320
-
解题思路:
- 先让输入的数 n % 6 得到当前数转换成六进制的最低位;
- 然后让 n / 6,用得到的结果继续 % 6 获得第二低位;
- 不停重复上述步骤,直到 n / 6 的结果为 0 为止。
- 最后将得出的结果翻转过来,就是十进制转六进制的最终结果。
- 代码实现:
#include <stdio.h>
int main()
{int n,i = 0;int arr[40];//将%6,/6后得到的结果存起来scanf("%d",&n);//转换while(n)//如果n不为0,说明还有能拿下来的位{arr[i] = n % 6;i++ ;n = n / 6;//去掉最低位}for(i--;i >= 0;i--){printf("%d",arr[i]);//将得到的数翻转过来就是6进制}return 0;
}
108. 小乐乐求和
-
问题描述:小乐乐最近接触了求和符号Σ,他想计算
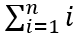
的结果。但是小乐乐很笨,请你帮助他解答。 -
输入描述:输入一个正整数n (1 ≤ n ≤ 109)
-
输出描述:输出一个值,为求和结果。
-
示例1:
- 输入:1
- 输出:1
-
示例2:
- 输入:10
- 输出:55
-
代码实现1:
#include <stdio.h>
int main()
{long long n,sum = 0;scanf("%lld",&n);for(int i = 1;i <= n;i++){sum += i;}printf("%lld\n",sum);return 0;
}
- 代码实现2:
- 等差数列公式:(1 + n) * n / 2
#include <stdio.h>
int main()
{long long n; scanf("%lld",&n);printf("%lld\n",(1+n)*n/2);return 0;
}
109. 小乐乐定闹钟
-
问题描述:小乐乐比较懒惰,他现在想睡觉,然后再去学习。他知道现在的时刻,以及自己要睡的时长,想设定一个闹钟叫他起床学习,但是他太笨了,不知道应该把闹钟设定在哪个时刻,请你帮助他。(只考虑时和分,不考虑日期)
-
输入描述:输入现在的时刻以及要睡的时长k(单位:minute),中间用空格分开。
-
输入格式:hour:minute k(如hour或minute的值为1,输入为1,而不是01),(0 ≤ hour ≤ 23,0 ≤ minute ≤ 59,1 ≤ k ≤ 109)。
-
输出描述:对于每组输入,输出闹钟应该设定的时刻,输出格式为标准时刻表示法(即时和分都是由两位表示,位数不够用前导0补齐)。
-
示例1:
- 输入:0:0 100
- 输出:01:40
-
示例2:
- 输入:1:0 200
- 输出:04:20
-
解题思路:用 k / 60 得到的结果就是对应的小时数,用 k % 60 得到的结果则是对应的分钟数。
-
代码实现:
#include <stdio.h>
int main()
{int h,m,k;scanf("%d:%d %d",&h,&m,&k);h = (h + (m + k) / 60) % 24;//转小时转成24进制m = (m + k) % 60;//将分钟转成60进制printf("%02d:%02d\n",h,m);return 0;
}
110. 小乐乐排电梯
-
问题描述:小乐乐学校教学楼的电梯前排了很多人,他的前面有n个人在等电梯。电梯每次可以乘坐12人,每次上下需要的时间为4分钟(上需要2分钟,下需要2分钟)。请帮助小乐乐计算还需要多少分钟才能乘电梯到达楼上。(假设最初电梯在1层)
-
输入描述:输入包含一个整数n (0 ≤ n ≤ 109)
-
输出描述:输出一个整数,即小乐乐到达楼上需要的时间。
-
示例1:
- 输入:1
- 输出:2
-
示例2:
- 输入:12
- 输出:6
-
代码实现;
#include <stdio.h>
int main()
{int n;scanf("%d",&n);printf("%d\n",(n / 12)*4 + 2);//n / 12得出需要上下几趟电梯,//然后* 4得出轮到乐乐上电梯时的时间,//再加上小乐乐上去的两分钟return 0;
}
相关文章:
【C语言】编程初学者入门训练(11)
文章目录101. 矩阵相等判定102. 上三角矩阵判定103. 矩阵转置104. 矩阵交换105. 杨辉三角106. 井字棋107. 小乐乐与进制转换108. 小乐乐求和109. 小乐乐定闹钟110. 小乐乐排电梯101. 矩阵相等判定 问题描述:KiKi得到了两个n行m列的矩阵,他想知道两个矩阵…...

HTTP 1.1响应码
HTTP 1.1响应码 响应码和信息含义HttpURLConnection1XX信息100 Continue服务器准备接受请求主体,客户端应当发送请求主体;这允许客户端在请求中发送大量数据之前询问服务器是否将接受请求N/A101 Switching Protocols服务器接受客户端在Upgrade首部字段中…...
常用设计模式介绍
java设计模式类型创建型模式:将对象的创建与使用分离结构型模式:如何将类和对象按照某种布局组成更大的格局行为型模式:用于描述类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务23种设计模式介绍1.单例(Singleton&…...

关于货物物品横竖摆放的问题
货车内宽是2.4米。考虑到最多装载,长宽130100的货品,应该横竖摆放。 横竖摆放的数量如何自动计算呢? 采用数学公式,计算如下: 横向摆放数(int)(横长竖高)*数量/4/横长 竖向摆放数数量-横向摆放数 结果如下&#x…...

人员定位需求多,场景目标各不同
GPS技术为现代人带来了许多便利,也提供了诸多基于位置的新型服务。随着科技的发展,人员位置信息在如今的生产生活中也越发重要起来。因此,不同行业领域开始关注人员定位,尤其关注室内人员定位。室内人员定位需求从目的性出发&…...

怎么解决首屏加载速度过慢的问题
怎么解决首屏加载速度过慢的问题首屏加载速度指的是什么?解决方法首屏加载速度指的是什么? 首屏加载速度指的是浏览器从响应用户输入网站地址到首屏内容渲染完成的时间。值得注意的是此时整个网页不一定要全部渲染完成,只需展示当前视窗所需要…...

3d视觉相关论文阅读目录汇总
目录3d视觉综述论文 Deep Learning for 3D Point Clouds: A Survey 基础概念 3d目标检测常见基础概念 3d目标检测 & 自动驾驶 数据集 3d目标检测数据集介绍(数据格式,保存形式,适配算法库等) KITTI数据集 Waymo数据集 nu…...

最简单的计算机视觉
百度为大家提供了计算机视觉模型。能够识别图像中的相关物体。 给大家介绍计算机视觉工具,EasyDL是能够识别物体,图像分类的工具,可以在线,也可以本地下载,本地下载大概1.5G。 图像识别真实距离。 图片真实距离/物体…...

泛微采知连,为组织提供安全、合规、智能的数字化文控系统
作为市场主体,企业需要建立健全的质量管理体系,并且及时更新,以应对激烈的市场竞争,实现企业可持续发展。 质量体系在很大程度上通过文件化的形式表现出来。《质量管理体系要求》(GB/T19001—2016/ISO9001:2015)标准指…...

Python if else对缩进的要求
前面的《Python if else》一节展示了选择结构的三种基本形式,并给出了实例演示,但是大家在编写代码过程中仍然要注意一些细节,尤其是代码块的缩进,这对 if else 选择结构极其重要。 Python 是以缩进来标记代码块的,代…...
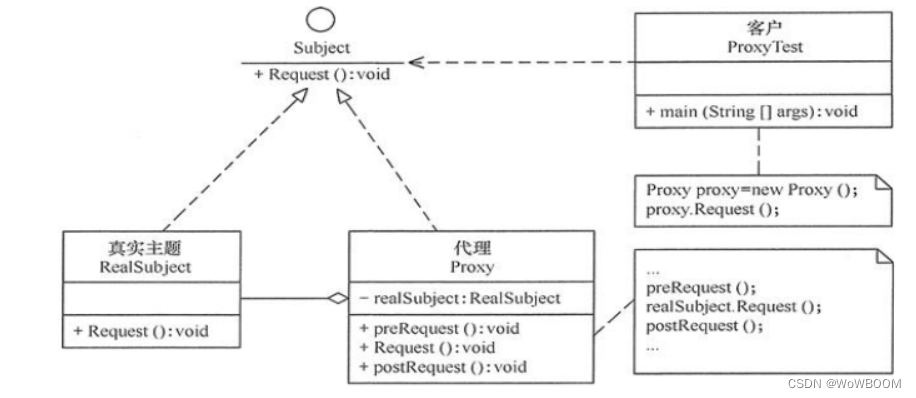
java常用设计模式
java设计模式java设计模式类型常用设计模式单例模式单例模式的两种创建方式饿汉式单例懒汉式单例工厂模式简单工厂模式工厂方法模式抽象工厂模式原型模式代理模式代理模式结构静态代理动态代理jdk代理Cglib代理java设计模式类型 根据完成的工作类型设计模式分为创建型模式、结…...
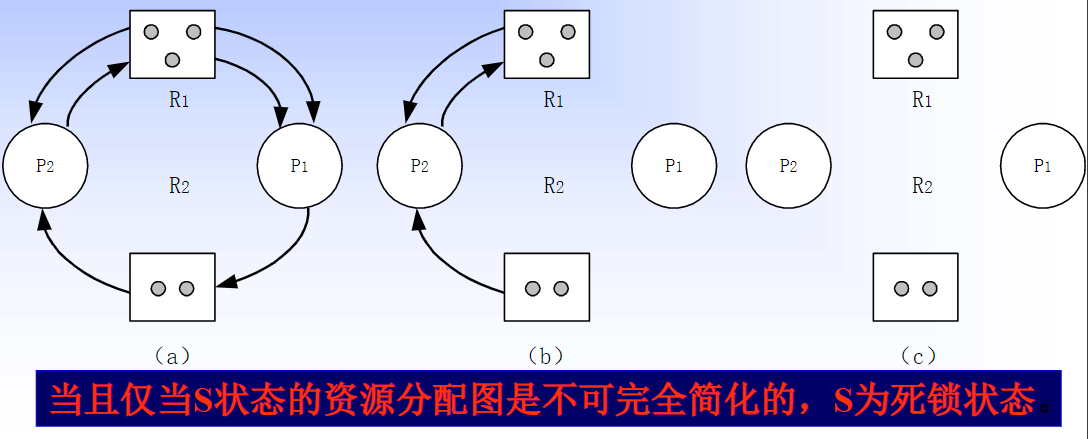
死锁(5.1)
死锁 1 死锁的基本概念 1.1 死锁的定义 死锁是发生在一组相互合作或竞争的线程或进程中的一个问题。因此可以定义为:一组竞争系统资源或相互通信的进程相互的“永久”阻塞。若无外力作用,这组进程将永远不能继续执行。 1.2死锁产生的原因进程 &…...
Python 之 Matplotlib 第一个绘图程序和基本方法
文章目录一、第一个 Matplotlib 绘图程序1. Matplotlib 绘图的基本步骤二、Matplotlib 的基本方法1. 图表名称 plt.title()2. x 轴和 y 轴名称3. 设置 x 轴和 y 轴的刻度4. 显示图表 show()5. 图例 legend()6. 图例的图例位置设置7. 显示每条数据的值 x,y 值的位置一、第一个 M…...
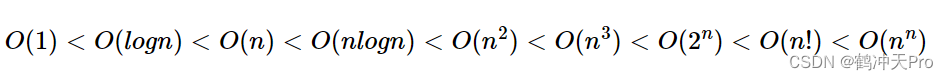
数据结构与算法(一):概述
数据结构学了有一年左右的时间了,但是一直没有详细地总结一下,现在回想起来,感觉有些内容忘记了。所以接下来一段时间我将重新归纳总结一下,算是温故而知新了。 一、数据结构 1、定义 数据结构是计算机存储、组织数据的方式。在…...

Spring3之Bean的属性详解
简介 Spring 中大量使用到 Bean 的注入来实现各个模块之间的依赖,本章将详细介绍 Bean 的主要属性 id 和 name 属性 每个 Bean 可以有一个 id 属性,并可以根据该 id 在 IoC 容器中查找该 Bean,该 id 属性值必须在IoC 容器中唯一 可以不指定…...
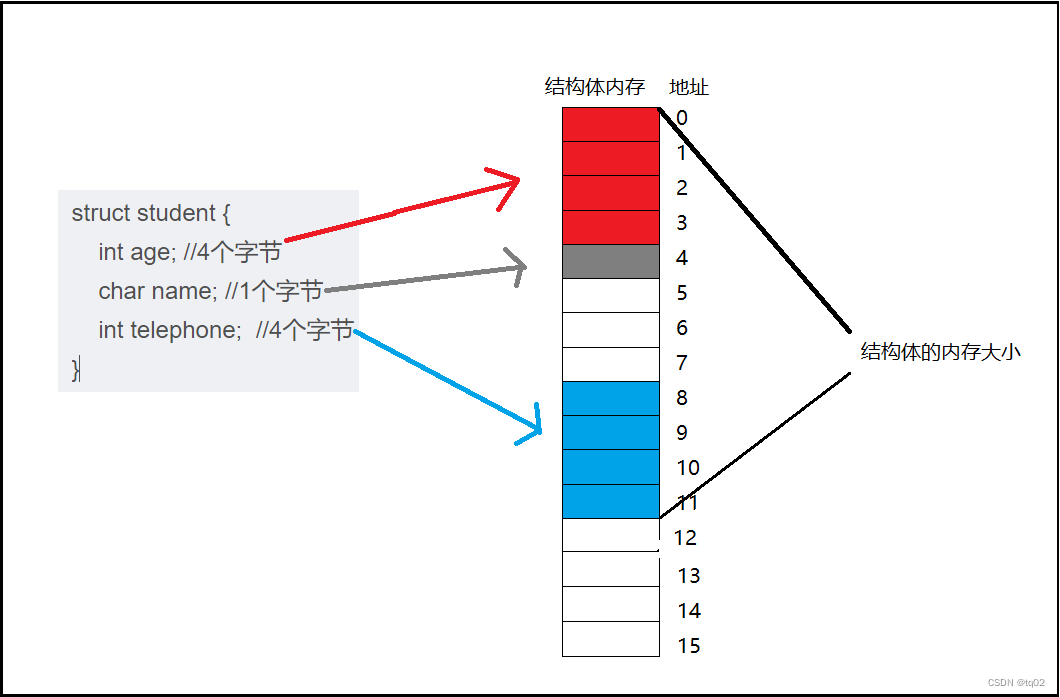
C语言之结构体内存的计算
结构体的内存 一.提出疑问 结构体占用的是一片连续的内存空间,大小是由成员变量的类型决定的。但并不是计算所有成员变量的类型大小之和那么简单。 先举一个实例: struct student {int age; //4个字节int telephone; //4个字节 }; int main() {struc…...
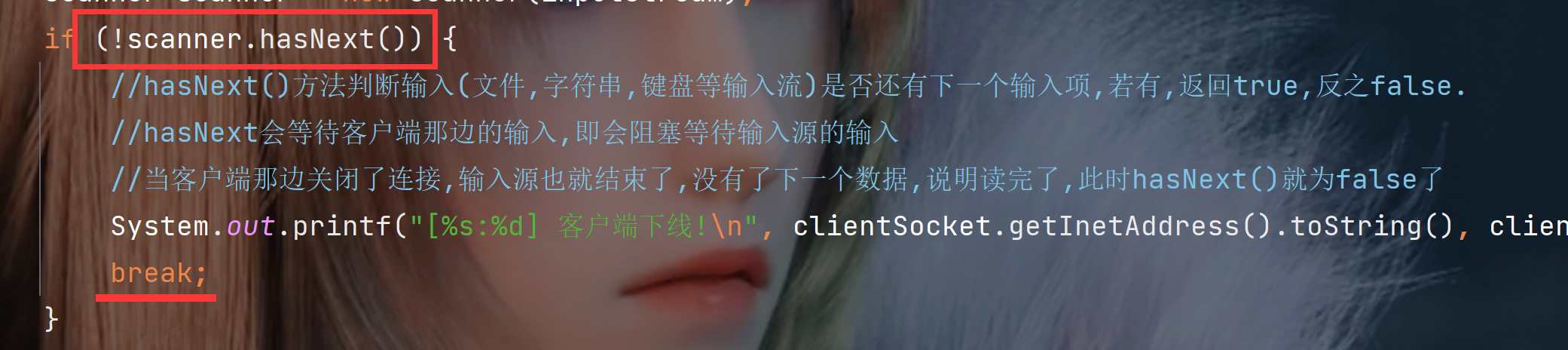
Java网络编程之UDP和TCP套接字
文章目录一. 网络编程概述二. UDP网络编程1. UDP套接字2. UDP客户端回显服务器程序2.1 UDP回显服务器2.2 UDP客户端2.3 UDP实现查词典的服务器三. TCP网络编程1. TCP套接字2. TCP客户端回显服务器程序2.1 TCP回显服务器2.2 TCP客户端2.3 解决服务器无法同时出力多个客户端的问题…...
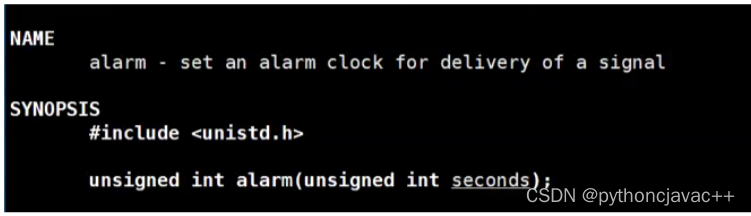
Linux进程信号产生以及捕捉
一.什么是信号 生活中,有哪些信号相关的场景呢,比如:红绿灯,闹钟,转向灯等等 1.这里我们要知道,你为什么认识这些信号呢,记住了对应场景下的信号+后续是有”动作“要你执行的 2.我们…...
常用知识点汇总)
11. GLSL(OpenGL Shader Language)常用知识点汇总
1. 说明: 在使用OPenGL进行三维模型渲染时,需要使用到两个着色器对模型进行位置设置和颜色设置,分别为顶点着色器和片段着色器,这两个着色器是使用 GLSL 语法进行编写的。这篇文章总结了一些GLSL中的一些基本语法知识。 2. 基本…...

转发一张网络工程师考试的试卷2021.5.15
网络工程师考试 单选题 (30题,每题1分,共30分) 1. 你在一个网络中实现DHCP服务,配置一些计算机成为DHCP客户端,由于工作需要,一台系统为Windows 10 的客户端要把从DHCP服务器获得的地址释放&a…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...



