python3.9安装和pandas安装踩坑处理
0、先决条件:系统内最好先安装有gcc、libffi-devel等
1、安装包下载
https://www.python.org/downloads/source/
2、解压安装包并上传到/usr/local/python3.9
3、打开shell
cd /usr/local/python3.9
要先把python3.9的所有文件复制到/usr/local/python3.9才会成功
./configure --prefix=/usr/local/python3.9
报权限不足时,用下面这个
bash ./configure --prefix=/usr/local/python3.9
4、make并安装
make &&make install
报错:configure: error: no acceptable C compiler found in $PATH 说明没gcc或版本过低
http://ftp.gnu.org/gnu/gcc/
下载新的gcc安装好后再重新make,make的过程中出现GB2132时,说明是系统语言现在是中文,需要切换为英文
localectl set-locale LANG=en_US.UTF-8source /etc/locale.conf
5、当make成功后,添加环境变量:
vi /etc/profile
#在最后添加
PATH=/usr/local/python3/bin:$PATH
#保存后,刷新配置文件
source /etc/profile
6、添加软连接
ln -s /usr/local/python3.9/bin/pip3 /usr/bin/pip3
ln -s /usr/local/python3.9/bin/python3 /usr/bin/python3
当报该路径已存在其他版本的python时,可先进行备份
mv /usr/bin/python3 /usr/bin/python3_back
7、 检验python3 是否安装成功
python3
8、安装第三方框架
pypi.org 下载包
whl类型的文件
pip3 install numpy-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
tar.gz类型安装
tar -zvxf pyspark-3.3.1.tar.gz
cd /opt/python3/pyspark-3.3.1
python3 setup.py install
安装pandas是最麻烦的,报错“ModuleNotFoundError: No module named ‘_ctypes’”模块缺失处理办法是以下:
http://mirror.centos.org/centos/7/os/x86_64/Packages/libffi-devel-3.0.13-19.el7.x86_64.rpm
rpm -ivh libffi-devel-3.0.13-19.el7.x86_64.rpm
bash ./configure --prefix=/usr/local/python3
make &&make install
当已经装好pandas后,运行import pandas 出现 ModuleNotFoundError: No module named ‘_bz2’
处理办法是
把_bz2.cpython-39-x86_64-linux-gnu.so 放到/usr/local/python3.9/lib/python3.9/lib-deload下
记得是把36m改成39
下载地址:https://pan.baidu.com/s/1GzUY4E0G2yVUfqxHOIzn1A
提取码:oiwh
相关文章:

python3.9安装和pandas安装踩坑处理
0、先决条件:系统内最好先安装有gcc、libffi-devel等 1、安装包下载 https://www.python.org/downloads/source/ 2、解压安装包并上传到/usr/local/python3.9 3、打开shell cd /usr/local/python3.9要先把python3.9的所有文件复制到/usr/local/python3.9才会成功…...
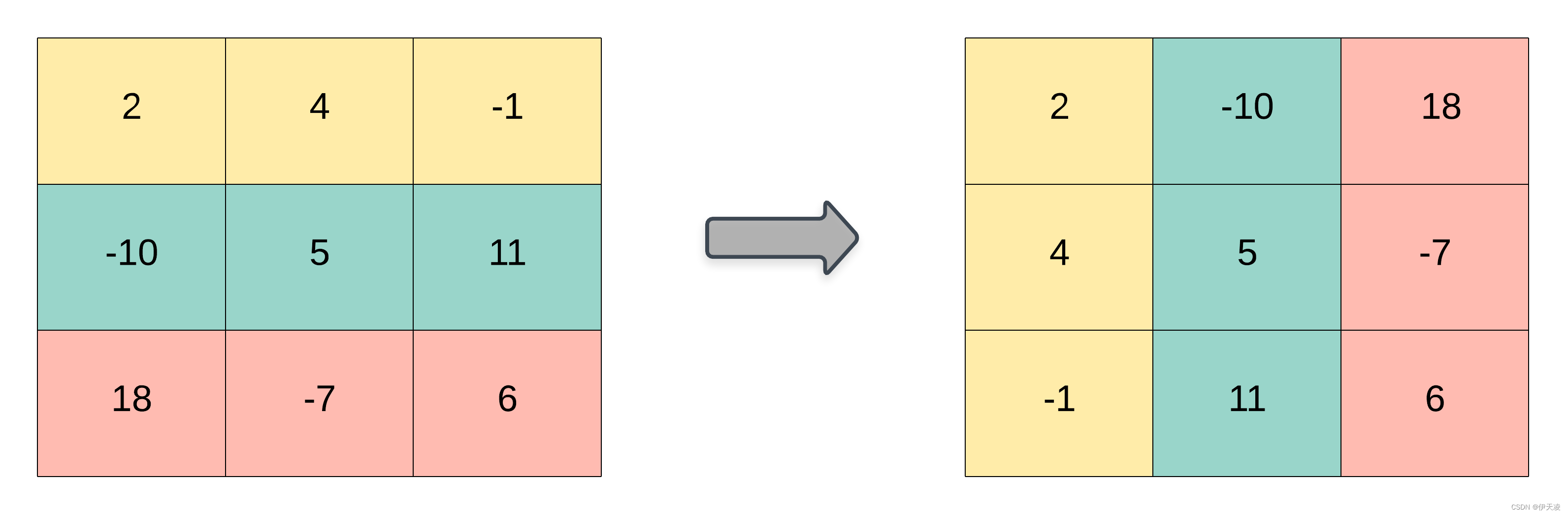
2023.2.15每日一题——867. 转置矩阵
每日一题题目描述解题核心解法一:二维表示 模拟解法二:一维表示 模拟题目描述 题目链接:867. 转置矩阵 给你一个二维整数数组 matrix, 返回 matrix 的 转置矩阵 。 矩阵的 转置 是指将矩阵的主对角线翻转,交换矩阵…...
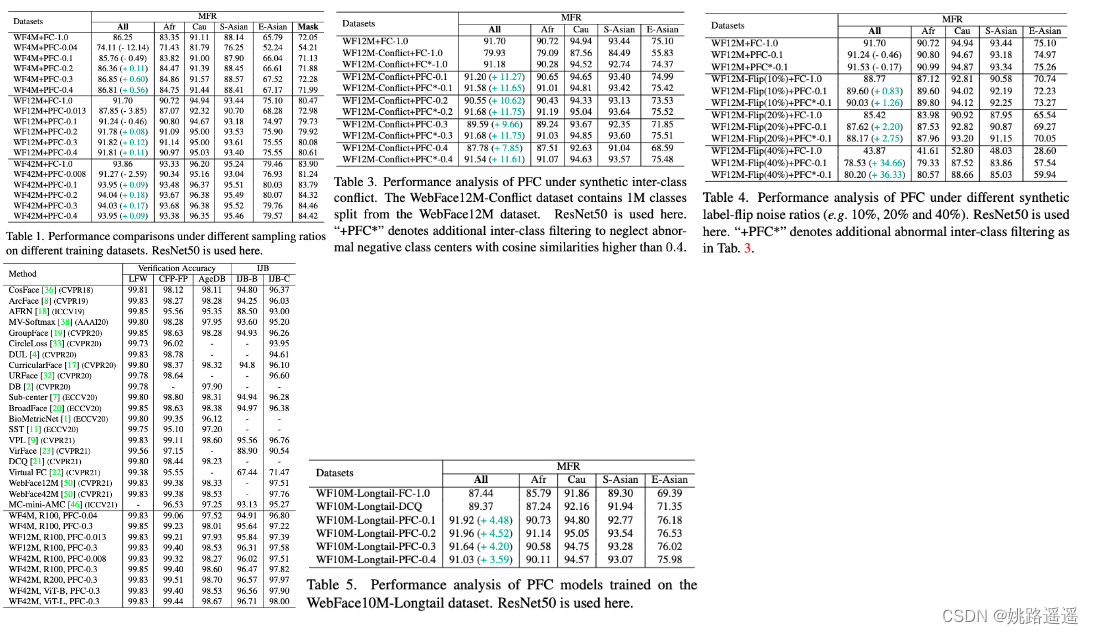
【人脸识别】Partial-FC:让你在一台机器上训练1000万个id人脸数据集成为可能!
论文题目:”Killing Two Birds with One Stone: Efficient and Robust Training of Face Recognition CNNs by Partial FC“ -CVPR 2022 代码地址:https://arxiv.org/pdf/2203.15565.pdf 代码地址:https://github.com/deepinsight/insightfac…...

递归方法读取任意深度的 JSON 对象的键值
有以下json字符串 {"name":"John","age":30,"address":{"city":"New York","state":"NY","zip":"10001","coordinates":{"latitude":40.712776,&q…...
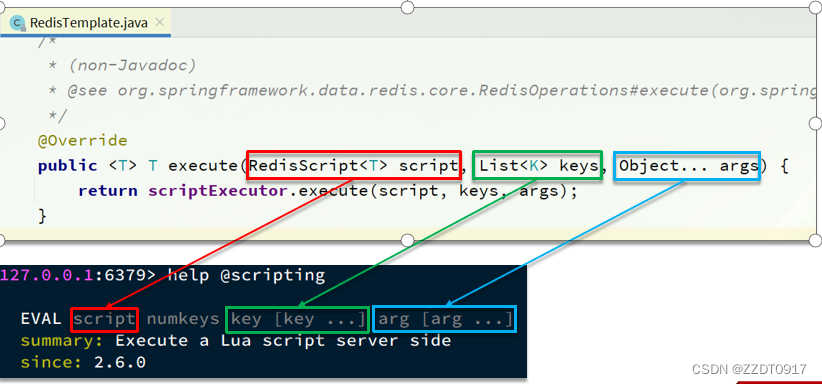
黑马redis学习记录:分布式锁
一、基本原理和实现方式对比 分布式锁:满足分布式系统或集群模式下多进程可见并且互斥的锁。 分布式锁的核心思想就是让大家都使用同一把锁,只要大家使用的是同一把锁,那么我们就能锁住线程,不让线程进行,让程序串行…...

对React-Fiber的理解,它解决了什么问题?
对React-Fiber的理解,它解决了什么问题?Fiber用来解决什么问题?Fiber是什么?Fiber是如何解决问题的?Fiber用来解决什么问题? JavaScript引擎和页面渲染引擎两个线程是互斥的,当其中一个线程执行…...
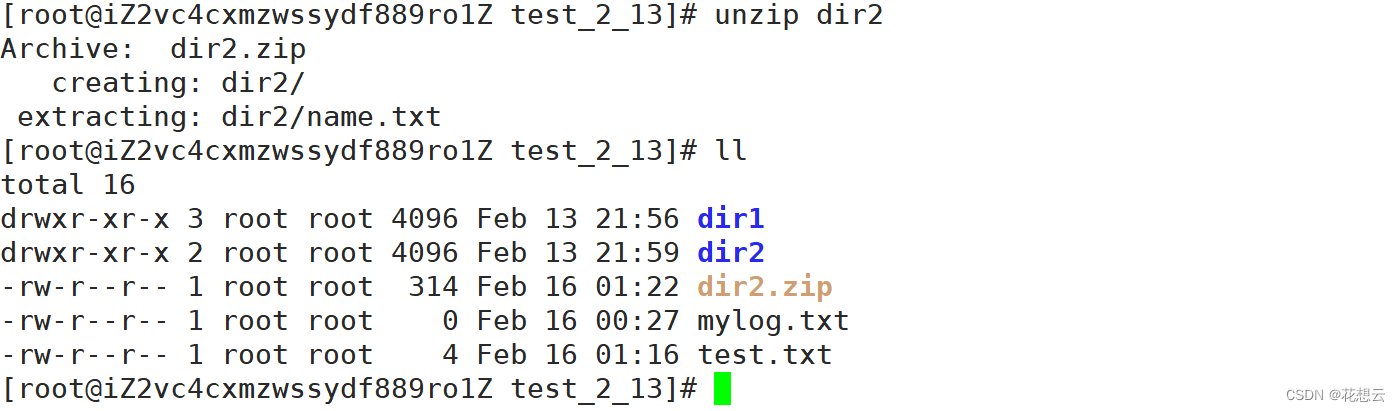
【Linux】初学Linux你需要掌握这些基本指令(二)
目录 1.man指令 2.cp指令 3.mv指令 4.tree指令 5.echo指令 6.more指令 7.less指令(重要) 8.head与tail指令 9.date指令 显示时间常用参数: 设置时间常用参数: 10.cal指令 11.find & whereis & which指令 …...
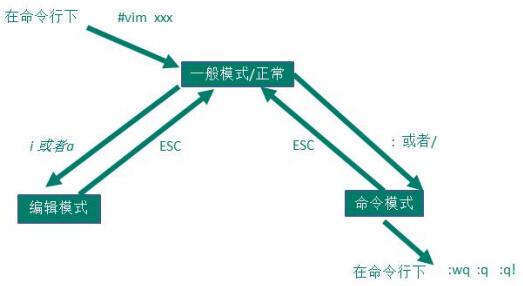
Linux中VI/VIM 编辑器
1、概述所有Linux系统都会内置vi文本编辑器vim是vi的升级版,可以主动以字体颜色分辨语法的正确性,代码补完和编译,错误跳转等功能。2、vi和vim的三种模式基本上 vi/vim 共分为三种模式,分别是一般模式、编辑模式、命令模式2.1、一…...
PDF怎么转换成Word?两种PDF免费转Word方法推荐
不知道你们有没有发现,我们在网上下载的很多资料都是PDF格式的,尽管PDF文件也可以通过专门的PDF编辑器来编辑,但是PDF文档作为版式文档,编辑起来还是存在很多局限性,所有当我们需要大量编辑修改文档的时候,…...
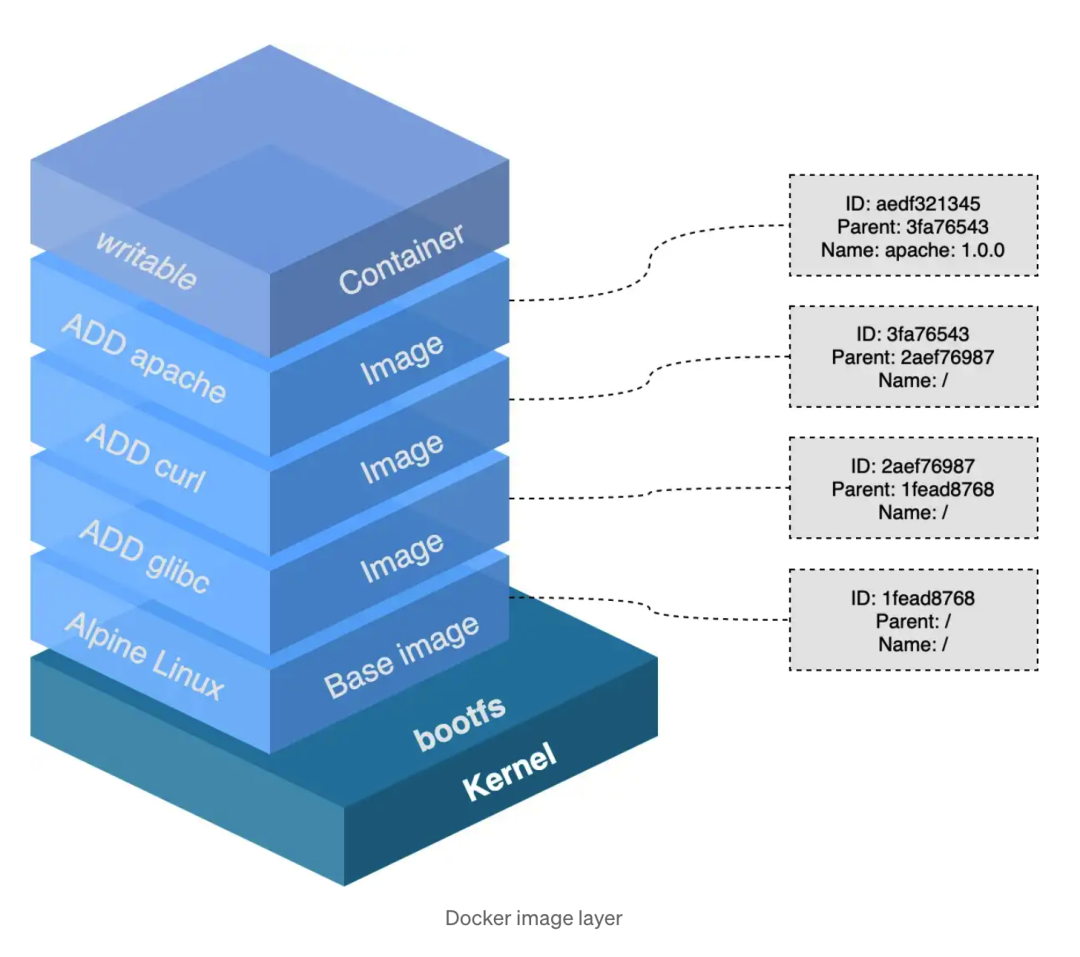
极兔一面:Dockerfile如何优化?注意:千万不要只说减少层数
说在前面 在40岁老架构师 尼恩的读者交流群(50)中,面试题是一个非常、非常高频的交流话题。 最近,有小伙伴面试极兔时,遇到一个面试题: 如果优化 Dockerfile? 小伙伴没有回答好,只是提到了减少镜像层数。…...
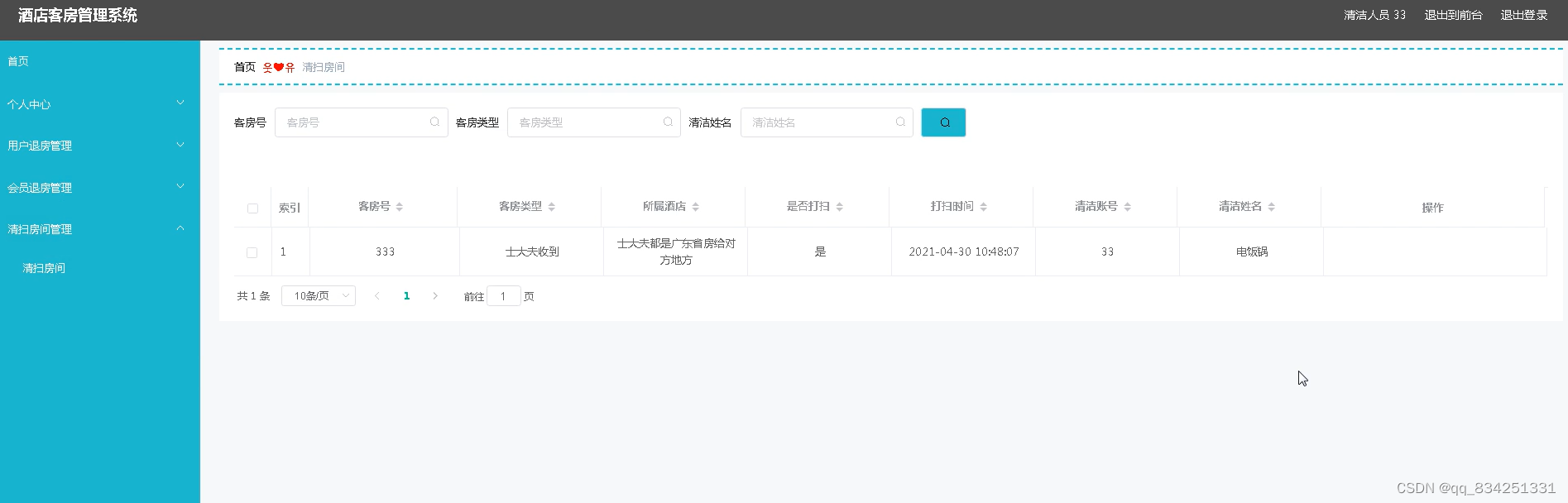
SpringBoot+Vue实现酒店客房管理系统
文末获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏…...
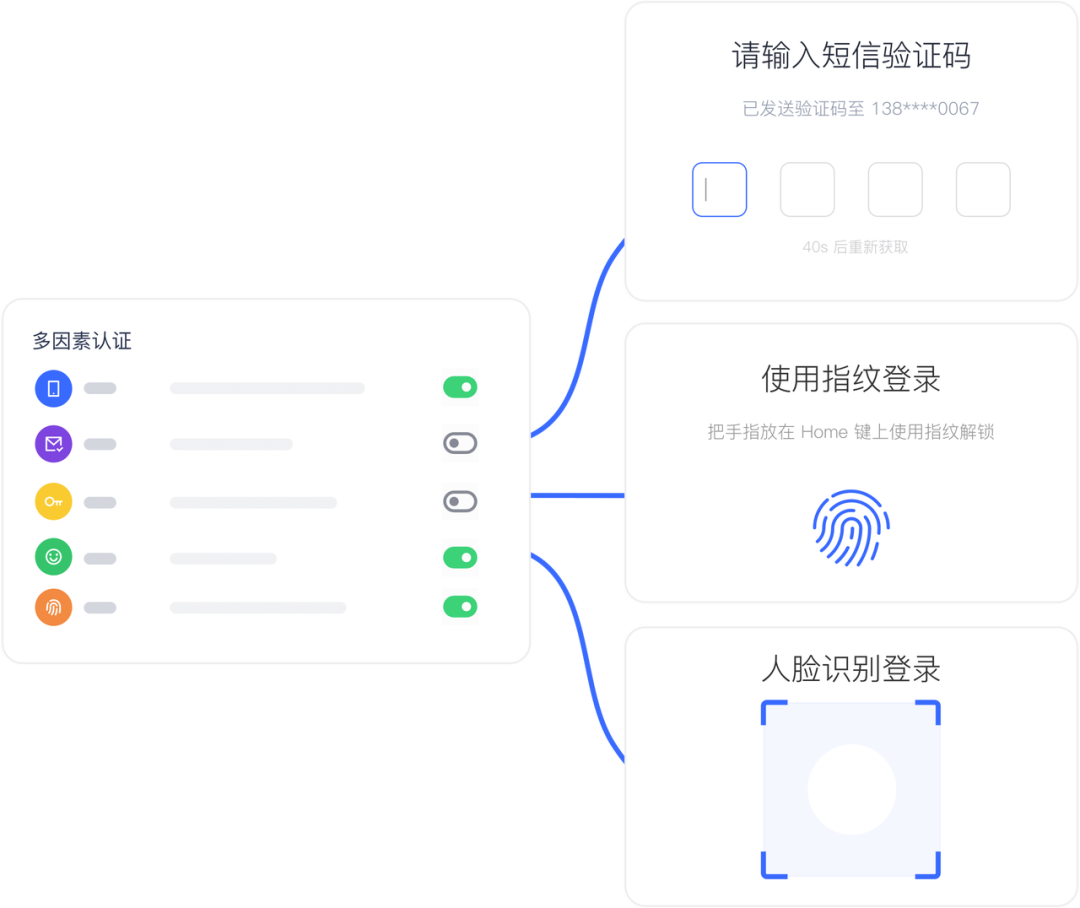
自适应多因素认证:构建不可破解的企业安全防线|身份云研究院
打开本文意味着你理解信息安全的重要性,并且希望获取行业最佳实践来保护你所在组织的信息安全。本文将带你了解多因素认证(MFA:Multi-Factor-Authentication)对于企业信息安全的重要性以及实施方法。 多因素认证(MFA&…...

阶段二8_集合ArrayList_学生管理系统_详细步骤
一.学生管理系统案例 1.需求: 针对目前我们的所学内容,完成一个综合案例:学生管理系统! 该系统主要功能如下: 1.添加学生:通过键盘录入学生信息,添加到集合中 2.删除学生:通过键盘录…...

一篇解决Linux 中的负载高低和 CPU 开销并不完全对应
负载是查看 Linux 服务器运行状态时很常用的一个性能指标。在观察线上服务器运行状况的时候,我们也是经常把负载找出来看一看。在线上请求压力过大的时候,经常是也伴随着负载的飙高。 但是负载的原理你真的理解了吗?我来列举几个问题&#x…...
关于IDM下载器,提示:一个假冒的序列号被用来注册……idea项目文件路径报红
关于IDM下载器,提示:一个假冒的序列号被用来注册……到C:\Windows\System32\drivers\etc 修改目录下面的hosts文件(如果没有修改的权限就右键属性hosts文件修改user的权限为完全控制),在hosts里面增加以下内容…...
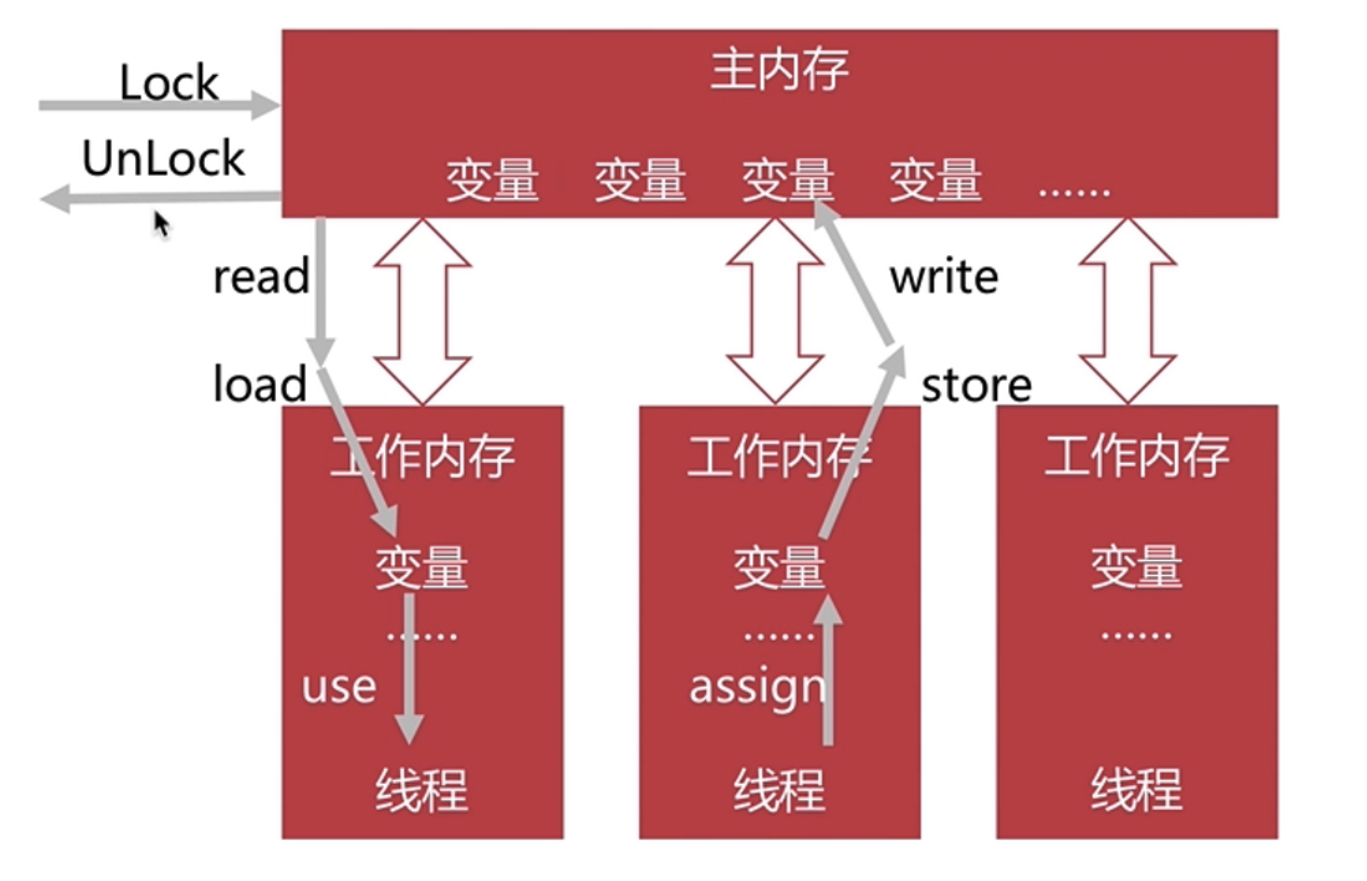
JVM - 高效并发
目录 Java内存模型和内存间的交互操作 Java内存模型 内存间的交互操作 内存间交互操作的规则 volatile特性 多线程中的可见性 volatile 指令重排原理和规则 指令重排 指令重排的基本规则 多线程中的有序性 线程安全处理 锁优化 锁优化之自旋锁与自适应自旋 锁优…...

中小学智慧校园电子班牌系统源码 Saas云平台模式
智慧电子班牌区别于传统电子班牌,智慧校园电子班牌系统更加注重老师和学生的沟通交流和及时数据交互。学校为每个教室配置一台智能电子班牌,一般安装于教室门口,用来实时显示学校通知、班级通知,可设置集中分布式管理,…...

记录一次服务器被攻击的经历
突然收到阿里云发过来的异常登陆的信息: 于是,急忙打开电脑查看对应的ECS服务器的记录: 发现服务器的cpu占用率异常飙升,所以可以大概断定服务器已经被非法入侵了。 通过自己的账号登陆后,发现sshd服务有异常的链接存…...
Python解题 - CSDN周赛第29期 - 争抢糖豆
本期问哥是志在必得,这本算法书我已经觊觎许久,而之前两次因为种种原因未能如愿。因此,问哥这几天花了不少时间,把所有之前在每日一练做过的题目重新梳理了一遍。苦心人,天不负,感谢官方大大! 第…...

C代码中访问链接脚本中的符号
一、目的在之前的《GNU LD脚本命令语言(一)》、《GNU LD脚本命令语言(二)》我们介绍了GNU链接脚本的知识点,基本上对链接脚本中的SECTION、REGION、以及加载地址与执行地址的关系等内容有了一定的了解。本篇主要讲解链…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
