Python解题 - CSDN周赛第29期 - 争抢糖豆
本期问哥是志在必得,这本算法书我已经觊觎许久,而之前两次因为种种原因未能如愿。因此,问哥这几天花了不少时间,把所有之前在每日一练做过的题目重新梳理了一遍。苦心人,天不负,感谢官方大大!
第一题:订班服
小A班级订班服了! 可是小A是个小糊涂鬼,整错了好多人的衣服的大小。 小A只能自己掏钱包来补钱了。 小A想知道自己至少需要买多少件衣服。
输入描述:第一行输入一个整数n。(1<=n<=100)表示衣服的数量。 以下n行输入n个尺码。表示订单中衣服的尺码。 接下来n行输入n个尺码。小A订的衣服尺码。 尺码表:M,S,L,XL,XLL,XLLL,XLLLL,XLLLLL。
输出描述:输出至少需要买多少件衣服。
示例:
示例 输入 2
XL
X
M
X输出 1
分析
简单题。需要 n 件衣服,买了 n 件衣服,所以只要把需要的 n 件衣服每种尺码的个数,减去已购买的衣服相应尺码的个数,如果大于0就说明该尺码还需要购买。所以最直接的办法就是用哈希表记录每种尺码的个数,然后再逐个检查。
Python已经提供了内置Counter类,可以自动生成字典,而且支持加减法,连逐个检查这一步都省去了:直接相减,剩下的数字加在一起就是答案。
参考代码
n = int(input().strip())
arr1 = [input().strip() for _ in range(n)]
arr2 = [input().strip() for _ in range(n)]
from collections import Counter
clothes = Counter(arr1) - Counter(arr2)
print(sum(clothes.values()))第二题:争抢糖豆
抓糖豆,小Q与小K都喜欢吃糖豆。 但是糖豆分两种,超甜糖豆和普通糖豆。 现在有w个超甜糖豆和b个普通糖豆。 小Q和小K开始吃糖豆,他们决定谁先吃到超甜糖豆谁就获胜。 小K每次吃的时候会捏碎一颗糖豆。 小Q先吃,小Q想知道自己获胜的概率。 如果两个人都吃不到超甜糖豆小K获胜。
输入描述:输入两个整数w,b。(0<=w,b<=1000)
输出描述:答案保留9位小数。
示例:
示例 输入 1 3 输出 0.500000000
分析
也是以前考过的老题了。可以用递归或动态规划来做,但本题的状态转移不太容易一眼发现,所以可能不少人会觉得难。因为问到概率(胜率),所以本质上还是需要用数学来表达。
以动态规划为例(递归容易超时),我们用 表示当有
颗超甜糖豆,和
颗普通糖豆时自己的胜率。因为先吃到超甜糖豆就获胜了,所以自己要想获胜,只能分成两种情况:
- 先吃到超甜糖豆,概率是
,此情况下直接获胜;
- 先吃到普通糖豆,但是对手也吃到普通糖豆,所以游戏继续,自己还有获胜的可能。(这里有一个特判的情况:如果只有一颗普通糖豆,而自己先吃到普通糖豆的话,无论如何也是输,后面自然就不用算了。)因此,自己和对手都吃到普通糖豆的概率是
。(如果一时看不懂可以多琢磨几遍,乘号左边是自己吃到普通糖豆的概率,右边是自己吃完后对方也吃到普通糖豆的概率,看懂了再继续。)
如果没有“捏碎糖豆”的操作,分析到这就结束了,状态转移就是把这两种情况的胜率加在一起,方程如下:
(因为自己和对手总共吃了两颗普通糖豆,所以上面第二种情况的概率还要乘以 才是胜率。)
如果上面的内容理解了,我们再来分析“捏碎糖豆”的情况。
捏碎糖豆也有两种情况:
- 捏碎了普通糖豆。影响不大,但是上面的第二种状态要接着乘上捏碎普通糖豆的概率,再乘以
。合在一起的胜率就是
。
- 捏碎了超甜糖豆。则二人虽不分胜负,理论上自己还存在胜利的可能(如果还剩下超甜糖豆的话),但是同样地,状态转移方程变了,胜率变成了:
。
这两种捏碎糖豆的情况属于同一决策层级,可以加在一起。于是把捏碎糖豆考虑进来,得到最终的状态转移方程如下:
此外,如之前所述,还要考虑几个特判的情况:
- 没有超甜糖豆,胜率为0,不用计算。
- 没有普通糖豆,胜率100%。
- 只有一颗普通糖豆,胜率为
,因为如果自己先吃到普通糖豆,必输。
很显然,上面第二、三可以合并,而第一条可以在初始化的时候把 的时候设置为0。代码如下:
参考代码
w, b = map(int, input().split())
dp = [[0]*(b+1) for _ in range(w+1)]
for i in range(1, w+1):for j in range(b+1):if j <= 1:dp[i][j]=i/(i+j)else:dp[i][j]=i/(i+j)+j/(i+j)*(j-1)/(i+j-1)*((j-2)/(i+j-2)*dp[i][j-3]+i/(i+j-2)*dp[i-1][j-2])
print(f"{dp[w][b]:.9f}")输出结果的时候要注意,题目要求必须保留9位小数,空位用0补全,所以要设置占位符。
第三题:走楼梯
现在有一截楼梯,根据你的腿长,你一次能走 1 级或 2 级楼梯,已知你要走 n 级楼梯才能走到你的目的楼层,请实现一个方法,计算你走到目的楼层的方案数。
输入描述:输入整数n。(1<=n<=50)
输出描述:输出方案数。
示例:
示例 输入 5 输出 8
分析
很明显,答案是斐波那契数列。因为一次只能走 1 级或 2 级楼梯,所以第 n 级阶梯可以由 n-1 级阶梯走过来,也可以由 n-2 级阶梯走过来。如果用函数 表示走上第 n 级阶梯的方案数,可得
因为本题 n 范围较小(1<=n<=50),所以使用递归来做应该也没问题。不过更常用的做法是递推,也算是斐波那契的模板题了。
参考代码
n = int(input().strip())
a = b = 1
for _ in range(n):a, b = b, a+b
print(a)第四题:打家劫舍
一个小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额的非负整数数组,计算不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
输入描述:输入一个正整数n代表房屋的数量(n≤100),接着输入n个非负整数代表每间房屋的现金数量
输出描述:小偷能偷取的最大金额。
示例:
示例 输入 4
1 2 3 1输出 4
分析
力扣原题,经典的打家劫舍系列,但凡刷过点题的相信都做过。而且这里选取的是该系列最简单的一道,动态规划入门题,相关题解太多了,这里问哥只简单说两句吧。
因为相邻的房屋不能同时被盗,所以小偷在当前房屋只有两种选择:不偷当前房屋——继承上个房屋可偷取的的最大金额,偷当前房屋——上上个房屋可偷取的最大金额(因为上个房屋不能偷)加上当前房屋的金额,而当前房屋可偷取的最大金额就等于这两种选择中较大的金额。
如果用 代表当前房屋可偷取的最大金额,
表示当前房屋的金额,可用公式表示如下:
类似斐波那契数列,可以看出 仅由
和
得到(
是给定数组),所以可以使用滚动数组优化空间,换句话说就是只需要额外两个变量循环保存
和
的值即可。
参考代码
n = int(input().strip())
arr = [int(item) for item in input().strip().split()]
a = b = 0
for i in arr:a, b = b, max(b, a+i)
print(b)相关文章:
Python解题 - CSDN周赛第29期 - 争抢糖豆
本期问哥是志在必得,这本算法书我已经觊觎许久,而之前两次因为种种原因未能如愿。因此,问哥这几天花了不少时间,把所有之前在每日一练做过的题目重新梳理了一遍。苦心人,天不负,感谢官方大大! 第…...

C代码中访问链接脚本中的符号
一、目的在之前的《GNU LD脚本命令语言(一)》、《GNU LD脚本命令语言(二)》我们介绍了GNU链接脚本的知识点,基本上对链接脚本中的SECTION、REGION、以及加载地址与执行地址的关系等内容有了一定的了解。本篇主要讲解链…...
MySQL 8:MySQL索引
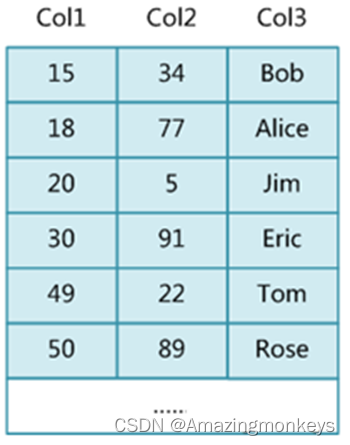
索引就是通过一定的算法建立数据模型,用于快速查找某一列中具有特定值的行。如果没有索引,MySQL 必须从第一条记录开始读取整个表,直到找到相关的表。表越大,查询数据所花费的时间就越多。如果表中查询的列有索引,MySQ…...
JVM详解
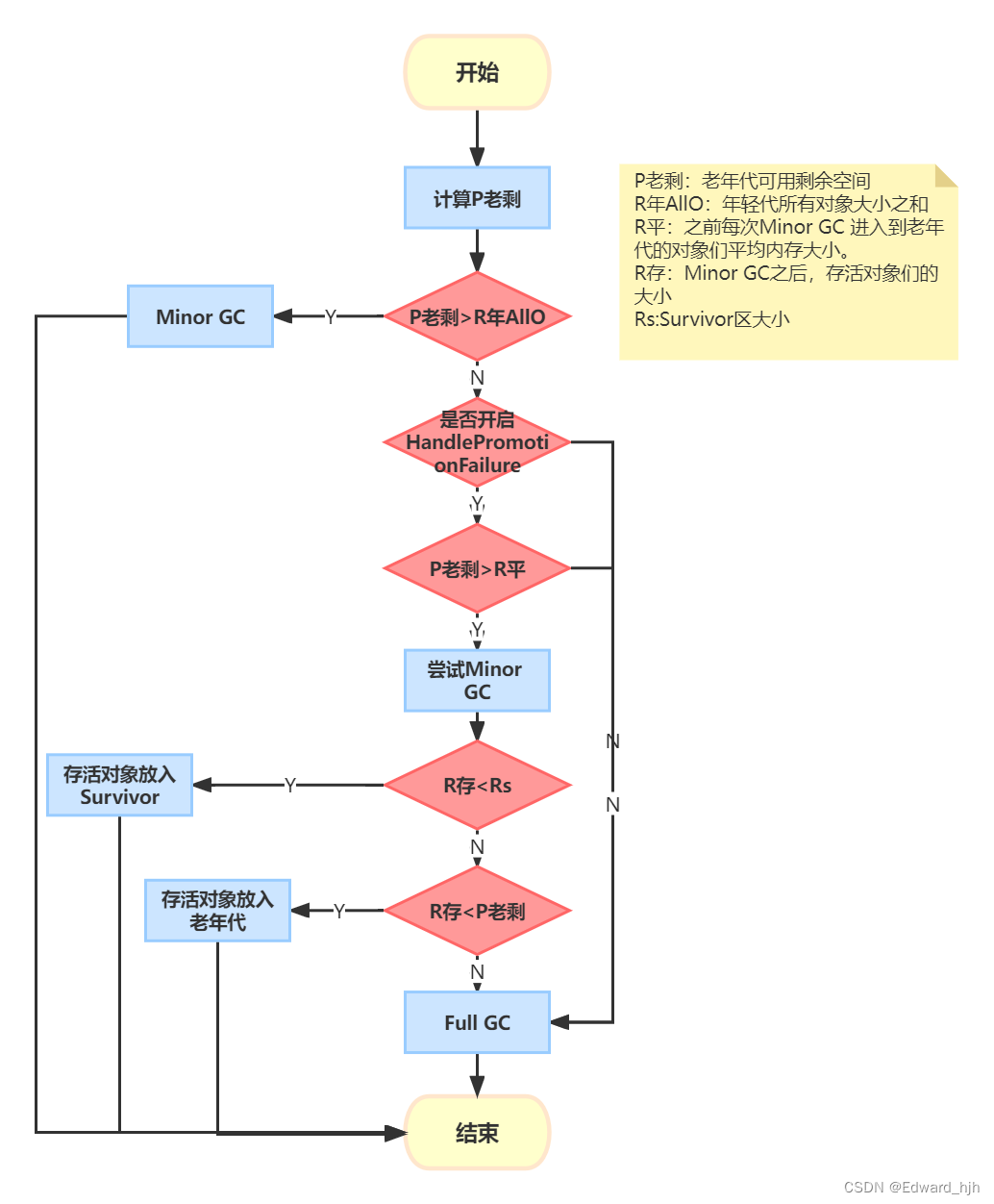
一,JVM 1,JVM区域划分 类装载器,运行时数据区,字节码执行引擎 2,JVM内存模型(运行时数据区) 由本地方法栈,虚拟机栈,堆,方法区,和程序计数器组成。…...
MySQL数据库调优————索引数据结构
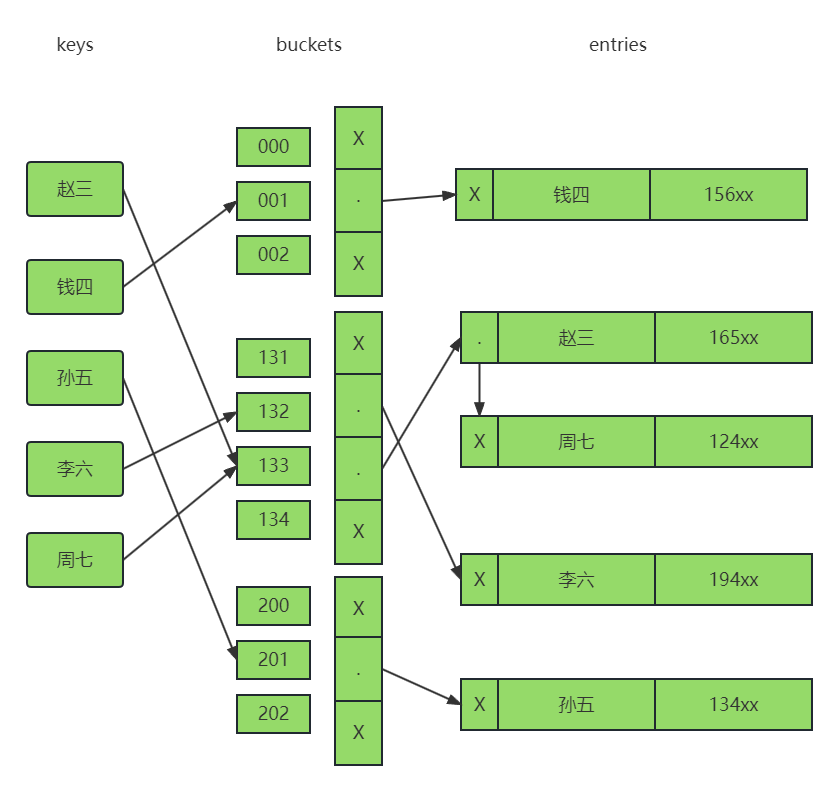
B-TREE B-TREE数据结构 B-TREE特性 根节点的子结点个数2 < X < m,m是树的阶 假设m 3,则根节点可有2-3个孩子 中间节点的子节点个数m/2 < y < m 假设m 3,中间节点至少有2个孩子,最多3个孩子 每个中间节点包含n个关…...

visual studio 改变界面语言
在使用visual studio 2019 时,开始是英文界面,后面变成了中文界面。但是看视频教学时有的是英文界面,我就想回到英文界面,所以有切换界面语言的需要。其实操作很简单:工具-> 选项 打开界面在界面里选择环境…...

2023.2.16每日一题——1250. 检查「好数组」
每日一题题目描述解题核心解法一:数论题目描述 题目链接:1250. 检查「好数组」 给你一个正整数数组 nums,你需要从中任选一些子集,然后将子集中每一个数乘以一个 任意整数,并求出他们的和。 假如该和结果为 1&#x…...

亿级高并发电商项目-- 实战篇 --万达商城项目 八(安装FastDFS、安装Nginx、文件服务模块、文件上传功能、商品功能与秒杀商品等功能)
专栏:高并发---分布式项目 👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信支…...

Viper捐款7000万韩元,合计人民币是多少钱?
Viper捐款7000万韩元,合计人民币是多少钱? #2023LCK春季赛##英雄联盟# #Viper捐款7000万韩元# Viper向大田东区捐款 7000 万,成为大田荣誉协会 105 号会员。Viper选手从 2019 年开始一直向大田东区捐款,但是他不希望这件事被公开…...
前端vue实现系统拦截跳转外链并进入跳转询问界面
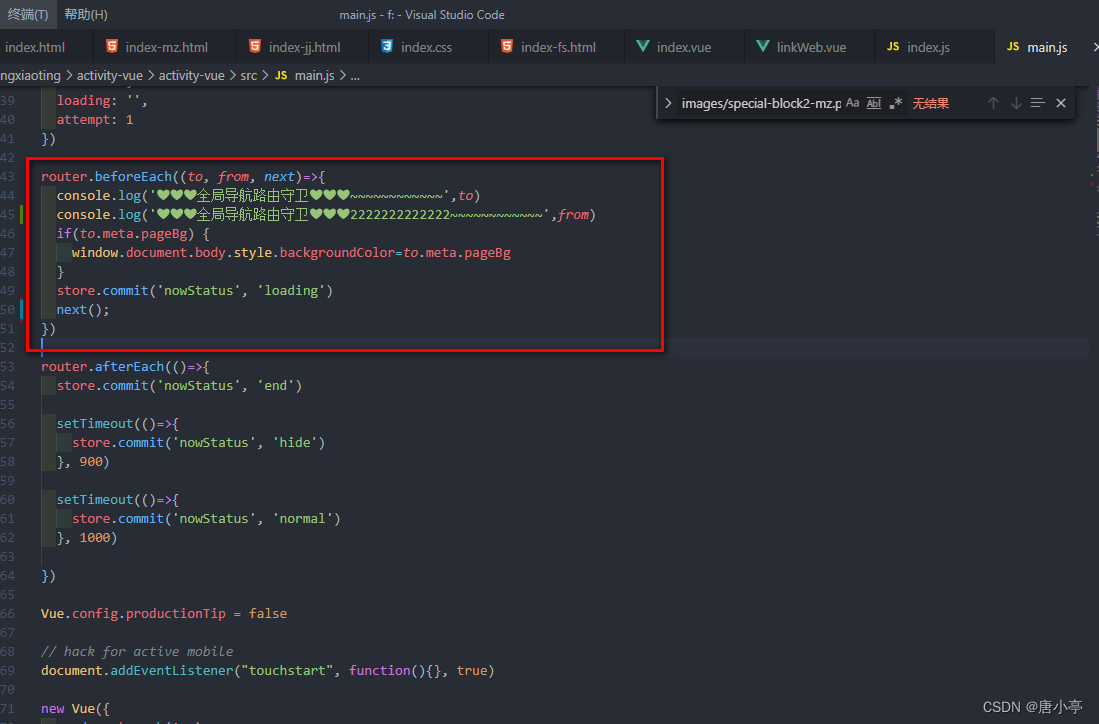
跳转询问界面如下图所示: 给自己挖坑的实现方式,最终解决方案请看最底下 思路:正常情况下我们有2种方式跳转外链 第一种非a标签,我们手动添加事件进行跳转 <div class"dingdan public-padding p-item" click&quo…...
单引号、双引号、不加引号和反引号用法和区别详解)
【Linux】Shell(Bash)单引号、双引号、不加引号和反引号用法和区别详解
简要总结 不加引号:不会将含有空格的字符串视为一个整体输出, 如果内容中有变量等,会先把变量解析出结果,然后在输出最终内容来,如果字符串中带有空格等特殊字符,则不能完整的输出,需要改加双引号ÿ…...

本人使用的idea插件
文章目录🚏 本人使用的idea插件🚬 pojo to Json🚬 GsonFormatPlus🚬 EasyYapi🚬 Chinese (Simplified) Language Pack / 中文语言包🚬 MyBatis Log Free🚬 MyBatisPlusX🚬 Statistic…...

站在行业C位,谷医堂打开健康管理服务新思路
对于农村及贫困地区老百姓来说,由于交通因素和家庭经济条件制约,看病难致身体调理情况一直不太乐观,这也导致心理压力很大。然而,随着近年中医药产业崛起与快速发展,这种局面很快就会得到改观,以湖南谷医堂…...
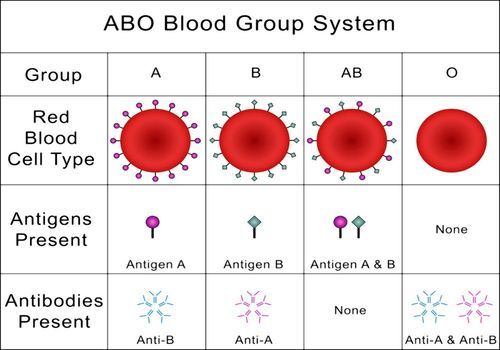
ABO溶血症概率
[简介]ABO溶血是由于母亲和胎儿ABO血型不合引起的新生儿溶血,概率不是很大,一般出现在准妈妈是O血,准爸爸是非O血,这次容易发生血型不合,但新生儿ABO溶血概率不高,大多数症状相对较轻。ABO溶血的概率是什么…...

【算法数据结构体系篇class03】:数组、链表、栈、队列、递归时间复杂度、哈希表、有序表问题
一、反转链表package class03;import java.util.ArrayList; import java.util.List;/*** 链表反转*/ public class ReverseLinkedList {public static class Node {public int value;public Node next;public Node(int data) {value data;}}public static class DoubleNode {p…...
)
【新2023】华为OD机试 - 最多提取子串数目(Python)
最多提取子串数目 题目 给定由 [a-z] 26 个英文小写字母组成的字符串 A 和 B,其中 A 中可能存在重复字母,B 中不会存在重复字母 现从字符串 A 中按规则挑选一些字母,可以组成字符串 B。 挑选规则如下: 1) 同一个位置的字母只能被挑选一次 2) 被挑选字母的相对先后顺序不…...

嵌入式C语言设计模式 --- 代理模式
1 - 什么是代理模式? 代理模式(Proxy Pattern),是指当客户端无法访问某个对象或者访问某个对象存在困难的时候,可以通过一个代理对象来进行间接访问。 举一个生活中的例子,比如,我们在买火车票或者飞机票的时候,有时候不会直接在12306或者航空公司官网上面购买,而是…...

前端性能优化的整理笔记
🚴 前言大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库🏄利用碎片化的时间,系统的整理,性能优化的知识点。🎯 前端性能优化…...
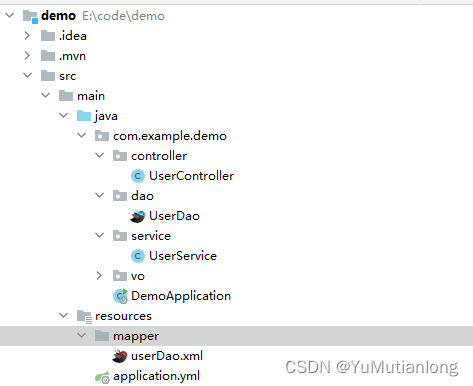
springboot+mybatis连接数据库实现增删改查功能
springbootmybatis连接数据库实现增删改查功能创建表创建项目实体类DAO接口写sql的XML文件Service层Controller启动类结果目录结构参考博客创建表 create table user(id int ,name varchar(30),pwd varchar(40) )insert into user values(2,hxf,789101),(3,hlm,789102),(4,hzh…...

疑似45亿地址信息泄露事件跟进后续
开放隐私计算 收录于合集#数据安全13个开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播,愿成为中国 “隐私计算最后一公里的服务区…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
