滑动窗口 AcWing (JAVA)
给定一个大小为 n≤10^6 的数组。
有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为
[1 3 -1 -3 5 3 6 7],k 为 33。
| 窗口位置 | 最小值 | 最大值 |
|---|---|---|
| [1 3 -1] -3 5 3 6 7 | -1 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | -3 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | -3 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | -3 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | 3 | 6 |
| 1 3 -1 -3 5 [3 6 7] | 3 | 7 |
你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式:
输入包含两行。
第一行包含两个整数 n和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式:
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
解题思路: 如果朴素的做法,将每次得到的窗口进行遍历找最小值。时间复杂度大概是nk,不出意外是会超时的。如何对其进行优化呢?
首先以数组q[N],作为本题队列,a[N]存入输入的元素。我们知道下标和元素具有一 一对应的关系,所以q[i]不是存入元素所对应的值,而是元素所对应的下标。
在这里设hh = 0为头指针,tt = - 1为尾指。
首先应该明确窗口的特点:即内部元素的数量在k的时候即可输出最内部最小值和最大值。此后每移动一下就再次输出一次。这恰好哦可以用循环变量i来表示,如下窗口:
[a,b,c,d.....]
0 i 窗口内部元素的数量可用 (i - 0 + 1)来表示,当窗口内数量够k个的时候即可输出,即i - 0 + 1 >= k即 i >= k - 1。
有趣的是当 0~i + 2 中c为最小值的时候,当窗口向右边移动的时候:
[b,c,d,e.....]
1 i + 1 min = c
[c,d,e,f.....]
2 i + 2 min = c
不难看出窗口在移动的时候,最小值仍是c,如果能用队列存入最小值的下标(即q[tt] = 2),那就避免重新遍历窗口的麻烦。那问题来了设立队列只是为了存入一个最小值的吗?这显然不是,如下窗口继续向右移动:
[d,e,f,g.....]
3 i + 3 min = ? 由此可见如果队列里值只存入c的下标,当窗口不包含c的时候队列内的 q[tt] = 2 也就没用了。
那么需要队列,理想的情况是让队列内存入 最小元素下标,第二小元素下标,第三小元素下标.......
当窗口不再包含最小元素的时候那么就可以在队列内删去了,那么第二小元素就理应成为新的最小元素了,以此类推,队列头部元素一直是符合条件的最小元素下标。
至于如何输出最大值,和上述反着来即可。
理论成立代码如下(未加速版):
import java.util.*;public class Main {public static int N = 1000010;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int a[] = new int [N];//数组int q[] = new int [N];//队列int n = sc.nextInt();int k = sc.nextInt();for(int i = 0; i < n; i ++) a[i] = sc.nextInt();int hh = 0, tt = -1;//队头,队尾,q[hh]存入最小元素下标for(int i = 0; i < n; i ++) {//找最小值if(hh <= tt && q[hh] < i - k + 1) hh ++;//在滑动窗口的外面,移动左窗口while(hh <= tt && a[q[tt]] >=a[i]) tt--;//队尾不比添加进来的数小,那就没用,删掉。q[++ tt] = i;//添加元素。if(i >= k - 1) {if(i == n-1)System.out.println(a[q[hh]]);elseSystem.out.print(a[q[hh]]+" "); } }
//输出最大值hh = 0; tt = -1;for(int i = 0; i < n; i ++) {if(hh <= tt && q[hh] < i - k + 1 ) hh ++;while(hh <= tt && a[q[tt]] <= a[i]) tt --;q[++ tt] = i;if(i >= k - 1) {if(i == n - 1)System.out.print(a[q[hh]]);elseSystem.out.print(a[q[hh]]+" ");}}}
}由于最后一个数据过于庞大,时间超时了,想通过,得用如下的加速版:
import java.io.*;
import java.util.*;;
public class Main {public static int N = 1000010;public static void main(String[] args) throws IOException {// TODO Auto-generated method stubScanner sc = new Scanner(new BufferedInputStream(System.in));BufferedWriter sout = new BufferedWriter(new OutputStreamWriter(System.out));int a[] = new int [N];//数组int q[] = new int [N];//队列int n = sc.nextInt();int k = sc.nextInt();for(int i = 0; i < n; i ++) a[i] = sc.nextInt();int hh = 0, tt = -1;//队头,队尾,q[hh]存入最小元素下标for(int i = 0; i < n; i ++) {//找最小值if(hh <= tt && q[hh] < i - k + 1) hh ++;//在滑动窗口的外面,移动左窗口while(hh <= tt && a[q[tt]] >=a[i]) tt--;//队尾不比添加进来的数小,那就没用,删掉。q[++ tt] = i;//添加元素。if(i >= k - 1) {sout.write(a[q[hh]]+" "); } }sout.write("\n");//输出最大值hh = 0; tt = -1;for(int i = 0; i < n; i ++) {if(hh <= tt && q[hh] < i - k + 1 ) hh ++;while(hh <= tt && a[q[tt]] <= a[i]) tt --;q[++ tt] = i;if(i >= k - 1) {sout.write(a[q[hh]]+" ");}}sout.close();sc.close();}}相关文章:
)
滑动窗口 AcWing (JAVA)
给定一个大小为 n≤10^6 的数组。 有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。 你只能在窗口中看到 k 个数字。 每次滑动窗口向右移动一个位置。 以下是一个例子: 该数组为 [1 3 -1 -3 5 3 6 7],k 为 33。 窗口位置最小值最大…...
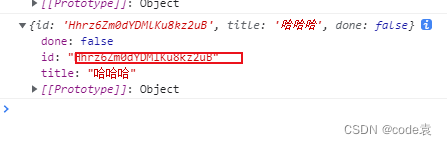
vue小案例
vue小案例 组件化编码流程 1.拆分静态组件,按功能点拆分 2.实现动态组件 3.实现交互 文章目录vue小案例组件化编码流程1.父组件给子组件传值2.通过APP组件给子组件传值。3.案例实现4.项目小细节1.父组件给子组件传值 父组件给子组件传值 1.在父组件中写好要传的值&a…...

阅读笔记3——空洞卷积
空洞卷积 1. 背景 空洞卷积(Dilated Convolution)最初是为解决图像分割的问题而提出的。常见的图像分割算法通常使用池化层来增大感受野,同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图先缩小再放大的过程造成了精…...
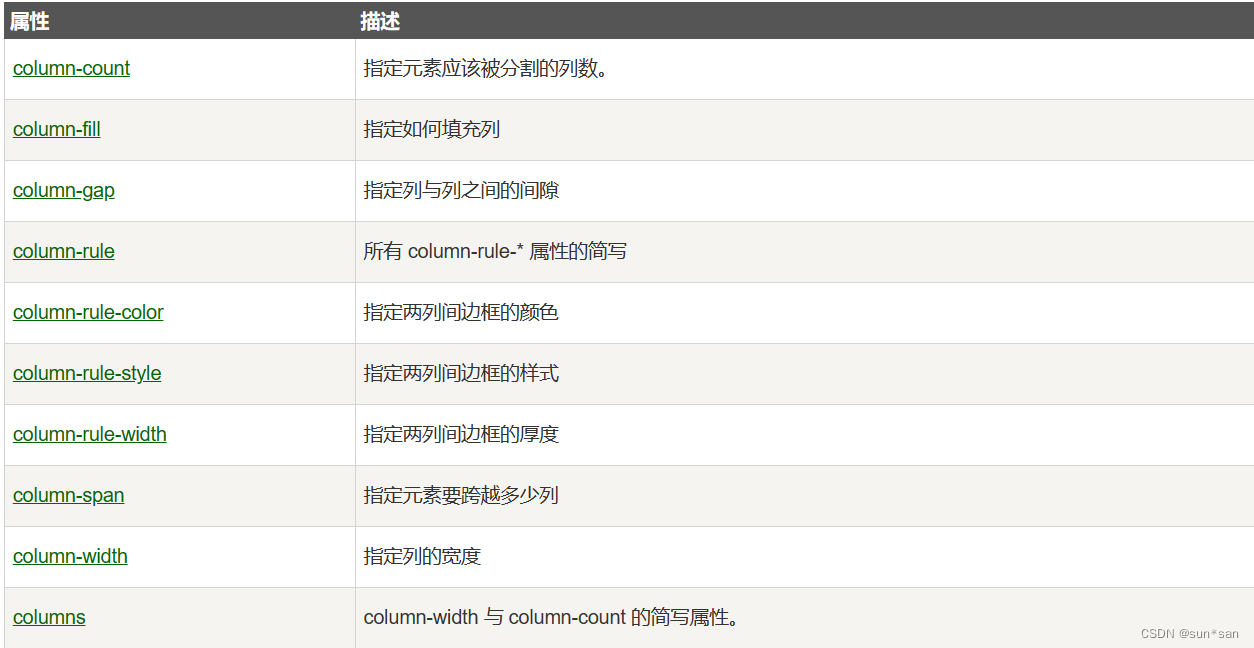
CSS系统学习总结
目录 CSS边框 CSS背景 CSS3渐变 线性渐变(Linear Gradients)- 向下/向上/向左/向右/对角方向 语法 线性渐变(从上到下) 线性渐变(从左到右) 线性渐变(对角) 使用角度 使用多…...

阿里一面:你做过哪些代码优化?来一个人人可以用的极品案例
前言 在尼恩读者50交流群中,尼恩经常指导小伙伴改简历。 改简历所涉及的一个要点是: 在 XXX 项目中,完成了 XXX 模块的代码优化 另外,在面试的过程中,面试官也常常喜欢针对提问,来考察候选人对代码质量的追…...
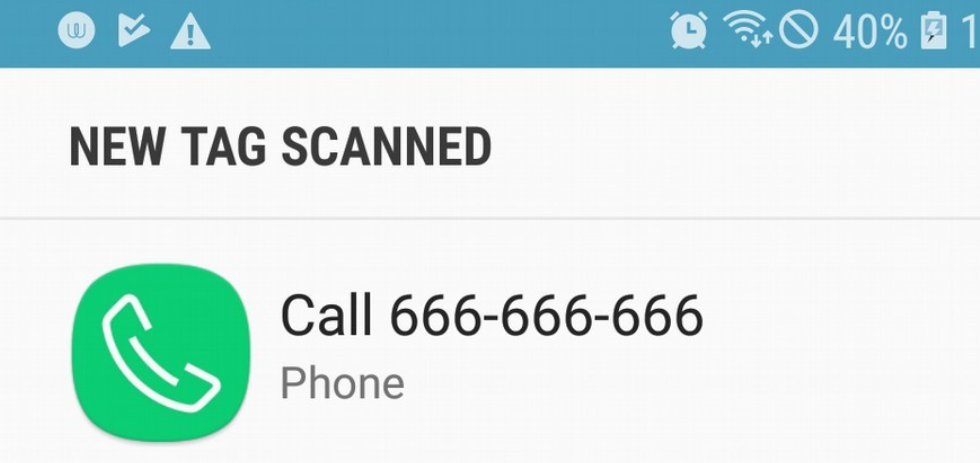
Android NFC 标签读写Demo与历史漏洞概述
文章目录前言NFC基础1.1 RFID区别1.2 工作模式1.3 日常应用NFC标签2.1 标签应用2.2 应用实践2.3 标签预览2.4 前台调度NFC开发3.1 NDEF数据3.2 标签的调度3.3 读写Demo3.4 Demo演示历史漏洞4.1 中继攻击4.2 预览伪造4.3 篡改卡片4.4 其它漏洞总结前言 NFC 作为 Android 手机一…...

亿级高并发电商项目-- 实战篇 --万达商城项目 六(编写角色管理、用户权限(Spring Security认证授权)、管理员管理等模块)
专栏:高并发---前后端分布式 👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信…...

博视像元获近5000万元融资,主攻半导体前道及锂电高端部件供应
这两年各大车企与电池厂商都在快速新建产能,尤其上游原材料成本大增,反映到产业链上巨头都在寻求增效,高端制造技术投入也大幅增长。比如这家,高端工业相机提供商「博视像元」近期宣布完成近5000万的天使加轮融资,投资…...

SpringCloud-断路器Hystrix
一、降级使用1、添加依赖<!--hystrix--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-hystrix</artifactId></dependency>2、启动类添加注解EnableCircuitBreakerSpringBoot…...

JavaScript精简笔记
文章目录基础语法函数1.1、函数的使用预解析对象1.1、创建对象基础语法 函数 1.1、函数的使用 函数在使用时分为两步:声明函数和调用函数 ①声明函数 //声明函数 function 函数名(){//函数体代码 }function 是声明函数的关键字,必须小写由于函数一般是为了实现…...

MySQL常用函数汇总
1 MySQL 字符串函数函数描述实例ASCII(s)返回字符串 s 的第一个字符的 ASCII 码。返回 CustomerName 字段第一个字母的 ASCII 码:SELECT ASCII(CustomerName) AS NumCodeOfFirstCharFROM Customers;CHAR_LENGTH(s)返回字符串 s 的字符数返回字符串 RUNOOB 的字符数S…...
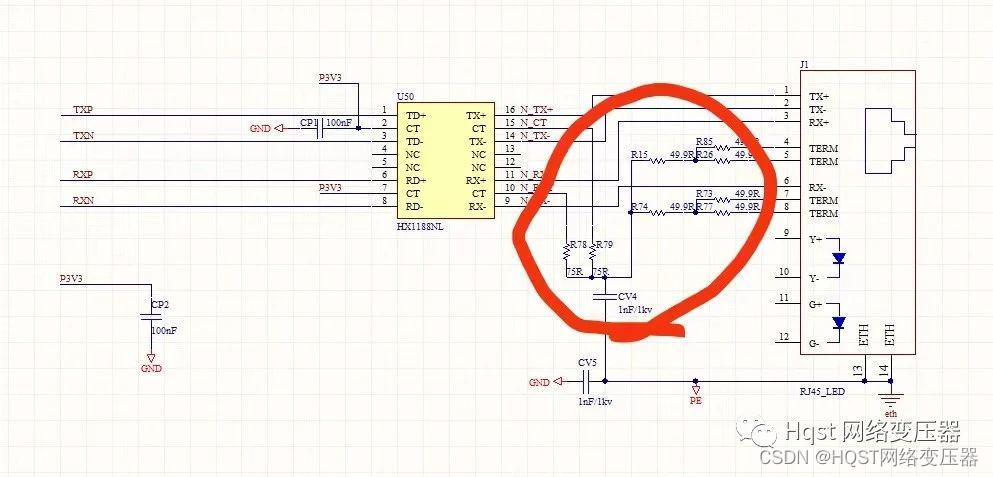
100M网口客户电脑插上网线就断线,自己工厂正常,是什么问题导致?
Hqst(华强盛科技)导读:物联工程师100M网口产品出现客户电脑插上网线就显示断线,无法通信,在自己工厂又正常使用,是什么问题?问:100M 网口, 使用改电路, 产品出…...

从零开始学习无人机 00 硬件配置
遥控器 型号 乐迪Radiolink AT9S Pro 固件更新 对遥控器固件作更新 乐迪Radiolink AT9S Pro 固件更新 光流传感器 型号 思动智能ThoneFlow-3901U 开发文档 Pmw3901光流传感器PX4开发文档 距离传感器 型号 空循环Nooploop TOFSense-F Pro 开发文档 TOFSense-F官方…...
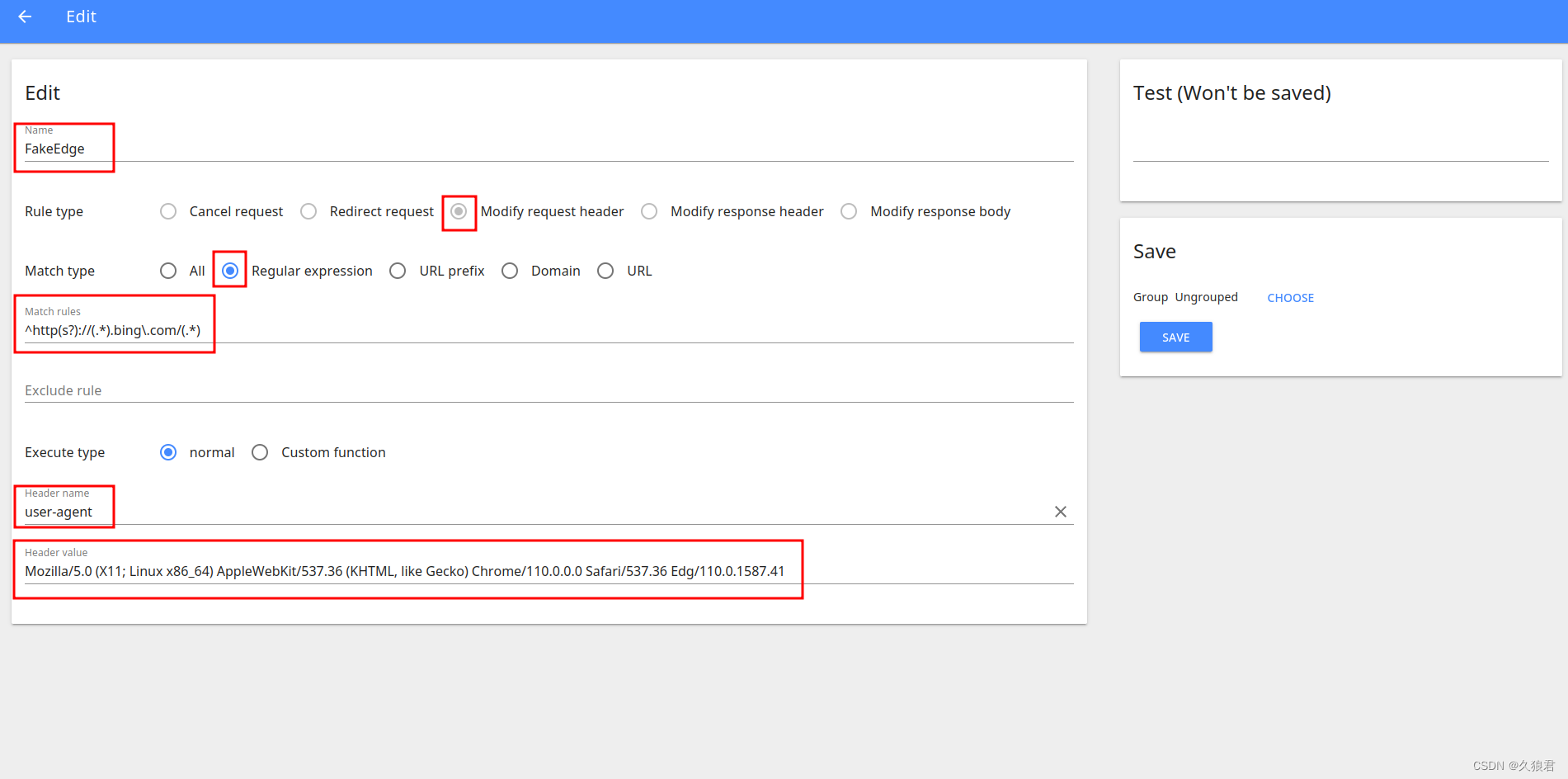
免翻在Chrome上使用新必应(New Bing)聊天机器人
这里不讲如何加入New Bing内测 文章目录免翻使用New Bing用Chrome(非Edge)使用新必应聊天机器人免翻使用New Bing 第一个是免翻,需要一个浏览器插件Header Editor,扩展商店或者百度自行下载安装吧。打开该插件,添加一个规则 为方便填写&…...

LA@特征值和特征向量
文章目录特征值和特征向量例例求解方阵的特征值和特征向量🎈特征多项式特征方程方阵特征值和特征向量的性质证明推论衍生特征值更一般的转置和特征值其他结论(方阵多项式的特征值与方阵本身特征值的关系)特征向量线性相关性特征值和特征向量 许多定量分析模型中,常常…...
transpose代码学习
论文:TransPose: Keypoint Localization via Transformer Sen Yang Zhibin Quan Mu Nie Wankou Yang* School of Automation, Southeast University, Nanjing 210096, China {yangsenius, 101101872, niemu, wkyang}seu.edu.cn 下载地址:https://arxiv.o…...
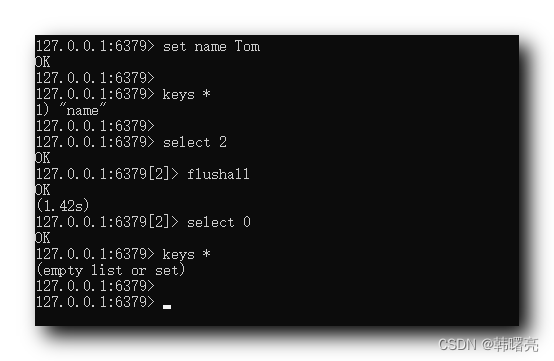
【Redis】Redis 常用数据类型操作 ② ( 数据库操作 | 切换数据库 | 查询当前数据库键个数 | 清空当前数据库 | 清空所有数据库 )
文章目录一、Redis 数据库操作1、切换数据库2、查询当前数据库键个数3、清空当前数据库4、清空所有数据库一、Redis 数据库操作 在之前的博客 【Redis】Redis 数据库 安装、配置、访问 ( Redis 简介 | 下载 Redis 安装包 | 安装 Redis 数据库 | 命令行访问 Redis | 使用可视化工…...
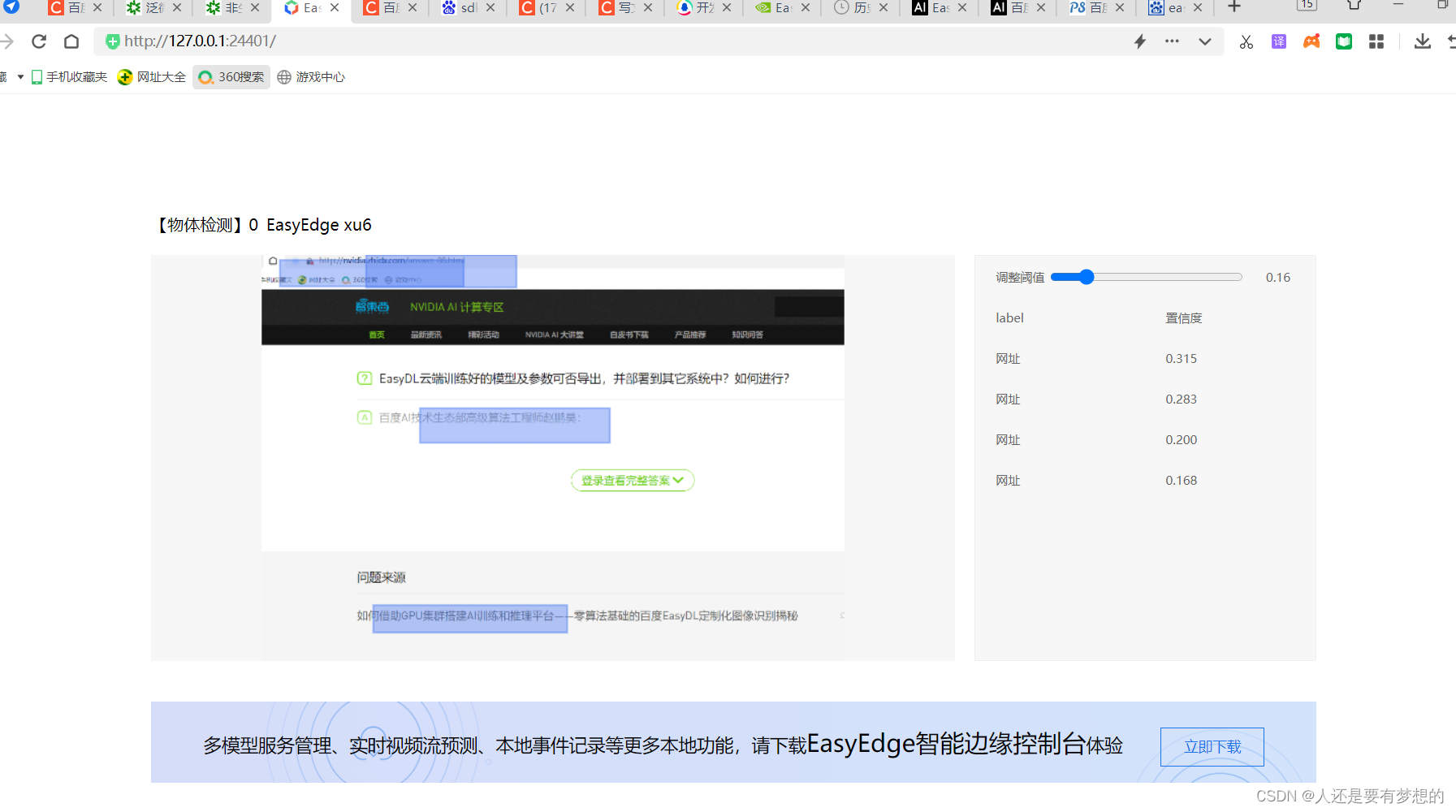
最简单的物体识别例子
第一步下载百度EASYDL工具。 网址EasyDL 图像 然后下载本地训练工具包: 本地下载,运行。 首先创建数据集, 完成,创建目标任务。 选择物体检测创建任务 选择训练,将数据集引入 通用型小型设备SDK 选择这个可以本地直…...

指针——“C”
各位CSDN的uu们你们好呀,今天,小雅兰学习的内容是指针,这次只会讲一些很简单的知识点,更详细的指针知识会在以后的博客中逐步剖析清楚,那么现在,就让我们进入指针的世界吧 指针是什么 指针和指针类型 野指…...

学习 Linux 内核书籍推荐
原文链接,欢迎关注: 你为什么学习 Linux 内核? - CodeAllen的回答 - 知乎 https://www.zhihu.com/question/31369673/answer/2894981254 主要是工作需要,其实对于我自己的工作来说,在Linux开发的具体业务和算法才是重…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
