LDA算法实现鸢尾花数据集降维
目录
- 1. 作者介绍
- 2. LDA降维算法
- 2.1 基本概念
- 2.2 算法流程
- 3. LDA算法实现
- 3.1 数据集介绍
- 3.2 代码实现
- 3.3 结果展示
1. 作者介绍
唐杰,男,西安工程大学电子信息学院,2022级研究生
研究方向:机器视觉与人工智能
电子邮件:3225033259@qq.com
陈梦丹,女,西安工程大学电子信息学院,2022级硕士研究生,张宏伟人工智能课题组
研究方向:机器视觉与人工智能
电子邮件:1169738496@qq.com
2. LDA降维算法
2.1 基本概念
线性判别分析(Linear Discriminant Analysis,LDA)是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同,LDA是一种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想:多维空间中,数据处理分类问题较为复杂,LDA算法将多维空间中的数据投影到一条直线上,将d维数据转化成1维数据进行处理。对于训练数据,设法将多维数据投影到一条直线上,同类数据的投影点尽可能接近,异类数据点尽可能远离。对数据进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定样本的类别。
如果用一句话概括LDA思想,即“投影后类内方差最小,类间方差最大”。
2.2 算法流程
LDA算法流程如下:

3. LDA算法实现
3.1 数据集介绍
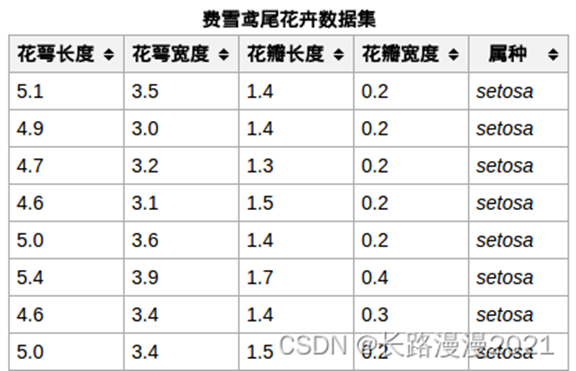
Iris数据集的中文名是安德森鸢尾花卉数据集,英文全称是Anderson’s Iris data set。Iris包含150个样本,对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息,所以Iris数据集是一个150行5列的二维表。
通俗地说,Iris数据集是用来给花做分类的数据集,每个样本包含了花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征(前4列),我们需要建立一个分类器,分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾(这三个名词都是花的品种)。
Iris的每个样本都包含了品种信息,即目标属性(第5列,也叫target或label)。如下所示:
3.2 代码实现
import numpy as np
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt2# 定义LDA类
class LDA:def __init__(self, n_components=2, kernel='rbf', gamma=400):self.n_components = n_componentsself.kernel = kernelself.gamma = gammadef fit(self, X, y):# 计算内部和外部类别散度矩阵X_mean = np.mean(X, axis=0)S_W = np.zeros((X.shape[1], X.shape[1]))S_B = np.zeros((X.shape[1], X.shape[1]))for i in range(3):X_class = X[y == i, :]X_class_mean = np.mean(X_class, axis=0)S_W += np.dot((X_class - X_class_mean).T, (X_class - X_class_mean))S_B += len(X_class) * np.dot((X_class_mean - X_mean).reshape(-1, 1), (X_class_mean - X_mean).reshape(1, -1))# 使用LDA算法计算投影矩阵Weig_val, eig_vec = np.linalg.eig(np.dot(np.linalg.inv(S_W), S_B))idx = np.argsort(-eig_val.real)self.W = eig_vec[:, idx[:self.n_components]]# 归一化处理scaler = MinMaxScaler()self.W = scaler.fit_transform(self.W)def transform(self, X):# 投影到特征空间X_new = np.dot(X, self.W)# 归一化处理scaler = MinMaxScaler()X_new = scaler.fit_transform(X_new)return X_new# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target# 模型训练
lda = LDA(n_components=2, kernel='rbf')
lda.fit(X, y)# 数据转换
X_new = lda.transform(X)# 可视化降维前的数据分布
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()# 可视化降维后的数据分布
plt2.scatter(X_new[:, 0], X_new[:, 1], c=y)
plt2.show()
3.3 结果展示
运行结果如下:
图一 鸢尾花数据集前两维分布图

图二 降维后数据分布图

相关文章:

LDA算法实现鸢尾花数据集降维
目录 1. 作者介绍2. LDA降维算法2.1 基本概念2.2 算法流程 3. LDA算法实现3.1 数据集介绍3.2 代码实现3.3 结果展示 1. 作者介绍 唐杰,男,西安工程大学电子信息学院,2022级研究生 研究方向:机器视觉与人工智能 电子邮件ÿ…...

深入理解Linux虚拟内存管理
系列文章目录 Linux 内核设计与实现 深入理解 Linux 内核(一) 深入理解 Linux 内核(二) Linux 设备驱动程序(一) Linux 设备驱动程序(二) Linux 设备驱动程序(三…...
自动化测试框架、Python面向对象以及POM设计模型简介
目录 1 自动化测试框架概述 2 自动化测试框架需要的环境 3 自动化测试框架设计思想:Python面向对象 4 自动化测试框架设计思想:POM(Page Object Model)页面对象模型 1 自动化测试框架概述 所谓的框架其实就是一个解决问题…...
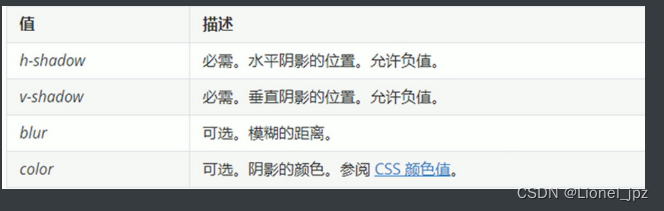
【CSSpart4--盒子模型】
CSSpart4--盒子模型 网页布局的三大核心:盒子模型,浮动,定位网页布局的过程(本质):盒子模型的组成四部分:边框,内容,内边距,外边距 一 、盒子边框border:1.1 …...
Linux - Java 8 入门安装与重装教程集锦
一、入门初始安装 1. 具体安装教程 1. linux 系统中如何安装java环境(通过tar.gz文件) 安装包下载链接 Java 的 tar.gz 安装包下载链接传送门 Linux 系统的 Java 环境变量配置教程 1. linux查看java版本,以及配置java home 2. Linux环…...
2023年最新企业网盘排行榜出炉
随着云计算技术的不断发展,企业日常工作中大量的资料、文档等信息需要实现集中管理,此时企业网盘工具就应运而生。企业网盘是一种可用于企业内部管理、团队协作及文件共享的云存储平台,能够极大提高企业办公效率和安全性。 一、企业网盘的帮助…...

C++内存分类
内存分配方式(内存布局): 内存5分类 堆、栈、自由存储区、全局/静态存储区、常量存储区 (1)栈:内存由编译器在需要时自动分配和释放。通常用来存储局部变量和函数参数,函数调用后返回的地址。(为运行函数而…...

不是说00后已经躺平了吗,怎么还是这么卷.....
都说00后已经躺平了,但是有一说一,该卷的还是卷。 前段时间我们部门就来了个00后,工作都还没两年,跳到我们公司起薪20K,都快接近我了。 后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。最近和…...

国内免费版ChatGPT
目录 前言:网站大全 1. ChatGPT是什么 2. ChatGPT的发展历程 3. ChatGPT对程序员的影响 4. ChatGPT对普通人的影响 5. ChatGPT的不足之处 前言:网站大全 AI文本工具站 (laicj.cn) ——gpt-3.5 功能强大(推荐) Chatgpt在线网页版-…...

常用本地事务和分布式事务解决方案模型
目录 1 DTP模型2 2PC2.1 方案简介2.2 处理流程2.2.1 阶段1:准备阶段2.2.2 阶段2:提交阶段 2.3 方案总结 3 3PC3.1 方案简介3.2 处理流程3.2.1 阶段1:canCommit3.2.2 阶段2:preCommit3.3.3 阶段3:do Commit 3.3 方案总结…...

无代码玩转GIS应用,我也在行【文末送书】
您好,我是码农飞哥(wei158556),感谢您阅读本文,欢迎一键三连哦。💪🏻 1. Python基础专栏,基础知识一网打尽,9.9元买不了吃亏,买不了上当。 Python从入门到精通…...
xlsx是什么格式
xlsx是什么格式? xlsx是Excel文档的扩展名,其基于Office Open XML标准的压缩文件格式,取代了其以前专有的默认文件格式,在传统的文件名扩展名后面添加了字母x,即.xlsx取代.xls。 xlsx文件是什么格式? xlsx是Excel表格的文件格…...

将 Maven 配置为使用阿里云镜像
将 Maven 配置为使用阿里云镜像的步骤如下: 打开 Maven 的 settings.xml 文件:在 Maven 安装目录下的 conf 文件夹中,找到 settings.xml 文件,并打开它。 添加镜像配置:在 settings.xml 文件中,找到 <m…...
行业报告 | 2022文化科技十大前沿应用趋势(下)
原创 | 文 BFT机器人 04 商业创新 趋势7:区块链技术连接传统文化,数字藏品市场在探索中发展 核心内容: 2022年,数字藏品在区块链技术的助力下应运而生。狭义的数字藏品是指使用区块链技术、基于特定的文化资源所生成唯一的数字凭…...
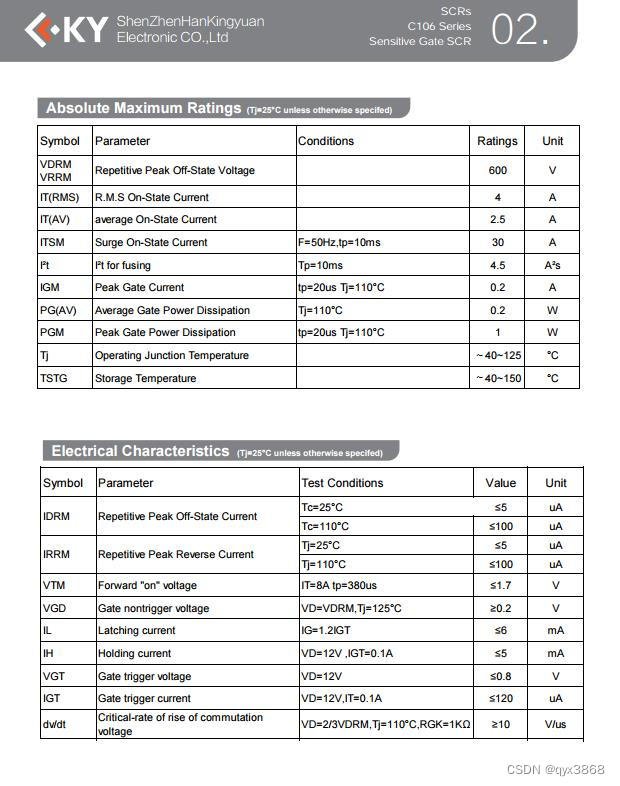
ASEMI代理韩景元可控硅C106M参数,C106M封装,C106M尺寸
编辑-Z 韩景元可控硅C106M参数: 型号:C106M 断态重复峰值电压VDRM:600V 通态电流IT(RMS):4A 通态浪涌电流ITSM:30A 平均栅极功耗PG(AV):0.2W 峰值门功率耗散PGM:1W 工作接点温度Tj&…...

ChatGPT资料汇总学习
🧠 Awesome-ChatGPT ChatGPT资料汇总学习,持续更新… ChatGPT再一次掀起了AI的热潮,是否还会像BERT一样成为AI进程上的里程碑事件,还是噱头炒作,持续关注,让时间流淌~ ChatGPT免费体验入口网址 http://c…...

什么是垂直扩容和水平扩容
垂直扩容和水平扩容是架构设计中常用的两种扩容方式,它们各有优势,应根据具体场景选择合适的扩容方式。 1.垂直扩容 垂直扩容是通过增加单个节点的处理能力来提高整个系统的性能,通常是通过增加服务器的硬件配置、升级CPU、内存、硬盘等来实…...
Fiddler抓不到包Fiddler chrome Edge无法抓包原因排查Fiddler死活抓不了包
一、问题描述 我这电脑上的Fiddler莫名其妙的死活就是无法抓包,换了几个版本的Fiddler都没有解决,这里参考了一些网上的教程,最终解决了,该文章算是比较详细的一篇介绍Fiddler无法抓包的教程。无法抓包主要由以下原因导致的&#…...

11. TCP并发网络编程
本文主要介绍TCP并发网络的编程,重点介绍io多路复用的epoll实现 一、TCP/IP 网络通信过程 要完成一个完整的 TCP/IP 网络通信过程,需要使用一系列函数来实现。这些函数包括 bind、listen、accept 和 recv/send 等。下面是它们的配合流程: 创…...
[GUET-CTF2019]number_game[数独]
目录 题目 学到的知识点: 题目 在buu上看到了一道数独题,没见过,记录一下 下载附件,查壳,无壳,在IDA中打开,直接找到主函数 unsigned __int64 __fastcall main(int a1, char **a2, char **a3…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
