SVD求解两组多维点之间的欧式变换矩阵,及halcon代码实现
之前研究了二维点的仿射变换,用解矩阵的方式求解了两组二维点之间的变换矩阵。
学习了下SVD,看到可以用SVD求解两组多维点之间的欧式变换矩阵,当然也是个最优化问题。
这里的变换只有平移和旋转,没有缩放。
一、先说结论:
现在有两组点(2d,3d,或者多维都可以),
需要找到R和t,使得
一般没有完美解,需要找到最优解R和t,使得P'变换后的点和P误差最小。
操作步骤:
1,,求两组点质心位置,得到两组点去质心坐标
2,得到矩阵W
3,对W进行奇异值分解
4.得到最优R和T
二、用halcon代码来实现下
举例测试两组点P和Q
PX := [0.2,0.4,0.2,0.3]
PY := [0.4,0.6,0.8,0.6]
PZ := [0.6,0.8,0.6,0.5]
QX := [0.25,0.44,0.61,0.3]
QY := [0.32,0.56,0.82,0.4]
QZ := [0.4,0.18,0.6,0.51]
halcon代码实现如下
*两组3d点P和Q,每组4个点PX := [0.2,0.4,0.2,0.3]
PY := [0.4,0.6,0.8,0.6]
PZ := [0.6,0.8,0.6,0.5]
QX := [0.25,0.44,0.61,0.3]
QY := [0.32,0.56,0.82,0.4]
QZ := [0.4,0.18,0.6,0.51]*对P和Q去质心化处理
create_matrix (3, |PX|, [PX,PY,PZ], P)
mean_matrix (P, 'rows', PMean)
create_matrix(1,|PX|,1,Ones)
mult_matrix (PMean, Ones, 'AB', PSub)
sub_matrix(P,PSub,PShift)create_matrix(3,|QX|,[QX,QY,QZ],Q)
mean_matrix(Q,'rows', QMean)
create_matrix (1, |QX|, 0, Ones)
mult_matrix (QMean, Ones, 'AB', QSub)
sub_matrix (Q, QSub, QShift)*得到步骤2里的W矩阵,这里是3维点,左右W是个3*3矩阵
create_matrix (3, 3, 0, W)
for Index := 0 to |PX|-1 by 1get_sub_matrix (PShift, 0, Index, 3, 1, PVec)get_sub_matrix (QShift, 0, Index, 3, 1, QVec)transpose_matrix_mod (QVec)mult_matrix (PVec, QVec, 'AB', PQ)add_matrix_mod (W, PQ)
endfor*对W进行svd分解
svd_matrix (W, 'full', 'both', U, S, V)*计算R
transpose_matrix_mod(U)
mult_matrix (V, U, 'AB', R)*计算R的行列式是否为1
determinant_matrix (R, 'general', Value)
if (Value < 0)get_value_matrix (V, [0,1,2], [2,2,2], Value1)set_value_matrix (V, [0,1,2], [2,2,2], [-Value1[0],-Value1[1],-Value1[2]])mult_matrix (V, U, 'AB', R)
endif*计算t
mult_matrix (R, PMean, 'AB', RPMean)
sub_matrix(QMean,RPMean,t)*得到最后的变换矩阵3*4
create_matrix(3,4,0,HomMat3DID)
set_sub_matrix (HomMat3DID, R, 0, 0)
set_sub_matrix(HomMat3DID, t, 0, 3)
get_full_matrix (HomMat3DID, HomMat3D)得到的变换矩阵为
[-0.65053, 0.436583, 0.621455, -0.0714635, 0.519911, 0.852471, -0.0546402, -0.095308, -0.553627, 0.287556, -0.781542, 0.890677]
三、证明过程
证明过程内容有点多,晚点整理整理再写
参考文章
三维重建(4)之SVD求解三维变换矩阵Rt(旋转+平移)_svd分解求旋转平移矩阵_明月醉窗台的博客-CSDN博客
使用SVD来求解优化问题最优值 - 知乎
相关文章:
SVD求解两组多维点之间的欧式变换矩阵,及halcon代码实现
之前研究了二维点的仿射变换,用解矩阵的方式求解了两组二维点之间的变换矩阵。 学习了下SVD,看到可以用SVD求解两组多维点之间的欧式变换矩阵,当然也是个最优化问题。 这里的变换只有平移和旋转,没有缩放。 一、先说结论&#…...
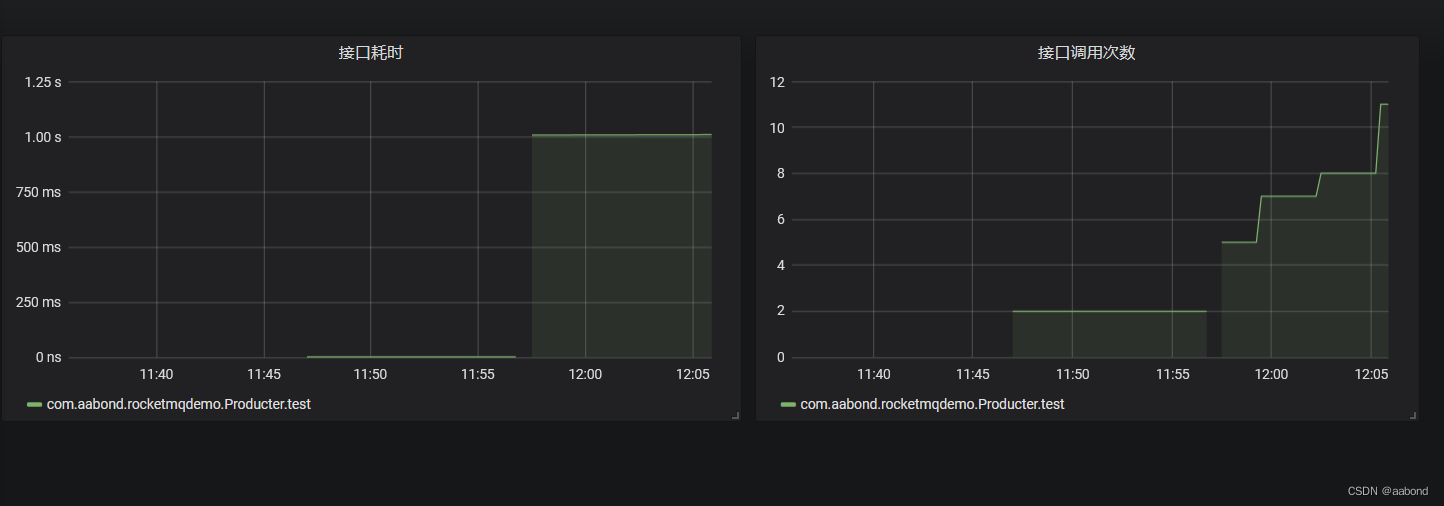
常用监控方案 Prometheus + Grafana 简单使用小结
文章目录 前言一、概念1.1 发展1.2 时序数据1.3 Metric 二、Prometheus2.1 架构2.2 配置2.3 查询语言PromQL2.4 Exporter 三、Grafana3.1 数据源3.2 权限3.3 面板可视化3.4 仪表盘 四、实战4.1 监控 Windows/Linux4.2 监控 JVM4.3 监控 MySQL4.4 监控 Springboot API 参考 前言…...

基于长短期神经网络LSTM的飞行轨迹跟踪预测,基于长短期神经网络LSTM的三维路径预测
目录 背影 摘要 LSTM的基本定义 LSTM实现的步骤 基于长短期神经网络LSTM的飞行轨迹跟踪 完整代码: https://download.csdn.net/download/abc991835105/87705046 效果图 结果分析 展望 参考论文 背影 路径追踪预测,对实现自动飞行驾驶拥有重要意义,长短期神经网络是一种改进…...
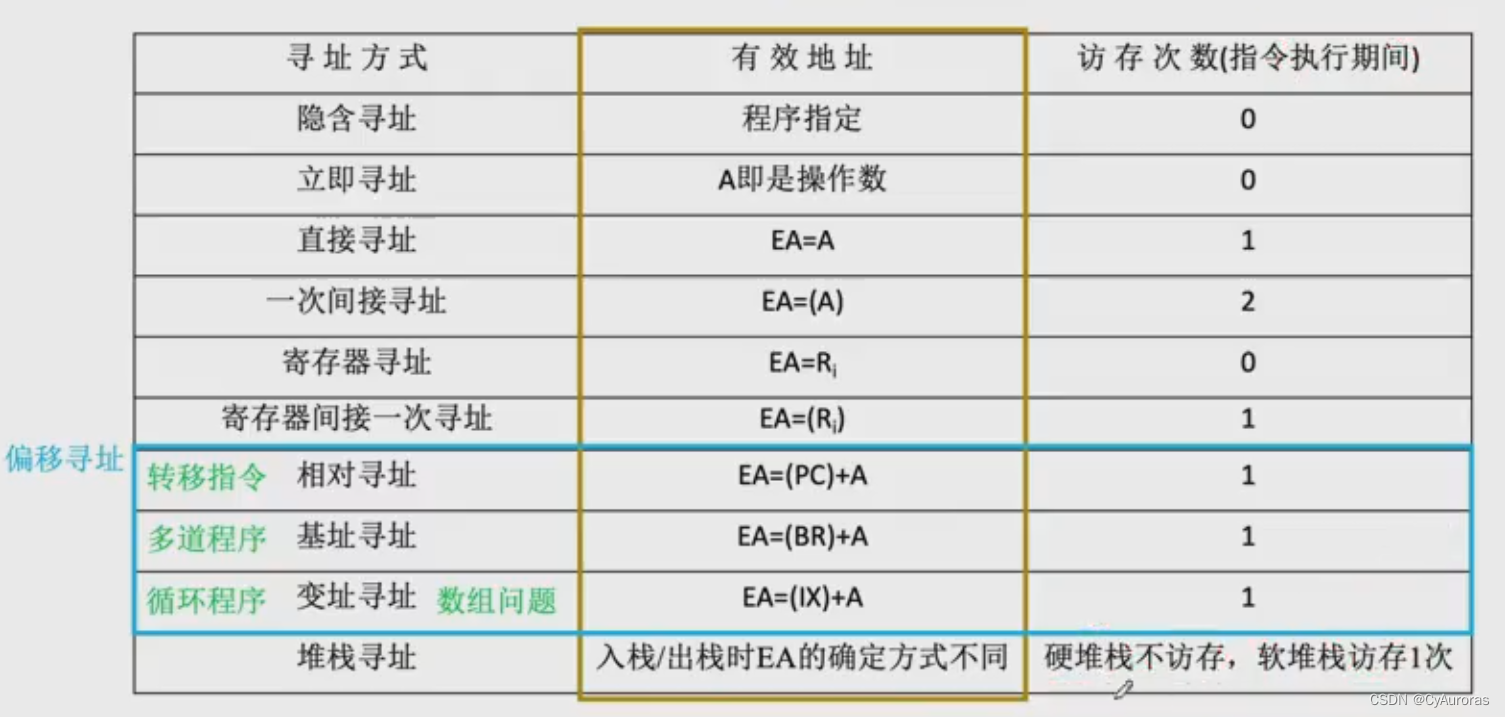
计算机组成原理-指令系统-指令格式及寻址方式
目录 一、指令的定义 1.1 扩展操作码指令格式 二、指令寻址方式 2.1 顺序寻址 2.2 跳跃寻址 三、 数据寻址 3.1 直接寻址 3.2 间接寻址 3.3 寄存器寻址 3.4 寄存器间接寻址 3.5 隐含寻址 3.6 立即寻址 3.7 偏移地址 3.7.1 基址寻址 3.7.2 变址寻址 3.7.3 相对寻址…...

【满分】【华为OD机试真题2023B卷 JAVAJS】经典屏保
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里 经典屏保 知识点循环迭代编程基础 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: DVD机在视频输出时,为了保护电视显像管,在待机状态会显示“屏保动画”,如下图所示,DVD Logo在屏幕内来回运动,碰到边缘会反弹…...

Apache 网页与安全优化
目录 一:Apache网页优化概述 1、概述 2、优化内容 3、gzip介绍 4、Apache的压缩模块 5、mod_ gzip 模块与mod_ deflate 模块 二: 网页压缩 1.检查是否安装 mod_deflate 模块 2. 如果没有安装mod_deflate 模块,重新编译安装 Apache 添…...

Unity的IFilterBuildAssemblies:深入解析与实用案例
Unity IFilterBuildAssemblies Unity IFilterBuildAssemblies是Unity引擎中的一个非常有用的功能,它可以让开发者在构建项目时自定义哪些程序集需要被包含在构建中,哪些程序集需要被排除在建之外。这个功能可以帮助开发者更好地控制项目的构建过程&…...
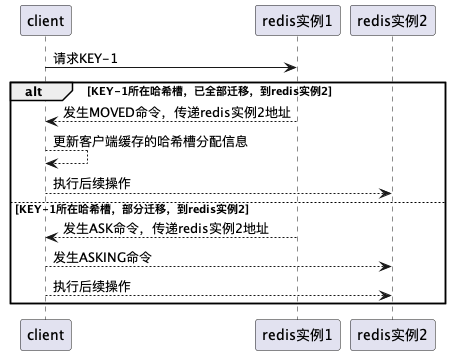
分片架构,Redis Cluster 分析
分片架构解决的问题 通过堆机器,提升读写性能,与存储性能 分片架构设计要点 分片规则 选择Cardinality大的作为分片键,尽可能保证数据分布均匀 常见分片键: 基于主键(业务型数据),基于时间…...

Linux-0.11 文件系统bitmap.c详解
Linux-0.11 文件系统bitmap.c详解 模块简介 该模块包含了两对函数,第一对是和i节点相关的free_inode()和new_inode()。第二对是和逻辑块相关的free_block()和new_block()。 函数详解 free_block void free_block(int dev, int block)该函数的作用是释放设备dev…...
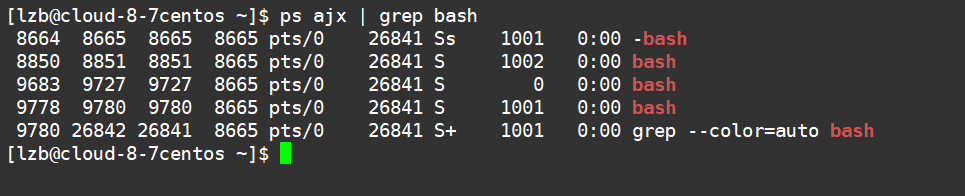
【Linux】基本指令,拥抱Linux的第一步
[Linux]常见指令 Linux基本指令指令的本质ls指令pwd指令cd指令touch指令mkdir指令(重要)rmdir&&rm指令(重要)man指令(重要)cp指令(重要)mv指令(重要)重定向cat指令more指令less指令(重要…...
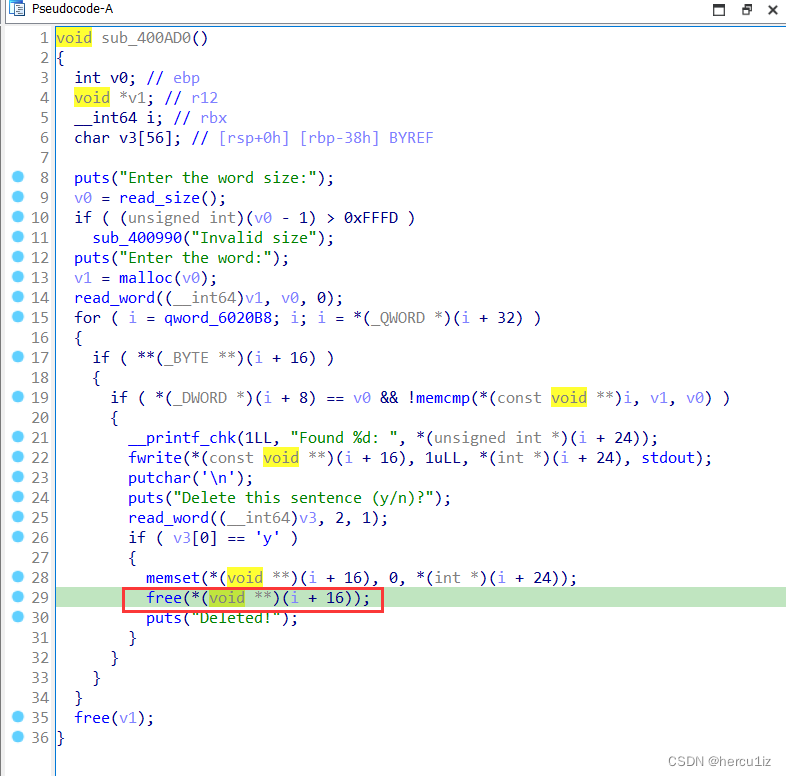
CTF 2015: Search Engine-fastbin_dup_into_stack
参考: [1]https://gsgx.me/posts/9447-ctf-2015-search-engine-writeup/ [2]https://blog.csdn.net/weixin_38419913/article/details/103238963(掌握利用点,省略各种逆向细节) [3]https://bbs.kanxue.com/thread-267876.htm(逆向调试详解&am…...

DRF之全局异常处理
一、REST framework 提供了异常处理,我们可以自定义异常处理函数 使用方式: from rest_framewoork.views import exception_handerdef custom_exception_handler(exc,context):# 先调用REST framework默认的异常处理方法获得标准错误响应对象response …...

AI创作工具的使用体验报告
下面是AI创作工具的使用体验报告,围绕以下三点展开: 一、工具的使用体验如何? CSDN博客AI创作工具是一款非常易用的工具,操作简单,可以很快地开始创建内容。在使用过程中,我发现它的语言模型很智能&#…...
)
C++算法模板(转自acwing)
快速排序算法模板 —— 模板题 AcWing 785. 快速排序 void quick_sort(int q[], int l, int r) {if (l > r) return;int i l - 1, j r 1, x q[l r >> 1];while (i < j){do i ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i],…...
阿里云服务器最新优惠价格及最新收费标准(2023更新)
阿里云服务器收费标准分为包年包月和按量付费两种模式,包年包月是一种先付费后使用的计费方式,按量付费是一种先使用后付费的计费方式。选择包年包月的收费模式,用户可以提前预留资源,同时享受更大的价格优惠,帮您更大…...

React实现监听粘贴事件并获取粘贴板中的截图
目录 监听粘贴事件并获取粘贴板中的截图 TSX中给组件添加监听粘贴事件从粘贴板获取截图文件React监听事件 事件监听绑定的事件函数相关扩展 监听粘贴事件并获取粘贴板中的截图 TSX中给组件添加监听粘贴事件 ? 1 2 3 4 5 6 7 8 9 10 11 const pasteImageRef useRef<HTML…...

ISO_IEC_7816-3
介绍 ISO/IEC 7816 是一系列标准,规定了集成电路卡和此类卡的使用 互换。 这些卡是用于在外部世界和卡中的集成电路之间协商的信息交换的识别卡。 作为信息交换的结果,卡传递信息(计算结果、存储的数据)和/或修改其内容࿰…...
)
学习C#反射(Reflection)
反射提供描述程序集、模块和类型的对象(Type 类型)。 可以使用反射动态地创建类型的实例,将类型绑定到现有对象,或从现有对象中获取类型,然后调用其方法或访问器字段和属性。 如果代码中使用了特性(Attribute)…...

Spring Boot的核心组件和工作原理
引言 Spring Boot是一个快速构建应用程序的框架,通过自动化配置和约定优于配置的原则,可以快速地创建可独立运行的、生产级别的Spring应用程序。Spring Boot的核心组件是自动配置、起步依赖和嵌入式Web服务器。 在本文中,我们将深入了解Spr…...

【指针的深刻理解】
如何看待下面代码中的a变量? #include<stdio.h> int main() {int a 0;//同样的一个a,在不同的表达式中,名称是一样的,但是含义是完全不同的!a 10;//使用的是a的空间:左值int b a; //使用的是a的内容&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
