Day53【动态规划】1143.最长公共子序列、1035.不相交的线、53.最大子序和
1143.最长公共子序列
力扣题目链接/文章讲解
视频讲解
本题最大的难点还是定义 dp 数组
本题和718.最长重复子数组区别在于这里不要求是连续的了,但要有相对顺序
直接动态规划五部曲!
1、确定 dp 数组下标及值含义
dp[i][j]:取 text1 中下标 [0, i - 1] 的子字符串与 text2 中下标为 [0, j - 1] 的子字符串,dp[i][j] 的值表示这两个子字符串的最长公共子序列长度为 dp[i][j]
2、确定递推公式
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1] 不相同
注意不要求连续
- 如果 text1[i - 1] 与 text2[j - 1] 相同,那么找到了一个公共元素,所以 dp[i][j] = dp[i - 1][j - 1] + 1
- 如果 text1[i - 1] 与 text2[j - 1] 不相同,则 text1[0, i - 1] 与 text2[0, j - 1] 的最长公共子序列长度一定为 text1[0, i - 2] 与 text2[0, j - 1] 的最长公共子序列长度或 text1[0, i - 1] 与 text2[0, j - 2] 的最长公共子序列长度之一,取最大的
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
代码如下
if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}3、dp 数组初始化
需要初始化第一列和第一行 dp 数组
先看看 dp[i][0] 应该是多少呢?
test1[0, i-1] 和空串的最长公共子序列自然是 0,所以 dp[i][0] = 0
同理 dp[0][j] 也是 0
其他下标都是随着递推公式逐步覆盖,初始为多少都可以
4、确定遍历顺序
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图
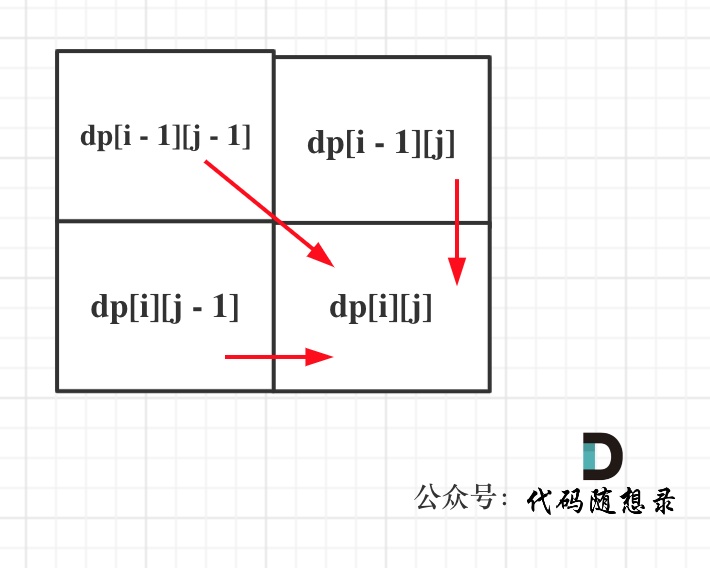
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵
5、打印 dp 数组验证
代码如下
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int> > dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); ++i) {for (int j = 1; j <= text2.size(); ++j) {if (text1[i - 1] == text2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);}}return dp[text1.size()][text2.size()];}
};这里,定义 dp 数组为取 text1 中下标 [0, i - 1] 的子字符串与 text2 中下标为 [0, j - 1] 的子字符串,dp[i][j] 的值表示这两个子字符串的最长公共子序列长度为 dp[i][j]
这里的 i - 1 是为了方便初始化
我们也可以如下定义: 定义 dp 数组为取 text1 中下标 [0, i] 的子字符串与 text2 中下标为 [0, j] 的子字符串,dp[i][j] 的值表示这两个子字符串的最长公共子序列长度为 dp[i][j]
这样我们的代码在初始化部分会复杂一点
代码及注释如下
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {// 1、定义dp数组下标及含义// dp[i][j]表示text1[0, i]与text2[0, j]这两个子串的最长公共子序列的长度vector<vector<int> > dp(text1.size(), vector<int>(text2.size(), 1));// 2、确定递推公式:考虑text1[i]与text2[j]是否相同// 如果相同,则dp[i][j] = dp[i-1][j-1]+1,即text1[0,i-1]与text2[0, j-1]这两子串的最长公共子序列长度+1// 如果不相同,则dp[i][j]一定为text1[0, i-1]与text2[0, j]的最长公共子序列长度或text1[0, i]与text2[0, j-1]的最长公共子序列长度之一,取最大的// 3、dp数组初始化,需要初始化第一行和第一列for (int j = 0; j < text2.size(); ++j) { // 初始化第一行// dp[0][j]表示text1[0]与text2[0, j]的最长公共子序列长度,如果text2[0, j]包含text1[0],则为1,否则为0if (text2[j] == text1[0])break; // 如果遍历到满足条件的了,则当前包括后面的text2[0, j]一定包含text1[0]了,就为1dp[0][j] = 0; // 否则说明当前串text2[0, j]一定不含text1[0]}for (int i = 0; i < text1.size(); ++i) { // 初始化第一列if (text1[i] == text2[0])break;dp[i][0] = 0;}// 4、确定遍历顺序:从前向后从上向下遍历填充for (int i = 1; i < text1.size(); ++i)for (int j = 1; j < text2.size(); ++j)if (text1[i] == text2[j])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);// 5、打印dp数组验证return dp[text1.size() - 1][text2.size() - 1];}
};1035.不相交的线
力扣题目链接/文章讲解
视频讲解
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度
和上一道题一模一样
直接上代码
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {// dp[i][j]表示nums1[0, i]与nums2[0, j]这两个子数组的最长公共子序列的长度vector<vector<int> > dp(nums1.size(), vector<int>(nums2.size(), 1));for (int j = 0; j < nums2.size(); ++j) {if (nums2[j] == nums1[0]) break;dp[0][j] = 0;}for (int i = 0; i < nums1.size(); ++i) {if (nums1[i] == nums2[0]) break;dp[i][0] = 0;}for (int i = 1; i < nums1.size(); ++i)for (int j = 1; j < nums2.size(); ++j) {if (nums1[i] == nums2[j])dp[i][j] = dp[i-1][j-1] + 1;elsedp[i][j] = max(dp[i-1][j], dp[i][j-1]);}return dp[nums1.size()-1][nums2.size()-1];}
};53.最大子数组和
力扣题目链接/文章讲解
视频讲解
本题可以用贪心算法,也可以用动态规划
1、确定 dp 数组下标及值含义
dp[i]:下标 i 表示以 nums[i] 为结尾的有最大和的连续子数组,值表示该子数组和
注意 nums[i] 一定是有着最大和的连续子数组中的最后一个元素
2、确定递推公式
dp[i] 只有两个方向可以推出来:
- dp[i - 1] + nums[i],即:nums[i] 加入当前以 nums[i-1] 为结尾的连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i])
3、dp 数组初始化
从递推公式可以看出来 dp[i] 是依赖于 dp[i - 1] 的状态,dp[0] 就是递推公式的基础
根据 dp 下标及值含义:dp[0] = nums[0]
4、确定遍历顺序
递推公式中 dp[i] 依赖于 dp[i - 1] 的状态,需要从前向后遍历,保证被依赖的 dp 值是已被更新后的正确值
5、打印 dp 数组验证
代码如下
class Solution {
public:int maxSubArray(vector<int>& nums) {// 确定dp数组下标及值含义:i表示以nums[i]为结尾的有最大和的子数组,dp[i]的值表示该最大子数组和vector<int> dp(nums.size());// 递推公式:要么将nums[i]加入具有最大和的子数组,要么从nums[i]重新开始统计具有最大和的子数组// 初始化dp[0]dp[0] = nums[0];// 从左向右遍历填充dpfor (int i = 1; i < nums.size(); ++i)dp[i] = max(dp[i - 1] + nums[i], nums[i]);return *max_element(dp.begin(), dp.end());}
};回顾一下 dp[i] 的定义:下标 i 表示以 nums[i] 为结尾的有最大和的连续子数组
那么我们要找有最大和的子数组,就应该找每一个 nums[i] 为终点的有最大和的子数组
回顾总结
操作两个序列需要二维 dp
还是定义 dp 数组是关键
相关文章:

Day53【动态规划】1143.最长公共子序列、1035.不相交的线、53.最大子序和
1143.最长公共子序列 力扣题目链接/文章讲解 视频讲解 本题最大的难点还是定义 dp 数组 本题和718.最长重复子数组区别在于这里不要求是连续的了,但要有相对顺序 直接动态规划五部曲! 1、确定 dp 数组下标及值含义 dp[i][j]:取 text1…...

Three.js--》实现3d地球模型展示
目录 项目搭建 实现网页简单布局 初始化three.js基础代码 创建环境背景 加载地球模型 实现光柱效果 添加月球模型 今天简单实现一个three.js的小Demo,加强自己对three知识的掌握与学习,只有在项目中才能灵活将所学知识运用起来,话不多…...
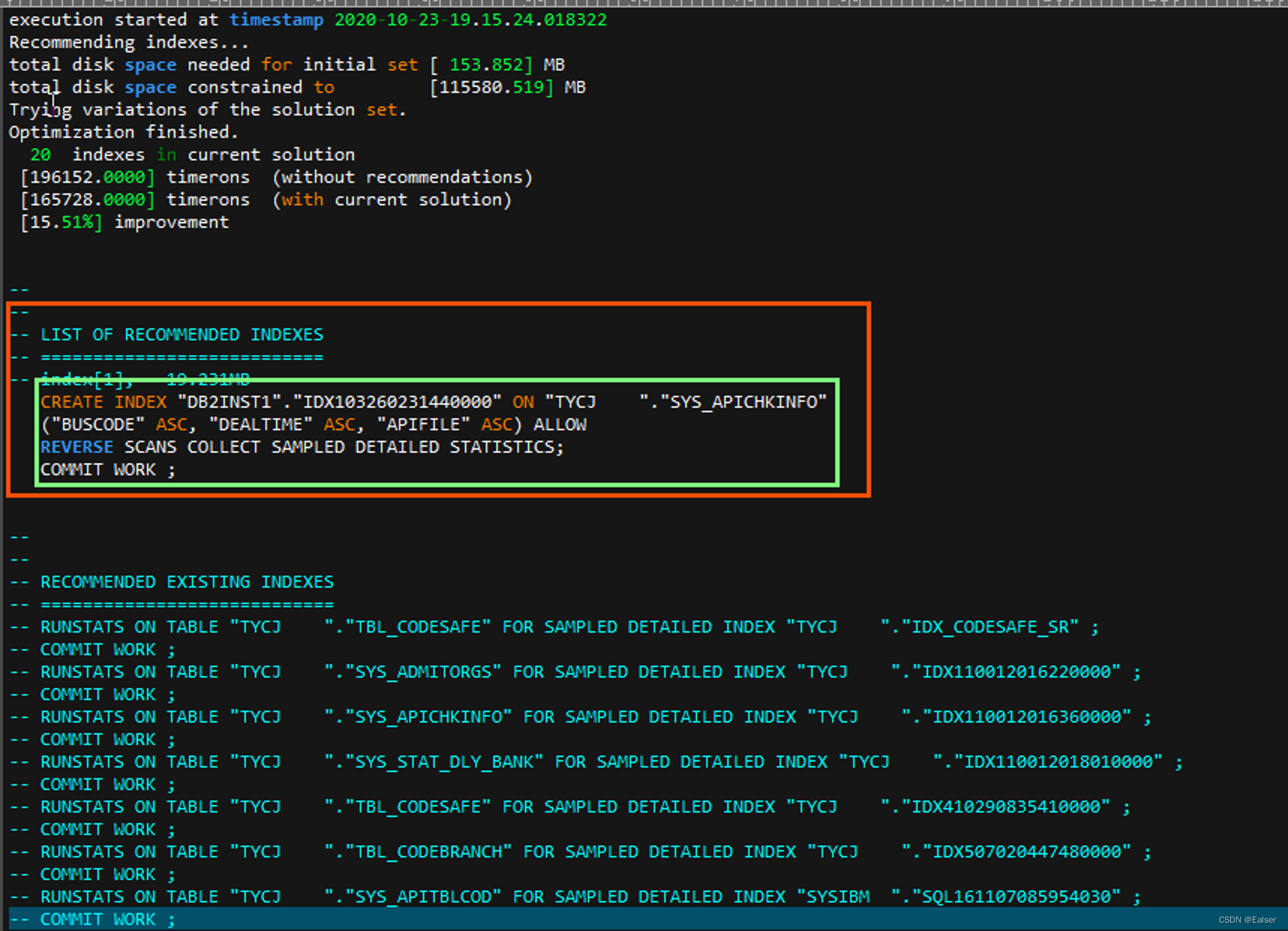
<SQL>《SQL命令(含例句)精心整理版(6)》
《SQL命令(含例句)精心整理版(6)》 18 DB2查询语句18.1 查询数据库大小18.2 查看表占表空间大小18.3 查看正在执行的语句18.4 db2expln 查看执行计划18.5 db2advis 查看优化建议 19 空值19.1 NULL19.2 TRIM 18 DB2查询语句 18.1 …...
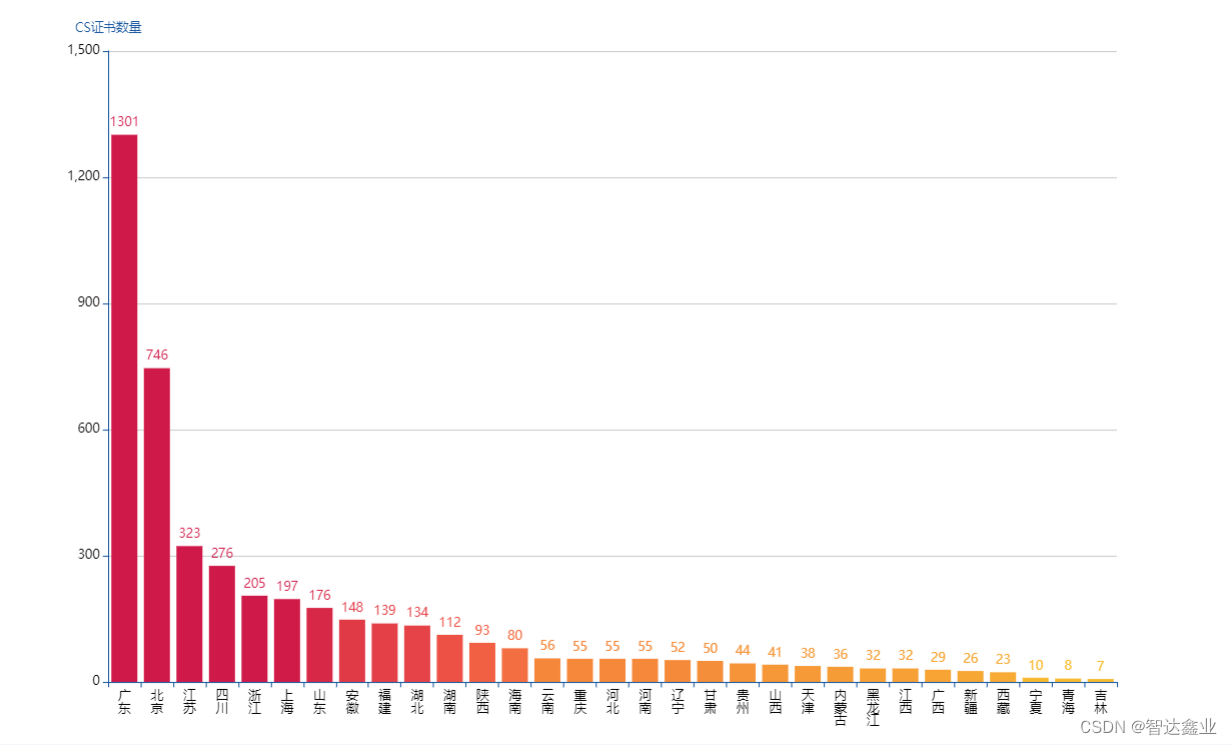
信息系统建设和服务能力评估证书CS
信息系统建设和服务能力评估体系CS简介 简介:本标准(团标T/CITIF 001-2019)是信息系统建设和服务能力评估体系系列标准的第一个,提出了对信息系统建设和服务提供者的综合能力要求。 发证单位:中国电子信息行业联合会。…...

vue3引入路由
1.首先在项目中安装路由 npm install vue-router -S 2.src文件夹下新建》views文件夹》新建home文件夹》新建Home.vue文件 在src文件夹下》新建router文件夹》新建index.js import { createRouter,createWebHashHistory } from vue-router const route s[ { path:/, compo…...
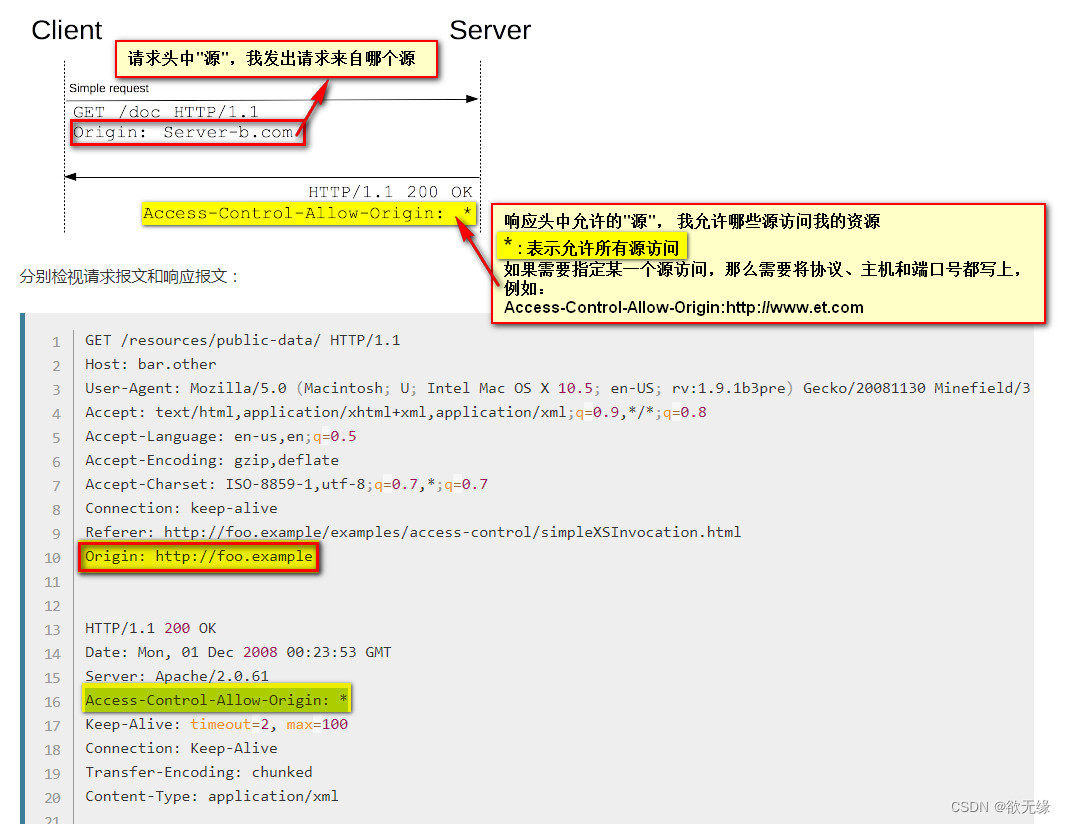
前后端联调跨域问题
文章目录 什么是同源策略如何判断是否同源?跨域资源共享(CORS)如何解决跨域问题 什么是同源策略 同源策略限制了从同一个源加载的文档或脚本如何与来自另一个源的资源进行交互。这是一个用于隔离潜在恶意文件的重要安全机制。 如何判断是否同源? 如果…...
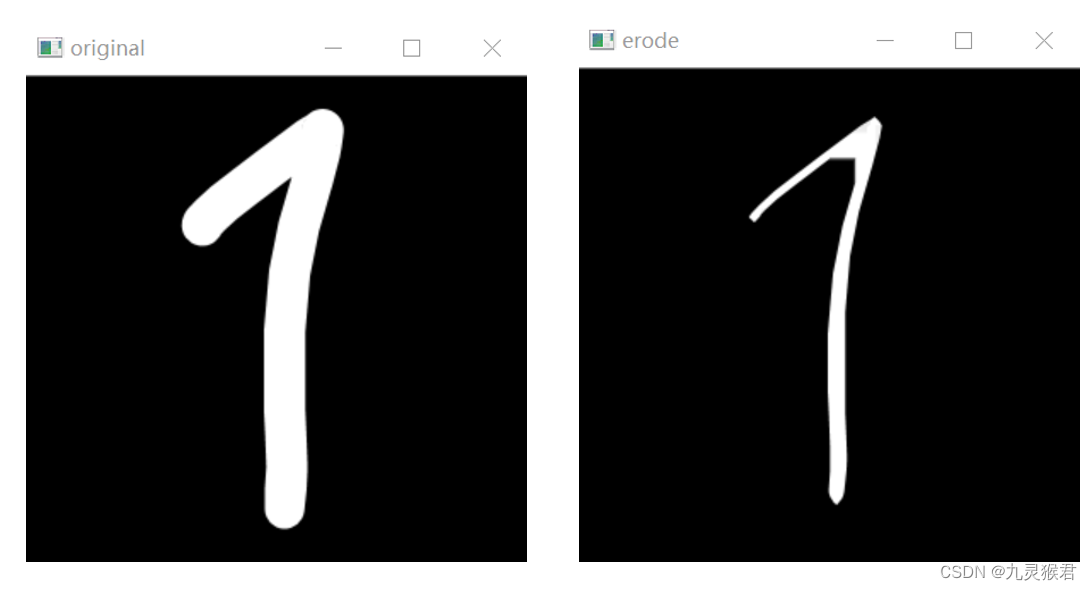
day11 - 手写数字笔迹细化
手写数字笔迹细化 对于手写数字识别实验中,经常会遇到因为笔迹较粗导致误识别的情况,所以我们通常会先将笔迹进行细化,笔迹变细以后,数字的特征会更明显,后续进行识别的准确率就会更高。 例如数字7 和 1 ,…...

C++ QT QDBus基操
以下是使用QDBus进行跨进程通信的具体用法: 1. 创建DBus服务 在服务端进程中,需要创建一个DBus服务,并注册DBus对象。示例代码如下: #include <QDBusConnection> #include <QDBusMessage> #include <QDBusInterf…...
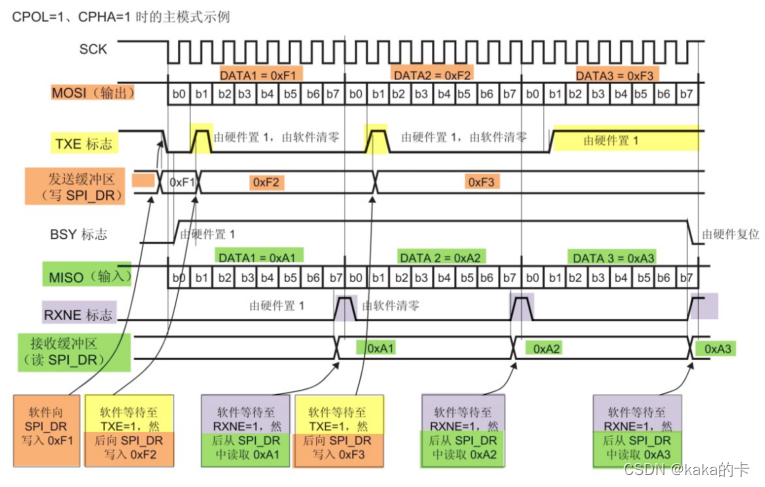
STM32的SPI外设
文章目录 1. STM32 的 SPI 外设简介2. STM32 的 SPI 架构剖析2.1 通讯引脚2.2 时钟控制逻辑2.3 数据控制逻辑2.4 整体控制逻辑 3. 通讯过程4. SPI 初始化结构体详解 1. STM32 的 SPI 外设简介 STM32 的 SPI 外设可用作通讯的主机及从机,支持最高的 SCK 时钟频率为 …...

VMWare ESXI6.7创建虚拟机
VMware ESXi:专门构建的裸机 管理程序 首先开启ESXI主机 登录ESXI 打开浏览器输入物理机ip,输入账号密码进行登录 创建虚拟机 选择创建类型 创建RedHat7.6 选择存储类型和数据存储 仅一个存储,直接点下一页即可 配置虚拟机硬件和虚拟机附…...
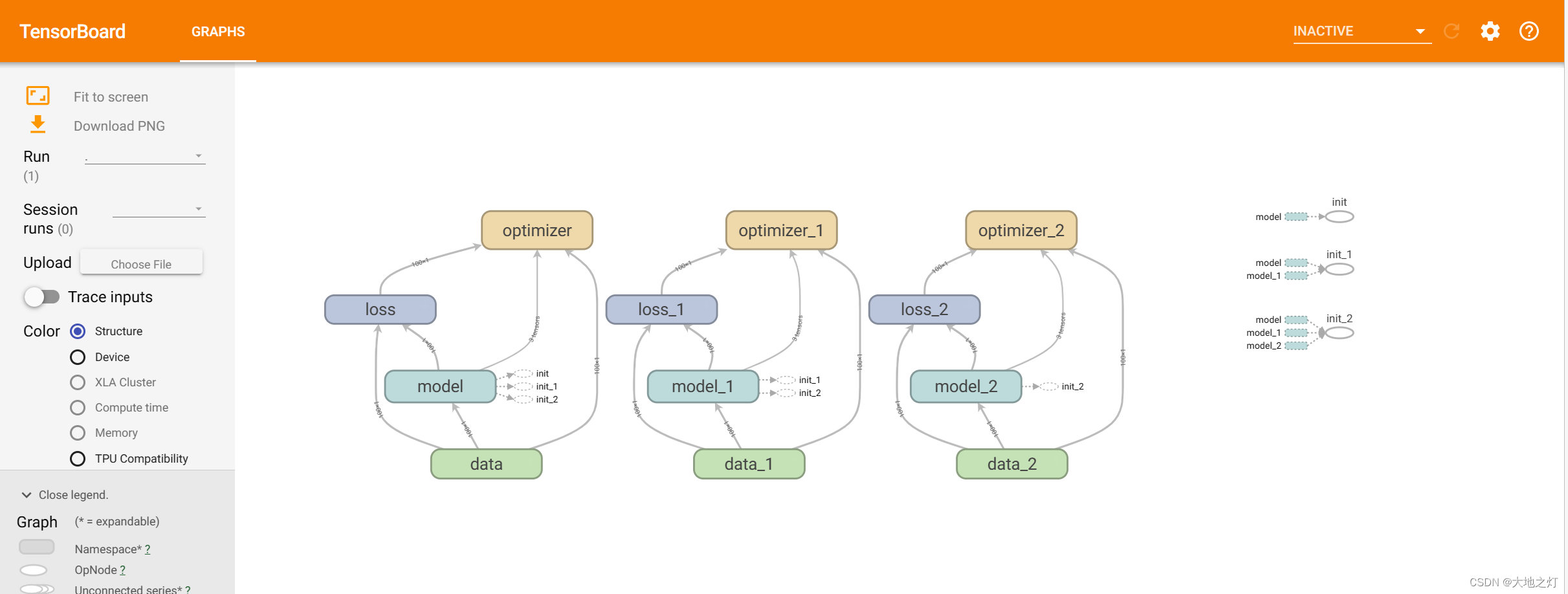
TensorFlow 1.x学习(系列二 :4):自实现线性回归
目录 线性回归基本介绍常用的op自实现线性回归预测tensorflow 变量作用域模型的保存和加载 线性回归基本介绍 线性回归: w 1 ∗ x 1 w 2 ∗ x 2 w 3 ∗ x 3 . . . w n ∗ x n b i a s w_1 * x_1 w_2 * x_2 w_3 * x_3 ... w_n * x_n bias w1∗x1w2∗…...

Openwrt折腾记6-网络摄像头
前言: 前几天买了个电视机上的摄像头,但是估计是电视配置或软件不好,视频通话太卡顿。今天把它装的极路由4的usb上了。由于当初挑的是电视免驱的,所以我猜想是通用的芯片。 调查驱动 LINUX uvc支持型号的列表里 http://www.ide…...
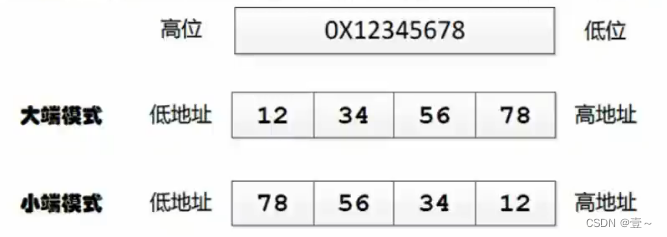
C++判断大端小端
C判断大端小端 1. 基础知识 大端小端其实表示的是数据在存储器中的存放顺序。 大端模式:数据的高字节存放在内存的低地址中,而低字节则存放在高地址中。地址由小到大增加,数据则从高位向低位存放,这种存放方式符合人类的正常思维…...

K8S RBAC之Kubeconfig设置用户权限,不同的用户访问不同的namespace
1.CA签发客户端证书 检查证书是否存在 # ll /etc/kubernetes/pki/ 总用量 48K -rw-r----- 1 kube root 2.1K 3月 2 16:44 apiserver.crt -rw------- 1 kube root 1.7K 3月 2 16:44 apiserver.key -rw-r----- 1 kube root 1.2K 3月 2 16:44 apiserver-kubelet-client.cr…...
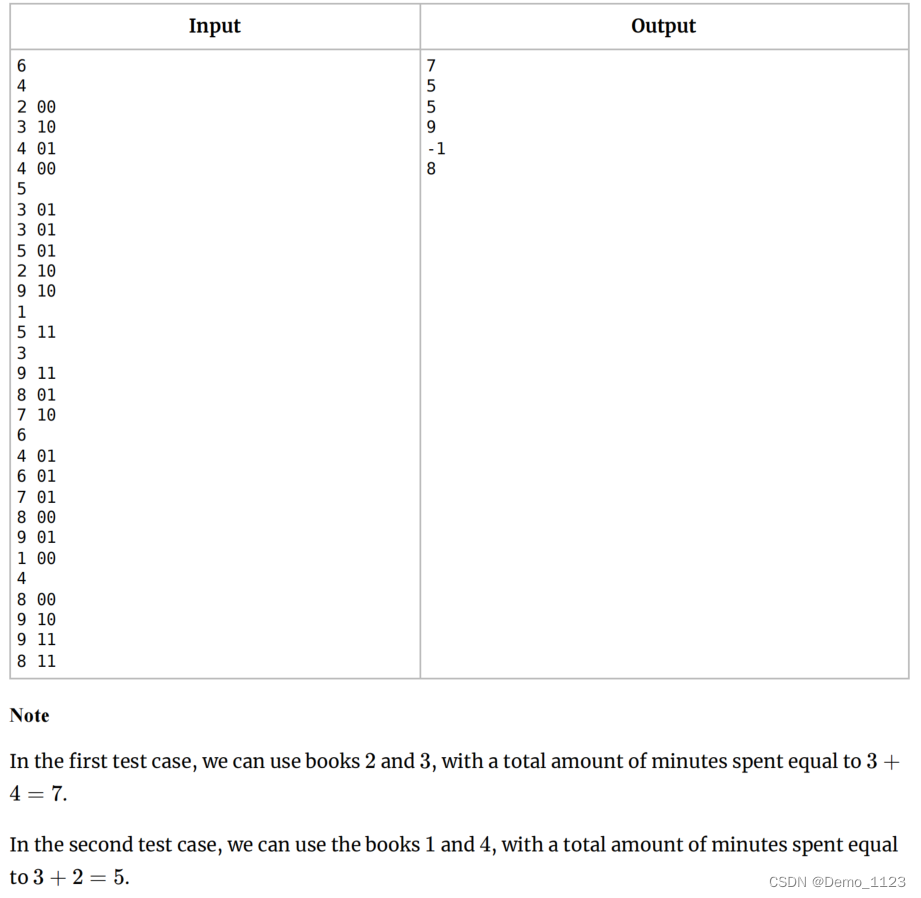
CodeForces..学习读书吧.[简单].[条件判断].[找最小值]
题目描述: 题目解读: 给定一组数,分别是 “时间 内容”,内容分为00,01,10,11四种,求能够得到11的最小时间。 解题思路: 看似00,01,10࿰…...

灵活使用Postman环境变量和全局变量,提高接口测试效率!
目录 前言: 环境变量和全局变量的概念 环境变量和全局变量的使用方法 1. 定义变量 2. 使用变量 环境变量和全局变量的实例代码 变量的继承和覆盖 变量的动态设置 总结: 前言: Postman是一个流行的API开发和接口测试工具,…...

Springboot+Vue3 整合海康获取视频流并展示
目录 1.后端 1.1 导入依赖 1.2 代码实战 2.前端 2.1 首先安装海康的web插件,前端vue3代码如下: 1.后端 1.1 导入依赖 <dependency><groupId>com.hikvision.ga</groupId><artifactId>artemis-http-client</artifactId&g…...
Linux——进程退出
目录 一.进程退出时有三种选择: 1.1 echo $?命令: 功能: 打印距离现在最近一次执行某进程的退出码 例2代码: 例3: 例4代码: 1.3 进程运行过程中可能会出现的错误种类: 二.总结ÿ…...

组长给组员派活,把组长自己的需求和要改的bug派给组员,合理吗?
组长把自己的工作派给手下,合理吗? 一位程序员问: 组长给他派活,把组长自己的需求或者要改的bug派给他。组长分派完需求之后,他一个人干两个项目,组长却无所事事,这样合理吗? 有人说…...

Spring注解开发——bean的作用范围与生命周期管理
文章目录 1.bean管理1.1 bean作用范围Scope注解 1.2 bean生命周期PostConstructPreDestroy 2.小结 1.bean管理 1.1 bean作用范围 Scope注解 不写或者添加Scope(“singleton”)表示的是单例 如何配置多例? 在Scope(“prototype”)表示的是多例 1.2 bean生命周…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
