单调队列优化dp
文章目录
- 单调队列优化dp
- 烽火传递
- 修剪草坪
- 绿色通道
- 琪露诺
- 旅行问题
- Watching Fireworks is Fun
- 瑰丽华尔兹
- 股票交易
单调队列优化dp
文章首发于我的个人博客:欢迎大佬们来逛逛
单调队列优化dp的建模形式:这是窗口右滑动的情况
对于窗口左滑动的也是同理。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6b43a5LW-1685532776854)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ce3nZm5j-1685532776854)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%201.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cDlxFfpM-1685532776855)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%202.png)]
烽火传递
题目大意:有n个烽火台,在连续的k个烽火台中,至少要有一个发出信号;烽火台发出信号需要消耗代价,问你要使得满足对于所有的烽火台满足条件,最小的代价是多少。
例如:烽火台及其代价如下所示:
1 2 5 6 2 ,其中k=3
我们必须选择两个:
- 1 和 5:代价为6
- 1 和 6:代价为7
- ……
- 2 和 2:代价为4,可以得知这是最优解。
因此我们定义 d p [ i ] dp[i] dp[i] 数组 表示当前位置的最小代价值,因此最后的结果就是 d p [ n ] dp[n] dp[n]
其中状态转移可以由前一些位置的最小的值来转移得到:
d p [ i ] = m i n ( d p [ j ] ) + w [ i ] dp[i]=min(dp[j])+w[i] dp[i]=min(dp[j])+w[i]
其中 d p [ j ] dp[j] dp[j] 中的 j 的位置我们可以根据 k k k 的值来确定:
j ∈ [ i − k , i − 1 ] j \in \left [i-k,i-1 \right ] j∈[i−k,i−1]
这意味如果我们点燃位置为 i i i 的烽火台,则必须满足在 [ i − k , i − 1 ] \left [i-k,i-1 \right ] [i−k,i−1] 位置至少点燃一个烽火台:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EiRqpji2-1685532776855)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%203.png)]
因此我们枚举 i i i 的位置,对于每一个位置通过单调队列维护前面区间内一个最小值,然后根据上面的状态转移方程转移即可。
本题的单调队列的滑动窗口范围是往右滑动的
#include<bits/stdc++.h>
#if 0#define int long long
#endifconst int N=1e6+10;
int n,k;
int w[N],dp[N];
std::deque<int> deq;
signed main(){ std::cin>>n>>k;for (int i=1;i<=n;i++){std::cin>>w[i];} int ans=1e9;for (int i=1;i<=n;i++){if (!deq.empty() && deq.front()<i-k){deq.pop_front();}//维护队列最小值while (!deq.empty() && dp[i-1]<=dp[deq.back()]){deq.pop_back();}deq.push_back(i-1);dp[i]=dp[deq.front()]+w[i];if (i>=n-k+1){ans=std::min(ans,dp[i]);}}std::cout<<ans;return 0;
}
修剪草坪
题目大意:在数列中选出长度不超过k的子序列,然后得到每个子序列的和,计算和的最大值,其中元素不能重复选择。
示例给出了:
1 2 3 4 5 ,其中k=2
最优解是选择1 2 和 4 5两个子序列,结果为 12
根据贪心的思想,如果我们想要使得最后的和最大, 应该尽量往长了选,则我们假设选择了n个长度为 k 的子序列,则第 k+1 个数字一定不会选,因此我们就可以对这个不会选的数字进行操作。
与其让我们求n个 长度为k 的子序列的和的最大值,不如求在 n个 长度为k+1 的子序列中选择最小值,然后计算他们的和,最后直接用整个数列的和减去由若干最小值组成的和即可。
因此状态转移方程如下:
d p [ i ] = m i n ( d p [ j ] ) + w [ i ] dp[i]=min(dp[j]) +w[i] dp[i]=min(dp[j])+w[i]
注意 d p dp dp 数组表示的是在 k+1 长度中选择的最小值。
其中 j j j 的取值范围是:
j ∈ [ i − k , i − 1 ] j \in \left [i-k,i-1 \right ] j∈[i−k,i−1]
本题的单调队列的滑动窗口范围是往右滑动的
#include<bits/stdc++.h>
#if 1#define int long long
#endifconst int N=1e6+10;
int n,k;
int w[N],dp[N];
std::deque<int> deq;
signed main(){ std::cin>>n>>k;for (int i=1;i<=n;i++){std::cin>>w[i];} k+=1;//选择子序列,并且使得数列中没有连续的超过k个数被选,使得选择的数之和最大//选择不超过连续k个数字之和的最大值 ==> sum-选择k+1个数字组成若干个最小值int sum=1e18;for (int i=1;i<=n;i++){if (!deq.empty() && deq.front()<i-k){deq.pop_front();}while (!deq.empty() && dp[deq.back()]>=dp[i-1]){deq.pop_back();}deq.push_back(i-1);dp[i]=dp[deq.front()]+w[i];if (i>=n-k+1){//获得最小值sum=std::min(sum,dp[i]);}}std::cout<<std::accumulate(w+1,w+1+n,0ll)-sum;return 0;
}
绿色通道
绿色通道 - 洛谷
题目大意:在规定的时间内做一定数量的题目,做一道题目需要消耗一定的时间。最后使得未做的最长的空题目段的长度最小值,求这个最小值。
根据题目描述的最大值最小,我们很容易想到是二分答案
同时题目告诉你了最长的空题目段越长,马老师越生气,这就是相当于满足了单调性。
因此我们可以二分查找 空题目段的长度,然后选择套用二分查找求最小值的模板即可。
其中我们在二分查找的过程中,假设当前的空题目段长度为 k, 则第 k+1 题目一定不是,因此我们就可以像上一道题目那样,单调队列维护区间最小值。
注意到我们二分的是 k+1 的长度,因此最后我们还需要 -1
#include<bits/stdc++.h>
#if 1#define int long long
#endifconst int N=5e4+10;
int dp[N],w[N];
int n,t;
bool check(int mid){//mid表示选择的空题目段长+1 std::deque<int> deq;memset(dp,0,sizeof(dp));for (int i=1;i<=n;i++){if (!deq.empty() && deq.front()<i-mid){deq.pop_front();}while (!deq.empty() && dp[deq.back()]>=dp[i-1]){deq.pop_back();}deq.push_back(i-1);dp[i]=dp[deq.front()]+w[i];if (i>=n-mid+1 && dp[i]<=t){//mid越大,表示选择的空题目段越长,则能做的题目就越少,因此不超过t分钟的条件就越容易满足,此时返回true,更新最小值return true;}}return false;
}
signed main(){std::cin>>n>>t;for (int i=1;i<=n;i++){std::cin>>w[i];}//最大值最小:使得最长的空题段最短是多少//二分选择的 空题段长+1int l=-1,r=n+1;while (l+1<r){int mid=l+r>>1;if (check(mid)){r=mid;}else{l=mid;}}std::cout<<r-1;return 0;
}
琪露诺
琪露诺 - 洛谷
题目大意:每次可以走 [ x + L , x + R ] \left [x+L,x+R \right ] [x+L,x+R] 中的任意一个位置,同时每个位置具有一个值,最后使得走完这 n 个点之后 能够获得的最大值是多少。
很容易可以看出来这道题目是给定区间的单调队列优化 的问题。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8gykVs2O-1685532776856)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%204.png)]
状态转移方程与前面都是一样的。
#include<bits/stdc++.h>
#if 0#define int long long
#endif
const int N=2e5+10;
int n,l,r;
int w[N],dp[N];
std::deque<int> deq;
signed main(){std::cin>>n>>l>>r;for (int i=0;i<=n+1;i++){std::cin>>w[i];}//i可以跳跃到[i+l,i+r]中的任意位置//同理i位置可以由[i-r,i-l]区间中任意位置跳跃过来,维护窗口中的最大值即可memset(dp,-0x3f,sizeof(dp));dp[0]=0;int ans=-1e9;//注意从l开始,因为一开始只能跳到[l,r]的位置for (int i=l;i<=n;i++){if (!deq.empty() && deq.front()<i-r){deq.pop_front();}//维护单调队列最大值while (!deq.empty() && dp[deq.back()]<=dp[i-l]){deq.pop_back();}deq.push_back(i-l);dp[i]=dp[deq.front()]+w[i];if (i>=n-r+1){ans=std::max(ans,dp[i]); //在最后的区间内累加答案}}std::cout<<ans;return 0;
}
旅行问题
题目大意:n个车站组成一个环,在每个车站有加油量和到下一站的距离,问你从任意的车站出发能够到达最后的终点,即绕一圈。
我们定义 s u m [ i ] sum[i] sum[i] 表示为从 i 号车站出发到下一站剩余的流量:
s u m [ i ] = s u m [ i + n ] = o i l [ i ] − d i s [ i ] sum[i] = sum[i+n] =oil[i] -dis[i] sum[i]=sum[i+n]=oil[i]−dis[i]
对于环形的问题,我们常常断环成链。
然后计算他们的前缀和:
s u m [ i ] + = s u m [ i − 1 ] sum[i] +=sum[i-1] sum[i]+=sum[i−1]
对于判断 i 号点能否绕一圈,我们可以用
s u m [ j ] − s u m [ i − 1 ] > = 0 sum[j]-sum[i-1]>=0 sum[j]−sum[i−1]>=0
来判断,如果此值大于等于0,则说明 i 号点可以绕一圈,对于 j 我们可以单调队列维护一个最小的 j
同时判断逆时针能够绕一圈,我们可以维护一个后缀和,然后执行相反的操作即可:
s u m [ j ] − s u m [ i + 1 ] > = 0 sum[j]-sum[i+1]>=0 sum[j]−sum[i+1]>=0
此题我们需要同时维护往左滑动的窗口,代表顺时针;和一个维护往右滑动的窗口,代表逆时针。
#include<bits/stdc++.h>
#if 1#define int long long
#endifconst int N=1e6+10;
int n;
int oil[N],dis[N];
int sum[N<<2],fg[N<<2]; //sum[i]表示从i点出发顺时针或者逆时针到达各个点的剩余油量
std::deque<int> deq;
signed main(){std::cin>>n;for (int i=1;i<=n;i++){std::cin>>oil[i]>>dis[i];}//顺时针for (int i=1;i<=n;i++){sum[i]=sum[i+n]=oil[i]-dis[i];}for (int i=1;i<=n*2;i++){sum[i]+=sum[i-1];}//窗口往左滑动for (int i=n*2;i>=1;i--){if (!deq.empty() && deq.front()>i+n-1){deq.pop_front();}//维护最小的sum[j],如果sum[j]-sum[i-1]=0则满足i点可以绕一圈while (!deq.empty() && sum[deq.back()]>=sum[i]){deq.pop_back();}deq.push_back(i);if (i<=n && sum[deq.front()]-sum[i-1]>=0){fg[i]=true;}}memset(sum,0,sizeof(sum));deq.clear();//逆时针dis[0]=dis[n];for (int i=n;i>=1;i--){sum[i]=sum[i+n]=oil[i]-dis[i-1];}for (int i=n*2;i>=1;i--){sum[i]+=sum[i+1];}//窗口往右边滑动for (int i=1;i<=n*2;i++){if (!deq.empty() && deq.front()<i-n+1){deq.pop_front();}while (!deq.empty() && sum[deq.back()]>=sum[i]){deq.pop_back();}deq.push_back(i);if (i>=n+1 && sum[deq.front()]-sum[i+1]>=0){//注意此时的序号为i-nfg[i-n]=true;}}for (int i=1;i<=n;i++){if (fg[i]){std::cout<<"TAK\n";}else{std::cout<<"NIE\n";}}return 0;
}
Watching Fireworks is Fun
Watching Fireworks is Fun - 洛谷
题目大意:通过移动位置x使得 b i − ∣ a i − x ∣ b_i - |a_i-x| bi−∣ai−x∣ 来获得最大值
注意到从一个位置到另一个位置可以通过两种方式得到:
窗口向右滑动:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zvmx4IpO-1685532776856)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%205.png)]
窗口向左滑动:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eeg75d6t-1685532776857)(%E5%8D%95%E8%B0%83%E9%98%9F%E5%88%97%E4%BC%98%E5%8C%96dp%20dd9f82e1dca24b29ac9925e1303dfacb/Untitled%206.png)]
我们定义 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示当前放的是第 i 次烟花,位置为 j 时的最大权值。
状态转移方程如下:
d p [ n o w ] [ i ] = d p [ p r e ] [ j ] + b [ i ] − a b s ( a [ i ] − x ) dp[now][i]=dp[pre][j]+ b[i]-abs(a[i]-x) dp[now][i]=dp[pre][j]+b[i]−abs(a[i]−x)
可以利用滚动数组优化,把数组将为二维。
#include<bits/stdc++.h>
#if 1#define int long long
#endifconst int N=150010;
int dp[2][N]; //滚动数组: dp[i][j]表示放第i个烟花,当前位置位于j时的最大快乐值
int n,m,d;
int a[N],b[N],t[N];
signed main(){std::cin>>n>>m>>d;for (int i=1;i<=m;i++){std::cin>>a[i]>>b[i]>>t[i];}memset(dp,-0x3f,sizeof(dp));for (int i=1;i<=n;i++){dp[0][i]=0; //初始化,放第0个烟花,位置在任何时刻都是0快乐度}//遍历烟花for (int z=1;z<=m;z++){//now表示当前,pre表示上一个int now=z&1,pre=(z-1)&1;std::deque<int> deq;//遍历位置:窗口往右滑动for (int i=1;i<=n;i++){if (!deq.empty() && deq.front()<i-d*(t[z]-t[z-1])){deq.pop_front();}//维护队列最大值while (!deq.empty() && dp[pre][deq.back()]<=dp[pre][i]){deq.pop_back();}deq.push_back(i);dp[now][i]=dp[pre][deq.front()]+b[z]-abs(a[z]-i);}//窗口往左滑动for (int i=n;i>=1;i--){if (!deq.empty() && deq.front()>i+d*(t[z]-t[z-1])){deq.pop_front();}while (!deq.empty() && dp[pre][deq.back()]<=dp[pre][i]){deq.pop_back();}deq.push_back(i);dp[now][i]=std::max(dp[now][i],dp[pre][deq.front()]+b[z]-abs(a[z]-i));}}int ans=-1e18;//最后一次在m&1,位置为j时枚举一个最大值for (int i=1;i<=n;i++){ans=std::max(dp[m&1][i],ans);}std::cout<<ans;return 0;
}
瑰丽华尔兹
[NOI2005] 瑰丽华尔兹 - 洛谷
题目大意:往上下左右四个方向移动,每次都可以选择移动或者停止,求最后的最大移动路程
设 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示当前位置为 ( i , j ) (i,j) (i,j) 时的最大移动距离。
我们首先需要枚举四个方向,然后进行求解。
我们先来看往右移动的话:
很容易想到状态转移方程:
d p [ i ] [ j ] = m a x ( d p [ i ] [ k ] + j − k ) dp[i][j]=max(dp[i][k]+j-k) dp[i][j]=max(dp[i][k]+j−k)
即当前点的最大移动距离就等于 ( i , k ) (i,k) (i,k) 点的距离 + ( j − k ) (j-k ) (j−k) 的距离。
因此我们只需要维护一个 d p [ i ] [ k ] + j − k dp[i][k] +j-k dp[i][k]+j−k 的最大值,我们可以使用单调队列进行维护。
这是向右移动的情况,再考虑其他三种情况也是同样的道理。
但是发现一个问题,往右移动, i 是不变的,但是往下移动的时候,j 又是不变的,我们很难用 d p [ i ] [ k ] dp[i][k] dp[i][k] 来具体的表示四个方向,因此我们抽象为:
d p [ i ] [ j ] = m a x ( f + j − p o s ) dp[i][j]=max(f+j-pos) dp[i][j]=max(f+j−pos)
其中 f f f 就是转移之前的最大移动距离, p o s pos pos 表示的就是转移之前的那个位置。
因此我们对于四种方向的枚举就可以实现了:
for (int i=1;i<=k;i++){int s,t,d; //时间区间[s,t] d方向 1234 上下左右std::cin>>s>>t>>d; int time=t-s+1;if (d==1){//上for (int i=1;i<=m;i++){get(n,i,n,time,d);}}if (d==2){//下for (int i=1;i<=m;i++){get(1,i,n,time,d);}}if (d==3){//左for (int i=1;i<=n;i++){get(i,m,m,time,d);}}if (d==4){//右for (int i=1;i<=n;i++){get(i,1,m,time,d);}}}
其中 g e t get get 函数就是我们维护单个方向滑动窗口最大值的函数:
- x和y:每个方向的起始位置
- L:表示最多在这个方向移动L距离
- time:表示时间间隔。
- d:表示方向,用于移动。
void get(int x,int y,int L,int time,int d);
我们在此函数中利用滑动窗口维护一个最大值即可,注意当碰到障碍的时候,我们的窗口清零。
#include<bits/stdc++.h>
#if 0#define int long long
#endifconst int N=210;
int n,m,x,y,k,ans;
char map[N][N];
int dp[N][N]; //dp[i][j]表示在(i,j)位置的最大价值
int dx[5]{0,-1,1,0,0},dy[5]{0,0,0,-1,1};
struct Node{int pos,dp; //位置和最长距离
};
void get(int x,int y,int L,int time,int d){//(x,y)表示起始位置,L表示当前方向最长移动长度,time表示时间长度std::deque<Node> deq;//注意!!! 这个地方要从(x,y)开始,所有一开始不能把x+=,y+=放在下面,因此要放在for循环的后面for (int i=1;i<=L;i++,x+=dx[d],y+=dy[d]){ //朝着方向d一直移动if (map[x][y]=='x'){deq.clear();}else{//单调队列维护最大值if (!deq.empty() && deq.front().pos<i-time){deq.pop_front();}//维护窗口最大值while (!deq.empty() && deq.back().dp+i-deq.back().pos<=dp[x][y]){deq.pop_back();}deq.push_back({i,dp[x][y]});dp[x][y]=deq.front().dp+i-deq.front().pos;ans=std::max(ans,dp[x][y]);}}
}
signed main(){std::cin>>n>>m>>x>>y>>k;for (int i=1;i<=n;i++){for (int j=1;j<=m;j++){std::cin>>map[i][j];}}memset(dp,-0x3f,sizeof(dp));dp[x][y]=0;for (int i=1;i<=k;i++){int s,t,d; //时间区间[s,t] d方向 1234 上下左右std::cin>>s>>t>>d; int time=t-s+1;if (d==1){//上for (int i=1;i<=m;i++){get(n,i,n,time,d);}}if (d==2){//下for (int i=1;i<=m;i++){get(1,i,n,time,d);}}if (d==3){//左for (int i=1;i<=n;i++){get(i,m,m,time,d);}}if (d==4){//右for (int i=1;i<=n;i++){get(i,1,m,time,d);}}}std::cout<<ans;return 0;
}
股票交易
[SCOI2010]股票交易 - 洛谷
题目大意:在某天可以选择买入股票,卖出股票,其中买入和卖出都有数量限制,并且也具有最大持股数限制,并且还具有时间间隔限制,求得最后能获得的最大利润。
定义 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示第 i i i 天持股 j j j 数量的最大利润。
我们可以分成四种情况讨论:
- 只买入: d p [ i ] [ j ] = − a s ⋅ j dp[i][j]=-as\cdot j dp[i][j]=−as⋅j
- 不买不卖: d p [ i ] [ j ] = m a x ( d p [ i ] [ j ] , d p [ i − 1 ] [ j ] ) dp[i][j]=max(dp[i][j],dp[i-1][j]) dp[i][j]=max(dp[i][j],dp[i−1][j])
- 在之前某天的基础上买入: d p [ i ] [ j ] = m a x ( d p [ i − w − 1 ] [ k ] − a p ∗ ( j − k ) ) dp[i][j]=max(dp[i-w-1][k]-ap*(j-k)) dp[i][j]=max(dp[i−w−1][k]−ap∗(j−k))
- 其中 k k k 的取值范围: k ∈ [ j − a s , j ] k\in [j-as,j] k∈[j−as,j] 表示全买或者一个都不买
- 在之前某天的基础上卖出: d p [ i ] [ j ] = m a x ( d p [ i − w − 1 ] [ k ] + b p ∗ ( k − j ) ) dp[i][j]=max(dp[i-w-1][k]+bp*(k-j)) dp[i][j]=max(dp[i−w−1][k]+bp∗(k−j))
- 其中 k k k 的取值范围: k ∈ [ j , j + b s ] k \in [j,j+bs] k∈[j,j+bs] 表示一个都不卖或者全卖
因此我们便可以使用单调队列维护窗口的最大值了。
其中 k k k 便是我们需要维护的值。
注意窗口的移动情况:
- 买入:窗口往右滑,顺序遍历
- 卖出:窗口往左滑,逆序遍历
#include<bits/stdc++.h>
#if 0#define int long long
#endifconst int N=5e3+10;
int t,maxp,w;
int ap,bp,as,bs;
int dp[N][N]; //dp[i][j]表示第i天持股j时的最大价值
signed main(){memset(dp,-0x3f,sizeof(dp));std::cin>>t>>maxp>>w; //t天,持股不能超过maxp,交易间隔w天for (int i=1;i<=t;i++){//买入价ap,卖出价bp,最多买入as,最多卖出bsstd::cin>>ap>>bp>>as>>bs; //凭空买入for (int j=0;j<=as;j++){dp[i][j]=-ap*j;}//不买不卖for (int j=0;j<=maxp;j++){dp[i][j]=std::max(dp[i][j],dp[i-1][j]);}if (i<=w){continue;}//买入std::deque<int> deq;for (int j=0;j<=maxp;j++){if (!deq.empty() && deq.front()<j-as){deq.pop_front();}while (!deq.empty() && dp[i-w-1][deq.back()]+deq.back()*ap-j*ap<=dp[i-w-1][j]){deq.pop_back();} deq.push_back(j);dp[i][j]=std::max(dp[i][j],dp[i-w-1][deq.front()]-ap*(j-deq.front()));}deq.clear();//卖出for (int j=maxp;j>=0;j--){if (!deq.empty() && deq.front()>j+bs){deq.pop_front();}while (!deq.empty() && dp[i-w-1][deq.back()]+deq.back()*bp-j*bp<=dp[i-w-1][j]){deq.pop_back();}deq.push_back(j);dp[i][j]=std::max(dp[i][j],dp[i-w-1][deq.front()]+bp*(deq.front()-j));}}std::cout<<dp[t][0];return 0;
}
相关文章:

单调队列优化dp
文章目录 单调队列优化dp烽火传递修剪草坪绿色通道琪露诺旅行问题Watching Fireworks is Fun瑰丽华尔兹股票交易 单调队列优化dp 文章首发于我的个人博客:欢迎大佬们来逛逛 单调队列优化dp的建模形式:这是窗口右滑动的情况 对于窗口左滑动的也是同理。…...

【低压配电漏电继电器660V/LLJ-100H/AC220V 中性点漏电保护 JOSEF】
LLJ-F(S)系列漏电继电器 系列型号: LLJ-10F(S)漏电继电器LLJ-15F(S)漏电继电器LLJ-16F(S)漏电继电器 LLJ-25F(S)漏电继电器LLJ-30F(S)漏电继电器LLJ-32F(S)漏电继电器 LLJ-60F(S)漏电继电器LLJ-63F(S)漏电继电器LLJ-80F(S)漏电继电器 LLJ-100F(S)漏电继电器LLJ-120…...

[数据结构习题]栈——中心对称链
[数据结构习题]栈——中心对称链 👉知识点导航💎:【数据结构】栈和队列 👉[王道数据结构]习题导航💎: p a g e 70.4 page70.4 page70.4 本节为栈和链表综合练习题 题目描述: 🎇思路…...

AMD Software Adrenalin Edition 23.5.1驱动发布,快速获取驱动
AMD新驱动赶在五月天发布!AMD Software Adrenalin Edition 23.5.1驱动 ,为部分游戏带来支持,以及为重要的软件带来修复。驱动人生带大家一览AMD WHQL 23.5.1驱动的优化内容。 游戏方面,AMD WHQL 23.5.1主要为游戏《指环王&#x…...

Visual Studio内引用Lua解释器,编译Lua源码,执行Lua脚本
前言 本篇在讲什么 在Visual Studio中引入lua的解释器 使用C调用Lua文件 本篇适合什么 适合初学Lua的小白 适合需要C/C和lua结合开发的人 本篇需要什么 对Lua语法有简单认知 对C/C语法有简单认知 依赖Lua5.1的环境 依赖VS 2017编辑器 本篇的特色 具有全流程的图文…...

【赏】C语言迷宫游戏设计如何解决屏幕严重刷屏问题同时实现运行时间的显示
要解决屏幕严重刷屏问题,可以参考以下方法: 在每次刷新前清空屏幕,使用system("cls")命令来实现清屏。 只在需要更新的地方进行刷新,而不是整个屏幕都重新绘制。在此代码中,只需要在用户输入移动指令后更新电子鼠的位置即可,不用每次循环都重新画整个迷宫。同时…...

Spring Boot如何实现接口文档自动生成
Spring Boot如何实现接口文档自动生成 在开发Web应用程序时,接口文档是非常重要的一环,它可以帮助我们快速了解API的功能和使用方法,同时也是与其他开发人员和团队协作的重要工具。然而,手动编写和维护接口文档是一项繁琐的工作&…...
)
二进制概述-0day漏洞利用原理(1)
二进制利用基本原理,Lord PE的使用,凡是资源性的物质且可表达的皆可利用。 往期文章: 漏洞概述-0day漏洞利用原理(0)_luozhonghua2000的博客-CSDN博客 PE 文件格式 PE (Portable Exec utable) 是 Win32 平台下可执行文件遵守的数据格式。常见的可执行文件(如“*.exe”文件…...

加密与解密 调试篇 动态调试技术 (二)-常见断点
目录 常见的断点 1.INT 3 断点 检测 绕过 2.硬件断点 原理 我们给出硬件中断的例子 删除硬件断点 3.内存断点 原理 例子 删除 区别 总结 4.内存访问一次性断点 5.消息断点 例子 删除 6.条件断点 (1)按寄存器条件中断 (2&…...

【JavaScript】拾遗(5.25)
文章目录 1. JavaScript2.HTML嵌入JS的第一种方式:行间事件3.HTML嵌入JS的第二种方式:脚本块的方式4. HTML嵌入JS的第三种方式:外部式(外链式)5. 局部变量和全局变量6. 函数7.事件8.回调函数8.1 注册事件8.2 代码的执行顺序 1. JavaScript JavaScript是一门脚本语言。…...
QMI8658 - 姿态传感器学习笔记 - Ⅲ
文章目录 1.复位1.1 上电复位:1.2 推荐工作条件 2. 校准(COD)2.1 校准步骤2.2 校准注意事项:2.3 校准状态指示2.4 校准参数更新 3. 自检3.1 加速度计自检3.2 陀螺仪自检 4. Ctrl94.1 写Ctrl94.2 读Ctrl94.3 Ctrl9详细命令说明 5. 中断5.1 同步采样模式5.…...
PHP+vue二手车交易信息网站系统
原来二手车网站由于二手车网站制度的不完善,许多城市的二手车网站市场都很少,而且欺诈行文较严重,肆意提高价格,隐瞒汽车所存在的故障问题,人们买卖二手车还是经过朋友帮忙介绍的途径来实现。这就导致了很多人的想卖车…...

NTM中attr的用法
代码1 attrs class CopyTaskParams(object):name attrib(default"copy-task")controller_size attrib(default100, convertint)controller_layers attrib(default1,convertint)num_heads attrib(default1, convertint)sequence_width attrib(default8, convert…...
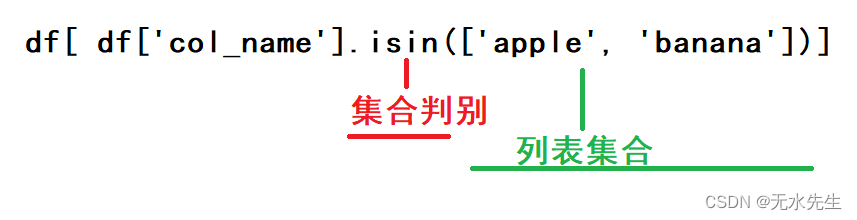
【python资料】pandas的条件查询
一、说明 在使用Pandas的DataFrame进行数据挖掘的时候,需要形形色色的条件查询,但是这些查询的基本语法是啥,查询的灵活性如何,本文将对他们进行详细列出,便于以后查阅。 二、Pandas条件查询方法 2.1 简单条件查询 1、…...
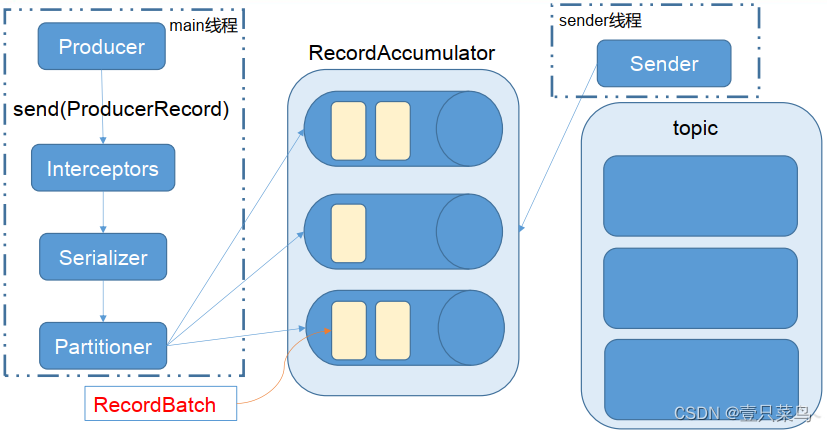
中间件(三)- Kafka(二)
Kafka 6. 高效读写&Zookeeper作用6.1 Kafka的高效读写6.2 Kafka中zookeeper的作用 7. 事务7.1 Producer事务7.2 Consumer事务 8. API生产者流程9. 通过python调用kafka9.1 安装插件9.2 生产者(Producer)与消费者(Consumer)9.3…...
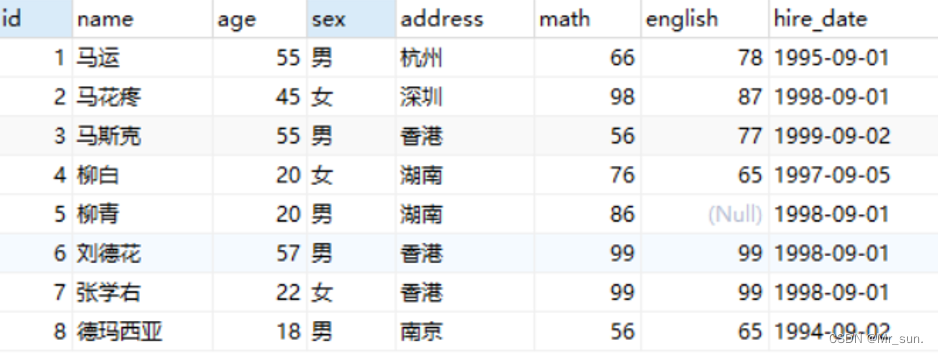
DAY01_MySQL基础数据类型navicat使用DDL\DML\DQL语句练习
目录 1 数据库相关概念1.1 数据库1.2 数据库管理系统1.3 常见的数据库管理系统1.4 SQL 2 MySQL2.1 MySQL安装2.1.1 安装步骤 2.2 MySQL配置2.2.1 添加环境变量2.2.2 MySQL登录2.2.3 退出MySQL 2.3 MySQL数据模型2.4 MySQL目录结构2.5 MySQL一些命令2.5.1 修改默认账户密码2.5.2…...
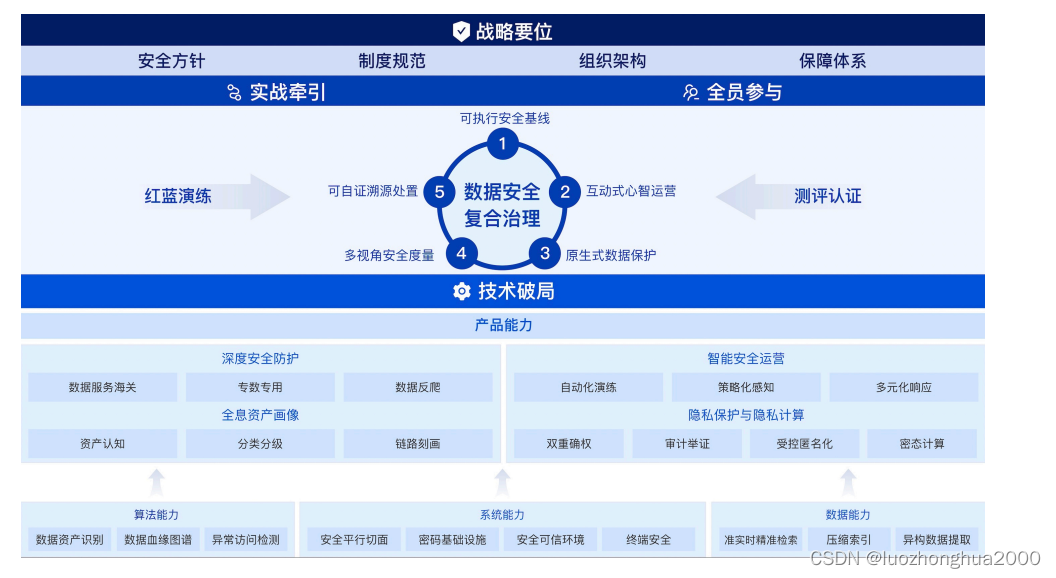
数据安全复合治理框架和模型解读(0)
数据治理,数据安全治理行业在发展,在实践,所以很多东西是实践出来的,哪有什么神仙理论指导,即使有也是一家之说,但为了提高企业投产比,必要的认知是必须的,当前和未来更需要专业和创新。数据安全治理要充分考虑现实数据场景,强化业务安全与数据安全治理,统一来治理,…...

Java程序设计入门教程--逻辑运算符和位运算符
目录 逻辑运算符 位运算符 逻辑运算符 逻辑运算符就是表示逻辑关系的运算符。下表列出了逻辑运算符的基本运算,假设布尔变量A为真,变量B为假。 逻辑运算符表 操作符 描述 例子 && 当且仅当两个操作数都为真,条件才为真。 &…...
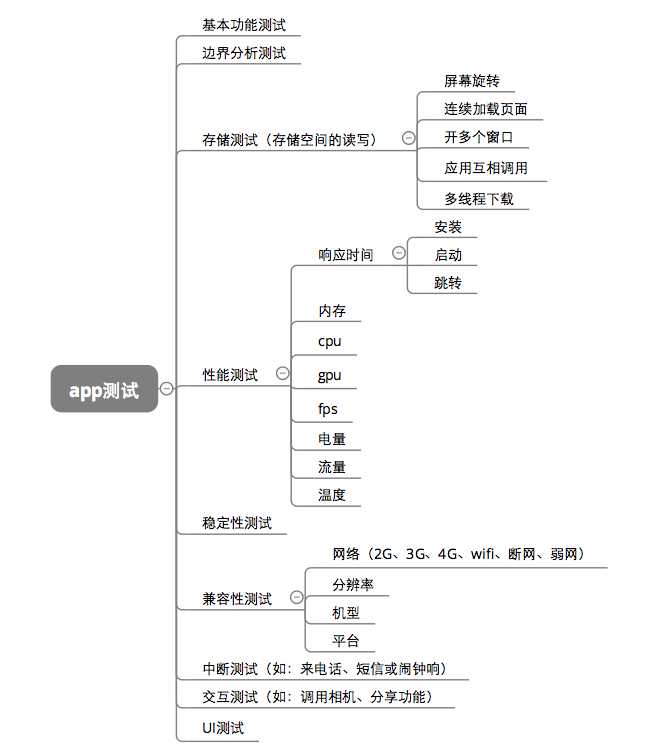
接口测试简介以及接口测试用例设计思路
接口测试简介 1.什么是接口 接口就是内部模块对模块,外部系统对其他服务提供的一种可调用或者连接的能力的标准,就好比usb接口,他是系统向外接提供的一种用于物理数据传输的一个接口,当然仅仅是一个接口是不能进行传输的&#x…...

C++ Qt项目实战:构建高效的代码管理器
C Qt项目实战:构建高效的代码管理器 一、项目概述(Introduction)1.1 项目背景(Project Background)1.2 项目目标(Project Goals)1.3 项目应用场景(Project Application Scenarios&am…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
